峡谷河流的挂网式人行悬索桥设计

李 兵，王国华，王天宇，陈若飞

（1.江苏交通工程咨询监理有限公司，江苏 南京 211800；2.东南大学土木工程学院，江苏 南京 211189）

0 引言

目前，峡谷河流景区人行悬索桥通常采用传统的平行缆索体系悬索桥结构形式。峡谷河流景区人行悬索桥采用高大的桥塔、锚碇结构和吊索体系，必定导致其经济性指标较高[1-3]。

峡谷河流景区人行悬索桥的桥面狭窄，结构轻盈，因此，其抗侧刚度和抗扭刚度低，颤振抗风稳定性较差[4-7]。

如何利用峡谷河流景区的地形地貌，建造适合峡谷河流景区特色的人行悬索桥，是工程师面临的难题[8-10]。

借鉴悬挂式蜘蛛网的结构原理，针对峡谷河流景区人行悬索桥，本文提出一种峡谷河流的悬崖陡壁挂网式人行悬索桥结构。该桥采用双曲抛物面空间缆索网分散锚固于峡谷河流景区两侧的悬崖陡壁岩石之上，取消桥塔结构和锚碇结构，也取消吊索体系，从而节约了造价，且施工简便，同时空间缆索网又提高了悬索桥的抗侧刚度和抗扭刚度，加强了其抗风稳定性。

本文结合某150 m跨径的峡谷河流人行景观悬索桥设计，对所提出的挂网式双曲抛物面空间缆索网人行悬索桥的构型进行研究，并通过建立的Midas有限元分析模型，进行内力分析计算，开展动力模态分析研究，以验证挂网式双曲抛物面空间缆索人行悬索桥的优越性。

1 构型研究

双曲抛物面俗称马鞍双曲面，是一种经典的二次直纹曲面（见图1）。它由2族空间交叉的直线构成曲面，其数学方程为：

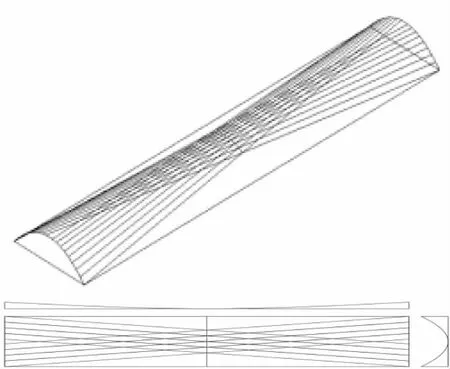
图1 马鞍双曲面

式中：fx、fy别为双曲抛物面索网纵向矢高和横向矢高；a、b分别为半长和半宽。

马鞍双曲面的2族直线水平投影为平行线，其直纹线水平投影的斜率K为：

针对峡谷河流人行悬索桥，所提出的挂网式双曲抛物面空间缆索网人行悬索桥包括：双曲抛物面空间缆索网体系、悬崖陡壁锚固基础梁、岩石锚索和管桁架式桥面加劲梁。双曲抛物面空间缆索网体系是由数根工厂预制的成品缆索空间交叉构成，其空间几何构型为槽口向上的双曲抛物面空间缆索网下垂形成的凹口状空间缆索网，双曲抛物面空间缆索网分散锚固在峡谷两侧的悬崖陡壁锚固基础梁之上，悬崖陡壁锚固基础梁的背部则设置一定数量的岩石锚索（见图2）。

图2 挂网式空间缆索人行悬索桥

双曲抛物面空间缆索由多股缆索交叉布置，空间缆索网提供水平分力，具有良好的抗侧刚度，避免了峡谷河流景区人行悬索桥的左右摇摆晃动；且空间缆索网的空间整体性好，能大幅度提高人行悬索桥的抗扭刚度，从而大幅度提高其抗风稳定性。

双曲抛物面空间缆索分散锚固于峡谷河流景区两岸的悬崖陡壁之上，悬崖陡壁替代了桥塔结构，因而人行悬索桥没有一个桥塔结构，可以大幅度降低造价。

双曲抛物面空间缆索网由细小直径的多股缆索组成，而小直径的多股缆索可以采用工厂预制的缆索成品，直接悬挂在两岸的悬崖陡壁之上，再用分散的岩石锚索群锚固，不需要临时猫道，不需要修建大型锚碇基础，装配式施工快捷简便。

挂网式双曲抛物面空间缆索人行悬索桥是平拉式悬索桥，没有吊索，底部抛物线形的管桁架式桥面系加劲梁直接搁置在槽口向上双曲抛物面的空间缆索网兜之上，施工同样简便（见图3）。

图3 管桁架式桥面系加劲梁

挂网式双曲抛物面空间缆索人行悬索桥采用槽口状双曲抛物面空间缆索网，曲线优美，造型独特，结构轻盈（见图4）。

图4 峡谷河流挂网式悬索桥的效果图

2 设计参数

某峡谷河流景区人行悬索桥主跨径为150 m，玻璃桥面宽度7 m。为了降低造价，取消桥塔结构，取消吊索，采用挂网式双曲抛物面空间缆索人行悬索桥的结构方案，槽口状双曲抛物面空间缆索网分散锚固在峡谷两侧的悬崖陡壁之上（见图5）。

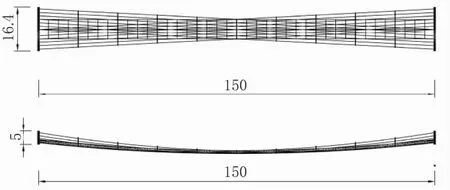
图5 总体设计图（单位：m）

双曲抛物面索网的几何尺寸为：长度150 m，两端宽度15 m，中间宽度7.5 m，长度方向的矢高0.937 5 m，在两端处宽度方向的矢高3.75 m；2组直纹线的平面投影斜率K为0.05。

双曲抛物面索网的下垂矢跨比为1/30，在桥跨中间下垂5 m，是一种平拉式空间缆索网人行悬索桥；双曲抛物面索网采用14根直径45 mm的2 000 MPa高强钢丝，形成双曲抛物面交叉索网悬索结构体系。

在悬崖陡壁锚固基础梁的背部设置一定数量的岩石预应力锚索，岩石预应力锚索采用双排布置。岩石预应力锚索长度为30 m，锚索间距为0.5 m，锚索直径为25 mm，采用强度为18 600 MPa的预应力钢绞线制作；在人行悬索桥的单侧设置56根，全桥共布置112根岩石预应力锚索。

悬崖陡壁锚固基础梁采用抛物线弧形的钢筋混凝土基础梁，抛物线形的钢筋混凝土基础梁长度为17 m，梁高为1.2 m，梁厚度为0.8 m，梁内部配置钢筋。

抛物线形的钢结构曲梁搁置在双曲抛物面空间缆索网兜之上，间距为15 m，采用直径375 mm空心钢管，钢管壁厚12 mm。

管桁架式桥面加劲梁由弧形桁架、纵向系杆和纵向桁架式支撑组成，在管桁架加劲梁的顶面安装玻璃桥面板。

弧形桁架由抛物线弧形下弦杆、水平上弦杆和竖杆构成，且均采用直径200 mm空心钢管制作，钢管壁厚6 mm。

左右2根纵向系杆连接多片弧形桁架的两边端部，纵向系杆采用直径180 mm空心钢管制作，钢管壁厚5 mm。

纵向桁架式支撑的下弦杆和上弦杆采用直径180 mm空心钢管制作，钢管壁厚4 mm；纵向桁架式支撑的腹杆采用直径100 mm空心钢管制作，钢管壁厚3 mm。

桥面板采用厚40 mm的钢化玻璃，玻璃桥面板搁置在管桁架加劲梁的顶面（见图6），游客行走在玻璃桥面之上，头顶白云，脚下滚滚江水波涛汹涌，大峡谷葱葱郁郁，生机盎然，曲径幽深，妙趣横生。

图6 挂网式人行悬索桥的玻璃桥面

3 受力性能分析

3.1 有限元建模

本设计采用Midas软件建模，双曲抛物面空间缆索网采用索单元，抛物线形的钢结构曲梁和管桁架桥面加劲梁采用梁单元。Midas有限元模型见图7。

图7 Mida s有限元模型

按照零位移原则，找形得到主缆的初始应力状态后，通过反复修正，使成桥状态的有关控制参数满足要求，从而获得主缆的成桥线形。

3.2 竖向荷载作用下的计算结果

对主跨桥面做满荷加载，桥面附加恒荷载采用均布荷载标准值7 kN/m2，桥面活荷载采用均布荷载标准值5 kN/m2。

竖向荷载作用下计算结果（恒+活）见图8。

图8 竖向荷载作用下计算结果（恒+活）

活荷载作用下最大竖向位移出现在跨中位置，最大位移为178.8 mm。依据《景区人行玻璃悬索桥与玻璃栈道技术标准》（DB13（J）/T 264—2018），该位移满足规范规定的1/500限值要求。主缆最大内力为4 150.6 kN，主缆最大应力为682.4 MPa，满足承载能力要求。管桁架桥面加劲梁最大应力为196.7 MPa，钢材选用Q355钢材，可以满足承载能力要求。

3.3 动力模态计算结果

为了不遗漏任何振型，分析过程中采用子分块法求解特征方程，本工程典型的振型见图9。

图9 动力模态

由图9可知：（1）第1阶振型为反对称竖弯，频率为0.566 Hz；第2阶振型为正对称竖弯，频率为0.802 Hz，竖向振动频率较高，表明本桥竖向刚度较大。（2）第3阶振型为正对称侧弯，频率为较高的0.815 Hz，先出现竖弯振型，然后是侧弯振型。分析表明，双曲抛物面空间交叉缆索网提供水平分力，大幅度提高了悬索桥的抗侧刚度，可避免其出现侧向摇摆问题。（3）直到第13阶才出现正对称扭转振型，先发生正对称扭转振动，频率为较高的2.588 Hz，后发生反对称扭转振动，频率为2.883 Hz。分析表明，双曲抛物面空间交叉缆索网和管桁架桥面加劲梁两者协同工作，可大幅度提高悬索桥的抗扭刚度，扭弯频率比值为4.57，较高，说明该桥具有良好的抗风稳定性。

3.4 颤振临界风速

横断面非流线型的悬索桥通常采用分离流扭转的颤振临界风速计算中的Selberg公式来分析悬索桥的颤振稳定性。

Selberg公式为：

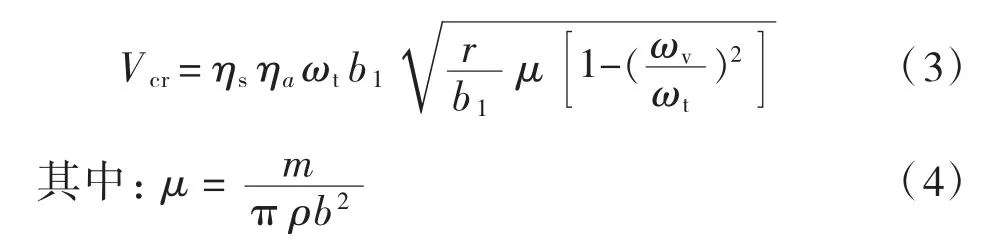
式中：Vcr为颤振临界风速；ηs为主梁截面形状影响系数；ηɑ为攻角效应系数；r是桥梁断面（包括加劲梁和主缆）惯性半径；b1为加劲梁截面的半桥宽；μ为桥梁与空气的密度比；m为加劲梁及主缆的质量密度；ρ为空气密度；ωt、ωv分别为最低阶扭转圆频率和竖向圆频率；b为加劲梁截面的桥宽，b=2b1。

本设计中，ηs、ηα均取1.0；经过计算，r=4.74 m，μ=2.06，ωt、ωv分别为16.26 rad/s、3.56 rad/s。因此，本设计的颤振临界风速为：

通过以上计算可知，该桥的颤振临界风速较高，说明本设计具有较好的抗风稳定性。

4 结 语

（1）双曲抛物面空间缆索网分散锚固于峡谷河流两侧的悬崖陡壁岩石之上，取消了桥塔和吊索体系，因而节约了造价，且施工简便。

（2）双曲抛物面空间交叉缆索网提供水平分力，大幅度提高了悬索桥的抗侧刚度，先出现竖弯振型，然后是侧弯振型，且侧向振型的频率较高。抗侧刚度较大时，可避免出现悬索桥的侧向摆动问题。

（3）槽口向上的双曲抛物面空间缆索网和底部抛物线形的管桁架桥面加劲梁两者协同工作，大幅度提高了挂网式双曲抛物面空间缆索人行悬索桥的抗扭刚度，扭弯频率比值较高，因此，该桥具有良好的抗风稳定性。