井下节流气井井底压力计算方法应用研究
2022-09-23张凌筱
张凌筱
(中国石油化工股份有限公司 华北油气分公司,河南 郑州 450006)
准确计算带井下节流装置的产水气井井底压力,是预测气井产能、制定合理排水采气制度的重要基础。目前产水气井的井底压力主要靠压力计和回声仪测试得到[1]。井下节流气井受节流装置影响,井筒不通畅,常规压力计难以下至油管底部位置,井底压力测试困难。回声仪测试用于气井时也存在难题,受气体影响,气液界面非常模糊,导致液面确定不准确,会影响气层中部深度压力的计算。因此,本文建立了一套井下节流气井井底流压计算方法,并与井下节流气井全井筒多位置多点流压测试结果进行对比评价。
1 井下节流气井全井筒压力预测方法
1.1 气液两相管流压降模型优选
井下节流气井全井筒压降包括管流压降和嘴流压降两大部分。目前常用产水气井气液两相管流压降模型[2-6]包括Hagedorn-Brown、Beggs-Brill、Mukherjee-Brill、Gray和NoSlip[7]等5种模型。
以东胜气田X井为例,该井目的层H2,完钻井身3 246.31 m,水平段长为861.31 m,造斜点深度为1 761.4 m(垂深1 760.64 m)。气体相对密度为0.605,生产油管内径为62 mm,油管下深为2 369.68 m,A点斜深为2 385.00 m(垂深为2 146.92 m)。5次流压测试期间气井的生产数据及测试结果分别见表1、表2。

表1 锦26井流压测试期间的生产数据表

表2 锦26井盒2气层测试流压数据表
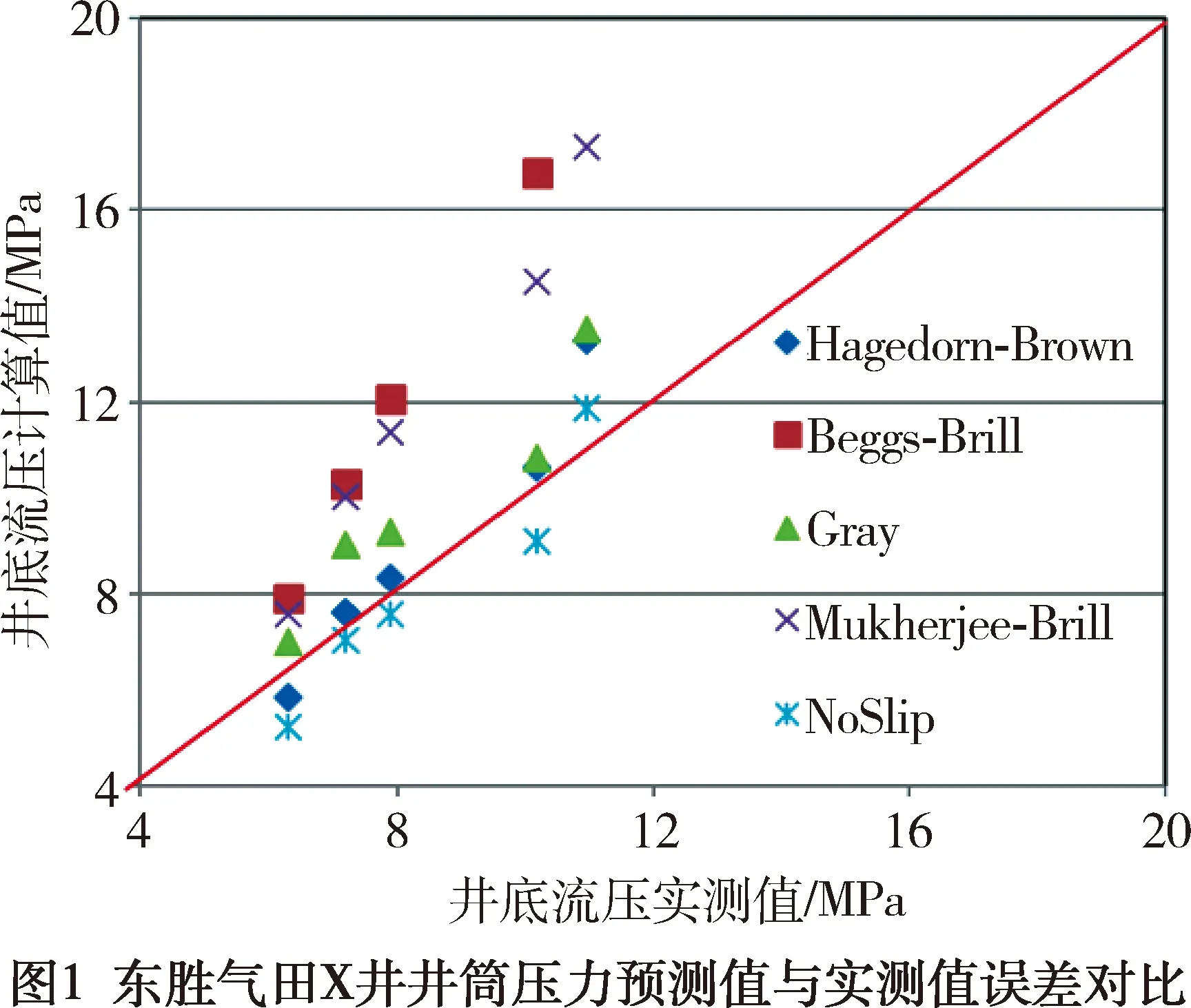
通过现场实测流压数据(见图1)评价[8],No-Slip模型计算的压力值与测试值较接近,散点均匀分布在中心线两侧,平均压降百分误差为-5.01%,平均绝对压降百分误差为8.34%,标准差为5.76%(见表3),准确性最好。其次为Hagedorn-Brown模型,这两种模型均明显优于其它模型,因而东胜气田产水气井可选用No-Slip或Hagedorn-Brown模型预测井筒管流压降变化规律。

表3 锦26井压力预测值与实测值的误差对比
1.2 气液两相嘴流压降模型建立
目前产水气井气液两相嘴流嘴流压降计算方法有Gilbert三参数和Gilbert四参数关系式、Omana无因次关系式等经验模型,这类经验模型适用条件有限,预测结果差异较大;Ashford模型[9]、Sachdeva模型、Perkins模型等机理模型精度较高,但是计算工作量大,工程应用推广难度大。因此,有必要优化建立一个适合气液两相嘴流压降模型,同时满足工程精度和现场生产要求。
1.2.1 物理模型及基本假设
物理模型如图2所示,嘴流可简化为两个控制体,第一个控制体起始于位置①,结束于位置②,代表突缩件;第二个控制体起始于位置②,结束于位置③,代表突扩件。①代表嘴流上游位置;②代表嘴流喉部位置;③代表嘴流下游位置,压力恢复点;“B”代表嘴流出口位置。模型推导过程中,做了以下基本假设:

1)流动为一维流动;
2)气液之间分相独立流动,存在相间滑脱;
3)忽略液相的压缩性,气相多变膨胀[5];
4)整个嘴流过程,滑脱因子为一常数;
5)流动过程无相间变化,气体的质量分数不变。
1.2.2 基本定义
气液混合物流过节流件时压力降低,气体膨胀,气体流速大于液体,气液间产生滑脱。嘴流过程通常用滑脱因子描述气液之间的流速比关系。滑脱因子K定义为
(1)
式中,u为速度,m/s;K为滑脱因子,无因次量;下标G、L分别表示气相和液相。
考虑滑脱的气流、液流平均速度及混合物动量通量分别见式(2)、(3)、(4)。
(2)
(3)
(4)
式中,x为气体质量分数;α为空隙率;M为质量流量,kg/s;A为流体流动截面积,m2;v为流体比容,m3/kg;G为混合物质量通量,kg/(s·m2);MF为动量通量,Pa;下标G、L分别表示气相和液相。
将式(2)、式(3)代入式(4)中,导出存在滑脱时混合物动量通量
(5)
由于存在滑脱时等效动量比容为:
(6)
因此,得到存在滑脱时等效速度
ue=Gve
(7)
1.2.3 气液两相嘴流压降模型
对于第一个控制体,起始于位置①,结束于位置②,由力平衡原理得到:
-Adp=Mdue
(8)
将式(7)代入式(8)中,并积分得到:
(9)
式中,下标1、2分别代表截面位置处对应参数值。
由于A1≫A2,ue2≫ue1,故忽略ue1,积分式(9)可简化为:
(10)
(11)
式中,A1为油嘴上游管段过流面积,m2;Ac为油嘴喉部有效过流面积(Ac=A1Ccσ),m2;Cc为收缩系数;σ为过流面积之比(σ=Ac/A1)。
流体经节流后,再流过控制体二的突扩件时,压力得到一定程度恢复。对于第二个控制体,起始于位置②,结束于位置③,由力平衡原理知
(12)
式中,A3为油嘴下游管段过流面积,m2;
由嘴流特性和压力波传播理论知,当嘴流流态为临界流时,油嘴喉部压力P2与油嘴出口压力PB不为一个压力体系,即P2≠PB,PB为自由变量。当流动条件为亚临界流时,油嘴喉部压力P2与油嘴出口压力PB为一个压力体系,即P2=PB。
根据式(12)可得到恢复压力为
(13)
式(10)和式(13)是两相嘴流压降模型的核心关系式。根据式(10)和式(13)可计算出两相流体通过不同嘴径时的节流压降,为井下节流气井井底流压计算奠定了基础。
通过对井下节流气井节流器前后放置压力计进行长期动态监测[10-12],评价该模型应用在高液气比气井中具有较好的准确性(见图3),误差为6.23%,可满足井下节流器嘴径设计精度要求。

1.3 井下节流气井全井筒压力计算方法
采用气液两相嘴流模型、井筒两相管流模型相结合的方式,综合预测井下节流过程压力等动态参数变化规律[13-15]。基本步骤为:
1)假设节流器上部管段积液,液面距节流器高度H1;
2)采用气液两相管流模型(No-Slip或Hagedorn-Brown模型)预测从井口到液面位置油管压力;
3)根据液面位置油管压力和液面高度,确定节流器出口压力;
4)根据节流器出口压力,采用周舰节流压降模型计算节流器入口压力;
5)以节流器入口压力为初值,再次采用气液两相管流模型(No-Slip或Hagedorn-Brown模型)计算从节流器至井底压力Pwf1;
6)不考虑油套环空积液影响,根据气井套压折算井底流压值Pwf2;
7)当Pwf1=Pwf2,认为假设的液面高度与实际较为一致,从而确定井下节流气井井底流压值为Pwf1;否则重新调整液面高度,通过反复迭代确定合理液面高度和井底流压值。
2 井下节流气井全井筒压力预测方法评价
为评价本文的井下节流气井全井筒压力预测方法的准确性,创新性地在东胜气田JPH-334和JPH-343两口不积液或微积液气井开展多点流压测试试验进行数据评价,即JPH-343井在节流器下部965 m、节流器下部840 m、节流器下部712 m、节流器下部13 m、节流器上部15 m共5个位置,下放安装存储式压力计;JPH-334井在节流器下部916 m、节流器下部504 m、节流器下部28 m、节流器上部17 m共4个位置,下放安装存储式压力计对流体压力和温度进行长期监测,其基础参数见表4所示,其测试参数见表5所示。
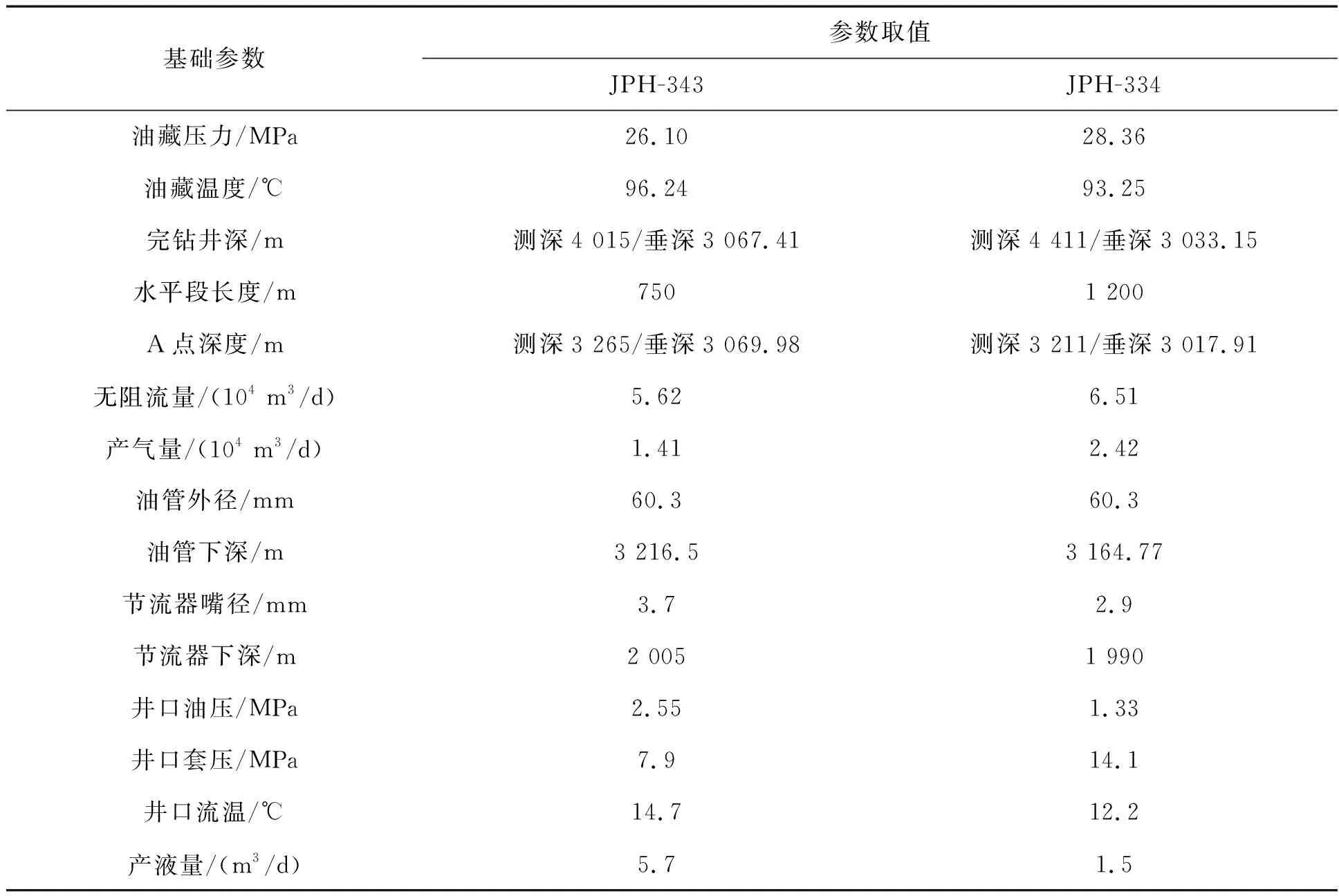
表4 气井基础参数
利用表4基础参数,采用本文方法对节流器前、后的井筒压力参数进行预测,并与表5中实测的流压数据进行对比,如图4和图5所示。两口井下节流气井井筒压力预测值与实测值平均误差仅为2.87%,表明井下节流气井井筒压力预测模型具有较好的准确性,满足工程计算精度要求。JPH-334井从油管预测井底流压值17.2 MPa,与从套管折算的井底流压16.6 MPa相差0.6 MPa,误差仅为3.6%;JPH-343井从油管预测井底流压9.9 MPa,与从套管折算的井底流压9.6 MPa,相差0.3 MPa,流压实测值与预测值平均误差仅为3.0%,本文方法可以用于井下节流气井井底流压计算。
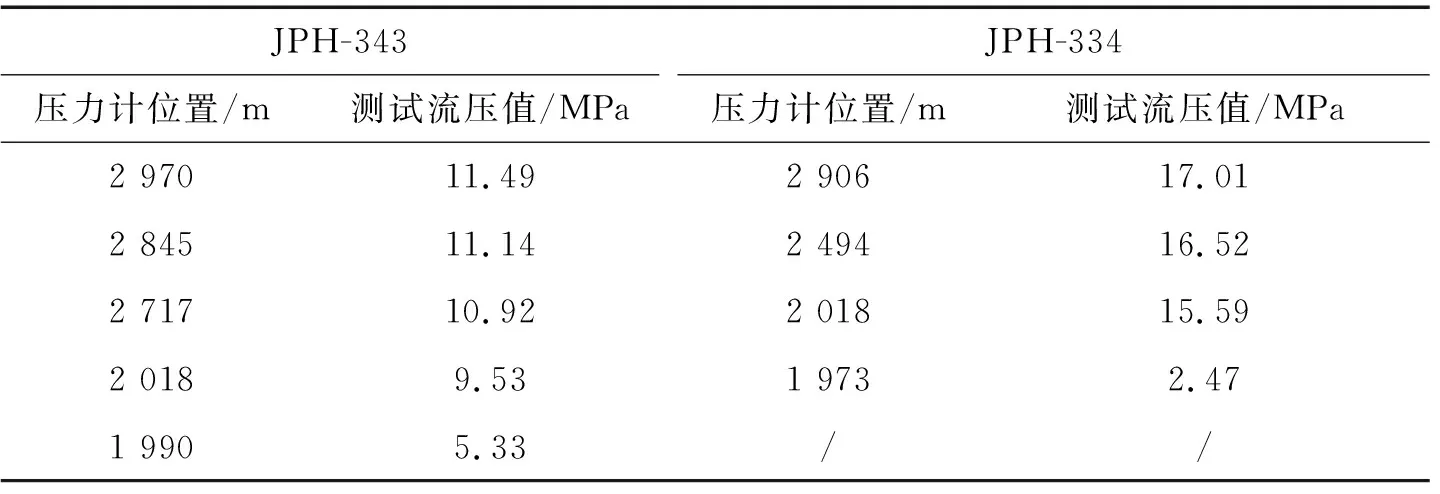
表5 多点流压测试井流压实测数据


3 结论
1)利用东胜气田多井次现场实测流压数据评价5种气液两相管流压降模型,发现No-Slip模型计算的压力值与测试值较接近,平均压降百分误差为-5.01%,平均绝对压降百分误差为8.34%,标准差为5.76%,准确性最好,可用来预测东胜气田气井井筒管流压降变化规律。
2)引入滑脱因子K表征气液两相间滑脱效应,建立了气液两相嘴流压降模型,评价表明,新模型预测节流器入口压力与实测值较接近,误差仅为6.23%,满足工程计算精度要求。
3)基于气液两相嘴流压降模型与No-Slip/H-B管流压降模型全井筒耦合,优化建立井下节流气井全井筒压力预测方法。评价表明,气井井底压力预测值与实测值平均误差为2.87%,可用于气井全井筒积液高度和井底流压值实时定量预测,为类似气藏低压集输开发模式下精细开发和长期稳产提供技术借鉴和指导意义。
