一个函数值求解问题中的斐波那契数列及其推广

◎卢予奇 卢兴江

(1.浙江省富阳中学，浙江 杭州 311499；2.浙江大学数学科学学院，浙江 杭州 310027)

数学问题蕴藏在生活的各个角落，有心者常常会在不经意间捕捉到身边与数学相关的细节笔者在观看某教育题材电视连续剧时，就特别留意了剧中数学老师布置给同学的一道每日难题，从近景镜头中能看到黑板上题目的全貌为便于本文叙述，现将这道题目的文字表达做些许改动，表述如下：

已知(),()为定义在正整数集上的函数，()为严格单调增加函数，其函数值亦为正整数，而()=[()]+1,∈

记集合,分别为(),()的值域，即={(1),(2),(3),…},={(1),(2),(3),…}，若∪=,∩=∅，试求(240)的值

剧中插班生稍加思索，就在黑板上奋笔疾书，他根据不完全归纳法寻找(),()函数值的规律，得到了答案389

笔者出于对数学的兴趣，对该题进行了求解，对问题背后的数学原理进行了研究

首先计算出(),()的前若干项，初步观察数字规律根据题设条件，(),()的值域互不相交，且覆盖了整个正整数集，又因为()是严格单调增加的，所以()也是严格单调增加的

由(1)<(2)<(3)<…且()=[()]+1>[()],知(1)=1,(1)=[(1)]+1=(1)+1=2

由(),()的单调性，必有()≥+1,()=[()]+1≥()+2≥+3,=2,3,4,…

因为(2)≥5，所以(2)=3,(3)=4,(2)=[(2)]+1=(3)+1=5

因为(3)=[(3)]+1=(4)+1>(4)，所以(4)=6,(3)=[(3)]+1=(4)+1=7

依次类推，可以计算出(),()前若干项的取值，见表1，若采用计算机C语言编程，可以更快速地得到(),() 前若干项的取值在程序运行结果中，(240)=388，这表明剧中插班生的计算结果有误，出现错误是因为不完全归纳法只是根据部分研究对象猜想普遍规律，没有严谨的理论推理做支撑

表1 u(x),v(x)前若干项取值

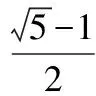
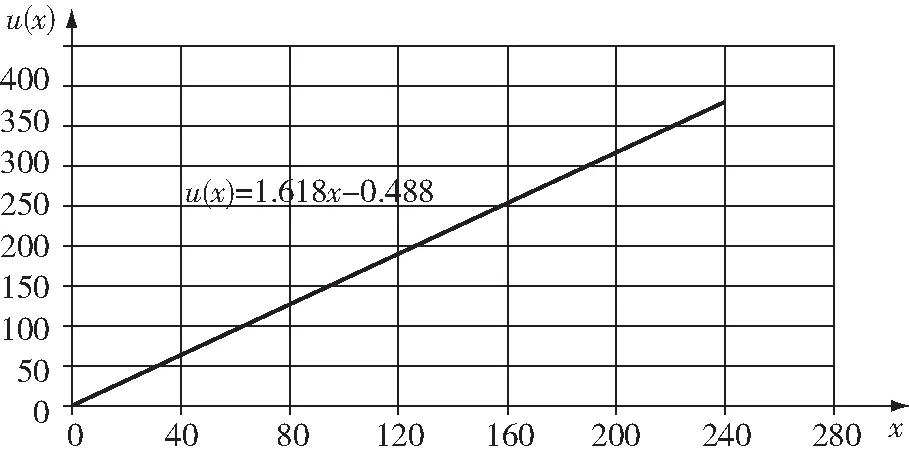
图1 u(x)的经验回归直线

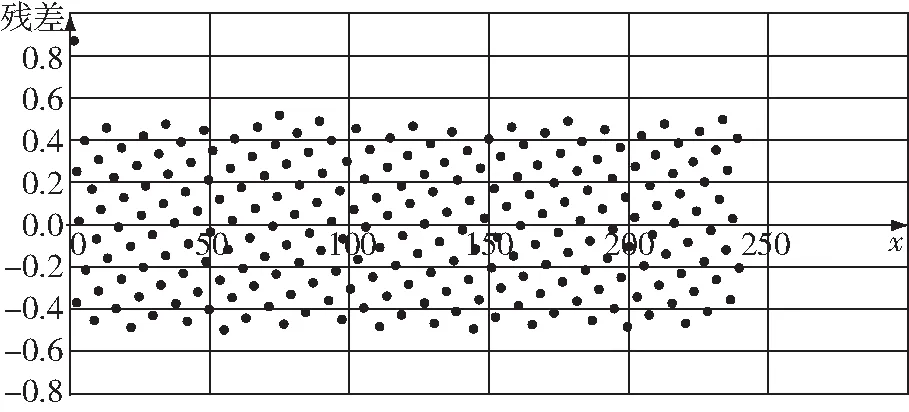
图2 u(x)经验回归直线的残差图

基于这个现象回过头来观察表1，可以发现函数(),()的对应规律中也隐含着斐波那契数列的特征：前3个正整数对应了2个()的函数值和1个()的函数值；前5个正整数对应了3个()的函数值和2个()的函数值；前8个正整数对应了5个()的函数值和3个()的函数值；前13个正整数对应了8个()的函数值和5个()的函数值，涉及的(),()函数值的个数均为斐波那契数列某一项的取值

由此可以猜测以下结论，并采用数学归纳法进行严格证明

设斐波那契数列为{}，满足==1,=-1+-2,=1,2,3,…，则在任意前(≥3)个正整数1,2,3,…,中恰有-1个的元素[即()的函数值]和-2个的元素[即()的函数值]

由表1可知，对=3,4,5,6,7皆成立

假设对=≥3成立，即前个正整数1,2,3,…,中有-1个的元素[即()的函数值]和-2个的元素[即()的函数值]，有

{1,2,3,…,}={(1),(2),…,(-1)}∪{(1),(2),…,(-2)}

由()的单调性可知，集合{(1),(2),…,()}中个元素恰是-1个[()](=1,2,3,…,-1)和-2个[()](=1,2,3,…,-2)所组成的，即有{(1),(2),…,()}={[(1)],[(2)],…,[(-1)]}∪{[(1)],[(2)],…,[(-2)]}

因为()=[()]+1,=1,2,3,…,-1，所以集合{(1),(2),…,(-1)}中各元素分别是集合{[(1)],[(2)],…,[(-1)]}相应元素之后的相邻整数，

所以{1,2,3,…,+1}={[(1)],[(2)],…,[(-1)],[(1)],[(2)],…,[(-2)]}∪{(1),(2),…,(-1)}

即前+1个正整数中有个的元素[即()的函数值]和-1个的元素[即()的函数值]于是结论对=+1亦成立，证毕

(),()的取值其实定义了一种对应规则，所以，当前面个正整数对应了-1个()的函数值和-2个() 的函数值之后，从+1个正整数开始可以看作对应的重新开始，即相当于把正整数+1 替代 1 的位置进行同样的对应，于是可以得到以下推论

对任意的正整数≥3，在数列+1,+2,+3,…前(≥3)项中有-1个的元素[()的函数值]和-2个的元素[()的函数值]

根据结论一与推论一，即可在不采用计算机程序辅助的情况下，计算得到(240)的值

因为=377，所以前377个正整数中有=233个()的函数值和=144个()的函数值

因为=13，所以从+1=378开始的前13个数378，379，380,…,390中有=8个()的函数值和=5个()的函数值

(240)是以上8个()的函数值中第240-233=7个，由表1可知，(7)=11，所以(240)=377+11=388

上述结论一与推论一都是基于题设条件()=[()]+1,∈得到的，若将(),()的关系式改成()=[()]+2，()=[()]+3,∈,情形又会发生怎样的变化？

已知(),()为定义在正整数集上的函数，()为严格单调增加，其函数值亦为正整数，且()=[()]+,∈，其中正整数为常数试确定集合={(1),(2),(3),…},={(1),(2),(3),…}，使其满足∪=,∩=∅

根据题设条件，显然对任意的∈，

有()=[()]+

(1)=1⟹(1)=1+⟹(2)=2,(3)=3,…,()=，

从而有(2)=2+,(3)=3+,…,()=+=2

因为(+1)=[(+1)]+=(2+1)+>3+=4，

所以(+1)=2+1,(+2)=2+2,…,(2)=3；(2+1)=3+1,(2+2)=3+2,…,(3)=4

从而有(+1)=4+1,(+2)=4+2,…,(2)=4+=5，依次类推

事实上，将条件()=[()]+1,∈下所得结果中每个()或()的位置依次用连续的个()或()去对应即可

比如表2列出了当=3时(),()前若干项的取值，由此可得到以下结论和推论

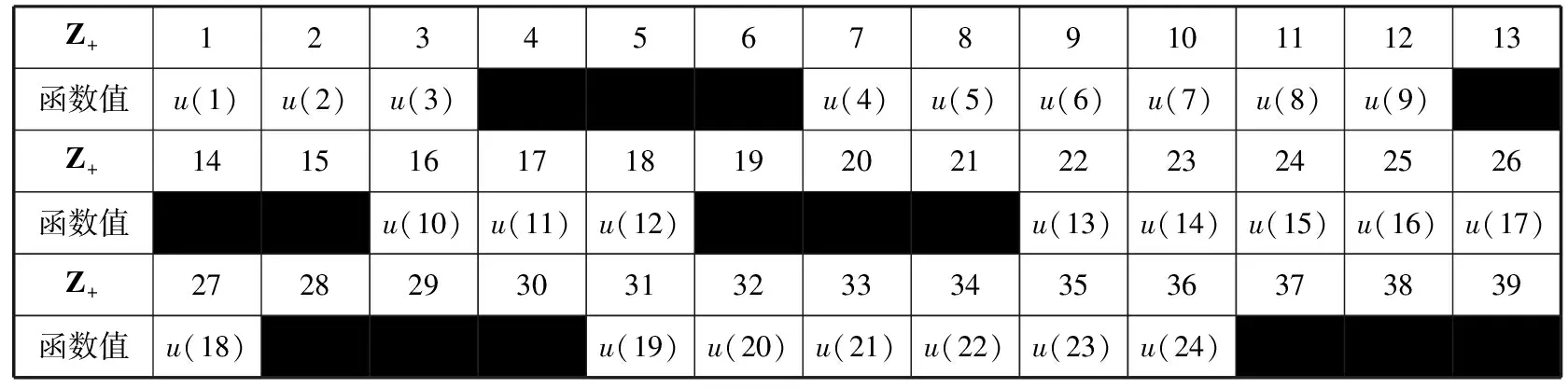
表2 推广形式一：u(x),v(x)前若干项的取值

设斐波那契数列为{}，对()=[()]+,∈的情形有：在任意前(≥3)个正整数1,2,3,…,中，恰有-1个的元素[即()的函数值]和-2个的元素[即()的函数值]

对()=[()]+,∈的情形，对任意的正整数和正整数≥3，数列+1,+2,+3,…中前(≥3)项有-1个的元素[即()的函数值]和-2个的元素[即()的函数值]

在上述推广形式中，()与[()]间的差值是一个常数若将问题进一步推广，将(),()的关系式改成()=[()]+,∈,情形就会变得更复杂，此时是否还具有斐波那契数列的特征？

已知(),()为定义在正整数集上的函数，()为严格单调增加函数，其函数值亦为正整数，且()=[()]+,∈，试确定集合={(1),(2),(3),…},={(1),(2),(3),…}，使其满足∪=,∩=∅

因为()=[()]+,=1,2,3,…，所以在正整数列1,2,3,4,5,…中，前()个数中有个()的函数值，有()-=[()]个()的函数值

因为第[()]个()的函数值为{[()]}，由函数(),()的严格单调性知，(),(+1)不是相邻正整数，所以()={[()]}+1,=1,2,3,…

通过简单分析计算可以得到，(),()前若干项的取值见表3，发现(),()的函数值的对应规律符合另一个数列{}的特征，该数列定义为：===1,=-1+-3,=3,4,5，…，即数列某一项等于其前一项与其前三项之和，有=2,=3,=4,=6,=9，…

表3 推广形式二：u(x),v(x)前若干项的取值

表3中前4个正整数对应了3个()的函数值和1个()的函数值，前6个正整数对应了4个()的函数值和2个()的函数值，前9个正整数对应了6个()的函数值和3个()的函数值，前13个正整数对应了9个()的函数值和4个()的函数值，涉及的(),()函数值的个数均为数列{}某一项的取值

由此可以猜测以下结论，并采用数学归纳法进行严格证明

对()=[()]+,∈的情形有：在任意前(≥3)个正整数1,2,3,…,中，恰有-1个的元素[即()的函数值]和-3个的元素[即()的函数值]

由表3可知，对=3,4,5,6,7皆成立

假设对3≤≤结论成立，即有

{1,2,3,…,}={(1),(2),(3),…,(-1)}∪{(1),(2),(3),…,(-3)}

由此归纳假设，可知

{(1),(2),(3),…,(-1)}

={[(1)],[(2)],…,[(-2)]}∪{[(1)],[(2)],…,[(-4)]}，

从而有{1,2,3,…,}={[(1)],[(2)],[(3)],…,[(-2)]}∪{[(1)],[(2)],[(3)],…,[(-4)]}∪{(1),(2),(3),…,(-3)}

由前文所得()={[()]}+1,=1,2,3,…可知，

{(1),(2),(3),…,()}={(1)-1,(2)-1,(3)-1,…,(-2)-1}∪{{[(1)]},{[(2)]},…,{[(-4)]}}∪{[(1)],[(2)],…,[(-3)]}

(1)若(-2)-1=()，即(-2)=()+1，则正整数列前()+1个数对应的函数值为(1),(1),(2),(3),…,(),(-2)，也就是有个()的函数值和-2个()的函数值；

(2)若(-2)-1<()，且显然(-1)-1>()，所以正整数列前()个数对应的函数值恰有个()的函数值和-2个()的函数值

因为+1=+-2，所以正整数列前+1个数中有个()的函数值和-2个()的函数值，于是结论对=+1也成立，证毕

在推广形式二中的对应规则下，还可以得到以下推论

对()=[()]+,∈的情形，对任意正整数≥3，≥3，数列+1,+2,+3,…中前项有-1个的元素[即()的函数值]和-3个的元素[即()的函数值]

本文对一个有关函数值求解的问题进行研究，发现函数值的对应规律中隐含着斐波那契数列，并根据正整数集的性质，采用数学归纳法对结论进行了严格证明在此基础上将条件()=[()]+1推广为()=[()]+和()=[()]+，发现在这两种推广情形下，函数值的对应规律中也隐含着斐波那契数列延伸和变形后的特征在今后的研究中，我们可以考虑将条件进一步推广为()=[()]+，()=[()]+等其他更复杂的形式，以此继续深化研究成果