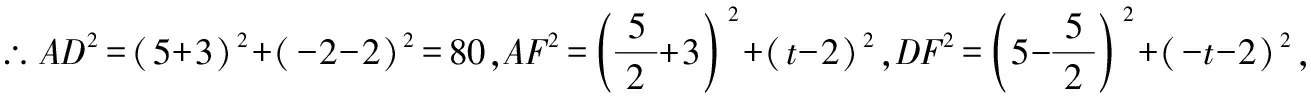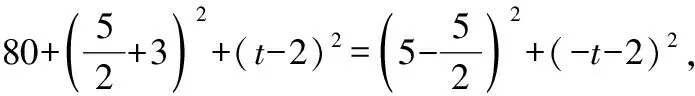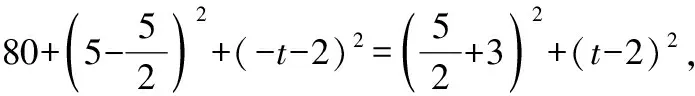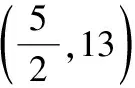漫谈直角三角形存在性问题的解法

◎韩 强

(山东省东营市利津县凤凰实验中学，山东 东营 257400)

2020年江苏无锡中考题：二次函数=-3+3的图像过点(6,0)，且与轴交于点，点在该抛物线的对称轴上，若△是以为直角边的直角三角形，则点的坐标为________

一、基本解法展示

基本解法1：=-3+3，当=0时，=3，

∴点坐标为(0，3)，

∵∠1+∠2=90°，∠2+∠3=90°，

∴∠1=∠3，又∠=∠=90°，

∴△∽△，

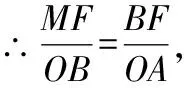
∴=6，

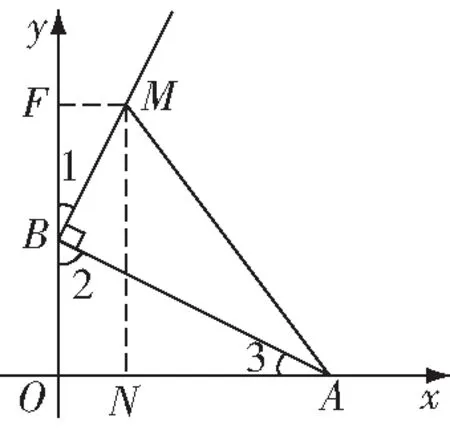
图1

图2

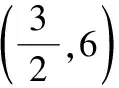
基本解法2：=-3+3，当=0时，=3，

∴点坐标为(0，3)，

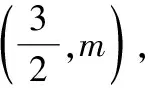
=+=6+3=45,

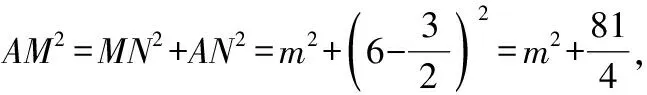
∵∠=90°，

∴=+，

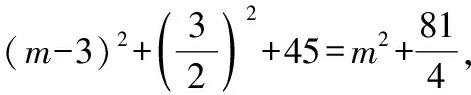
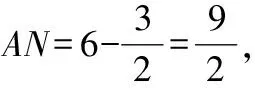
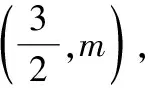
=+=6+3=45,

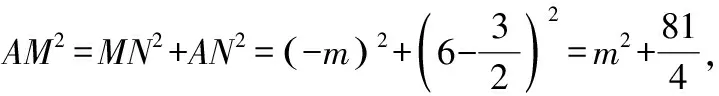
∵∠=90°，

∴=+，

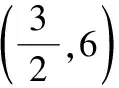
二、两种基本解法的联系与区别

基本解法1主要运用的是相似三角形的知识，基本解法2则主要运用的是勾股定理的知识两种解法都是经典的巧妙解法，基本解法1创造性水平极高，是把“直角三角形存在”的条件进行了等价替换，使之转化成了两个直角三角形相似，然后运用分式方程求解，基本解法2是相对直接的思路，它直接运用勾股定理得到关系式，设定参数，并运用直角三角形中的勾股关系表达目标直角三角形的三边平方，列整式方程求解解法1构图精妙，解法2计算绝妙，根本区别还是思维的方向和运用知识点的不同解法1相对来说属于“曲线救国”，适合思维能力较强的学生掌握，解法2则表现得比较直来直去，适合思维能力较弱的学生掌握教师在教学中两种解法都应教给学生，但是应把解法2放在前面讲授

其实，勾股定理何尝不是由几个相似直角三角形对应边成比例的关系式推演得到的呢？射影定理中就包含了三个直角三角形循环相似的内容和勾股定理的结论这是直角三角形存在性问题能有两种基本解法的根本原因直角三角形存在性问题的最主要的条件就是“直角的存在”，我们将“存在直角”的条件理解成两个锐角互余的条件，就有了寻找两个直角三角形相似的解法1，而将“存在直角”的条件理解成三边所满足的勾股关系的条件，就有了直接列出整式方程的解法2解法1还有“弦外之音”，值得深究和挖掘，而解法2就显得“孤苦伶仃”了我们不妨把解法1叫作相似转化法，把解法2称为勾股定理法

三、相似转化法的构图策略

由解法1的构图思路，我们将和相似无关的条件删除，把二次函数的背景删除，不难发现，基本的图形有下面两种，如图3和图4

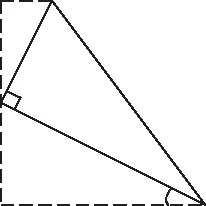
图3

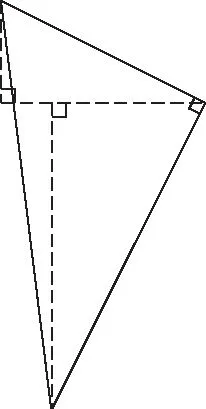
图4

其实，构造相似的直角三角形就是解法1的基本策略我们只有构造出合适的图形才能利用相似列出需要的比例式，并利用分式方程求出线段长下面的两道中考题就是该题型与反比例函数和矩形结合的例子

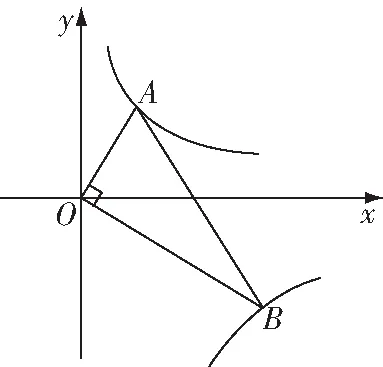
图5

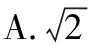
图6

图7

2020年山东烟台中考题：如图8，在矩形中，点在上，将矩形沿折叠，使点落在边上的点处若=3，=5，则tan∠的值为( )

图8

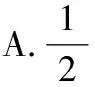
(勾股定理法)∵四边形为矩形，

∴==5，==3，

∵矩形沿直线折叠，顶点恰好落在边上的处，

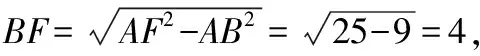
∴=-=5-4=1

设=，则==3-在Rt△中，

∵+=，

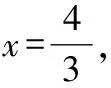
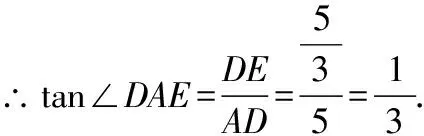
故选D.

试思考一下，用第一种基本解法——相似转化法如何求解？

四、直角三角形存在性问题的特殊解法

这类问题中有的加了限定条件“以某条已知线段为直角边”，这样直角三角形存在的可能情况就减少了，不加此条件答案一般有四种

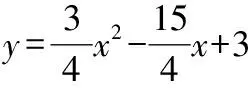
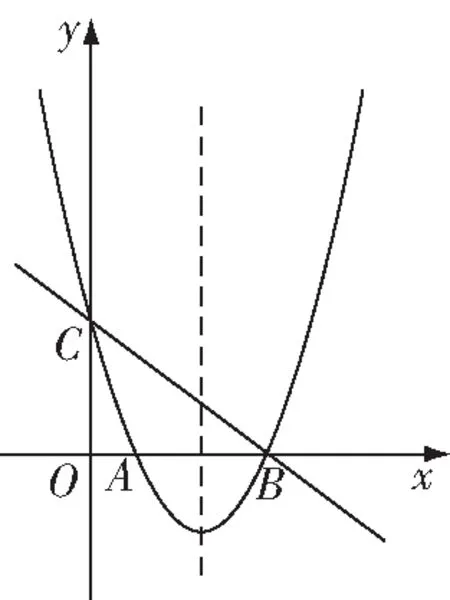
图9

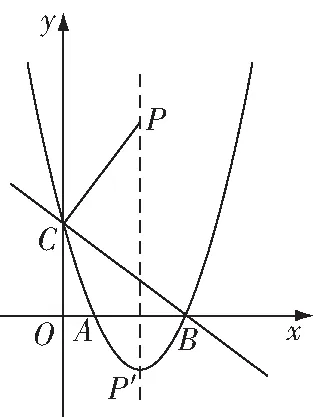
图10

存在如图10所示，

(1)当⊥时，△为直角三角形，

根据两直线垂直时斜率的关系，

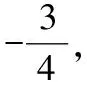
又∵直线经过点，

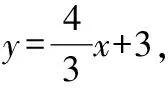
(2)当′⊥时，△′为直角三角形，

又∵直线经过点(4，0)，

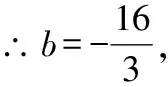
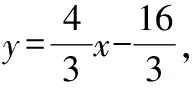
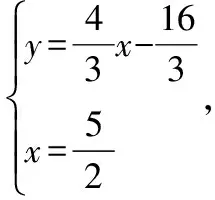
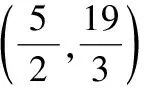
五、两种基本解法的选择方案

尽管两种基本解法都是万能的，但是不同题目的特点决定了我们选择哪种方法一般情况下，如2020年江苏省无锡市的中考题加了直角边限定条件，构图比较简单，我们可以用相似转化法，如果没有这个条件，我们就直接用勾股定理法如下面的题目和解析，我们单纯从得分和省时间的角度看，直接用勾股定理便于分类，且不必画太多的图下面的中考改编题有四个答案，我们如果用基本解法1，必须完成四个图，非常烦琐，若直接用勾股定理法，则后面的解析步骤整齐简洁

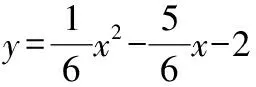
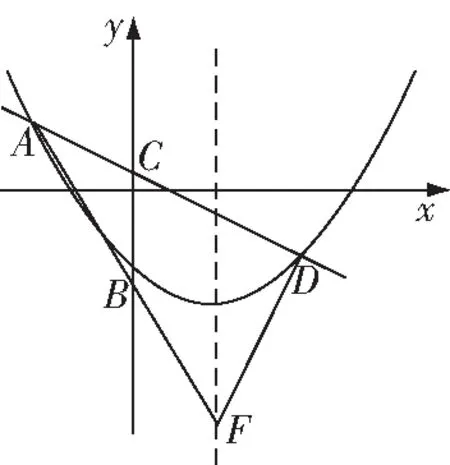
图11

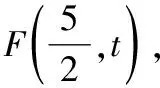
∵(-3，2)，(5，-2)，