可重复使用运载火箭着陆支腿总体布局与关键参数优化
2022-09-23翟海涛王梓尧王铭刚徐国伟
汪 融,翟海涛,王梓尧,王铭刚,徐国伟
(航天科工火箭技术有限公司,武汉 430040)
0 引 言
目前运载火箭回收方式主要包括伞降回收、伞降加气囊回收、有翼水平回收、旋翼方式以及着陆缓冲机构垂直回收。其中垂直起降方式具有落点便于控制、地面支持系统简单等优势,在国际商业发射市场上应用越来越广泛。
着陆支腿一般可分为三腿式、四腿式以及多腿式。着陆腿的数量对着陆稳定性起着至关重要的作用,通常情况下支腿数量越多,着陆稳定性越好,对应的支腿总质量越重。
由美国麦道公司研制的DC-X垂直起降运载器采用了三级支柱式结构,通过置于三级支柱上方的空气活塞开展和回收。简单支柱连接方式结构简单,重量较轻,传递载荷直接,但为保留足够的缓冲行程,支柱较长,受力方式较差,重心较高。
SpaceX公司研制的猎鹰九号运载火箭采用了外翻倒三角结构形式,采用多级伸缩套筒原理来实现展开动作。倒三角式结构的受力情况比较简单,易于辅支柱与主体结构的连接,对着陆地形适应较差,适用于集中载荷作用的情况;着陆腿张开的角度比较大,稳定多边形外接圆直径较大,着陆稳定性高。
蓝色起源公司的“新谢泼德”火箭是通过平行四边形连杆实现折展,利用斜拉连杆增强机构稳定性,连杆底端安装有缓冲器,飞行过程中支撑机构收拢以减小空气阻力,着陆前将平行四边形连杆展开并锁定提供支撑。但是该支撑机构布置形式影响火箭发动机安装空间。
近年来国内也在不断探索研究可重复使用运载火箭着陆支腿,南京航空航天大学肖杰等研制了外翻式气动展开着陆支腿,并对气动收放性能进行了仿真分析。朱冠宁等运用能量法建立了着陆支腿的数学模型,对着陆支腿的总体布局设计参数进行优化,并开展了仿真验证。哈尔滨工业大学田保林等通过图论法对着陆支腿折展方案进行拓扑分析,完成支腿构型方案优选,并对支腿结构参数进行优化。上述支腿均是直接参照SpaceX公司研制的猎鹰九号运载火箭的构型,未对支腿数量及构型进行对比分析,同时设计参数优化均是基于数学模型,而数学模型较为理想,不能真实地反映整个着陆过程。
本文基于对支腿数量及支腿构型的对比仿真分析结果,提出了可重复使用运载火箭着陆支腿的总体布局方案,同时建立了着陆支腿参数化仿真模型,基于多体动力学仿真软件开展着陆稳定性仿真分析,以着陆稳定性、运载火箭返回级受到的着陆过载系数及支腿轻量化为优化目标,对着陆支腿关键几何参数进行优化和确定。
1 关键几何参数及参数化仿真模型建立
1.1 关键几何参数
本文研究对象为直径为3800 mm的可重复运载火箭返回一子级,返回质量约24t,箭体质心距离箭体底部距离为11088 mm,为确保着陆安全性,着陆支腿展开后箭体底部与地面之间要有一定的安全间隙。着陆支腿完全展开后的箭体下端离地高度一方面与着陆支腿的缓冲性能相关,另一方面与着陆支腿几何参数相关。着陆支腿关键几何参数主要指着陆支腿展开半径,即足垫中心到箭体对称面距离以及着陆支腿与水平地面的夹角,具体如图1所示。

图1 着陆支腿参数示意图Fig.1 Schematic diagram of the landing leg parameters
1.2 参数化仿真模型建立
在多体动力学仿真软件中,根据着陆支腿安装位置创建相关的设计点,然后以参数化点坐标的方式进行参数化建模,并根据支腿具体结构形式设置对应的连接副。其中主支腿与缓冲器设置移动副和弹簧,模拟缓冲器的压缩过程。外翻倒三角式着陆支腿参照SpaceX公司的猎鹰九号运载火箭着陆支腿的构型,平行四边形连杆形式着陆支腿参照蓝色起源公司的“新谢泼德”火箭着陆支腿的构型,参数化仿真模型如图2所示。设置仿真参数见表1。

图2 着陆支腿参数化仿真模型Fig.2 Parametric simulation model of landing legs

表1 仿真参数Table 1 Simulation parameters
1.3 稳定距离判别准则
本文稳定性分析基于稳定距离判别准则,如图3所示,4个外围的小黑点为着陆过程中4个足垫在着陆平台上的投影,中间小黑点为火箭重心在着陆平台上的投影。4个足垫在平台上的投影点所形成的闭合曲线为稳定多边形。将重心在着陆平台上的投影点到稳定多边形四条边的距离最小值作为判断火箭能否稳定着陆的条件,因此只要满足min(,,,)>0,火箭就不会翻覆。

图3 火箭着陆稳定距离判别Fig.3 Landing stability distance discrimination of the launch vehicle
2 着陆支腿总体布局设计
2.1 着陆支腿数量确定
以外翻倒三角式着陆支腿为例,设置单条支腿质量一致(约为400 kg),除支腿数量不同外其余设计参数均一致(辅支柱位置距离尾段端面为500 mm,展开半径为7000 mm、夹角为45°),给箭体三个方向分别添加5 (°)/s的初始角速度进行仿真,支腿不同时着陆,仿真结果如图4所示。三、四、五条腿在接触地面后箭体均出现回弹,其中四条腿时箭体回弹最少,三条腿和五条腿稳定时间更长。根据图4(a),着陆支腿数量越多,稳定距离越大,稳定性越好,四条腿稳定距离相对于三条腿增大40%,五条腿稳定距离相对于四条腿增大约15%,随着腿的数量增大,稳定距离增加的幅度减少,但是质量增加却很大。三腿着陆器要达到相同质量四腿着陆器相同的稳定性,着陆腿的最大跨度要求至少达到四腿着陆器着陆腿最大跨度的两倍。根据图4(b),相对于三条着陆支腿构型,四条腿与五条腿着陆后箭体下端离地高度较大,且相差不多,而且三条腿时箭体与地面发生碰撞。根据图4(c),三条腿时箭体出现抖动,箭体过载系数波动变大,稳定性较差。

图4 不同数量支腿仿真结果Fig.4 Simulation results of different numbers of legs
综上所述,对各主要数量着陆支腿性能总结见表2。着陆支腿数量越多,稳定距离越大,稳定性越好,但是稳定性增加的幅度随着支腿数量的增加不断减少,质量增加很大。着陆腿长度的增大会增加支腿的设计难度,综合考虑稳定性和质量,确定可回收火箭着陆机构的着陆腿数量为四条,均匀分布在箭体四周。

表2 不同数量着陆支腿性能对比表Table 2 Performance comparison of different numbers of landing legs
2.2 着陆支腿结构形式确定
着陆支腿结构形式主要考虑倒三角式和平行四杆式,倒三角式四腿模型参数设置见上节,设置平行四杆式结构形式单条支腿质量一致(约为400 kg),所有设计参数均与倒三角式一致(辅支柱位置距离尾段端面为500 mm,展开半径为7000 mm、夹角为45°)。考虑到火箭着陆时存在横向姿态偏差、角加速度和水平速度,着陆支腿很难同时着陆,给箭体分别添加初始角速度5 (°)/s(三个方向),初始水平速度1 m/s,横向姿态偏差5°,进行仿真分析,仿真结果如图5所示。根据图5(a),倒三角式支腿稳定角度和稳定距离更大,稳定性更好;根据图5(b)和图5(c),平行四杆式支腿垂向承载更好,箭体过载系数也更小,箭体下端离地高度更大;根据图5(d),平行四杆式支腿在存在横向姿态偏差和水平速度时会发生跳跃,不利于箭体的稳定。

图5 不同构型仿真结果Fig.5 Simulation results of different configurations
综上所述,倒三角式支腿稳定距离更大,稳定性更好。平行四杆式支腿垂向承载更好,箭体过载系数也更小,箭体下端离地高度更大。但是平行四杆式支腿容易受到横向姿态偏差、角加速度和水平速度等因素的干扰,火箭着陆时有可能会发生跳跃,不利于箭体的稳定。综合考虑结构复杂度、气动性及稳定性等因素,确定着陆支腿构型为倒三角式。
3 着陆支腿关键几何参数确定
3.1 支腿一般设计参数定义及确定
外翻倒三角式着陆支腿相关参数如图1所示。各参数含义见表3。

表3 着陆支腿相关结构参数Table 3 Relevant structural parameters of landing legs
仿真分析对箭体着陆影响,结果见表4,随着辅支柱与箭体连接点的横向距离增大,稳定距离变小,稳定性变差。但是箭体最小箭体下端离地高度变大,箭体垂向过载系数变小,最大缓冲力和最大接触力变小。为了减小箭体着陆冲击时的过载系数,辅支柱与箭体连接点的横向距离需要尽量增大,同时考虑需预留一定的安装距离,将辅支柱与箭体连接点的横向距离设为2400 mm。
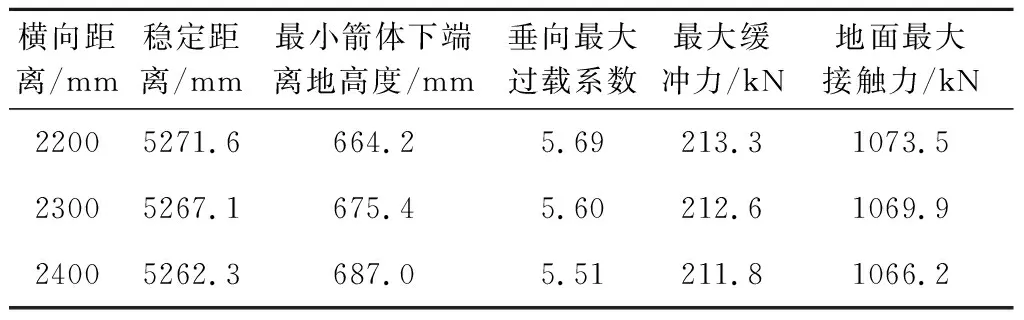
表4 不同横向距离仿真结果极限值对比表Table 4 Comparison of limit values of simulation results for different lateral distances
仿真分析对箭体着陆影响,结果见表5,辅支柱距离箭体尾段端面越高,稳定距离越大,稳定性越好,箭体下端离地高度越小,箭体过载系数越大,最大缓冲力和最大接触力变大,而且在距离为1000 mm时,箭体下端离地高度过小,安全间距不够。考虑受力问题,辅支柱安装位置距离尾段端面位置越近越好,考虑预留耳片和限位装置的安装空间,将辅支柱箭体尾段端面的高度设为500 mm。
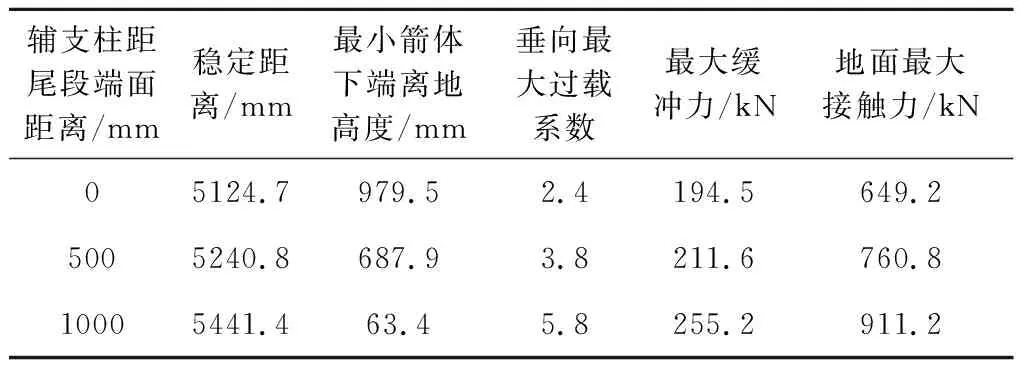
表5 不同辅支柱位置仿真结果极限值对比表Table 5 Comparison of limit values of simulation results for different auxiliary pillar positions
为防止发动机喷嘴与地面发生碰撞,同时考虑着陆稳定后,箭体与地面需要预留一定的安全间隙,为2500 mm。
3.2 着陆支腿关键设计参数定义及范围
展开半径和主支腿与水平地面夹角直接决定整个支腿外形,且对支腿着陆稳定性、箭体过载系数及箭体下端离地高度等结果影响较大,因此将展开半径和主支腿与水平地面的夹角确定为优化设计变量。为简化计算,考虑箭体下端点中心轴、上端点中心轴在竖直方向上共线,且根据火箭总体外形要求,上端点位置距离尾段端面不超过6800 mm。
根据多轮仿真研究,极限工况为箭体分别添加初始角速度5(°)/s(三个方向),初始水平速度1 m/s,两个横向姿态偏差为5°,该种情况下双腿先同时着陆。考虑到在初始着陆时,箭体质心在地面上的投影应该位于4个足垫在平台上的投影点所形成的稳定多边形内部,否则在初始角速度和水平速度影响下,箭体肯定会失稳。因此本文对箭体着陆时的初始姿态进行分析,确定展开半径及夹角的初步范围。
假设箭体质心初始状态在水平地面的投影为(0 mm,0 mm),在两个横向姿态偏差5°影响下(-和+两个方向),箭体质心在地面的投影点坐标为(-962.7 mm,966.4 mm),在MATLAB中计算分析展开半径对初始稳定性的影响,确定着陆前四个支腿及箭体在水平地面的投影,从而确定出稳定多边形,分析结果如图6所示。

图6 展开半径对稳定性的影响Fig.6 The influence of unfolding radius on stability
根据图6,当展开半径大于2400 mm时,初始状态最小稳定距离大于零。为了确保在初始角速度和水平速度影响下,箭体不会失稳,展开半径应大于2400 mm。
根据上述分析,初步确定展开半径的变化范围为[2500 mm,9500 mm],变化增量为200 mm,夹角的变化范围为[10°,85°],变化增量为5°。基于多体动力学仿真软件中命令行实现极限工况仿真控制,同时将上述三个需满足的条件作为必要条件,将仿真结果输出进行分析。各种情况对应的箭体下端离地高度如图7所示。
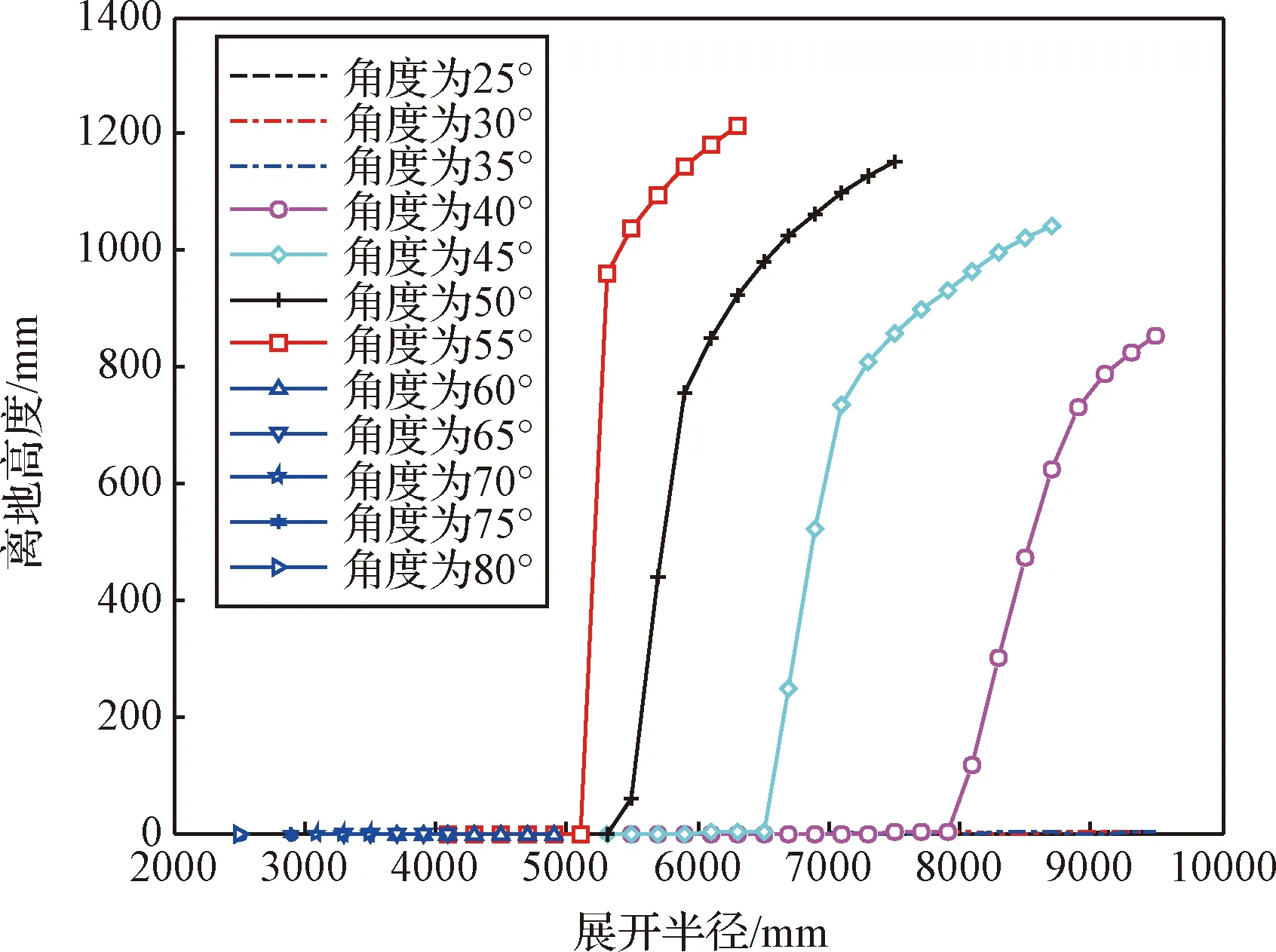
图7 箭体下端离地高度示意图Fig.7 Schematic diagram of the height of the rocket body from the ground
根据图7,当夹角小于40°和大于55°时,箭体最小箭体下端离地高度为0 mm,说明箭体已经倾倒。同时当箭体展开半径大于5300 mm时,箭体才不会发生倾倒。考虑支腿总质量上限要求,展开半径不超过7500 mm。同时考虑初始仿真步长过大的影响,确定展开半径优化设计范围为[5100 mm,7500 mm],夹角优化设计范围为[35°,60°]。
3.3 支腿关键设计参数优化
针对极限着陆工况开展仿真优化分析,设置展开半径的变化范围为[5100 mm,7500 mm],变化增量为100 mm,夹角的变化范围为[35°,60°],变化增量为1°。基于多体动力学仿真软件中命令行实现仿真控制,并将满足指标要求的仿真结果输出分析。
支腿不同时着陆,仿真结果如图8所示。展开半径为5600 mm时,角度要大于51°才能满足着陆过程中箭体与地面安全距离大于600 mm的要求。展开半径为7500 mm时,角度大于44°即可满足稳定后箭体与地面安全距离要求。

图8 极限着陆工况仿真结果Fig.8 Simulation results of extreme landing conditions
当展开半径一定时,夹角越大,着陆支腿总质量越大,稳定距离越小,稳定性越差,箭体下端离地高度越大,箭体垂向着陆过载系数越大,缓冲力随角度的增加而减少。
当角度一定时,展开半径越大,着陆支腿总质量越大,稳定距离越大,稳定性越好,箭体离地安全距离也越大,箭体垂向着陆过载系数越小,缓冲力越小。
基于Pareto解集的多目标优化算法有多种,本文通过定义支配关系以及排序,确定数据集合中不被支配或排位在前的数据点,构成最优解集。
对于如下的多目标优化问题:
min(max)()=min(max)((),…,()),∈
(1)
支配关系是指:对于可行解和,如果∀∈{1,2,…,},()≤(),且∃∈{1,2,…,},()<(),则称可行解支配可行解。若没有可行解可以支配,则为Pareto最优。
排序分配是指:在一组解中,非支配解Pareto等将着陆支腿质量()、着陆最小稳定距离()、最大缓冲力()、箭体最大过载系数()作为目标函数进行优化,着陆支腿系统多优化目标如下:
级定义为1,将非支配解从解的集合中删除,剩下解的Pareto等级定义为2,依次类推,可以得到该解集合中所有解的Pareto等级。同时用局部拥挤距离来表示个体在非支配集合中所处位置的密集程度。
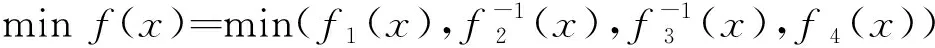
(2)
其中为展开半径与夹角的组合。
对满足要求的仿真进行排序和拥挤度计算,得到等级1中拥挤度较大的Pareto最优解见表6。
根据表6,展开半径和角度的设计组合最优解对应的支腿质量、稳定性、缓冲力及着陆过载系数相对较优,可根据不同型号结构舱段布置、总体指标要求来选定展开半径和角度,本文研究对象为直径3800 mm的可重复运载火箭返回一子级,返回质量约24t,与SpaceX公司猎鹰九号返回级参数接近,根据箭体舱段布置及总体指标要求,最终确定关键参数展开半径为7100 mm,角度为45.5°。根据该参数建立的支腿与SpaceX公司猎鹰九号支腿外形比例较为一致,说明本文这种优化设计方法在工程上有一定的实践指导意义。
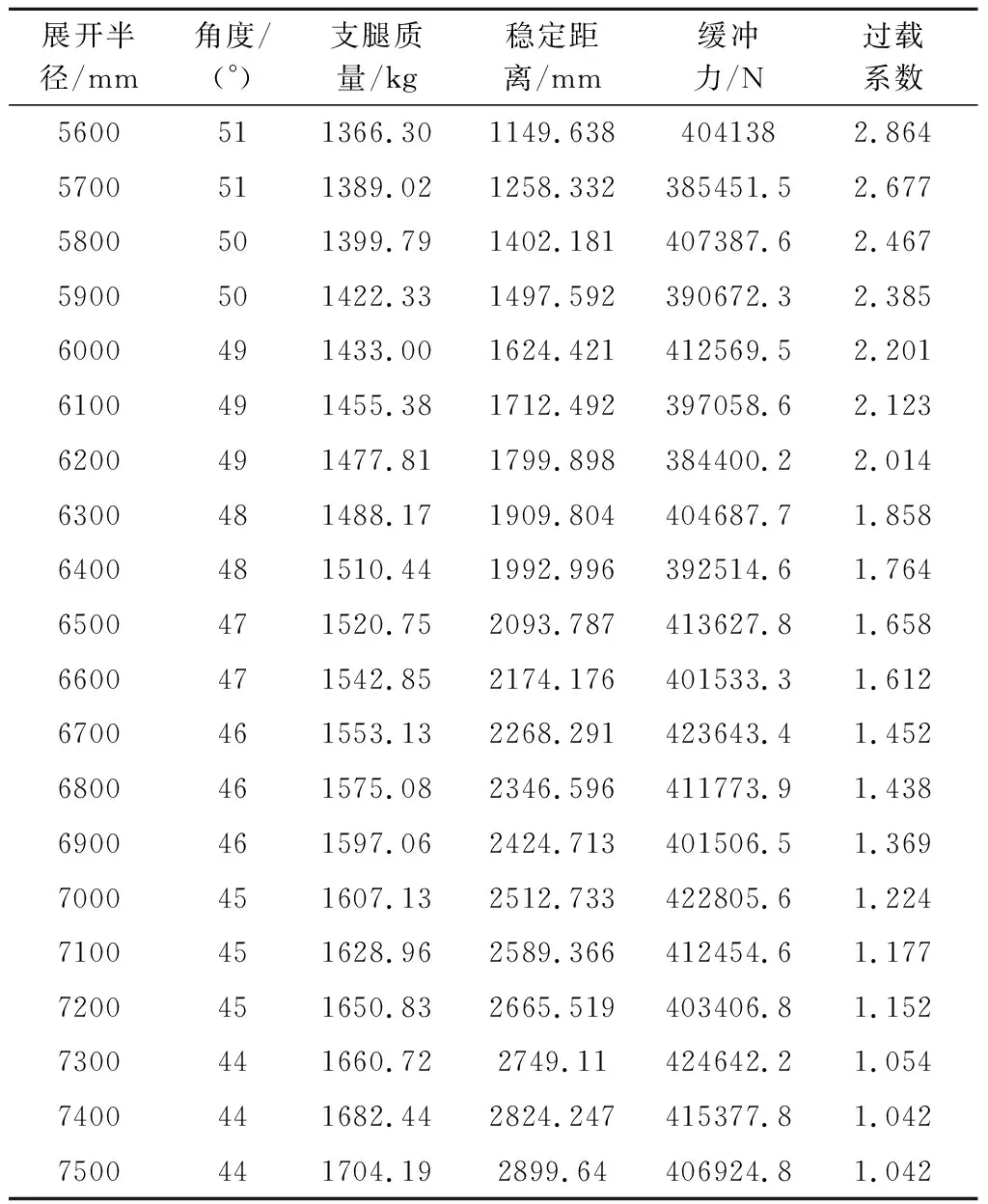
表6 Pareto最优解Table 6 Pareto optimal solution
4 结 论
(1) 基于对支腿数量的对比仿真分析,四条腿稳定距离相对于三条腿增大40%,五条腿相对于四条腿增大约15%,随着腿的数量增大,稳定距离增加的幅度减少,但是质量增加却很大,综合考虑着陆稳定性和质量,选用四腿布局。
(2) 基于对支腿构型的对比仿真分析,发现不同时着陆工况下平行四杆式支腿会发生跳跃,不利于箭体的稳定,而外翻倒三角式着陆稳定性较好,因此最终确定选用外翻倒三角式结构型式。
(3) 基于多体动力学仿真分析及Pareto解集的多目标优化算法,确定展开半径和角度最优解集,其对应的支腿质量、稳定性、缓冲力及着陆过载系数相对较优,该方法可以为未来着陆支腿的参数确定提供相应的技术支持。
