基于TRMF-LSTM组合模型的多维时间序列预测

曹超凡，李 路

（上海工程技术大学数理与统计学院，上海 201620）

0 引言

时间序列问题一直以来都是一个热门研究话题。传统研究模型如自回归模型（AR）、移动平均模型（MA）和移动自回归模型（ARMA）对小样本平稳时间序列数据预测起到了非常好的效果［1］。对于小样本非平稳时间序列也有相应的方法，例如差分引入形成ARIMA 模型［2］，但引入差分的方法可以充分提取确定信息，却很难对模型进行直观解释。由此开始对残差进行自回归，建立残差自回归模型（Residual Auto-Regressive）［3］，而为了能够准确模拟时间序列的波动性，Beran［4］提出ARCH 模型和GARCH，用于处理具有异方差性和异方差自相关的时间序列数据。而对于处理多维时间序列，向量自回归模型（VAR）模型作为AR 模型的高维扩展起到了很好的预测效果［5］。

近些年，随着大数据与人工智能的快速发展，人们研究的数据量和数据维度急剧增长，多维时间序列数据开始频繁走进研究人员的视野。在股票市场中，股价数据本身具有非线性、非平稳等复杂特点，精准预测股票时间序列是投资者十分关注的话题［6］。

在时间序列分析中，传统的时间序列模型在处理小样本、线性且平稳性数据时具有无可比拟的优势。但在处理大样本、非线性、非平稳数据时效果较差，并且存在计算成本大、最优化难以实现等问题［7］。随着信息技术的发展及大数据时代的到来，深度学习技术的引用使时间序列分析模式变得更加成熟［8］。Yu 等［9］将广义线性自回归(GLAR)与人工神经网络（ANN）相结合对时间序列进行预测，实证结果显示其预测精度更高。Elman［10］以序列的演进方向进行递归，提出第一个具有记忆性的循环神经网络（RNN），但随着时间长度的增加，神经网络参数呈指数增长，简单的RNN 无法解决由时间长度带来的梯度爆炸和梯度消失问题［11-12］。Hochreiter 等［13］为解决循环神经网络长期以来存在的问题，提出长短期记忆网络（Long Short-Term Memory networks，LSTM），解决了RNN 具有的长期依赖性问题。

而在股票时间序列预测中，股票数据自身具有较强的复杂性，同时具有线性和非线性部分。传统的时间序列模型可以很好地处理时序数据的线性部分，当前火热的深度学习技术可以更加灵活地处理时序数据的非线性部分，但单一的模型只能侧重研究时序数据的某一方面特征，对时间序列数据进行预测会不可避免地丢失部分信息，无法同时兼顾线性与非线性部分［14］。由此，学者开始研究组合预测模型，融合线性预测模型与非线性预测模型的特点，将深度学习与传统的时间序列模型结合起来，发挥各自优势，构建各类组合预测模型，增强了时间序列预测的适用性，并达到更高的准确率。吴晓峰等［15］提出基于BP 神经网络误差修正的ARIMA 模型，优化了时间序列非线性拟合部分。刘胤池［16］在用ARIMA 模型处理线性特征的基础上，利用SVM 对非线性数据处理优势拟合残差。王越敬［17］提出LSTM-ARIMA 混合模型以预测股价相关系数，使模型具有较好的稳定性和泛化能力。

综上所述，学者在组合预测模型上有了较为深入的探究，但多数研究是将传统的ARIMA 模型与机器学习模型融合，只能处理一维时间序列，对多维时间序列鲜有涉及。而像股票数据，常常需要涉及到多个股票因子数据，针对此问题，本文在基于组合预测的思想，引入可以处理多维时间序列的时序矩阵分解技术（Temporal Regularized Matrix Factorization，TRMF），该理论融合了可处理多维时间序列的VAR 模型与矩阵分解技术，可以很好地处理线性数据。将其与LSTM 模型相结合，提出了TRMF-LSTM 组合预测模型，用TRMF 预测股价数据的线性部分，再用LSTM预测股价数据的非线性部分，为股票多维时间序列预测提供一个新的思路与方法。

1 基本理论

1.1 时序正则化矩阵分解模型

在处理多变量时间序列数据时，通常需要同时接触到时间长度、变量数，可用矩阵表示多维时间序列数据结构。本文根据多元时间序列结构构建多元时序矩阵Y∈RN×M，假设矩阵Y表示一支包含N 个属性M 个时间步长的时序矩阵，如式（1）所示。

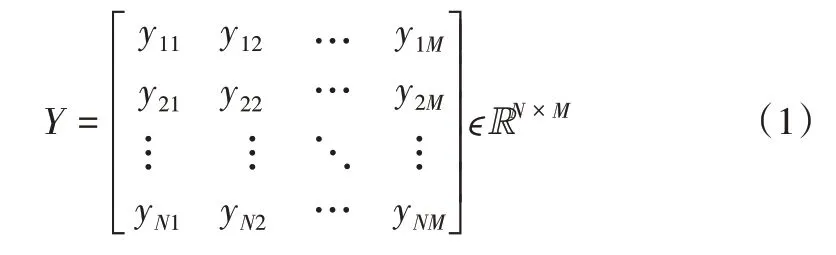
Y的每一行向量表示某一属性的时间序列，即该属性值随时间演进方向的变化趋势。Y的每一列向量表示在相同时间维度上，各属性值所构成的当前状态。为实现对多维时间序列的预测，本文引用低秩矩阵分解技术。

低秩矩阵分解在人工智能领域得到了广泛应用，对时间序列的缺失值起到很好的补全作用，并可以直接从部分观测的时间序列数据中进行观测和学习。Chen 等［18］首次使用矩阵低秩分解技术处理时空数据。Yu［19］考虑到时间相关性，提出时间正则化矩阵分解模型（Temporal Regularized Matrix Factorization，TRMF）实现对高维时间序列的预测。Chen 等［20］将在自回归模型作为典型的时序模型与低秩矩阵分解结合，并应用到交通时空数据，更好地解决时间序列高相关性的特点。

根据该时序矩阵具有的时间与属性两个维度，将多元时序矩阵进行低秩分解，得到两个矩阵，如式（2）所示。

其中，矩阵W为R×N维的属性矩阵，矩阵X为R×M维分解后的时序矩阵，估计出矩阵W和X，便可得到Y的估计矩阵元素表示为矩阵第i个属性，第j个时间点的数据，其估计值计算公式如式（3）所示。

其中，wi为样本矩阵的第i列向量，xj为时序矩阵X的第j列向量，即为第j个时间点的R维向量。

现假设被分解后得到的时序矩阵X第t列向量xt为多元时间序列第t个时间点的向量，其有N个分量，即xt=(x1t，，x2t，…xRt)T。其中，xit表示多元时间序列第t个时间点第i个分量的值，而向量(x1，x2，…，xM)构成了时序矩阵X，如式（4）所示。

矩阵X每一行向量表示一条单变量时间序列，矩阵X每一列向量表示多元时间序列的某一时间点对应的序列向量，而由于时间序列具有自相关性，假设时序列向量xt与前几列向量存在着强相关性，代入VAR 模型，可用如式（5）所示方程描述。

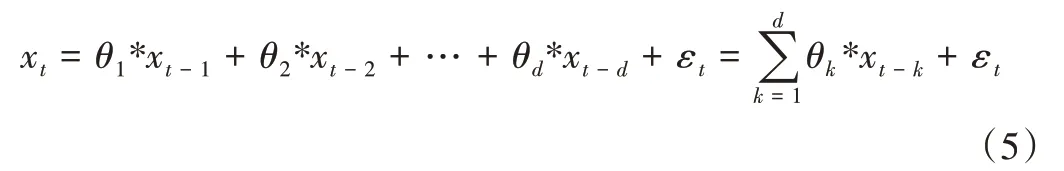
其中，θk表示时序回归系数向量，d表示回归阶数，xt-k表示为时序矩阵X第t-k列向量，*表示向量对应元素相乘。将时序回归系数向量拼成矩阵形式θ，最终可表示为如式（6）所示。

构建的时序矩阵分解的优化问题可以表示为如式（7）所示。

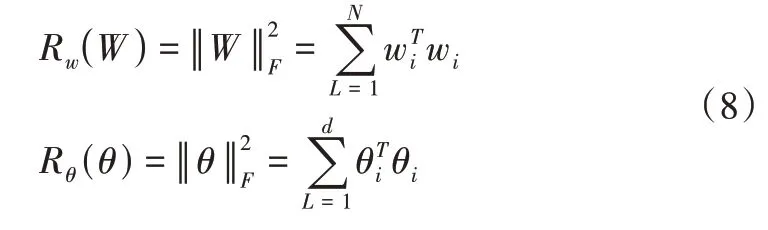
优化问题即式（7）的第三项考虑时序矩阵X列向量存在着时序关系，在矩阵分解的基础上引入时序正则项，以自回归的方式对自适应该系统的时序系数矩阵θ、属性矩阵W以及时序矩阵X进行学习，而不用实现人为设定时序系数θ。时序正则项如式（9）所示。

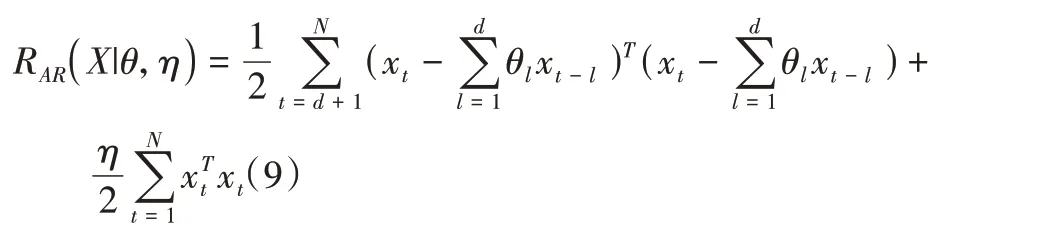
通过求解式（8）的优化问题，采用最小二乘求解方式，可以得到时序矩阵X、属性矩阵W和时序系数矩阵θ 每一项的迭代公式，如式（10）、式（11）、式（12）所示。

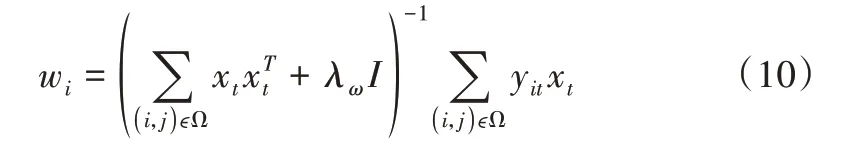
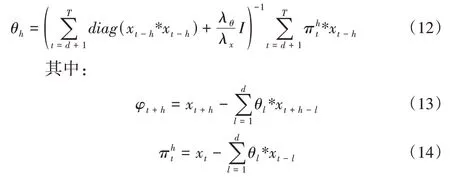
对3 个参数顺着时间的演进方向不断进行更新、迭代，得到完整的属性矩阵与时序矩阵，进而点乘得到预测矩阵，实现时间序列预测。具体算法步骤如下：

Step1：给定初始矩阵W0、θ0、X0及含待预测股票数据的矩阵Y。

Step2：根据式（10）、式（11）、式（12）分别对时序矩阵X、属性矩阵W和时序系数矩阵θ 的每一列向量xt、wi、θh进行交替迭代更新，从而完成新一轮矩阵W、θ、X的更新。

Step3：利用式（5）更新xM+1、xM+2…，得到扩展矩阵Xnew。

总体而言，TRMF 结合了矩阵分解技术与VAR 模型，利用矩阵分解技术实现对时序矩阵的降维，增强了预测鲁棒性，再利用时间的自相关性不断对降维后的时序矩阵进行更新，实现了多维时间序列预测。

1.2 长短期记忆人工神经网络模型

长短期记忆网络（LSTM）是循环神经网络（RNN）的改进模型。为解决RNN 的梯度消失问题，LSTM 添加了细胞状态ci用来存储时间序列的历史信息。LSTM 有3 个门控单元：遗忘门、输入门与输出门，用以处理历史信息与输入信息，进行遗忘与更新。如图1所示。

遗忘门确定从历史信息中筛去哪些对当前状态无影响的信息，遗忘计算过程如下：

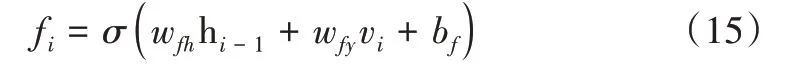
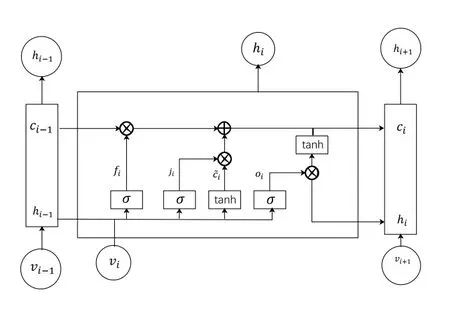
Fig.1 LSTM neural network structure图1 LSTM 神经网络结构

其中，fi是遗忘门的输出；wfh、wfy是权重矩阵，hi-1是上一个存储单元的输出；vi是当前输入；bf是遗忘门的偏置项。σ是Sigmoid 函数，可以将所有激活值映射至0-1 之间，0代表“丢弃”，1代表“保留”。

输入门决定应将哪些当前输入信息添加到细胞状态。更新过程分为两步，第一步计算ji确定需要更新哪些输入信息添加至细胞状态，如式（16）所示。

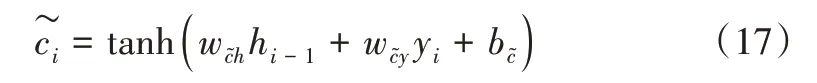
输出门定义确定当前状态需要输出的信息，计算过程如式（19）、式（20）所示。

其中，oi是输出门的输出；woh、woy是权重矩阵；bo是偏差矢量；hi是当前记忆单元的隐藏层输出。

LSTM 因其具有激活函数和门控单元，在处理复杂时间序列，尤其是拟合非线性部分数据时有着较大优势。

2 基于时序矩阵分解与LSTM 的组合预测方法

2.1 组合预测模型理论

大量实验表明，单一模型的预测效果并不能很好地兼顾数据的线性部分与非线性部分。鉴于此，引入组合预测模型，将线性模型和非线性模型的预测优势结合起来，进而提升预测精度。

假设时间序列yt可分为两部分，即线性主体部分Lt和非线性残差部分et，如式（21）所示。

其中，用线性模型预测线性主体部分将最大程度发挥出线性模型的优势，预测结果为，再将真实值与预测值作差，得到残差序列et，再用非线性模型（如深度学习技术）对得到的残差时间序列进行拟合，得到的预测结果为，最后将线性主体的预测部分与非线性残差的预测部分相加，得到组合模型的预测结果，如式（22）所示。

2.2 基于TRMF-LSTM 组合模型方法预测步骤

基于时序正则化矩阵分解的组合预测模型结合了矩阵分解技术与向量自回归模型，利用时间序列的自相关性特点作出预测，通过低秩假设学习全局序列信息，同时引入正则化项，更好地处理过拟合问题，在多元时间序列的线性预测中体现出了自己独特的优势。

但同时，TRMF 处理非线性数据效果较差，而股票数据波动性大，具有非线性、高噪声等特点，同时受政策变动、市场情绪、经济因素等影响，股票时间序列具有高度不稳定性。而深度学习在处理非线性数据有着天然优势，本文将二者优势结合起来，形成矩阵分解与深度学习组合预测的方法。

Step1：首先对多元时间序列数据进行预处理，将多个时间序列进行归一化，处于同一量纲中。

Step2：将多元时间序列按时间节点划分训练集与测试集。

Step3：在训练集中，用TRMF 模型训练数据的线性主体部分，并将序列值yt与其作差，得到残差序列et。

Step4：用et训练LSTM 模型，得到拟合后的残差序列。

Step5：将测试集数据代入训练好的TRMF-LSTM 模型，得到预测线性主体部分与预测残差序列，并将其相加，得到组合模型的预测值，并对其进行反归一化得到最终预测数据。

预测步骤如图2所示。

2.3 评价指标

为了评估TRMF-LSTM 模型在股价预测的准确性，本文选取均方根误差（RMSE）与平均绝对百分比误差（MAPE）两类指标。

这两类指标均衡量预测值与真实值的偏差，越小则表明预测值越接近真实值，即预测精度越高。

3 组合模型实证研究

3.1 数据来源与数据处理

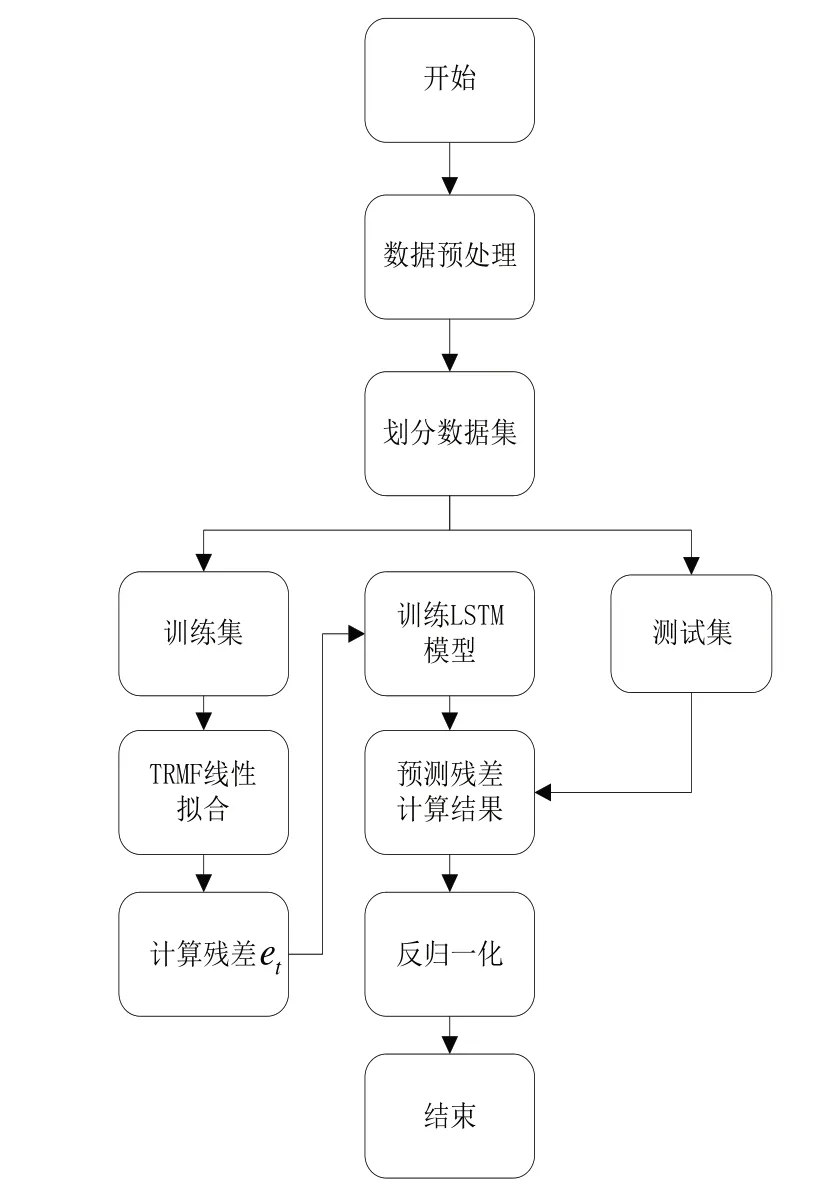
Fig.2 TRMF-LSTM algorithm flow图2 TRMF-LSTM 算法流程

本文数据选取沪深300、上证指数两支股指以及三一重工、中国人寿、农业银行、牧原股份、美的集团、隆基股份6 支个股共8 支股票。通过查阅文献，选取这8 支股票的开盘价、收盘价、最高价、最低价、成交量、成交金额6 个技术类因子，日换手率、流通市值、涨跌幅、市盈率、账面杠杆、现金比率、流动比率、产权比率、销售毛利率9 个质量类因子，净利润增长率、未预期盈余2 个成长类因子，分析师盈收预测变化、10 日乖离率、10 日顺势指标3 个动量类因子，共计20 个股票因子作为模型输入，数据来源于优矿平台，数据时间区间取自2011 年1 月1 日-2021 年3 月7 日，共2 472 条数据，由此构建出股票时序矩阵YN×M，其中N=20，M=2 472。

由于因子间量纲存在较大差异，先对各因子作归一化处理，统一量纲。归一化处理由式（25）所示。

对于获取的股票数据存在缺失值情况，利用矩阵分解技术对历史股价缺失数据进行数据补全，以便于后续模型输入。同时，矩阵分解技术能从带有噪声的时间序列中自动过滤噪声和异常值，在数据处理方面体现了天然的优势。

3.2 参数设置

设训练集与测试集比例为4∶1，由于股票交易日在星期一至星期五，将初始矩阵W0、X0、θ0设置为服从标准正态分布的矩阵，进行单步预测。利用时序矩阵分解技术，构建时序矩阵XR×M与属性矩阵WN×R并不断更新，最终通过点乘求得待预测矩阵,其中将股票时序矩阵YN×M进行降维，构造了时序矩阵XR×M，从而去掉数据集中夹杂的噪声，并增强鲁棒性。TRMF 预测算法基于低秩假设，对于秩R的选取要根据不同股票的时间特性确定最佳选择，通过网格搜索，确定R=8 时，预测效果最佳。对于正则化项λw、λX、λθ均设定为500。选取时间滞后项取前15 项数据，即d=15。

TRMF 算法预测后将预测值与真实值作差得到残差矩阵et，将其转化为含有样本、时间步长、因子属性的三阶张量并输入至LSTM 模型，以收盘价残差序列为标签，设隐藏层节点数设置为50，批量输入batch_size 设置为32，迭代次数epoches=500。拟合出收盘价残差序列后，将其与TRMF对收盘价的预测值相加，即得到股票收盘价的最终预测值。

3.3 实证结果分析

3.3.1 TRMF-LSTM训练结果

将TRMF 拟合原时间序列后，将真实值与其作差，得到残差时间序列。代入LSTM 模型，以沪深300 为例，训练效果如图3所示。

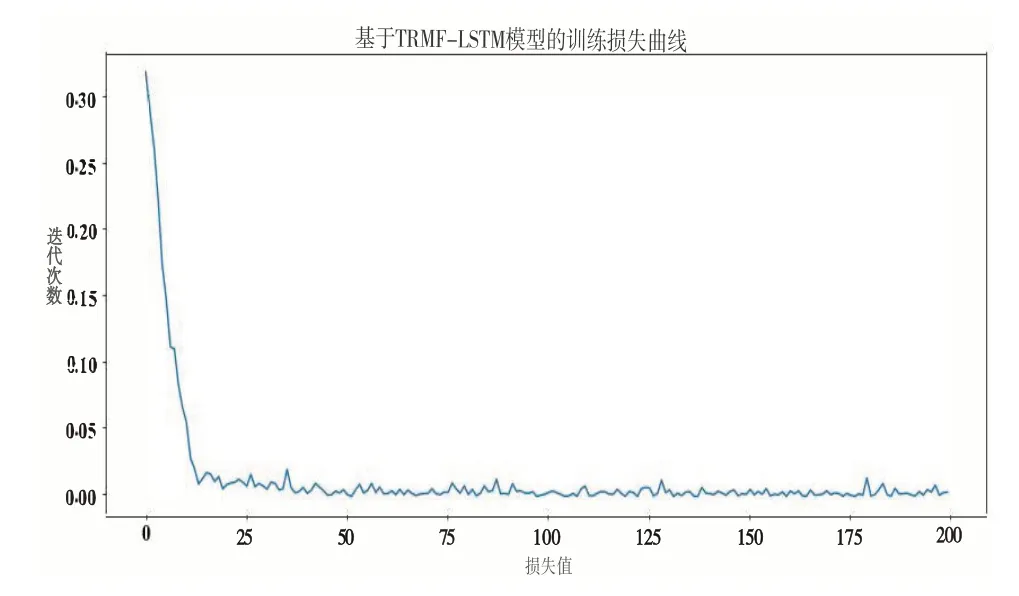
Fig.3 Model training error graph图3 模型训练误差

横轴为迭代次数，纵轴为拟合的损失函数，即：

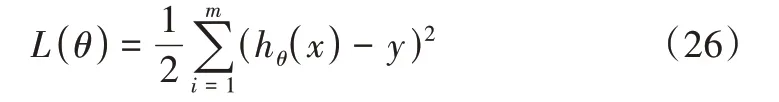
根据模型训练经验，将学习率调为0.01，迭代次数设为500，迭代500 次后即停止训练。可以看出，在训练过程中，迭代15 次时快速收敛，验证了残差训练的有效性。同时，误差波动稳定在0.01左右，体现了模型的稳定性。

3.3.2 TRMF-LSTM组合预测模型与对比模型预测效果

本文采用TRMF-LSTM 组合预测模型，将预测结果与深度学习LSTM 模型、Transformer 模型、传统机器学习支持向量回归SVR 预测的结果作比较，取最后100 天的预测结果。图4—图11 为TRMF-LSTM 预测结果与真实值的对比，横轴为时间，以天为单位，纵轴为反归一化后的股票收盘价格。

Fig.4 Forecast of CSI 300图4 沪深300预测

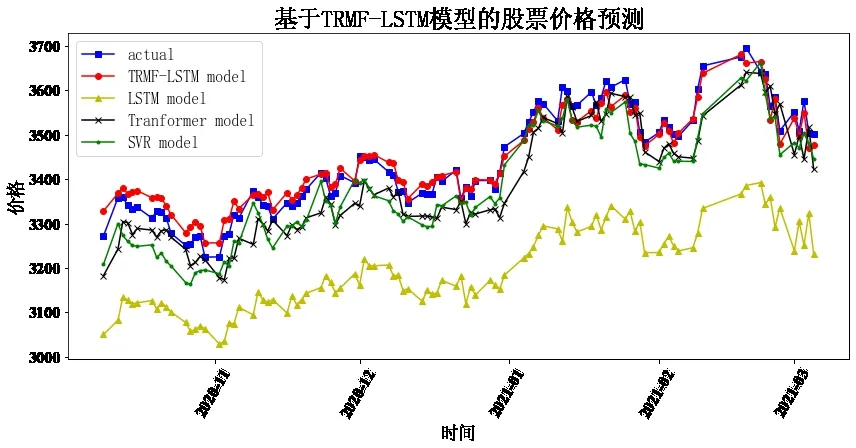
Fig.5 Forecast of Shanghai Composite Index图5 上证指数预测

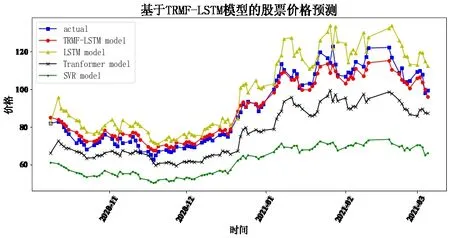
Fig.6 Forecast of Longi's图6 隆基股份预测

Fig.7 Forecast of Midea Group's图7 美的集团预测

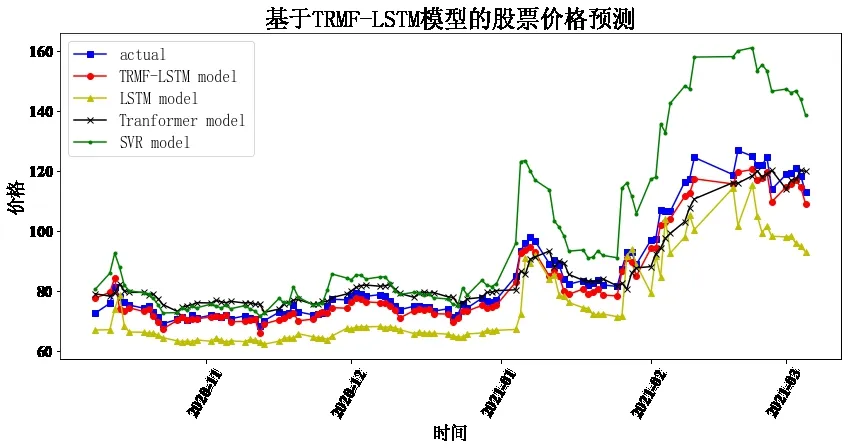
Fig.8 Forecast of Muyuan Stock图8 牧原股份预测

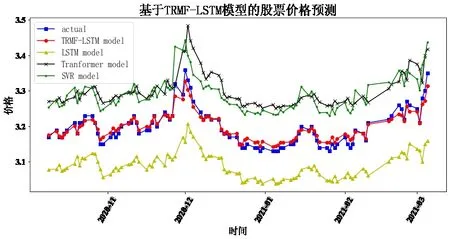
Fig.9 Forecast of Agricultural Bank of China图9 农业银行预测

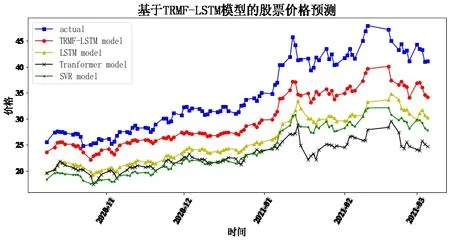
Fig.10 Forecast of Sany Heavy Industry图10 三一重工预测

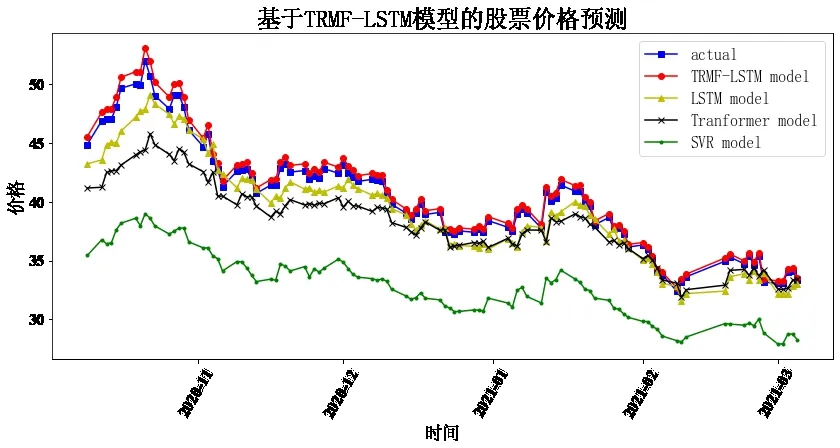
Fig.11 Forecast of China Life Insurance图11 中国人寿预测

通过8 只股票预测结果对比可以发现，LSTM、TRMFLSTM 和Transformer 相较于传统机器学习SVR 均与真实值较为接近，预测趋势基本保持一致，说明深度学习相较于传统机器学习在股价预测上具有较大优势。而相较于上证指数、隆基股份、牧原股份、农业银行与中国人寿五支股票，TRMF-LSTM 的预测结果明显最接近真实值，其余股票中，本文构建的模型相较于对比模型，对股价趋势预测有更高的水准，说明了本文组合预测模型的有效性，体现了线性与非线性预测方法相结合的优势。

为更好地观察对比效果并进行分析，计算每支股票每个模型预测的两类误差指标RMSE 和MAPE，并在8 支股票中取平均，如表1所示。

Table 1 Average evaluation index of stock price forecast表1 股价预测平均评价指标

可以看出，MAPE 和RMSE 的最小值均落在TRMFLSTM 组合预测模型中，Transformer 排在第二，LSTM 次之，SVR 排在最后。由此说明，本文构建的模型预测相较于对比模型更精准，也更好地验证了该模型能兼顾线性与非线性趋势。

4 结语

本文通过结合时序矩阵分解（TRMF）技术与LSTM 模型结合，构建TRMF-LSTM 组合预测模型，从而兼顾时间序列预测的线性与非线性部分。使用TRMF技术对股票数据集进行降维处理，并对线性部分进行拟合；然后将真实值与线性拟合值作差计算出残差，再利用LSTM 模型对残差进行训练，对数据的非线性部分进行拟合；最后将预测结果相加，得到新的组合预测值。该模型在选取的8 支股票预测中均取得了不错效果，相较于对比模型有着更低的误差，验证了模型的有效性。

本文将构建的模型应用于股票数据集，以第二日收盘价作为预测标签。考虑将该模型应用于其他数据集（如交通数据集），并利用多维时间序列的时间自相关性与因子相关性高精度预测多个标签，作为进一步研究的重点。