墩柱壅水数值模拟研究

董耀华，杨元平

(1.中水东北勘测设计研究有限责任公司，长春 130021； 2.浙江省水利河口研究院，杭州 310020)

墩柱壅水[1]计算是桥梁设计的重要内容，也是防洪影响评价的核心任务[2-3]。在桥梁水力计算中，除天然水流与自然河床外，总是以墩柱壅水计算作为主要内容[4]，因此墩柱壅水计算有着重要的实际意义。

近些年来，数值模拟逐渐成为墩柱壅水问题研究的重要手段[5-10]。而在数值模拟中，计算参数对于模拟准确性有重要影响，特别是紊动黏性系数(eddy viscosity)与壅水高度密切相关[11]，但对紊动黏性系数的作用规律研究仍然不足。目前，在利用数值模拟分析桥墩壅水的研究中，通常选取率定的方式确定紊动黏性系数的取值[5,12-13]。该方法依赖实测壅水资料，当缺乏壅水资料时，模型的准确性也就难以保证。张玮[14]等探讨了紊动黏性系数3种取值方式对壅水计算的影响，结果表明3种方法均可以成功地进行壅水计算。

本文拟设计物理模型试验，并利用试验数据建立平面二维水动力数学模型，然后应用模型分析紊动黏性系数3种取值方法与壅水高度的敏感性关系，研究3种紊动黏性系数取值方法与壅水高度的各自的作用规律，研究成果可为墩柱壅水数值计算提供一定参考。

1 物理水槽试验

试验在浙江省河口海岸重点实验室中进行，见图1。

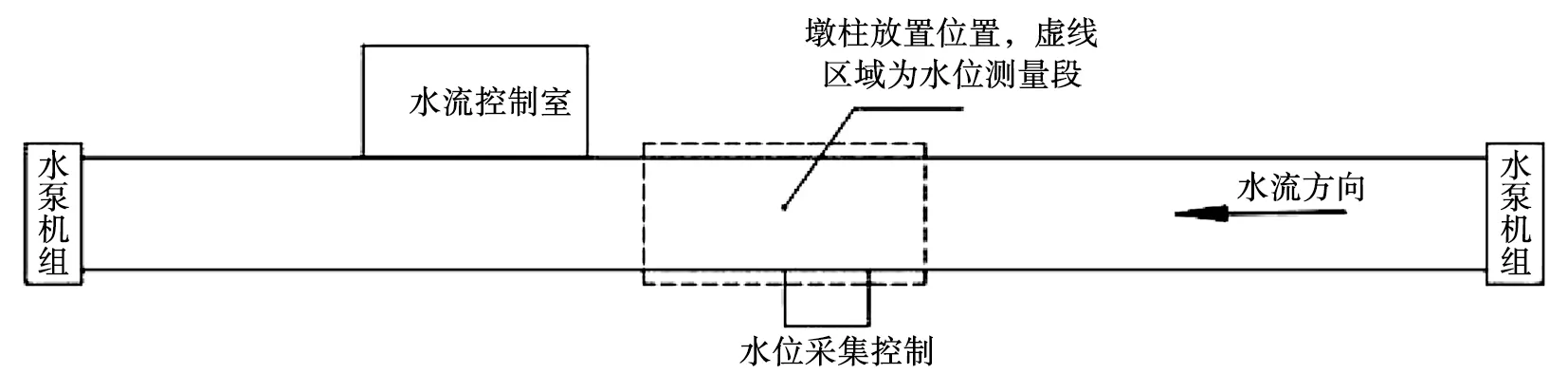
图1 水槽平面图

水槽为长50 m、宽4 m、高0.5 m的矩形平底水槽，水槽两端各有一组水泵，通过水流控制室的软件控制水泵的频率，可以调节水槽中水流的水位与流速；水槽中心位置放置直径11 cm圆柱形墩柱；水位测量采用超声波探头，精度为0.1 mm，探头固定在可向三维方向移动的高精度机床上，通过软件输入坐标，即可将探头移动至所需位置测量，水位测量装置及试验水槽局部见图2。此外，通过在墩柱上包裹细网格纸、利用相机拍摄墩柱淹没位置来测量墩柱前后水位差的方式，辅助观测壅水高度。

图2 水槽装置图

本试验共设计3组工况，见表1，均为恒定流。表1中，流速、水深为桩柱位置处的平均流速与水深。为获取壅水数据，每组工况均进行有墩柱、无墩柱放置两组试验。在图3中，以墩柱中心为坐标原点，对X轴上8个测点进行数据采集，通过计算有无墩柱试验数值差得到壅水数值；探头数据采集频率为20 Hz，考虑到水流的波动性，探头采集时间为1 min，取1 min数据平均值为采集结果值。

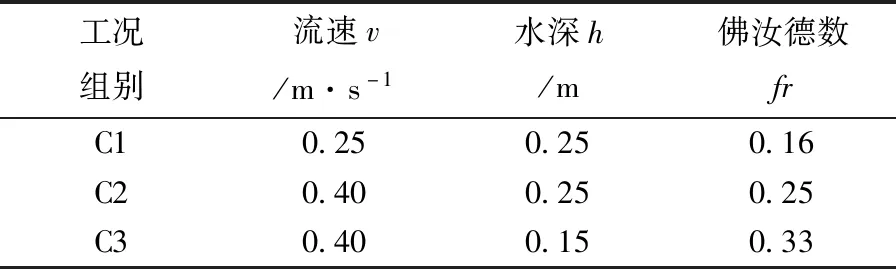
表1 物模试验水流条件

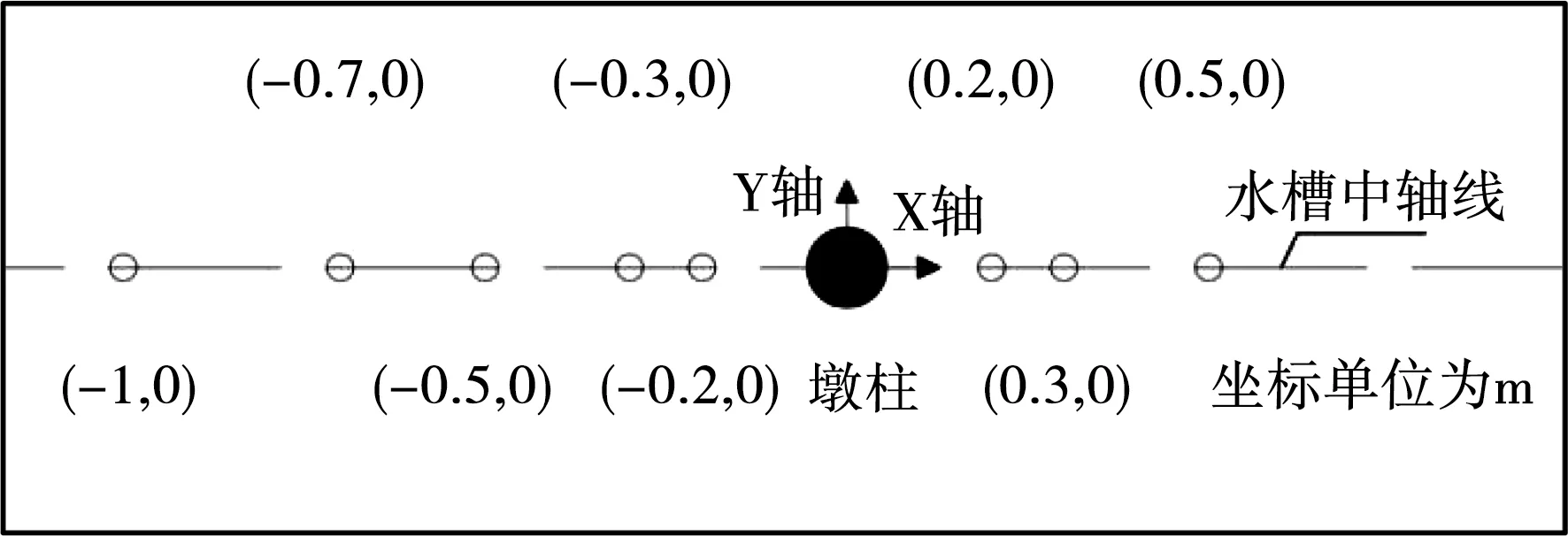
图3 测点位置图

试验结果见图4。考虑到测量误差及水位波动，壅水值有一定随机性，特别是远离墩柱位置处壅水值偏小的测点，波动较为明显，但整体变化规律仍十分清晰，可以作为数学模型验证的依据。

图4 壅水高度图

2 平面二维水流数学模型

2.1 控制方程与求解

应用SMS软件RMA2模块建立二维水流数学模型，RMA2模块的控制方程是将三维流动基本方程沿水深积分后平均得到如下方程组[6]。其中，式(1)为水流连续性方程，式(2)、式(3)分别为X、Y方向上的动量守恒方程。

(1)

(2)

(3)

式中：h为水深；u、v为X、Y方向的流速；x、y、t为直线坐标系和时间；ρ为流体密度；E为紊动黏性系数，xx为X轴表明上的法线方向；g为重力加速度；α为底部标高；n为曼宁系数；ζ为风应力系数；vα为风速；Ψ为风向；w为地球角速度；φ为当地纬度。

模型的求解过程为：①通过导入地形信息文件或手动输入散点，生成计算网格；②根据地形复杂程度和流速梯度的大小，对网格的疏密性及部分节点进行调整；③将模型计算网格和控制条件导入RMA2计算模块，对控制方程进行时间与空间上的离散，时间离散采用差分法，空间离散采用有限元法，并采用伽辽金加权余量法把控制方程从偏微分方程组转变成代数方程组进行求解计算；④计算结果后处理，输出图文成果[15]。

2.2 网格划分

参照物模试验建立数学模型，水槽长50 m、宽4 m，圆柱形墩柱直径为0.11 m。墩柱位于水槽中心，墩柱及附近区域用三角形网格划分，其它区域按四边形网格划分，将墩柱作为不透水区域处理，网格单元数量为18 212，单元节点数量为40 973，最大网格尺度0.35 m，最小网格尺度为0.01 m。网格划分见图5。

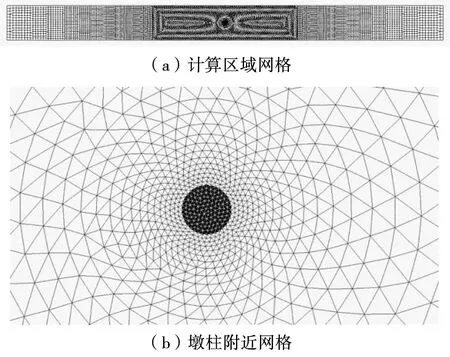
图5 网格划分情况

2.3 模型参数

曼宁糙率n与紊动黏性系数E取值对计算结果有重要影响[11]。糙率与水力坡度相关，根据实测比降率定得到糙率n为0.013。

紊动黏性系数E与壅水高度值有关。紊动黏性系数E定义为影响湍流交换的控制参数，而湍流(Turbulence)通常可以定义为速度随时间变化的影响，以及与其空间梯度相关的动量交换，是流体作不规则运动的一种流动状态。紊动黏性系数E的作用方程为：

(4)

(5)

(6)

(7)

式中：μ为分子黏度(Molecular viscosity)；u′、v′分别为X、Y方向的湍流速度波动。

紊动黏性系数E包括分子黏性力项和湍流速度波动项，但后者比前者大几个数量级，因此分子黏度通常被忽略。有3种基本方法可控制紊动黏性系数E，具体如下：

2.3.1 直接分配

按对应计算水流条件，直接为计算域分配E值。

2.3.2 按Peclet数分配

该方法允许模型在每次迭代后根据提供的Peclet数即P值自动调整E值。P值是基于每个元素内的唯一大小和计算出的速度，P值定义了平均元素速度值、元素长度、流体密度和E之间的关系，计算公式如下：

(8)

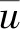
2.3.3 按Smagorinsky方程分配

该方法可以根据计算出的速度实时调整紊动黏性系数E值。相对于按Peclet数分配，它考虑了速度梯度，以确定合适的湍流系数来满足流体动力学模拟中的条件。Smagorinsky方程如下：

(9)

式中：TBFACT为方程系数；A为单元的面积；∂u/∂x和∂v/∂y为速度分量的变化率；E为紊动黏性系数。

2.4 边界条件

RMA2模型通过给定入口流量和出口水位设定边界条件。流量边界条件由物模试验墩柱位置流速乘以过水断面面积(水深乘以水槽宽度)计算得到；水位边界条件通过拟合物模试验墩柱位置的水深、流速率定得到。边界条件取值见表2。

表2 数模试验水流条件

2.5 模型验证与建立

确定数学模型的网格样式、边界条件设置、参数糙率值后，将紊动黏性系数以默认值设置，建立数学模型，并通过物理模型试验的壅水数据率定修正紊动黏性系数取值，最终数值模拟计算结果与对应紊动黏性系数取值见表3与图6。

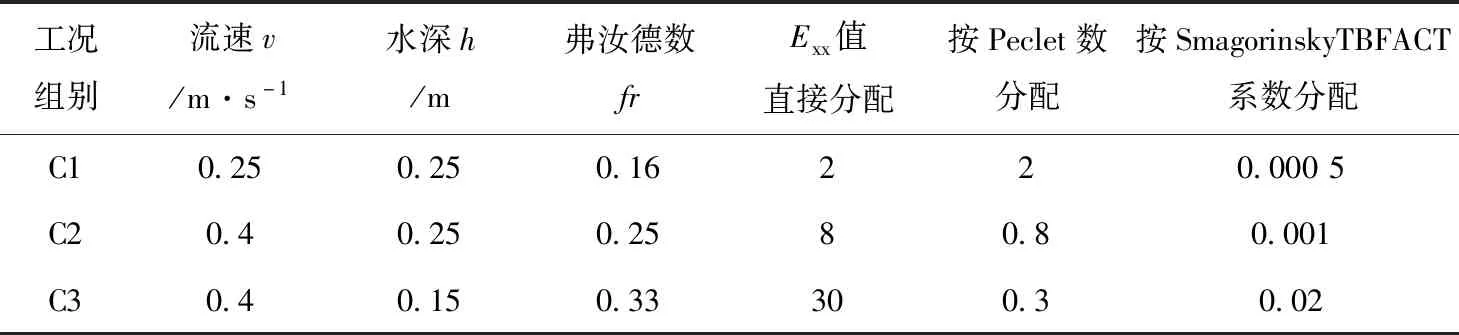
表3 紊动黏性系数取值

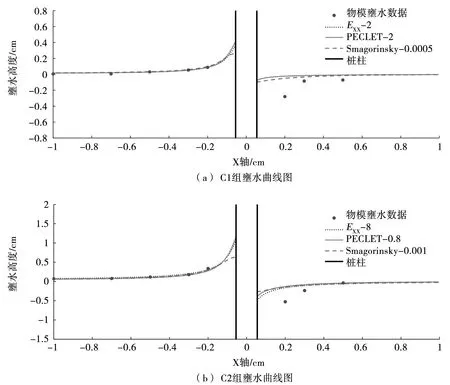
图6 各组壅水曲线图

由于物模试验墩后测点出现局部跌水,导致在流态上与数学模型存在差异[13],数值模拟时墩后水面下降模拟效果并不理想，故主要以墩前壅水验证紊动黏性系数取值。分析模拟结果，工况C1-工况C3的3种取值方法中，数学模型模拟壅水曲线与实测物模试验数据一致，数值模拟结果较为准确，可以认为表3的参数选取较为合理。此外，在靠近墩柱迎流测，按Smagorinsky方程分配的数模壅水曲线较另外两种方法结果低，水面线形态也与物模试验观察到的水面线形态接近。

3 紊动黏性系数敏感性分析

墩柱壅水数值模拟中，紊动黏性系数取值与壅水高度值密切相关。本节分析紊动黏性系数3种取值方法与壅水高度的敏感性关系，为紊动黏性系数的取值提供参考。

取工况C2进行数值模拟，在第2节数模结果基础上设计试验方案，分别研究3种紊动黏性系数方法取值与壅水高度的影响关系，方案设计见表4。其中，M8组方案为第二节工况C2数模紊动黏性系数取值。

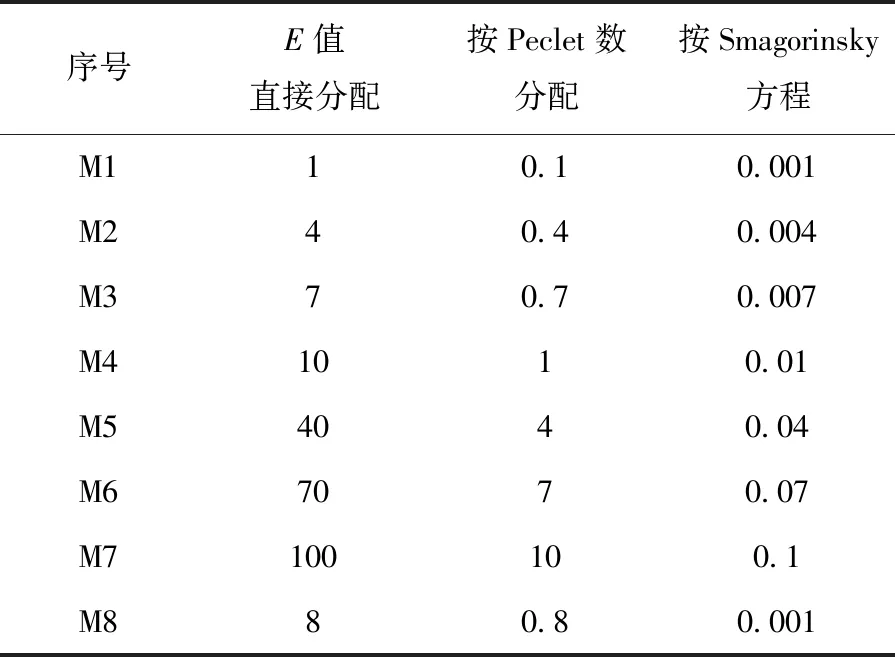
表4 敏感性分析方案

3.1 直接分配E值

图7(a)为数模计算结果生成壅水高度曲线图，图7(b)为数模计算生成的紊动黏性系数取不同值时的墩前各位置的壅水高度数据。由图7(a)可知，直接分配法中，壅水高度随E值增大而增大。由图7(b)中数据拟合可以得到E值与壅水高度的关系式(10)，并据此推出墩前各位置的壅水高度与E值之间具有明显的线性关系，即E值增加，壅水高度也按固定比例增加。

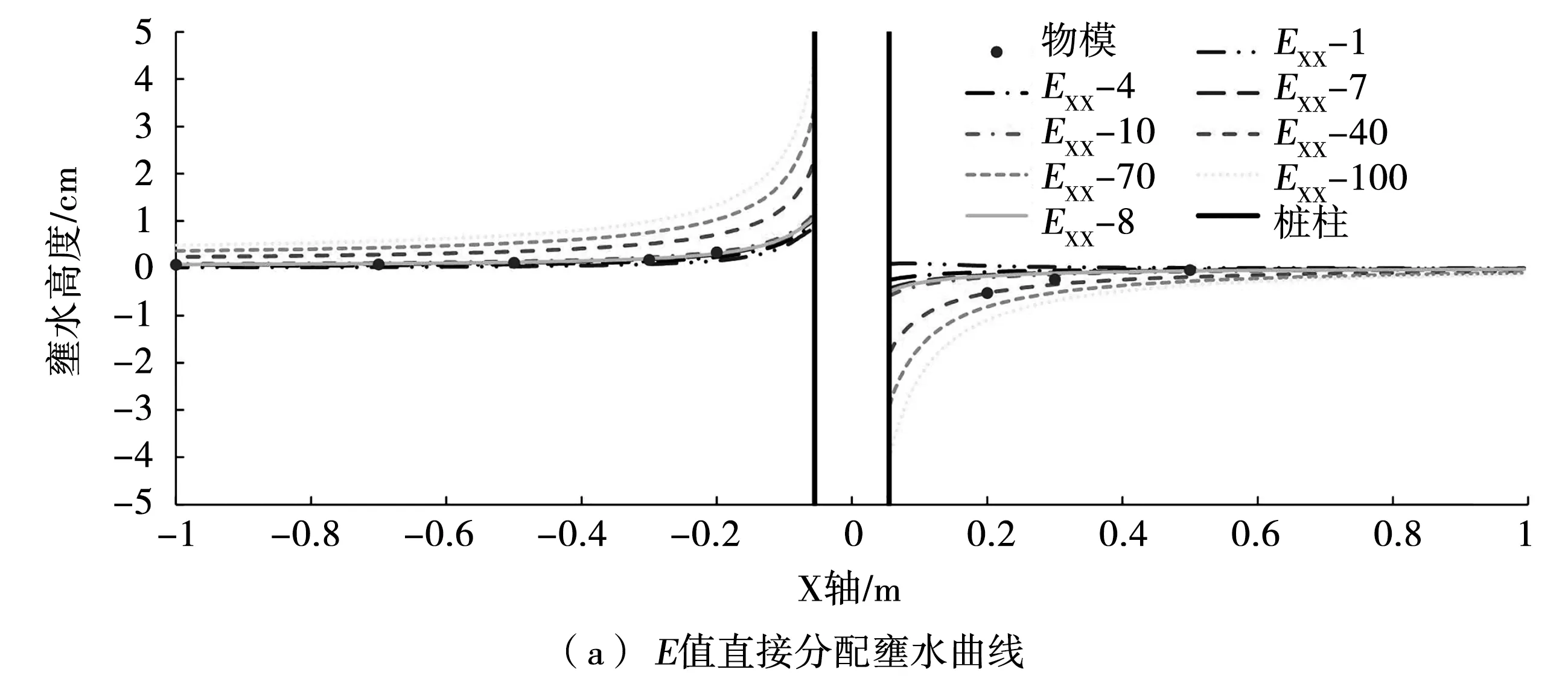
图7 E值直接分配结果分析

ΔZx=α1E+β1

(10)

式中：ΔZx为横坐标x处的壅水高度；α1、β1均为待定参数。

3.2 按Peclet数分配

图8(a)为数模计算结果生成壅水高度曲线图，图8(b)为数模计算生成的紊动黏性系数取不同值时的墩前各位置的壅水高度数据。由图8(a)可知，按Peclet数分配法中，壅水高度随P值增大而减小。由图8(b)中数据拟合可以得到P值与壅水高度的关系式(11)，并据此推出墩前各位置的壅水高度与P值间具有明显的乘幂关系，壅水高度随P值的增加而减小。当P趋近于0时，壅水高度大幅增加；随着P值增大，壅水高度的减小幅度逐渐趋缓。

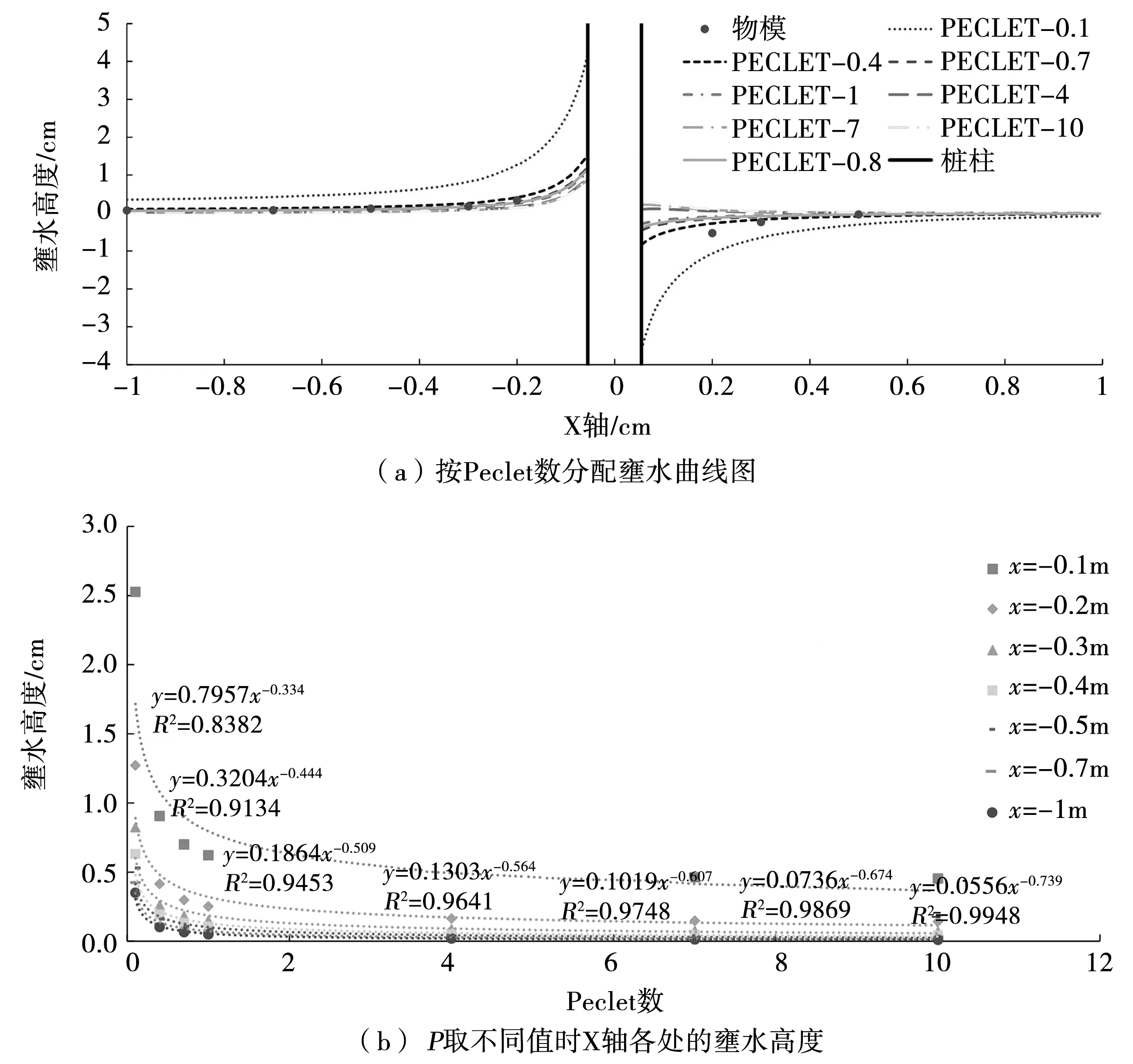
图8 按Peclet数分配结果分析

(11)

式中：α2、β2均为待定参数。

3.3 按Smagorinsky方程分配

图9为数模计算结果生成壅水高度曲线图，表5为数模计算生成的紊动黏性系数取不同值时墩前各位置的壅水高度数据。由图9可知，按Smagorinsky方程分配中，壅水高度随Smagorinsky系数增大而增大。为进一步分析表5，计算表5中相邻系数的壅水高度差值可知，壅水高度随Smagorinsky系数的增大而增加，但壅水高度的增加幅度随Smagorinsky系数增大逐渐减小。

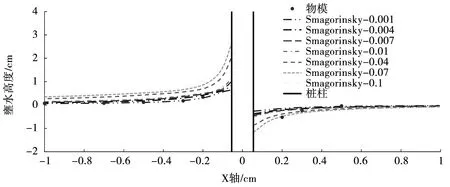
图9 按Smagorinsky方程分配壅水曲线图

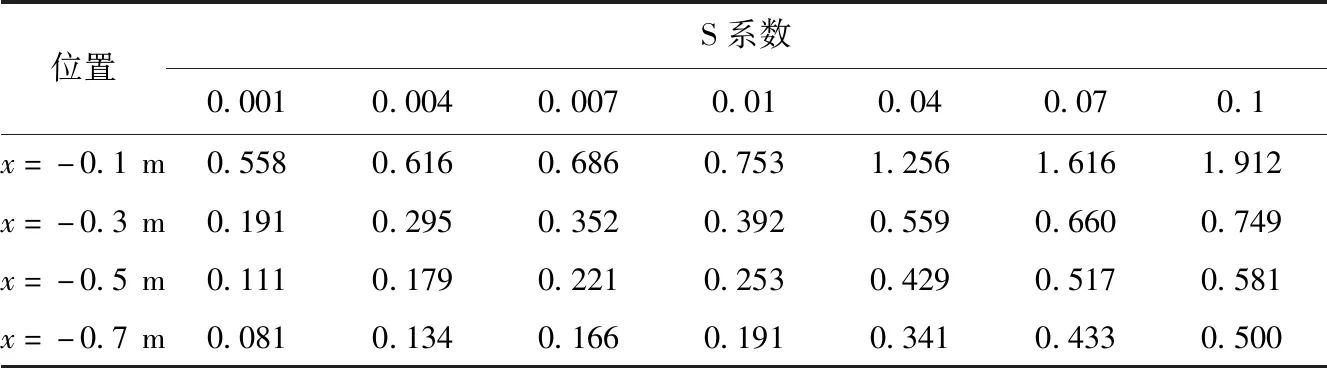
表5 Smagorinsky系数取不同值时中轴线各处的壅水高度 /cm

4 结论与展望

本文设计了墩柱壅水物理模型试验实测桩柱壅水，建立了描述墩柱壅水的平面二维水流模型，并应用该模型分析紊动黏性系数3种取值方法取值对壅水高度的影响。主要结论如下：紊动黏性系数的3种取值方式中，直接分配法中E值与壅水高度成线性关系，E值增加，壅水值以固定比例增加；按Peclet数分配法中P值与壅水高度成乘幂关系，壅水高度随P值的增加而减小，壅水高度的增加幅度随Smagorinsky系数增大逐渐减小；按Smagorinsky系数分配法中系数TBFACT与壅水高度无明显的函数关系，壅水高度随Smagorinsky系数TBFACT的增大而增加，但壅水高度的增加幅度随Smagorinsky系数TBFACT增大逐渐减小。

本文给出了紊动黏性系数3种取值方法与壅水高度的影响关系，在实际工作中，可以为紊动黏性系数的取值提供一定参考。