带有积分边值条件的分数阶微分方程组的正解

刘 洋, 李春红, 解大鹏

(1.合肥师范学院 数学与统计学院, 安徽 合肥 230601； 2.淮阴师范学院 学报编辑部, 江苏 淮安 223001)

0 引言

本文研究如下带有积分边值条件的分数阶微分方程组边值问题

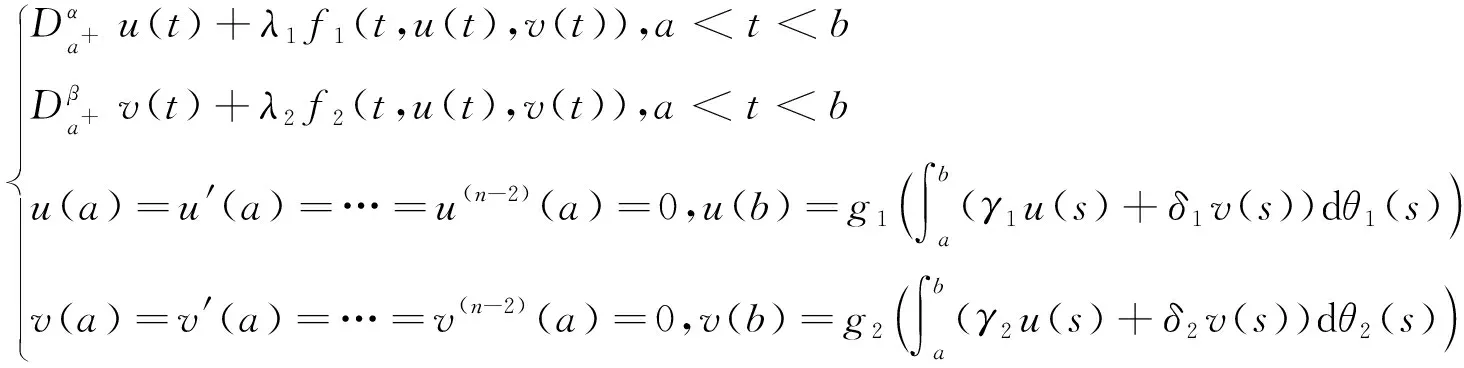
(1)

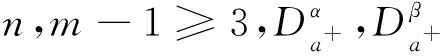
分数阶微分方程广泛地应用于流体力学、非牛顿力学等领域,有着重要的理论及实际意义.近年来,带有积分边值条件的分数阶微分方程组正解的存在性问题的研究,得到了丰富的结果[1-8].

令g1(t)=g2(t)=t,γ1=δ2=b=1,δ1=γ2=a=0,问题(1)可转化为如下问题

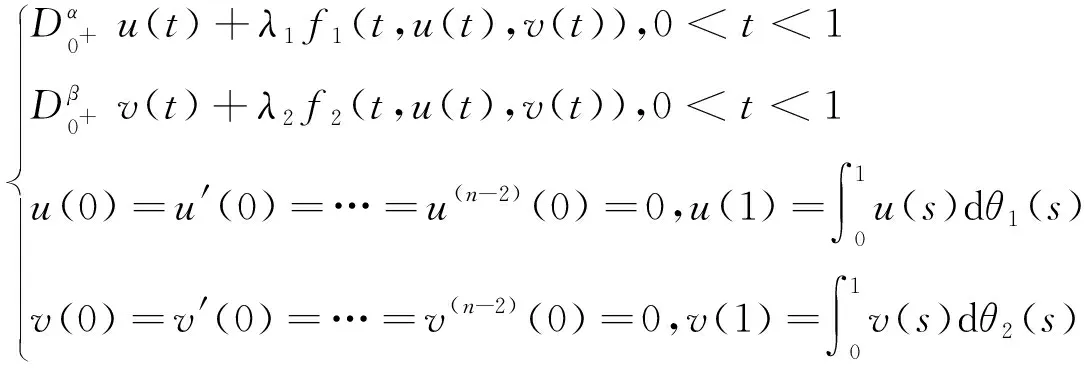
(2)

文[1-4]应用不动点定理得到了问题(2)正解的存在性.

令g1(t)=g2(t)=t,δ1=γ2=b=1,γ1=δ2=a=0,问题(1)可转化为如下问题

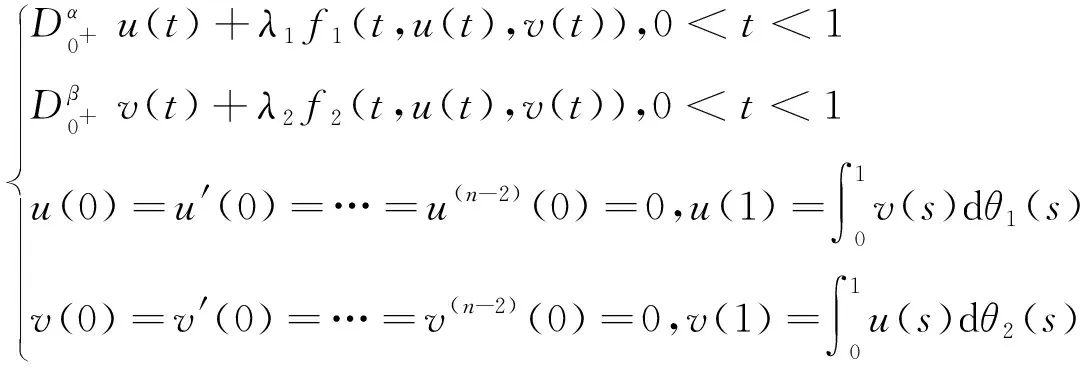
(3)

文[5-8]应用不动点定理得到了问题(2)正解的存在性.

受文[1-8]启发,本文将讨论问题(1)的正解的存在性,首先找到问题(1)对应的Green函数,并验证Green函数的性质,进而给出问题(1)的等价积分方程,最后,利用不动点定理得到了问题(1)正解的存在性.

1 预备知识和引理

引理1 设y∈C[a,b], 则边值问题

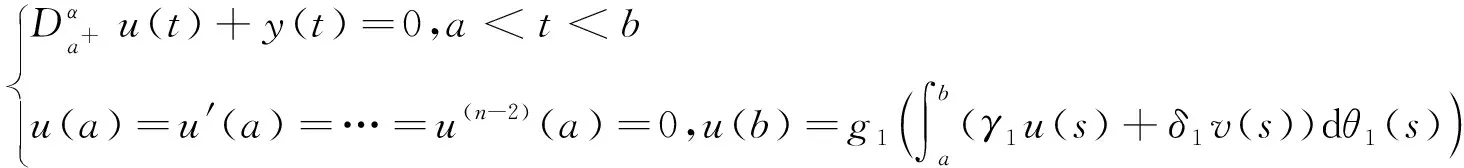
(4)

证明分数阶微分方程(4)的解等价于

由边值条件得,C2=C3=…Cn=0,且

所以

引理2 引理1中的函数G1(t,s)具有如下性质:

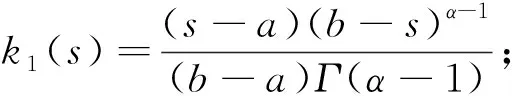
证明显然G1(t,s)≥0,(t,s)∈[a,b]×[a,b],当t≥s时,

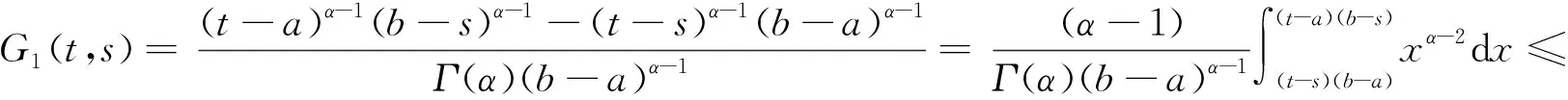
当t≤s时,

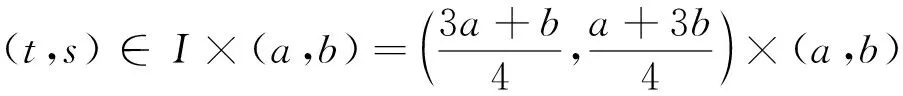
类同引理1及引理2,可得如下引理.

引理3 (i) 设y∈C[a,b], 则边值问题

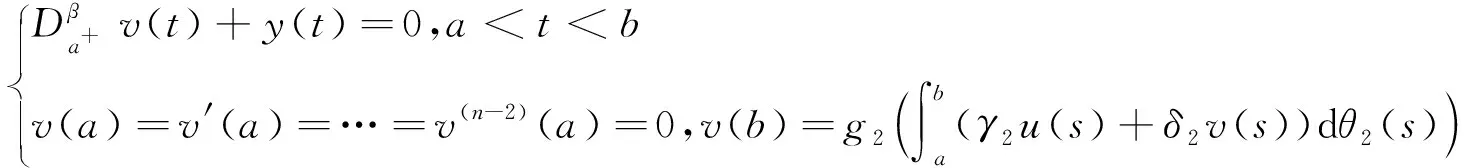
(5)

等价于积分方程

其中

(ii) 函数G2(t,s)具有下述性质:

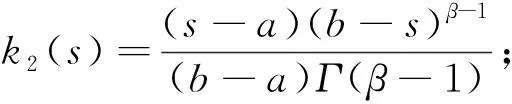
2 主要结果

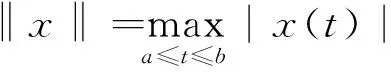
且K=K1×K2⊂E×E,下面定义算子Ti:Ki→E(i=1,2),

且定义算子T:E×E→E×E为

T(u,v)=(T1(u,v),T2(u,v)).

那么边值问题(1)有一个解当且仅当T有一个不动点.令

引理4 算子T:K→K是全连续的.

证明显然T:K→K是连续的.由引理2和引理3可得

上式说明T1(K)⊂K,同理可知T2(K)⊂K,所以T(K)⊂K.再由Arzela-Ascoli定理易得算子T:K→K是全连续的.

定理1 假设常数R>r>0满足如下条件，

则边值问题(1)至少存在一个正解.

证明令Ω1={(u,v)∈E×E:‖u‖≤r,‖v‖≤r}, 对于(u,v)∈∂Ω1, 由引理2和引理,及(H1)知,

故, 当(u,v)∈∂Ω1时,

‖T(u,v)‖*=‖T1(u,v)‖+‖T2(u,v)‖≥2r≥

‖u‖+‖v‖=‖(u,v)‖*,(u,v)∈K∩∂Ω1.

另一方面,令Ω2={(u,v)∈E×E:‖u‖≤R,‖v‖≤R},其中

R≥max{2g1(R(γ1+δ1)(θ1(b)-θ1(a))),2g2(R(γ2+δ2)(θ2(b)-θ2(a))),r}.

对于(u,v)∈∂Ω2, 由引理2、引理3及(H2)知,

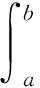
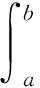
于是,当(u,v)∈∂Ω2时,‖Tu‖≤‖u‖.

‖T(u,v)‖*=‖T1(u,v)‖+‖T2(u,v)‖≤2R≤‖u‖+‖v‖=‖(u,v)‖*,(u,v)∈K∩∂Ω2.

综上,由不动点定理[9]知,边值问题(1)至少存在一个正解.(证毕)