接地线装置接触阻抗建模研究

叶青峰，肖拥东，刘瑞芳，李 洋，徐 杰

（1.国网安徽省电力有限公司亳州供电公司，安徽 亳州 236000；2.三峡大学，湖北 宜昌 443002）

0 引言

接地线装置是电力检修过程中确保工作人员安全的重要设备之一。接地线装置把电网检修部分与同大地等电位的接地体可靠连接起来[1]，可防止错误上电对检修人员的伤害。接地线装置中接地线与导线之间的接触电阻值的大小直观反映接地线装置的工作状况，接地线装置中接地线与导线之间是否可靠接触影响其接地保护的可靠性[2]。若接地线与导线之间接触电阻值过大，错误上电时导线电流不能快速流入大地，检修导线对地电位超过人体承受范围，将对人体造成伤害。

接地线装置通常由接地体、接地导引线、接地结构件和拟接地导线组成。接地结构件中的夹紧模块适度夹紧拟接地导线，使接地线装置中接地体与导线之间的接触电阻值在允许范围内，从而保证拟接地导线可靠接地。若接触电阻值较大，损耗增加，装置可能过热甚至烧毁[3]。因此接地线装置在投入使用前和使用过程中，对接触电阻的测试和实时监测很有必要。

接触电阻的传统分析方法一般忽略电感与电容效应，基于欧姆定律建立直流接触电阻模型。文献[4]针对母排接触所形成的接触电阻提出一种实时测量方法，通过采集母排连接处的电压差和流过连接处的电流，根据欧姆定律得到接触电阻。文献[5]采用脉冲大电流测量触点的接触电阻，得到较大的接触压降，并降低了电流引起的温升对接触面的影响，实现了接触电阻的精准测量。由于文献[5]只考虑电阻，测体必须是无感性和无容性的纯电阻性元件。文献[6]从影响接触电阻的因素和接触电阻的微观模型出发，介绍了最新的接触电阻模型和理论计算公式，提出在多点接触和频率提高的情况下，仅用接触电阻这一个参数不能很好地描述电接触模型，需要研究电接触的阻抗模型。文献[7]针对粗糙导体表面的电接触问题，建立粗糙表面的几何模型来研究两粗糙导体接触面的接触电阻和外加电压时粗糙面的电势分布，得出接触应力与接触电特性的关系，但该研究也只是局限于接触面的接触电阻，并未提出其他的电特性。

电力导线传输含有高频谐波的交流电，因此直接采用直流接触电阻模型来研究接地线装置中的接触阻抗并不恰当。本文建立考虑电容效应的接地线装置接触阻抗模型，采用注入谐振法实时检测接地线装置接触阻抗，并控制其在允许范围内。

1 接地线装置接触阻抗分析

图1为接地线装置挂接拟接地导线的示意图。由图可见，接地线装置的接触阻抗包括接地导引线、接地结构件等的体阻抗，以及夹紧模块与所压夹导线表面接触形成的接触阻抗。接触阻抗与两导体交错距离及其电接触面特性有关，而交错距离不仅受两导体间压力的影响，也会受导体界面延展形变性能的影响，因此两导体电接触面的微观状况是影响接触阻抗的关键因素。

电力行业实践应用中，由于交流电源工频为50 Hz，为便于分析和计算，可忽略接地感抗和容抗。这种接地线装置的经验模型将拟接地导线与接地线装置的电接触形成的阻抗简化为纯电阻，接地线装置的接触阻抗近似为装置体电阻Rt和接触面电阻Rj的串联，如图2所示。

2 夹紧模块和拟接地导线电接触面分析

实践工程中，由于制造工艺、接触面粗糙度以及结构件表面膜层的存在，接地结构件中的夹紧模块和拟接地导线之间并不是整面接触，其表面接触显微图如图3所示，图中d为两接触面参考平面的距离，r1和r2分别为两接触表面的顶峰高度。由图可见，夹紧模块和拟接地导线间的接触界面凹凸不平。这种凹凸不平的界面导致两个导体之间的实际电接触面积变小，即接触不是整面接触，而是两个导体表面的微凸体之间的接触[8−10]。

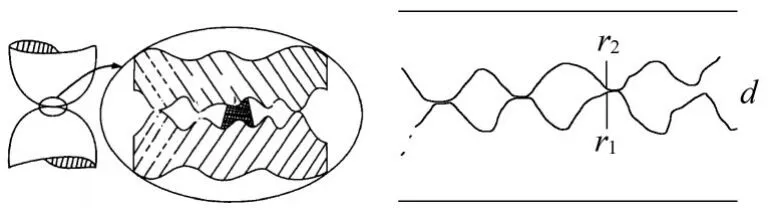
图3 夹紧模块和拟接地导线的表面接触显微图

两个导体之间的实际电接触方式有两种：一种是夹紧模块金属与拟接地导线金属之间的直接接触，电流通过这部分接触面时，电流线收缩形成直接接触电阻，也称为收缩电阻；另一种是两导体通过导体表面的具有一定导电性的污秽薄膜进行接触，这种经污秽薄膜进行的间接电接触会形成间接接触阻抗，其中由于薄膜而形成的电阻和电容分别称为膜层电阻和膜层电容。因此，电接触面存在收缩电阻和膜层电阻以及电感和电容，即电接触面存在复合阻抗。

在交流电力系统电路中，不仅直接接触电阻起作用，同时间接接触甚至非接触形成的阻抗也会起作用，尤其是间接接触或不接触产生的电容效应对电路参数的影响随电源频率增大而增大。当拟接地导线带电经接地线装置形成回路时，间接接触阻抗中的容抗和感抗等电气参数会影响接地线的接地状态，因而接地线装置的接触阻抗需要考虑包括直接接触电阻和间接接触阻抗在内的阻抗参数[11]。

基于两紧密电接触导体相关理论，分析两导体紧密接触的微观界面的阻抗。两导体之间的直接电接触形成的等效电阻为Rzi，电流的收缩等现象使电流路径延长，产生电感效应，形成电感Lzi；经污秽薄膜间接接触会形成膜层电阻Rmi和膜层电容Cmi；其他的非直接接触面即接触面空隙则会形成接触电容Cni。按照上述方法建立的夹紧模块与拟接地导线电接触面阻抗等效模型如图4所示。

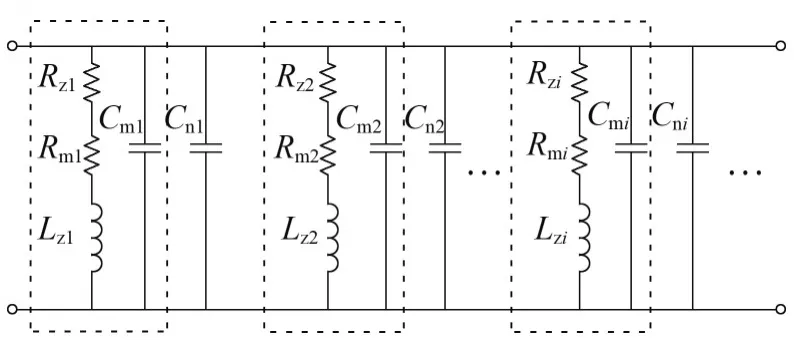
图4 夹紧模块与拟接地导线电接触面阻抗等效模型

3 接地线装置阻抗模型及参数计算

根据图4所示的夹紧模块与拟接地导线电接触面阻抗等效模型，可知总的等效接触阻抗为每个接触点和空隙形成的等效阻抗的并联。对每个接触点i（i=1，2，…，N），Rzi和Rmi串联构成接触点i的等效电阻，再与Lzi串联，形成RL串联等效支路；RL支路并联膜层电容Cmi和空隙电容Cni，即为每个接触点和邻近空隙的等效阻抗。所有接触点等效阻抗并联构成接触面的总等效阻抗。所有的膜层电容Cmi和空隙电容Cni并联等效成总的等效电容C。接触面的总等效阻抗由总的等效接触面电阻Rj与等效电感Lz串联，再并联总的等效电容C。当每一个接触点的等效电感Lzi很小时，可认为总的等效接触面电阻Rj为各接触点等效并联电阻。接地线装置等效接触阻抗为接地线装置体电阻Rt与上述电接触面等效阻抗的串联，如图5所示。

图5 接地线装置等效接触阻抗模型

依据有关电路定律，有：

式中：Gj为Rj对应的电导；Rzi和Rmi分别为接触点i的接触电阻和膜层电阻。

实际电接触形成的等效总电阻Rz为：

式中：ρ为接触材料电阻率；N和r分别为接触面处接触点的总数目和平均半径。

膜层等效总电阻Rm为：

式中：σ为膜层隧道电阻率；Ar为金属−膜层−金属接触区域的总面积。

并联总电容C计算如下：

式中：Cmi和Cni分别为接触点i的膜层电容和邻近空隙的空隙电容。

忽略边缘效应，两导体经污秽薄膜接触形成的等效电容与非接触空隙等效电容可以参考平板电容的计算方法：

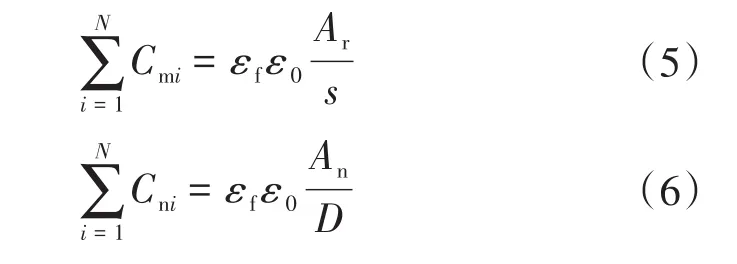
式中：εf和ε0分别为膜层介电常数和空气介电常数；An为非接触面积；s为界面间膜层的平均厚度；D为两接触面空隙的平均距离。

根据图3，基于统计特性对总并联电容C进行分析计算。通常情况下接触面存在按高斯函数分布的表面粗糙度高度。r1和r2分别为两接触表面的顶峰高度，高度ϕ1（r1）和ϕ2（r2）为相互独立的概率密度函数，则：

式中：σr1和σr2为高斯分布函数的标准差；mr1和mr2为高斯分布函数的平均值。

界面形成的微观峰顶的接触概率函数为W（x），则有：

式中：d为两接触面参考平面的距离。

如果接触面的接触视在面积设为A0，则膜层电阻可由下式计算得到：

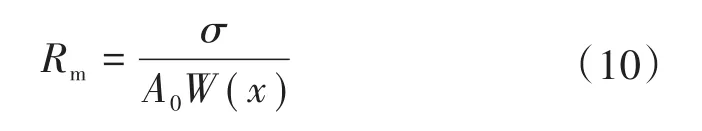
假设接触面的膜层均匀，厚度为t，则有：

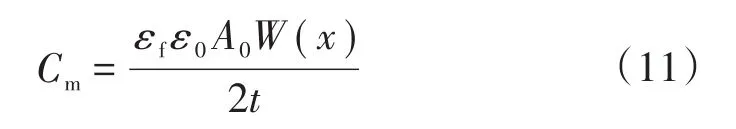
对于非接触电容Cn，其导电介质包括膜层和空气，其计算公式为：

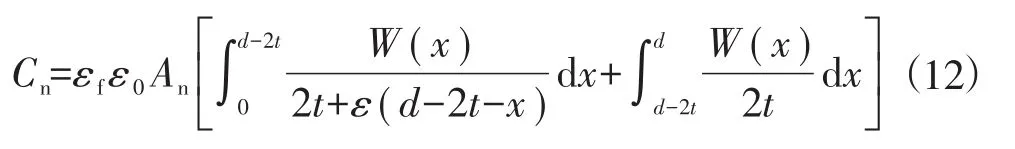
接地线装置总等效接触阻抗为：

供电导线长期暴露于空气中，导体表面会被氧化，因此两导体面接触电阻主要为膜层电阻，收缩电阻可忽略不计。同时，两导体面接触点为多点并联，电接触连接的长度有限，触点路径相对于大回路而言可以忽略，从而极大削弱了电感效应，可忽略电感。基于上述考虑，对模型进一步修正。修正后的模型如图6所示。

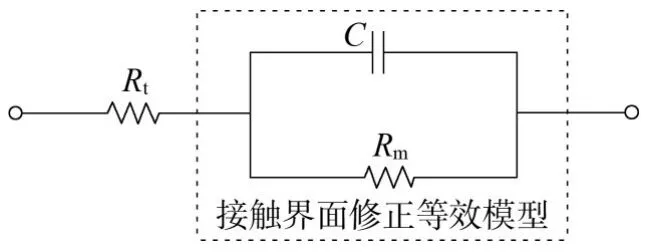
图6 接地线装置等效接触阻抗修正模型

接地线装置总等效接触阻抗可简化计算如下：

将某平口式接地线装置挂接在长期暴露于室外环境的导线上，采用LCR测试仪测试接触阻抗，验证所提模型。多次测量后取平均值，得出电阻值为50.03 mΩ，电容值为8.96×10−11F，验证了所提接地线装置的RC并联接触阻抗模型的合理性。

4 结语

本文基于接地线装置中夹紧模块与拟接地导线两个导体的接触面微观状态电参数，分析接地线装置电接触面总阻抗，从而建立含有电阻、电容、电感的等效电路模型。根据实际需求和各参数权重，进行简化修正，得到接地线装置的RC接触阻抗模型，并从统计特性的角度推导出RC接触阻抗模型中各阻抗分量的计算公式。