加速运输试验中非高斯振动响应疲劳损伤等效
2022-09-22朱学旺范庆辉宁佐贵程家军
朱学旺,范庆辉,宁佐贵,程家军
(中国工程物理研究院总体工程研究所,绵阳 621900)
引言
加速试验是研究装备运输环境适应性的一种主要的技术手段,其理论依据是线性疲劳损伤累计理论[1-5]。这种方法通过提高激励载荷量级并缩短试验时间,实现对被试装备施加等效的疲劳损伤考核。GJB 150.16A-2009《军用装备实验室环境试验方法——振动试验》和MILSTD-810系列标准(ENVIRONMENTAL ENGINEERING CONSIDERATIONS AND LABORATORY TESTS,MILSTD-810F、MIL-STD-810G、MIL-STD-810H等)都提供了具体的加速因子计算方法[6-9]。
这种加速运输试验方法所适用的对象是高斯随机振动作用下的线性时不变系统(LTI)。 当激励是非高斯随机振动时,LTI系统的响应也是非高斯随机振动[10],此时的疲劳损伤就不适合于传统的估计方法。采用传统的加速试验方法时需要考虑这种影响,国内外的试验标准提出了关注两种工况,即一是现场环境分析便发现了明显的超高斯随机振动,二是实验室加载时必须采用的CF(crest factor,限峰)技术会导致加载驱动信号本身便具有非高斯特征。当环境为超高斯时,可以采用激励为超高斯的新的试验方法[11,12]或者将超高斯激励谱转化为等效的高斯激励谱而采用传统加速试验方法[13];而CF的影响,一般认为,当CF≥3时,精度能够满足工程应用要求[14]。
还有一种情况,就是被试装备出现非线性时,即使加载是高斯振动或接近高斯振动(如控制器提供的经过CF后的亚高斯激励信号),装备的响应也会是超高斯随机振动。这种现象在加速运输试验中常有发生。如果不考虑超高斯振动的疲劳损伤影响,则可能导致过试验而失效。本文将局限于这类问题的讨论。
首先列举加速运输试验实测数据,确认被试装备响应超高斯特性的存在;然后介绍一种超高斯随机振动疲劳损伤的频域估计方法,并应用于疲劳损伤等效分析;接着将该方法应用于试验结果分析,给出一种基于非高斯振动响应疲劳损伤等效加速运输试验设计和分析方法,并给出计入疲劳损伤等效考虑的加速运输试验指标。
1 加速运输试验响应的超高斯特征
图1和图2为按照传统高斯随机振动设计并完成的2个加速运输试验响应控制结果。其中,图1(a)、图2(a)为控制谱(数值均进行了归一化处理)。不难发现,其控制精度都满足了规定的允差要求。按照条件规定的试验时间(T1和T2)完成加载,分解检查发现了被试装备损伤故障。图1(b)、图2(b)分别为一个控制点的加速度时间历程,可以检验,其偏度和峭度值分别为0.51、0.55、4.845和4.999,表现出明显的超高斯特征。偏度和峭度估计的数学表达式为公式(1)、(2)。
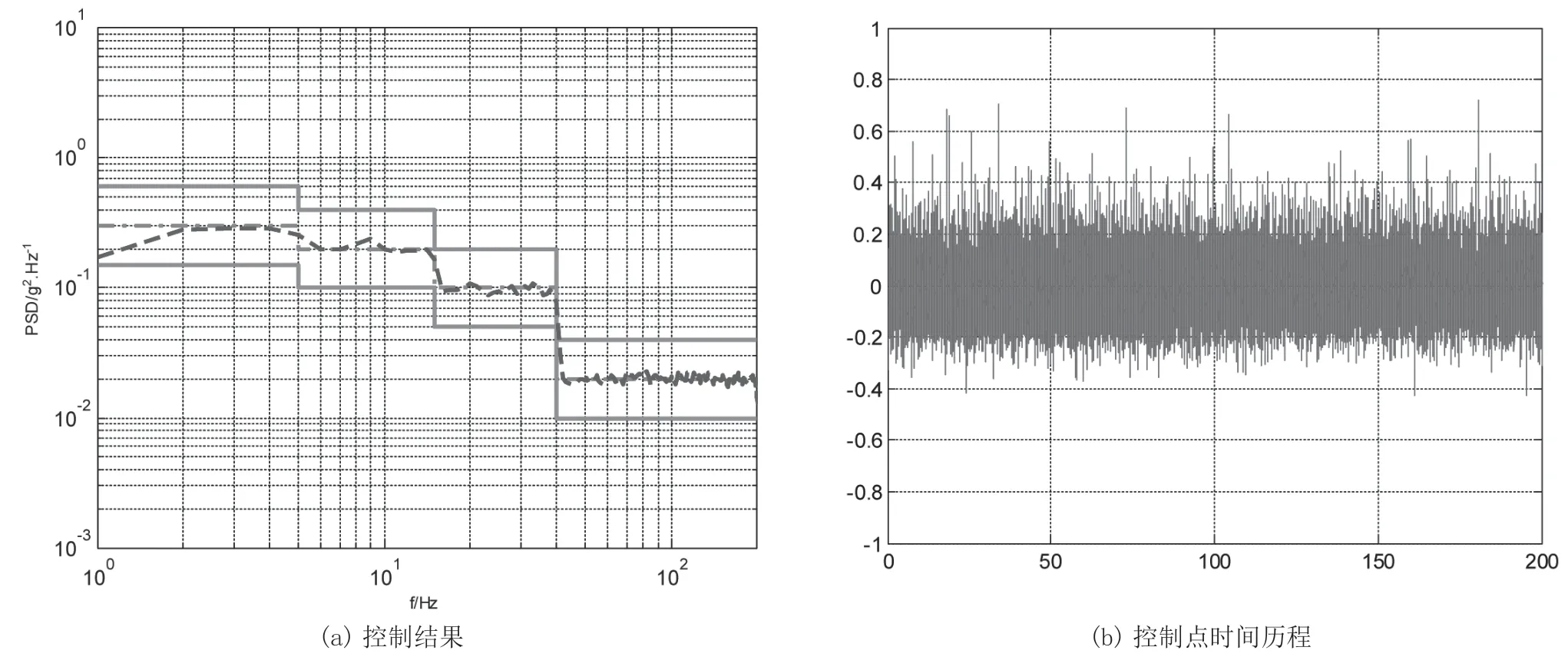
图1 试验1 实测数据
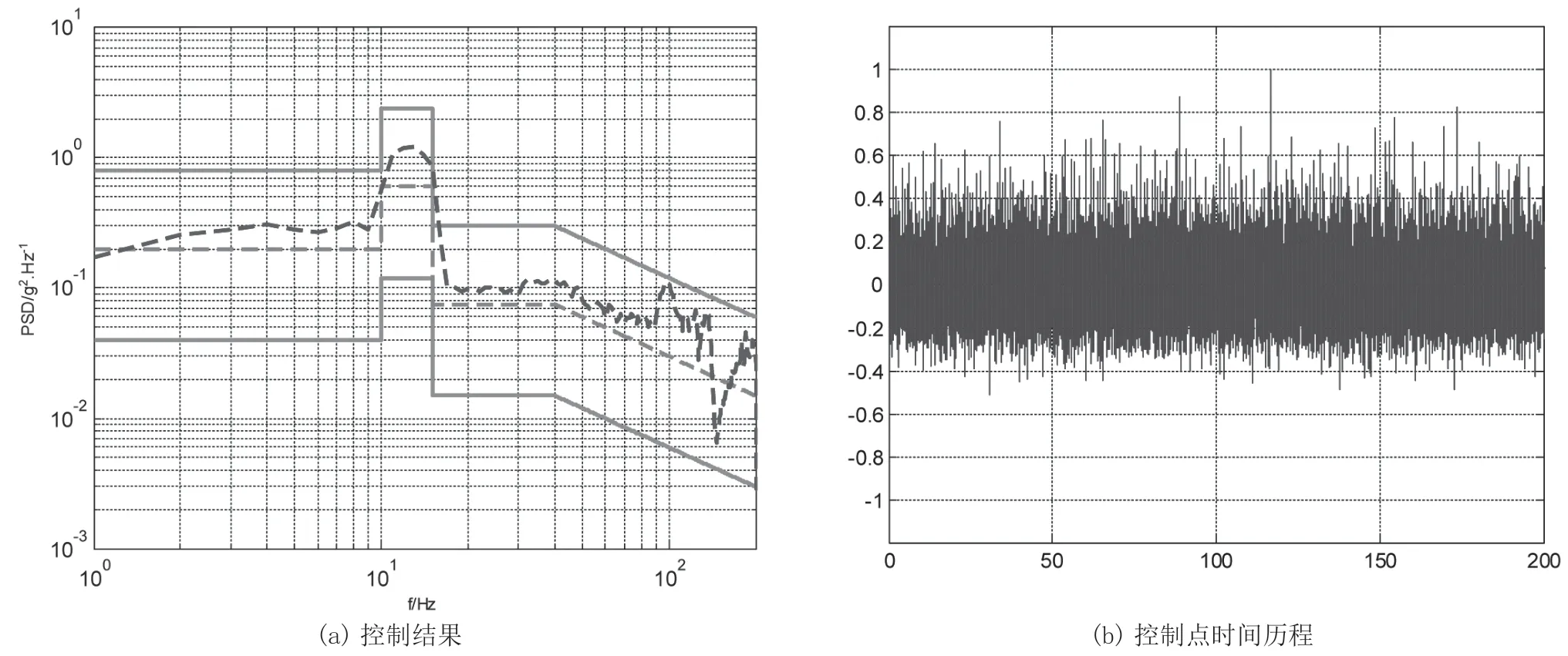
图2 试验2 实测数据
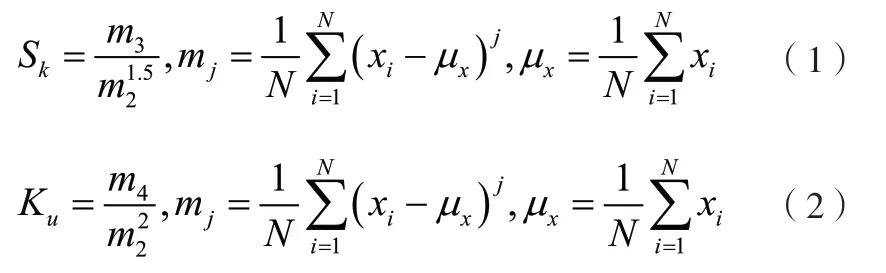
可以确认,控制器给出的驱动信号是近似高斯的,尽管采用了峰值限制技术对驱动信号的峰值进行限制(CF=3),但是其峭度值接近3(实测结果为2.91),图3是其概率分布结果。不难判定激励并没有提供超高斯的大峰值输入,严格说是亚高斯的。造成响应出现超高斯特征的原因是被试装备结构的非线性所致。因为线性系统在随机振动激励作用下的响应统计特征具有传递性,即激励是高斯则响应也是高斯,激励为超高斯,响应也是超高斯,激励是亚高斯,响应也是亚高斯。LTI系统随机振动峭度的传递可以用公式(3)定量描述[10]。
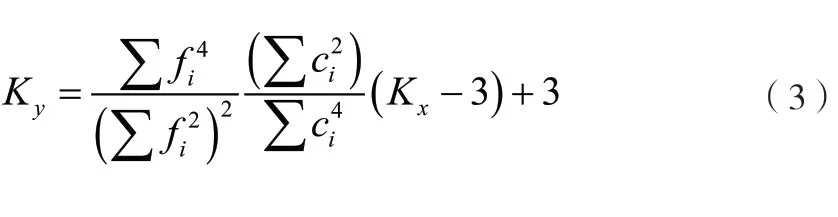
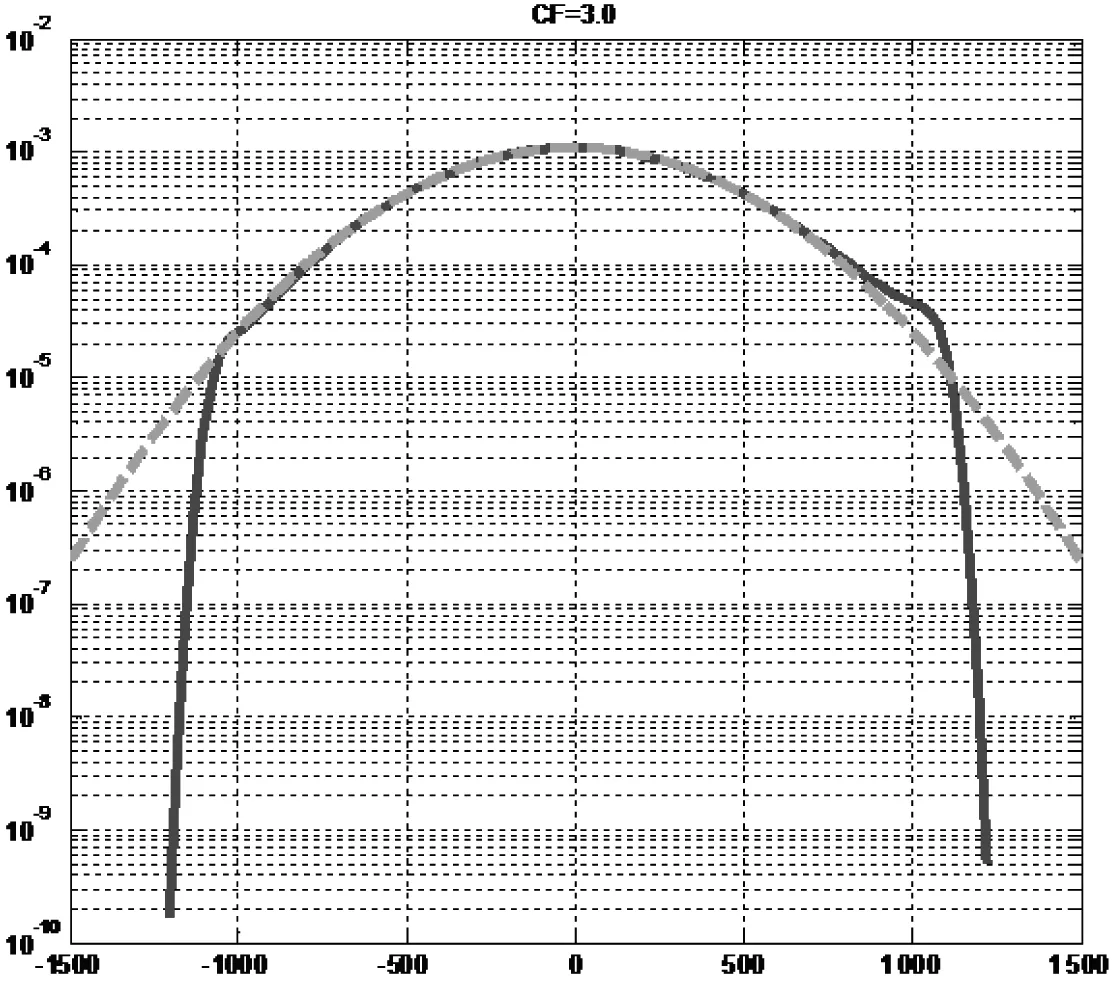
图3 试验1 驱动信号概率分布曲线
式中:
K y、Kx—响应和激励信号的峭度;
fi和ci—激励信号自相关函数与脉冲响应函数的卷积和激励信号自相关函数值。
2 一种频域疲劳估计方法
如果不顾及非线性导致的响应信号的超高斯特征,而按照预先设计的试验时间加载,则必然造成过试验,因为初始的试验设计是基于高斯加速试验方法的,而超高斯随机振动响应具有更大的疲劳损伤能力。
非高斯随机振动的疲劳损伤估计仍然是开放的研究领域,尽管时域估计方法如雨滴计数法等可以获得满意的结果,但是这类方法因为需要具有统计意义的载荷原始数据而难以实现工程应用界。需求简单快捷的频域方法是业内同行的共同目标。
Benasciutti,R.Tovo应用联合概率分布函数得出了一种可估计非高斯随机振动疲劳损伤的方法[15],Jie Ding,Xin-zhong Chen等人采用联合概率密度函数守恒,也提出了一种类似的疲劳损伤估计方法[16,17]。这类方法尽管称之为频域方法,但是需要应用到时域信号的非线性变换,还是没有回避需要具有统计意义的载荷这一难题。文献[18]介绍一种简单的超高斯疲劳损伤估计方法,他在总结前人研究[19,20]的基础上,提出了一种不考虑RMS影响的非高斯疲劳损伤等效因子数学表达式,将非高斯载荷与具有相同PSD的高斯载荷的疲劳损伤表述为与峭度、偏度和材料参数相关的量,如公式(4)所示:
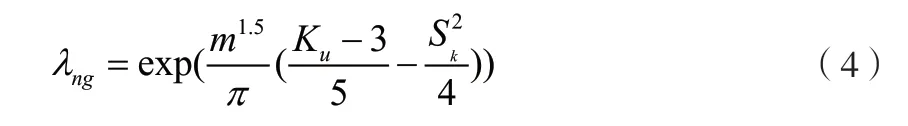
本文依据公式(4)来建立疲劳损伤等效关系。这样具有相同PSD的高斯振动和非高斯振动在相同时间作用下的疲劳损伤定量关系为:
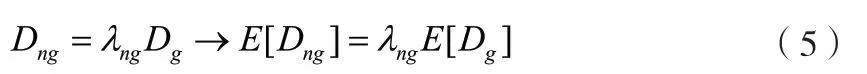
式中:
Dng、Dg、E[Dg]、E[Dng]—非高斯与高斯振动的疲劳损伤与期望疲劳损伤。
根据公式(5)便可以实现对上述试验进行设计修正,以避免过试验的发生。
3 考虑响应非高斯特征的加速试验方法
为了避免超高斯响应对试验装备的过试验考核,需要对加速试验设计进行修正。可以缩短试验时间或降低试验量级来实现。前面分析表明,响应的非高斯特征是由于装备结构的非线性引起,而结构的非线性与载荷量级密切相关,降低试验量级可能改变响应特征,故本文仅从缩短试验时间(试验量级不变)方面进行修正。
T根据疲劳损伤等效和公式(5),不难导出:

式中:
Tn g,T—考虑非高斯影响的经修正的试验时间和原设计试验时间;
ngλ—公式(4)给出的等效因子。
以下针对上述两个加速运输试验实测数据进行试验修正。试验1和试验2的原设计时间分别为50 min和45 min。由于控制点的响应加速度信号表现出明显的超高斯特征,必须缩短试验时间才能够避免过试验。
表1列出了2个试验的4个控制点的偏度和峭度估计结果,以算术平均值作为等效因子计算的参数取值,不同材料疲劳参数(3~9)时等效因子变化见图4。

表1 加速度运输试验控制点非高斯参量估计结果
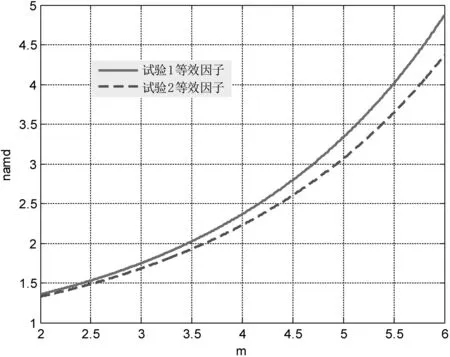
图4 等效因子随材料疲劳参数变化
材料疲劳参数若按文献1推荐的4考虑,则等效因子分别为2.368、2.223,实际修正的试验等效时间为21.1 min和20.2 min。
4 结论与讨论
文中应用非高斯疲劳损伤等效因子方法,对两个典型的加速运输试验进行了等效修正,在不改变控制方式和控制谱的情况下,因为响应出现了超高斯特征而强化了试验件的损伤,需要缩短试验时间,材料疲劳参数为4时,试验时间分别由原先设计的50 min和45 min修正为21.1 min和20.2。类似地,可以针对试验件材料的不同构成,合理的选择材料疲劳参数,实现对出现超高斯响应的振动试验进行修正,以避免过试验的发生。
文中分析讨论没有计入控制器CF处理对结果的影响。趋势上,CF的作用会相对降低对试验件的考核,欣慰的是,CF=3时,这种降低不会影响工程研究的精度[14]。文中对2个试验控制点实测数据进行的偏度估计和峭度估计的样本长度约10的6次方,严格说来精度不够,一般希望达到7次方。但是,原始数据的长短并不影响方法的说明,且因为试验设计时间的限制,也可能不允许我们获得更长的数据样本。
