基于多标签模糊推理改进KNN家居老人定位算法研究
2022-09-22周绍军刘晓霞胡云冰
周绍军,刘晓霞,胡云冰
(1.四川水利职业技术学院信息工程学院,四川 崇州 611231;2.厦门大学信息学院,福建 厦门 361001)
1 引言
人口老龄化主要是由于新生儿数量降低和人类寿命延长所致,这就造成老年人口相对增加和人口结构呈现老年状态[1].我国已进入老年化社会,因60周岁及以上人口已占总人口的18.1%,而且65周岁及以上人口已占总人口的12.6%[2].又由于少子化因素,造成老人空巢于家中,由此,家居老人的看护正在成为亟待解决的社会问题.利用RFID(Radio Frequency Identification,RFID)技术对家居老人位置进行感知,通过通信技术传输给老人的监护人,实现远程实时动态感知与监护,从而解决无数家庭的忧烦.因此,研究RFID的家居老人定位是具有理论意义和现实意义的.
对老人看护方面,研究者们进行了诸多研究,有从身体体征[3]角度进行研究的,有从老人跌倒[4]角度进行研究的,也有从老人发生事故救援[5]角度进行研究的,还有对老年人HAR(Human Activity Recognition,HAR)和异常行为[6]进行研究等.随着大数据和物联网技术等的发展,越来越多的新技术应用于健康领域,如文献[7]和文献[8],对新技术在医疗健康领域应用进行了综述.文献[9]对基于计算机视觉的室内定位和导航进行了综述,阐述了利用行人推算方法和各种通信技术(如Wi-Fi、射频识别、可见光、蓝牙和超宽带等)的导航和定位方法等.在RFID定位方面,诸多研究者进行了研究,如文献[10]和文献[11],分别对RFID在室内定位和三维定位进行了研究;有对利用RFID对家居老人睡眠进行检测的[12],亦有利用RFID对人体坐姿进行研究的[13].以上研究成果,为进一步研究RFID技术应用于家居老人定位问题,提供了有益的参考.
综上,现有研究要么利用RFID于老人生命体征的健康监控,要么与其他算法结合实现定位,未专门针对可独立家居老人定位.因此,研究多标签家居老人定位算法,并进行实验与仿真分析,具有积极意义和实用性等.
2 系统模型
利用物联网RFID感知技术,对独立居家老人的家居位置进行感知,从而实现对家居老人的监护.
家居环境是一个小区域多点位的三维空间,利用多方位布置的RFID感知器,感知老人携带的多部位的多个RFID无源电子标签,示意图如图1所示.在居家老人的特制外套放置8个UHF(Ultra High Frequency,UHF)RFID标签,如图1所示.在室内固定位置Cogi(xgi,ygi,zgi)(i=1,2,…,n)安装多个UHF RFID阅读器,在固定时间间隔Tj(j=1,2,…,n)内轮流读取老人身上的标签信息,进行老人位置的数据采集.

图1 系统模型示意图Fig.1 Schematic Diagram of System Model
家居老人在家中某一位置的站立、坐椅子或蹲下,如图1的位置A、B、C所示.多个RFID阅读器同时读取位置A或B或C的UHF标签数据,得到家居老人的RFID标签位置指纹,通过与kNN(k-Nearest Neighbor,kNN)算法结合,建立老人定位机制,从而实现对家居老人定位,其具体示意图如图2所示.

图2 RFID标签指纹老人定位方法架构Fig.2 RFIDTag Fingerprint Elderly Positioning Method Architecture
依据图1待定位的老人携带的RFID标签,利用图2框架,通过固定位置安装的阅读器,读取标签数据,以标签到阅读器间的距离描述位置.利用采集得到的老人位置指纹,通过定位算法得到老人在家居中的具体位置.
3 定位算法
3.1 原理
阅读器Cogi(xgi,ygi,zgi)在固定时间段内,不间断发送UHF波,接收老人携带的RFID标签反射信号,若假设阅读器与标签间的空中直线距离为Lij(i,j=1,2,…,n),则阅读器收到标签信号之后解调得到的相位值为:
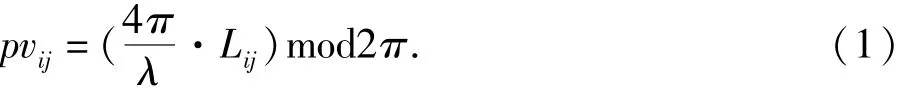
其中:λ为载波波长;mod(·)表示除取余运算;i,j=1,2,…,n.
由式(1)可知,在时刻t位置Cogi(xgi,ygi,zgi)的阅读器实际测得的相位值,理想情况下是没有误差,而由于多径效应和链路时延,实际值与理论值间存在误差,即,其中cpd表示由于标签和阅读器工艺、链路相位延迟等确定,不同阅读器和标签cpd值不同,cre为多径效应带来的随机误差.
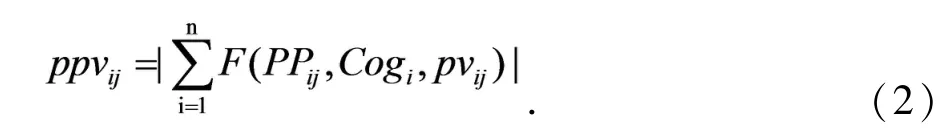
利用式(2)得到标签指纹,并结合房间RFID阅读器位置,得到老人携带标签位置,从而实现对老人的家居定位.
3.2 算法
采用三输入模糊推理系统与kNN结合算法,将三个关联参数作为算法的输入,输出位置估计值与后继kNN定位的计算值[14].其算法模型如图3所示.
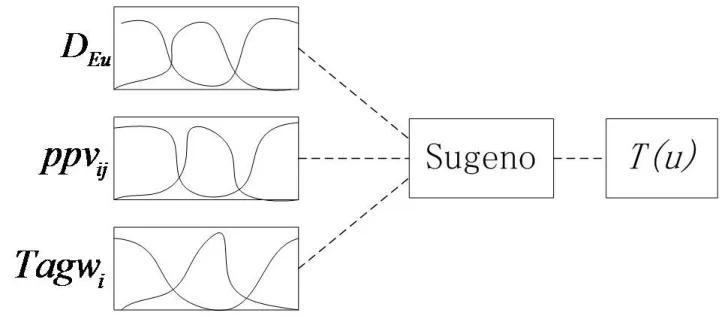
图3 改进模糊推理结构图Fig.3 Structure Diagram of Improved Fuzzy Reasoning
图3中,DEu表示待定位点与指纹库中的各个指纹的欧几里得距离,ppvij表示由式(2)确定的Tagi的像素值,Tagwi表示Tagi权重值.利用计算的欧几里得距离DEu,进行k个临近节点选择,使得DEu越小,则待定位点与此指纹节点的相似度就越大.
用kNN算法选定k个邻近指纹节点,按照式(2)求得ppvij,然后将ppvij按照转换为与阅读器Cogi(xgi,ygi,zgi)的距离Li.Li的计算式为:
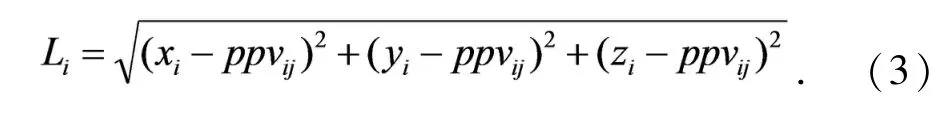
依据Sugeno原理,改进模糊推理规则如表1所示,其中VVH表示所得到的值很高很高,VH表示很高,M表示适中,L表示低,VL表示很低.
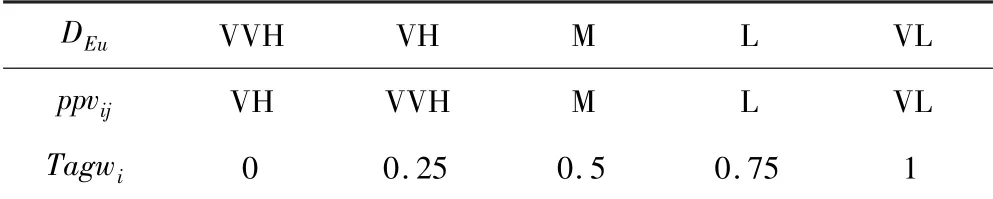
表1 模糊规则表Table 1 Fuzzy Rules
经过模糊规则库处理得到该事件发生概率,并将概率作为权重对kNN中的各个邻近节点进行加权处理,若DEu和ppvij的值越小,则赋予的权重值就越大.因此,得到待定位点的坐标为:
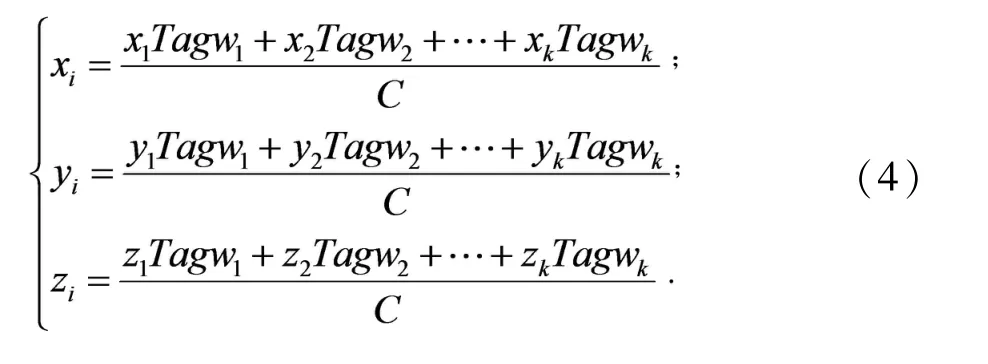
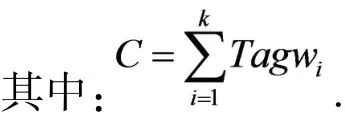
因此,得到模糊推理系统与kNN结合算法流程如图4所示,其中位置库为依据家居老人具体室内情况,建立的家居位置库.
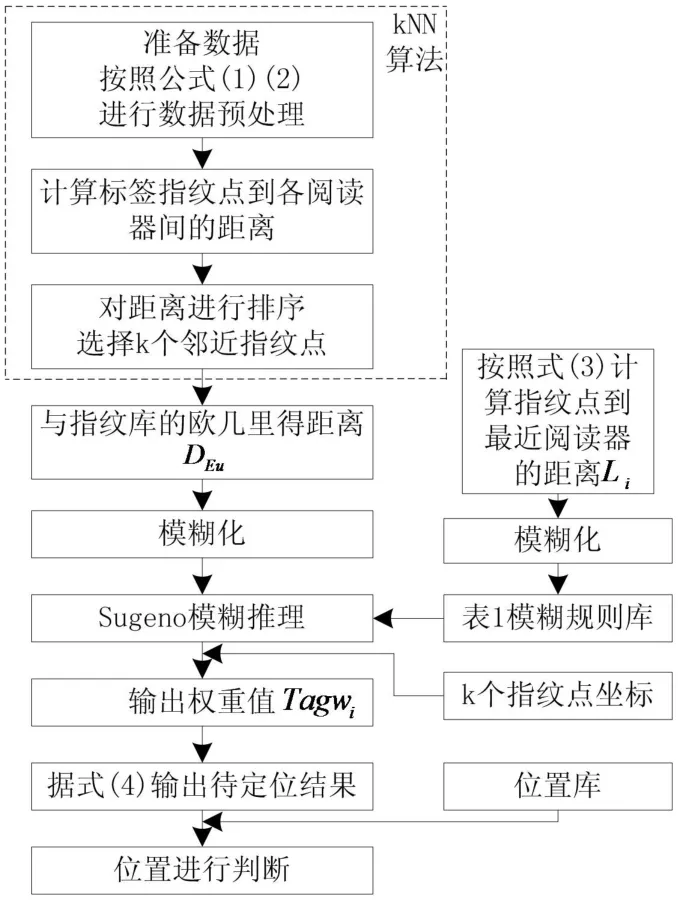
图4 算法流程图Fig.4 Algorithm Flow Chart
4 实验与仿真
实验时,在一套两居室套房内进行.如图5所示,实验环境置于该两居室的客厅,其房间大小为5.12m×5.21m,老人可在其房间内自由移动而进行测试信号的接收与定位.实验环境中,老人携带8个UHF标签,在安装有阅读器的客厅进行移动,如图6所示.
实验前,在无干扰环境中,对每个Tag进行接收的信号强度(Received Signal Strength Indication,RSSI)测试.实验中,阅读器从0m到5m对8个Tag进行RSSI误差测试,得到如表1所示数据,其中RSSI数据单位为分贝毫瓦(DeciBel relative to one Milliwatt,dBm).表2数据表明,标签Tag之间存在一定的信号误差,但此误差对定位精度而言,不会产生显著影响,无需特殊校准.
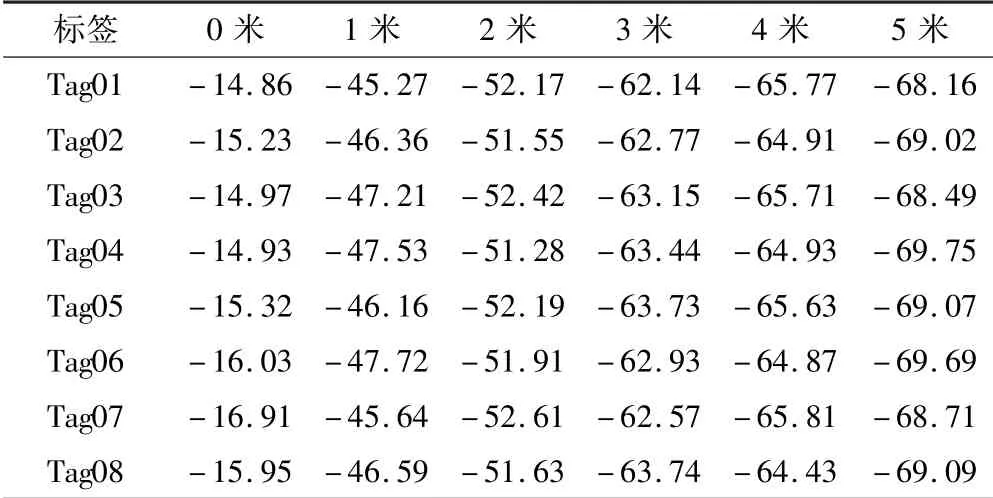
表2 标签信号误差测试数据表Table 2 Label Signal Error Test Data Table
实验环境示意图如图5所示,为一套2居室的套房,将阅读器按照如图6进行布置,测试老人客厅中行走,采集各阅读器测得的距离数据,通过算法计算得到老人具体位置.

图5 实验环境示意图Fig.5 Schematic Diagram of Experimental Environment
测试理想环境和真实环境下RFID信号随时间变化特性,得到如图6所示曲线.从图6可知,理想环境中,RFID信号随距离增加而减少,而真实环境中,在0m处测得数据与理想环境一致;而其他距离时,信号会受到真实环境中的各种物品的干扰而导致信号不随距离增加而减少.通过对RFID信号测试,得到阅读器安装位置和安装高度,如图7所示,阅读器安装高度为1.8m.
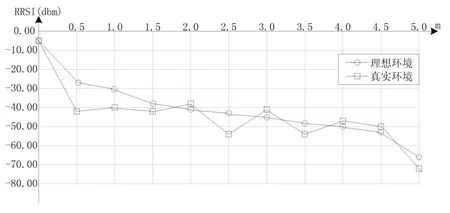
图6 RFID理想环境与真实环境测试曲线Fig.6 RFID Ideal Environment and Real Environment Test Curve
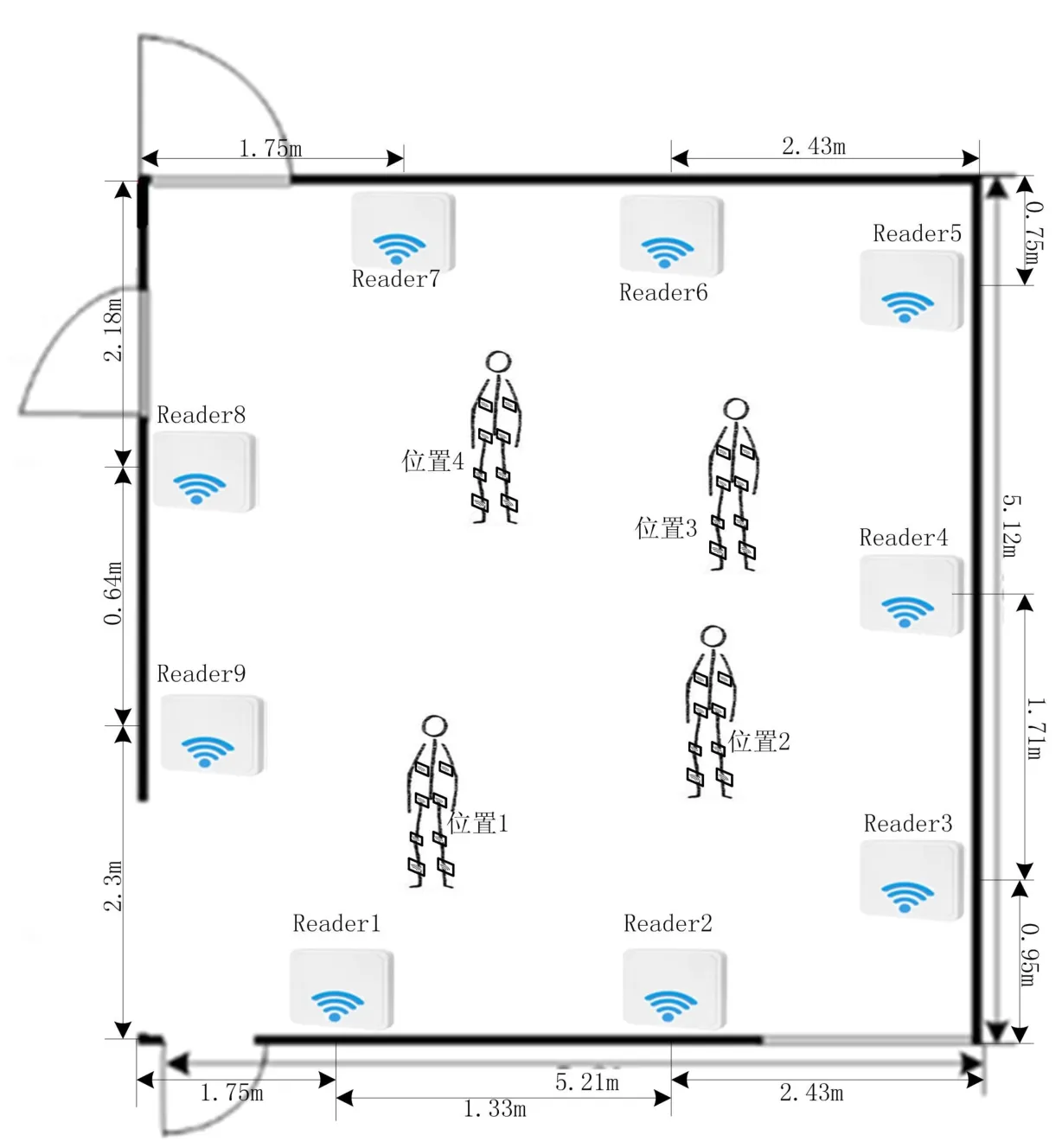
图7 阅读器位置示意图Fig.7 Schematic Diagram of Reader Position
将不同k值代入公式(1)和(2),并按照图4算法流程,测试不同k值时,系统定位精度,得到如图8所示曲线.由图8可知,当k值较小时,由于标签离阅读器的距离差异,导致定位误差比较大,如当k为2时,系统定位误差在55 cm附近,而随着k值增加,导致系统定位误差降低,k为8时,系统定位误差最小,到达几个厘米的精度.当k值由8开始增加时,系统定位误差呈现增长.由此,进行比较实验时,可选择k值为8.
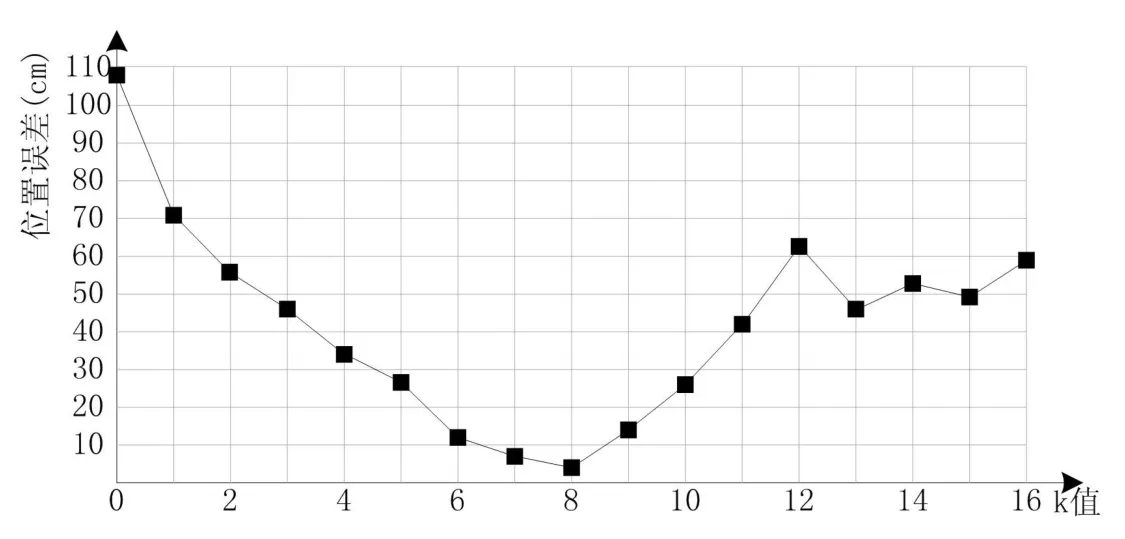
图8 不同k值定位误差曲线Fig.8 Positioning Error Curve of Different K Values
依据图8的不同k值定位误差,拟定k=8进行对比分析实验,参比为最邻近(Nearest Neighbor,NN)算法、KNN算法、贝叶斯算法和本文算法.定位误差为:
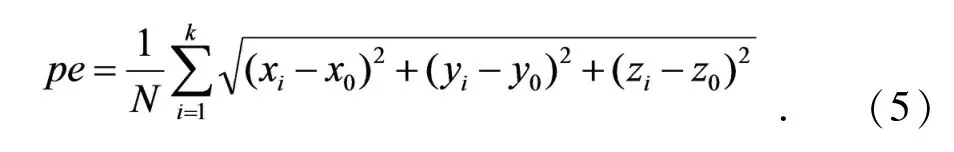
其中:(xi,yi,zi)为测试点坐标,(x0,y0,z0)为初始位置坐标,N为测试点数.
对比实验取N=40,进行四种算法定位实验,得到四种算法的定位误差比较曲线如图9所示.NN算法是最为基础的分类算法,需要进行一对一的匹配,故其定位精度较低.KNN算法是最常用而且有效的方法,但对各个节点数据利用不到位,需要进行各个节点数据加权处理.贝叶斯算法是利用概率统计进行分类的算法,方法简单、分类准确率高、速度快等优点.

图9 定位误差对比分析曲线Fig.9 Comparison andAnalysis Curve of Positioning Error
由图9可知,NN算法最小误差为20多厘米,这是由于NN算法需要一对一匹配,且随着数据测试点数增加,其定位误差较其他参比算法要大.KNN算法在测试点数据较少时,在定位误差比NN算法稍微低一点;当测试点数增加到6个及以上时,定位误差比NN算法总的趋势是降低.贝叶斯算法而言,较前两种算法,定位误差有所降低.本文算法,在测试数据为20个时,定位误差最小,仅为3厘米;而总的定位误差,较参比算法而言,在测试点数下,其值均有明显下降.
通过实验测试和仿真对比分析可知,本文算法在定位误差方面,有明显的改进.
5 结论
针对家居老人家居定位问题,提出一种模糊改进KNN的RFID定位算法.该算法利用阅读器读取老人携带的标签间的距离建立的距离信息指纹库,在KNN定位算法基础上,结合模糊推理方法,实现对家居老人的家居定位.首先设计了物联网RFID感知技术的家居老人定位模型,然后从RFID定位原理出发,设计了基于模糊推理的改进KNN的定位算法,并对所提出的算法进行了实验和仿真对比分析.通过实验和仿真对比分析,所提出的算法在定位误差方面,较参比算法优越.
