厚煤层综放开采顶煤分区破坏特征研究
2022-09-22韩宇峰王兆会唐岳松
韩宇峰,王兆会,唐岳松
(1.辽宁工程技术大学 矿业学院,辽宁 阜新 123000;2.中国矿业大学(北京) 能源与矿业学院,北京 100083)
0 引 言
放顶煤开采技术于20世纪80年代在平顶山煤矿工业试验成功,巨大的技术经济优势使其在我国得到迅速推广应用[1]。近年来,配套设备研制水平的进步极大提高了放顶煤开采的综合机械化程度。放顶煤工艺本身也得到重要改进,适用于大倾角煤层的大倾角放顶煤开采工艺,适用于特厚煤层(煤厚达14 m)的大采高综放开采工艺,适用于急倾斜特厚煤层的水平分段综放开采工艺相继出现[2],以满足不同赋存条件厚煤层开采的需要。综放开采技术在工艺和装备方面的突破性发展使其应用范围不断扩大,逐渐成为我国7 m以上厚煤层回采的首要技术选择。放顶煤开采技术存在3个核心理论问题:①顶煤破坏机理;②散体顶煤流动和放出规律;③大尺度采场围岩控制方法[3-4]。顶煤能够在架后均匀并及时冒落是放顶煤开采技术成功应用的前提,因此,顶煤能否破坏、冒落成为放顶煤开采设计遇到的首要问题。研究初期,矿山压力破煤作用得到重视,认为顶煤在支承压力作用下压坏,顶煤破坏特征同单轴抗压试验中煤样破坏形态相似[5];随着研究的深入,开挖卸荷引起的水平应力变化在顶煤破坏中所起的作用得到重视,顶煤由初始完整状态过渡至架后冒落状态经历了垂直应力加载、水平应力卸载和反向加载的复合作用,随着侧向约束的释放,顶煤逐渐被剪坏[5-7];文献[8-9]从损伤力学角度定义了顶煤损伤因子,认为顶煤强度符合Weibull分布,得到损伤因子同顶煤变形程度之间的关系,分析了顶煤损伤过程。顶煤破坏冒落后,在支架后方成为散体,散体顶煤流动和放出规律的确定是实现顶煤采出率最大化的保证。对于顶煤流动规律的研究最初借鉴金属放矿中的椭球体理论,忽略放顶煤支架对散体顶煤的影响[10];为使研究结果更贴近放顶煤工程实际,提出了考虑支架影响的散体介质流理论,在该理论的基础上经过大量的物理、数值模拟和现场实测,建立了以顶煤放出体、煤矸分界面和顶煤放出率为研究对象的BBR研究体系,初步建成可指导放顶煤工艺优化的散体顶煤放出理论体系[2,11-14]。采场围岩稳定是综放工作面安全、高效、快速推进的前提和基础,放顶煤采场一次采出空间大,为控制顶板稳定提出了“低位悬臂梁-高位砌体梁”覆岩结构模型,成功解释了综放工作面时常出现的“大-小周期来压”现象[15];工程实践表明,由于放顶煤工作面开采强度的提高,来压期间工作面支架同顶板之间存在动力接触现象,为使放顶煤支架适应大尺度采场的覆岩破断和运动特征,提出了支架阻力确定的动载荷法[16]。
对于散体顶煤流动和放出规律、大尺度采场围岩控制的研究,已初步形成较为严谨的理论体系,并在工程实践中得到成功应用。由于顶煤边界条件的复杂性,针对顶煤破坏机理的研究,目前较为普遍的方法是根据支承压力分布或实测裂隙分布对顶煤进行宏观分区,并没有形成严谨的理论支撑对顶煤破坏程度的判断。采用弹塑性理论得到各阶段顶煤所处的应力状态,进而确定各阶段顶煤破坏分区特征,以期促进对顶煤破坏机理的认识。
1 煤壁前方顶煤破碎分区
厚度为H的煤层采用综放开采,割煤高度为h,取工作面前方范围L内的煤体,建立力学模型如图1所示。范围L大于煤体超前破坏范围,坐标原点O处煤体变形接近0,可将边界x=0视为固定位移边界;工程实践表明煤层同直接底之间的接触面不会破坏,边界y=0同样可视为固定位移边界;顶煤上表面y=H承受非线性支承压力作用,为应力边界条件,此处为便于得到理论解,将支承压力视为线性载荷q(x)=fx+q。工作面煤壁x=L处,割煤高度(0,h)范围内为揭露煤壁,可视为自由边界条件,顶煤厚度(h,H)范围内承受控顶区顶煤悬臂结构作用于其上的条形载荷p和剪力τ。为得到所建力学模型的位移场和应力场,采用Ritz法进行力学分析[17]。
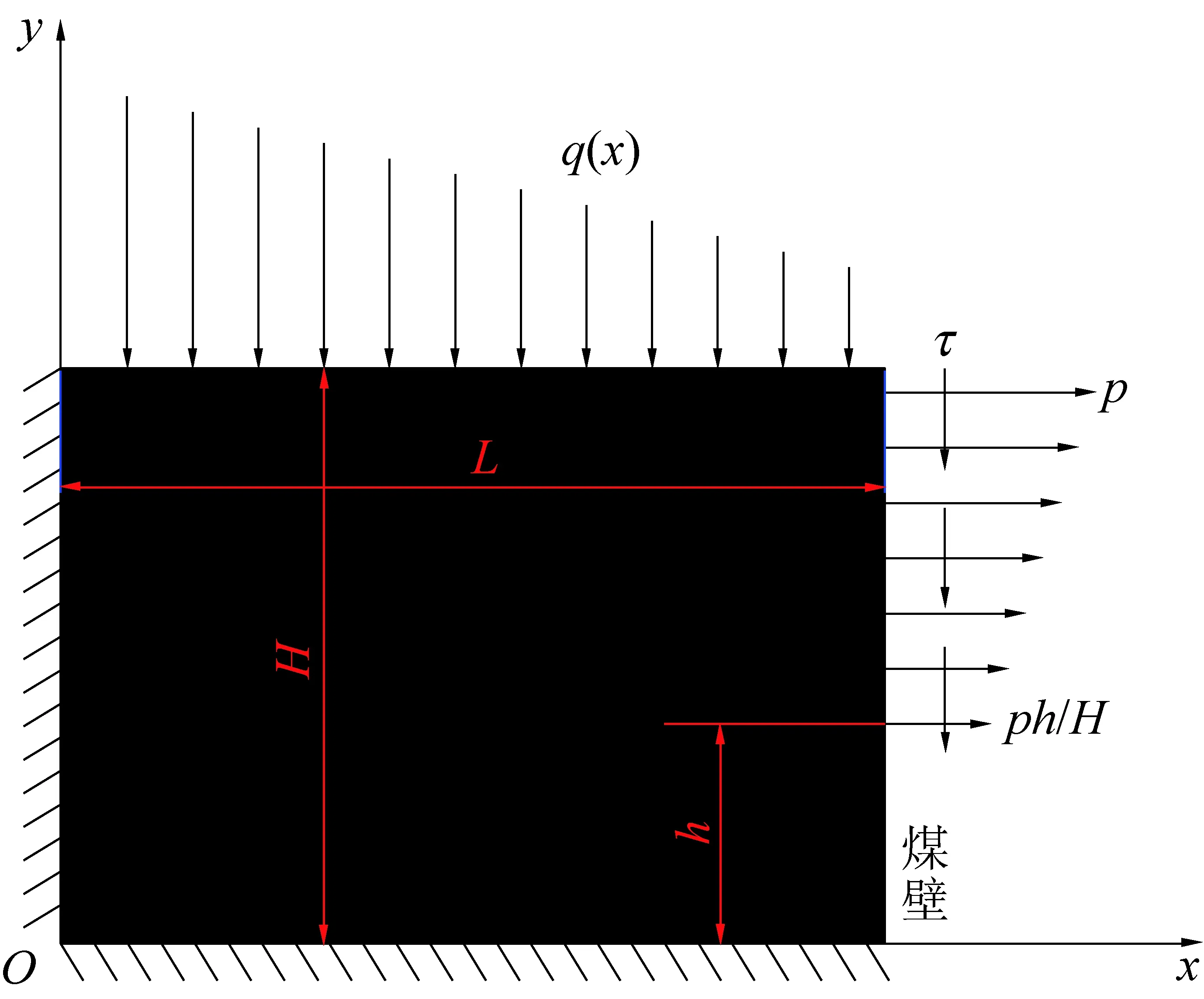
图1 煤壁前方力学模型Fig.1 Mechanical model for top-coal ahead of face line
根据力学模型的位移边界条件,在不计煤体自重的条件下,可设煤层各处位移分量为:
(1)
式中:ux和uy为水平和垂直位移,m;ai和bi为6个未知常数。
根据几何方程,顶煤沿各方向的应变分量为:

(2)
式中:Ma=a0+2a1x+a2y;Nb=b0+b1x+2b2y;Na=a0+a1x+2a2y;Mb=b0+2b1x+b2y;εx和εy为煤体在x和y方向上的应变分量;γxy为剪应变。
将式(2)代入本构方程可得煤体应力分量为:
(3)
式中:σx和σy为煤体在x和y方向上的应力分量;τxy为切应力。E为煤体弹性模量,GPa;ν为泊松比。
顶煤破坏问题可视为平面应变问题,力学模型沿z方向的厚度为1,因此,贮存于图1中的弹性应变能为:
(4)
将式(2)和式(3)代入式(4)可得贮存于煤体中的弹性应变能为:
(5)
根据建立力学模型的应力边界条件可得顶煤变形过程中,外载作用于其上的外力势能为:
(6)
图1力学模型的总势能为内力势能U同外力势能V之和:
II=U+V
(7)
结合式(5)和式(6)可知式(7)中存在ai和bi(i=0~2)6个未知常数。根据Ritz方法可知使力学模型总势能取最小值的那组位移为测试函数中的真实位移,借助位移变分原理,总势能取驻值的条件为:
(8)
由于δai和δbi任意且相互独立,则保证式(8)成立的条件为δai和δbi的系数分别等于0:
(9)
由式(9)可得关于ai和bi的6个非齐次六元一次方程组:
(10)

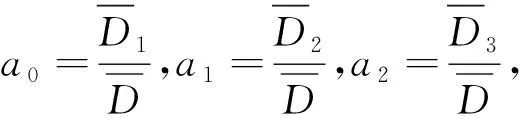
(11)

采用上述方法对山西新柳煤矿综放面顶煤分区破坏特征进行分析,目标工作面埋深260 m,煤层厚度8 m,普氏系数0.8~1.5,直接顶为页岩,随采随冒,基本顶为灰岩,致密且坚硬。工作面割煤高度3 m,顶煤厚度5 m,煤体走向范围L取12 m,煤体弹性模量取1.8 GPa,泊松比0.3,f取-0.5 MPa,q取10 MPa,p取2 MPa,τ取0.3 MPa。由以上参数可得工作面前方顶煤的位移场如图2所示:顶煤在水平方向产生拉伸变形,在垂直方向上产生压缩变形。最大拉伸变形出现在煤壁处顶煤上表面,达到8 cm;随着向工作面前方远离煤壁和顶煤层位的降低,水平变形逐渐减小。以力学模型的左上角和右下角连线为界,该直线左下方煤体水平变形值接近等于0,右上方变形值逐渐增大。顶煤竖向压缩变形明显大于水平拉伸变形,但其分布特征同水平变形相似,顶煤最大压缩变形达到14 cm,位于煤壁位置顶煤的上表面,随着远离煤壁和煤层层位的降低,压缩变形量减小。顶煤变形的理论分析结果与实测结果一致。
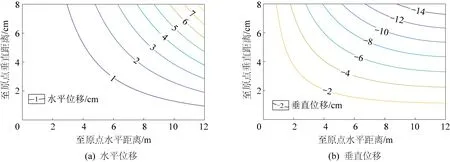
图2 顶煤位移等值线Fig.2 Contour line of top-coal displacement
工作面前方顶煤应力场如图3所示,受控顶区顶煤悬臂作用的影响,顶煤水平应力以拉应力为主,底煤受底板约束强烈,水平应力以压应力为主。同最大拉伸变形一致,最大拉应力出现在煤壁处顶煤上表面,最大值可达0.8 MPa。垂直应力呈线性分布,靠近煤壁位置处,接近施加的顶板载荷4 MPa,远离煤壁的工作面前方位置,垂直应力先缓慢升高,之后迅速降低,同初始施加的线性变化边界载荷出现较大偏差,这是由于建立力学模型的边界效应引起的。采用Ritz法分析问题时,受位移函数式(1)的影响,靠近力学模型位移边界的计算结果同实际情况会出现不同程度的偏差。在分析顶煤破坏问题时,研究的重点为煤壁附近的顶煤,远离煤壁的顶煤处于弹性状态,不是本文顶煤分区破坏讨论的重点,因此,Ritz法计算偏差可以接受,不会对分析结果产生影响。
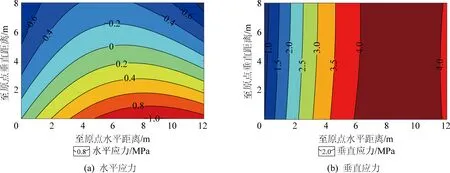
图3 顶煤应力场Fig.3 Stress distribution of top-coal
图1力学模型没有考虑初始地应力的影响,煤层采动不但造成垂直应力升高,开挖引起的卸荷效应还会造成水平应力降低。工作面前方水平地应力变化通常采用负指数函数进行描述[18]:
σh=α[exp(β(L-x))-1]
(12)
式中:σh为水平应力,MPa;α为地应力常数,MPa;β为反映采动影响强度的无量纲常数。
根据新柳煤矿地质条件,此处α取值2 MPa,β取0.08。采用应力叠加原理,将式(12)确定的应力值同图3a中的计算结果相加,可得到考虑初始地应力和开挖卸荷效应双重影响的水平采动应力。其分布特征如图4所示:应力叠加后,水平应力仍存在拉应力,最大值仍为1 MPa,位于煤壁处顶煤上表面位置,但同图3a相比,图4中的水平拉应力分布范围缩小。考虑初始地应力和开挖卸荷效应影响后的水平采动应力分布能够更真实反映顶煤的应力环境的变化过程。

图4 顶煤水平应力分布Fig.4 Horizontal stress of top-coal
为定量表征顶煤破坏危险程度,文献[19-20]定义了顶煤破坏危险性系数k为顶煤中任意一点应力状态确定的莫尔应力圆半径同应力圆圆心至强度曲线垂直距离之差:
(13)
式中:σ1、σ3分别为最大和最小主应力,MPa;C为煤体黏聚力,MPa;φ为煤体内摩擦角,(°)。
当k小于0时,顶煤处于弹性状态,k等于0,顶煤处于极限平衡状态,k大于0,顶煤进入破坏状态。将顶煤垂直应力和水平应力分别视为最大和最小主应力,煤体的黏聚力和内摩擦角分别取1 MPa和28°,由图3b、图4和式(13)可得顶煤破坏危险性系数分布如图5所示。k=0的等值线在工作面前方8 m处与顶煤上表面相交,在距离底板高度4 m处与下位顶煤相交。由该等值线开始,远离煤壁的方向,顶煤破坏危险性系数降低,成为负值,处于弹性状态;靠近煤壁的方向,顶煤破坏危险性系数升高,成为正值,进入破坏状态。纵向层位升高,顶煤超前煤壁的破坏范围增大。顶煤裂隙发育程度的实测结果表明,上位顶煤裂隙发育超前于下位顶煤[6],与理论分析结果一致。

图5 顶煤破坏危险性系数分布Fig.5 Distribution of coefficient k
对比图4水平应力等于0的等值线及图5破坏危险性系数等于0的等值线可知,水平应力等于0的等值线附近,顶煤处于单轴抗压状态,应力状态决定的应力圆为图6中的蓝色半圆。作用于破坏面上的正应力为应力圆同强度曲线切点A1的横坐标σ,为压应力,顶煤发生压剪破坏。顶煤继续向煤壁靠近,水平应力转变为拉应力,该区域顶煤应力状态决定的应力圆为图6中的绿色半圆,此时最小主应力虽然成为拉应力,但破坏面上的正应力仍为压应力,顶煤仍然发生压剪破坏。随着最小主应力的增大,当顶煤应力状态确定的应力圆为图6中红色半圆时,顶破坏面上的正应力减小至0并开始过渡为拉应力,顶煤开始发生拉剪破坏。
根据图6中的几何关系,顶煤发生拉剪破坏的条件为水平应力达到:

图6 应力圆同强度曲线关系Fig.6 Relation between Mohr circle and strength line
(14)
式中:σts为顶煤超前工作面发生拉剪破坏时的水平应力极限值,MPa。
顶煤黏聚力为1 MPa,内摩擦角为28°的条件下,红色应力圆的最小主应力为0.5 MPa,即水平应力大于0.5 MPa时,顶煤发生拉剪破坏。综上,由图4水平应力等于0.5 MPa的等值线靠近煤壁,顶煤发生拉剪破坏;远离煤壁,顶煤发生压剪破坏。
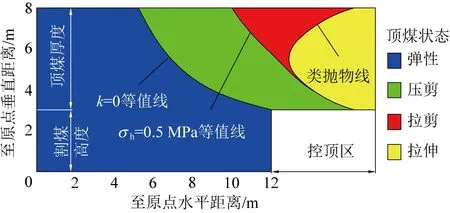
将图4水平应力等于0.5 MPa的等值线和图5破坏危险性系数等于0的等值线绘制成图7,破坏危险性系数等于0的等值线左侧蓝色阴影部分,顶煤处于弹性完整状态;右侧部分顶煤破坏危险性系数大于0,处于破坏状态。其中破坏危险性系数等于0的等值线同水平应力等于0.5 MPa的等值线之间的绿色阴影部分,顶煤剪切破坏面上的正应力为压应力,发生压剪破坏;水平应力等于0.5 MPa的等值线至煤壁范围内的红色阴影部分,顶煤破坏面上的正应力为拉应力,发生拉剪破坏。
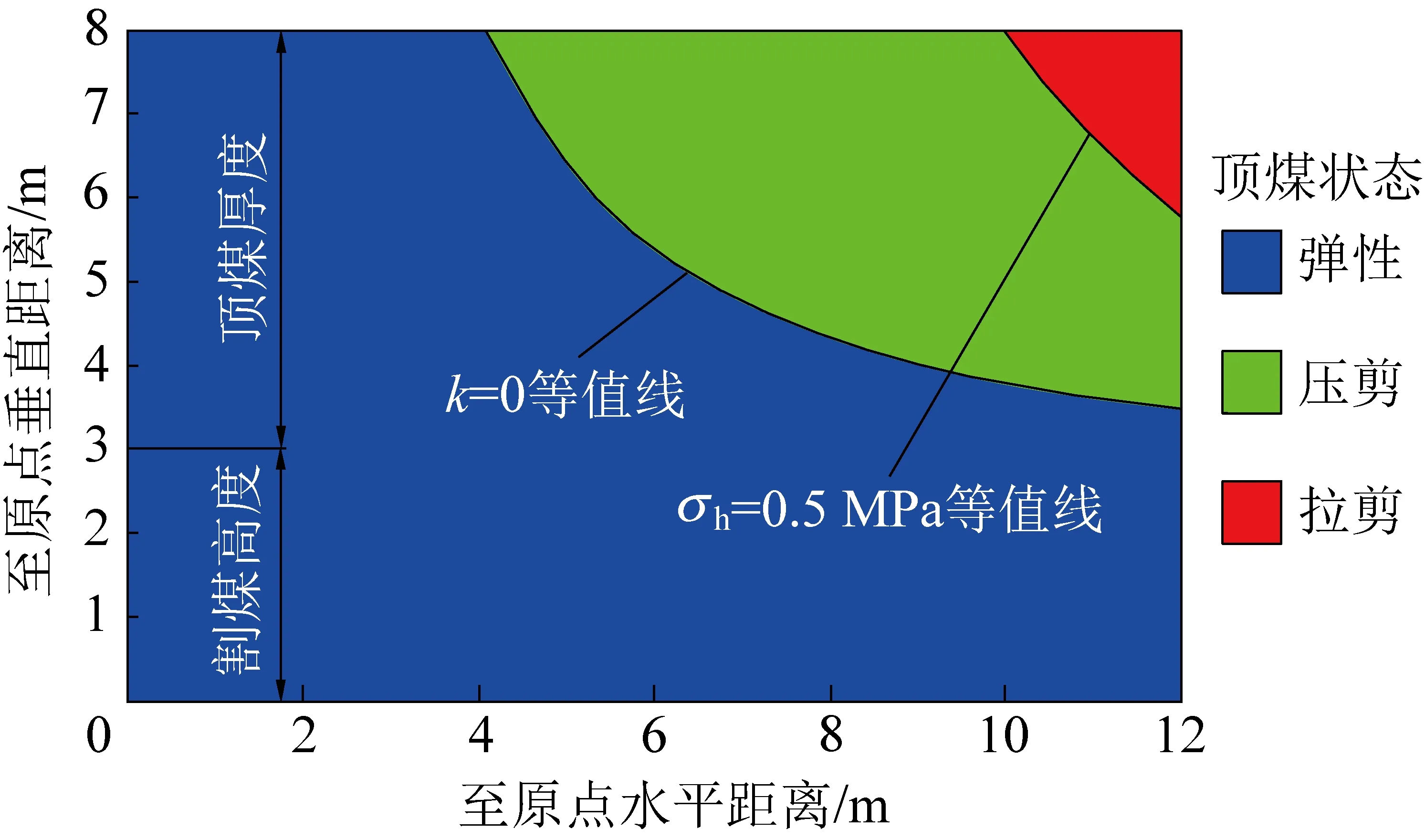
图7 煤壁前方顶煤破坏形式分区Fig.7 Failure zone of top-coal ahead of face line
2 煤壁后方顶煤破碎分区
控顶区顶煤可视为悬臂梁,支架简化为刚度为K的弹簧,建立控顶区受支架支撑的顶煤悬臂梁力学模型如图8所示。力学模型的总势能II包括顶煤弯曲应变能、支架弹性势能和顶板载荷做功而产生的外力势能,由式(15)确定:
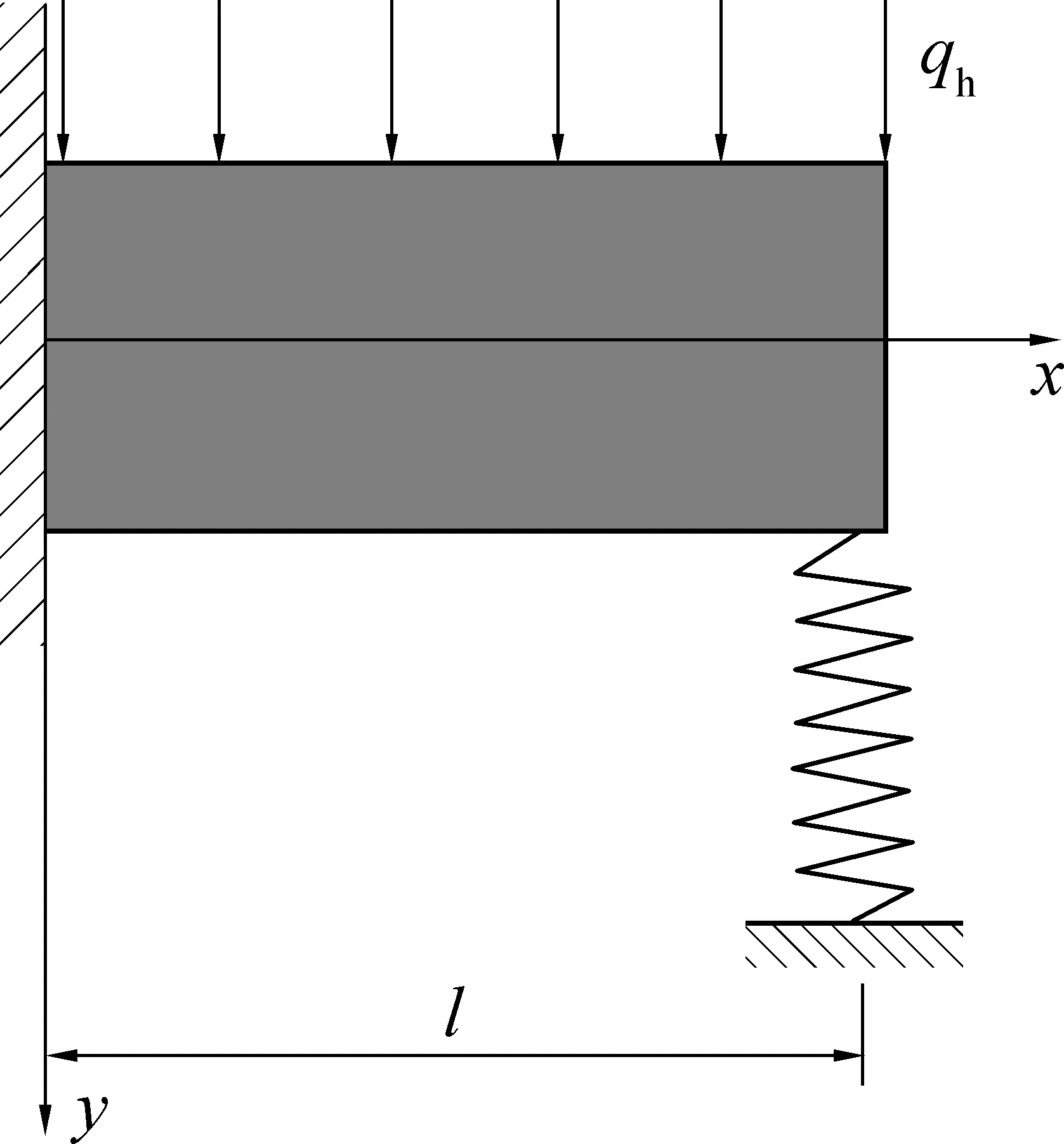
图8 顶煤悬臂梁模型Fig.8 Mechanical model of top-coal behind of face line
(15)
式中:E为弹性模量,GPa;I为惯性矩,m4;w为悬臂梁挠曲,m;l为控顶距,m;qh为顶板载荷。
根据最小势能原理,令顶煤总势能的一次变分等于0:
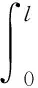
(16)
为求解微分方程,对式(16)第1项进行分部积分(上角括号为求导阶数)可得:
(17)
煤壁一侧视为固支端,该侧顶煤位移和转角均为0,将上述边界条件代入式(17)可得:
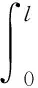
(18)
由于变分δw和δw′是任意的且相互独立的,由式(18)可得:
(19)
EIw(4)-qh=0(0 (20) 式(20)为顶煤弯曲变形的平衡微分方程,结合边界条件可得微分方程的解为: (21) 由式(21)可得控顶区域顶煤中水平应力分布: (22) 控顶区顶板载荷qh取1 MPa,顶煤弹模取0.2 GPa,控顶范围取5 m,则顶煤中水平应力分布如图9所示,上位顶煤水平应力为拉应力,最大值位于煤壁处顶煤上表面,随着距煤壁距离的增加,应力水平逐渐降低,距煤壁约为3.0 m处,水平拉应力消失。下位顶煤水平应力为压应力,距煤壁约为3.0 m处,自重作用导致下位顶煤中出现拉应力。 图9 控顶区顶煤水平应力Fig.9 Horizontal stress of top-coal behind face line 图9表明控顶区范围内,距煤壁较近的上位顶煤继续发生拉剪破坏,下位顶煤则在支架的反复支撑作用下发生压剪破坏。顶煤悬臂梁中拉剪塑性区发育形状为类抛物线形[21],如图10所示。抛物线右侧,顶煤在自重作用下发生拉伸破坏并冒落[3,22]。由图10可以看出,由初始完整状态过渡至架后冒落状态的过程中,以破坏危险性系数k=0等值线、水平应力σh=0.5 MPa等值线和控顶区上方抛物线形拉剪破坏边界线为界,顶煤先后经历了弹性压缩、压剪破坏、拉剪破坏和拉伸破坏4个阶段,最终在自重作用下于支架后方冒落。 图10 顶煤破坏形式分区Fig.10 Failure zone of top-coal 为验证理论分析结果的正确性,以山西新柳煤矿为工程背景,采用FLAC3D数值计算软件建立平面应变数值模型,模型长200 m,高120 m,两侧和底部为固定位移边界条件,顶部为应力边界条件,模拟覆岩自重。煤层厚度8 m,割煤高度3 m,顶煤厚度5 m,对综放开采过程进行数值模拟,定义FISH函数,当顶煤和顶板发生拉伸破坏时便开始冒落,覆岩冒落岩块足以充满采空区时对采空区进行回充,具体模型参数和模拟过程详见文献[3,22],此处不再赘述。煤层采动后,截取顶煤附近区域如图11所示,对其分区破坏特征进行分析。采用如下方法对煤体破坏形式进行区分:定义煤体状态参数λ,当煤体处于弹性状态时,λ=0;当煤体发生压剪破坏时,λ=1;当煤体发生拉剪破坏时,λ=2,当煤体发生拉剪-拉伸混合破坏时,λ=3;当煤体发生拉伸破坏时,λ=4。 图11 顶煤破坏数值模拟结果Fig.11 Numerical results of failure region 远离工作面的顶煤处于弹性状态,如图11中的蓝色区域。顶煤超前工作面约13 m开始发生压剪破坏,如图11中青色区域,此时顶煤没有完全进入塑性屈服状态,仅产生相互平行的剪切破坏带。上述剪切破坏带实质为塑性流动理论中的滑移线,滑移线在顶煤中成簇发育,而不是均匀发育,这是由于煤体变形破坏过程中具有变形局部区域集中化的特点。超前工作面距离继续减小,顶煤水平应力在开挖卸荷作用下快速释放,局部剪切破坏带逐渐扩展,工作面前方2 m处,顶煤全部进入压剪破坏状态。工作面前方1 m处顶煤进入拉剪破坏状态,如图11中的绿色区域所示,压剪破坏区域同拉剪破坏区域交界线上顶煤应力状态可由图6中的红色莫尔应力圆表示,拉剪破坏带一直延展至控顶区上方,呈漏斗状,同图10理论分析结果一致。在拉剪破坏带的左侧,顶煤并非直接进入理论分析中的拉伸破坏范围,而是存在一条宽度较小的剪切-拉伸混合破坏带,如图11中的黄色区域,剪切-拉伸混合破坏带呈不规则形态分布,由于宽度较小,顶煤经历该阶段的时间很短。顶煤于煤壁后方进入拉伸破坏范围,如图11中的红色区域,经历拉伸破坏过程之后,顶煤中的采动裂隙发育程度达到较高水平,顶煤抗拉强度减小甚至消失,在自重作用下于支架后方冒落。 液压支架侧护板之间沿工作面走向在顶煤中打倾斜钻孔,采用YTJ20型岩层探测记录仪对顶煤变形破坏过程进行观测,结果如图12所示,其中A、B和C三点为顶煤同直接顶之间接触面的变形破坏情况,点D和E为顶煤破坏情况。 图12 顶煤变形破坏特征Fig.12 Failure characteristics of top-coal 工作面前方10 m(A),顶煤同直接顶之间接触面保持完整,此时顶板弯曲变形程度低,接触面承受的法向压力及自身强度参数足以使其抵抗和传递顶板作用于顶煤之上的水平剪力,接触面保持完整状态;煤壁上方B点,顶煤同直接顶之间的接触面出现离层,破坏接触面下位顶煤中发育有微小的纵向裂隙;在控顶区域上方(C),顶煤下表面转变为受支架支撑的应力边界条件,工作面推进过程中支架立柱反复升降导致控顶区顶煤下表面周期性失去支架支撑,成为自由边界条件,控顶区顶煤自由弯曲下沉,最终导致顶煤同直接顶之间的接触面完全破坏,并发生明显的位错滑移。此次钻孔采用的钻头直径为36 mm,对比滑移量同钻孔直径可以确定顶煤同直接顶之间的最大滑移量,其数值为10 mm。工作面前方8 m(D),顶煤中没有出现较大的宏观裂隙,钻孔仅出现较小的收缩变形,孔壁出现少量的闭合型裂隙。表明该位置顶煤在顶板的束缚作用下,水平应力不能有效释放,顶煤发生剪切破坏;在控顶范围内的E点,顶煤中出现大量张开型拉伸裂隙,且存在塌孔现象,顶煤被切割成块度较小的煤块。表明顶煤同直接顶之间的接触面完全破坏,对顶煤的束缚效应降低甚至消失,水平地应力被完全释放,且顶煤经历了多次支架反复升降立柱过程,在悬臂作用下顶煤中出现一定水平的拉应力,顶煤发生拉伸破坏。 1)工作面前方顶煤水平位移、垂直位移、水平应力、垂直应力均在煤壁处顶煤上表面达到最大值,采用应力叠加手段得到同时考虑初始水平应力大小和开挖卸荷效应的采动水平应力分布形式;控顶区上位顶煤承受水平拉应力,下位顶煤则承受水平压应力。 2)将顶煤剪切破坏划分为压剪和拉剪2种形式,推导出2种破坏形式的过渡条件;借助莫尔-库伦强度准则定义顶煤破坏危险性系数k,以k=0等值线、水平应力σh=σts等值线和控顶区上方抛物线形拉剪破坏边界线将顶煤划分为弹性状态→压剪破坏→拉剪破坏→拉伸破坏4个变形阶段。 3)数值结果表明顶煤存在弹性状态→压剪破坏→拉剪破坏→剪切-拉伸混合破坏→拉伸破坏5个阶段,梯形压剪破坏区和漏斗形拉剪破坏区同理论分析结果一致;实测结果表明工作面前方顶煤出现闭合型剪切裂隙,后方出现张开型拉伸裂隙,与理论分析所得顶煤分区破坏特征一致。
3 顶煤破碎分区数值验证

4 顶煤裂隙发育特征实测
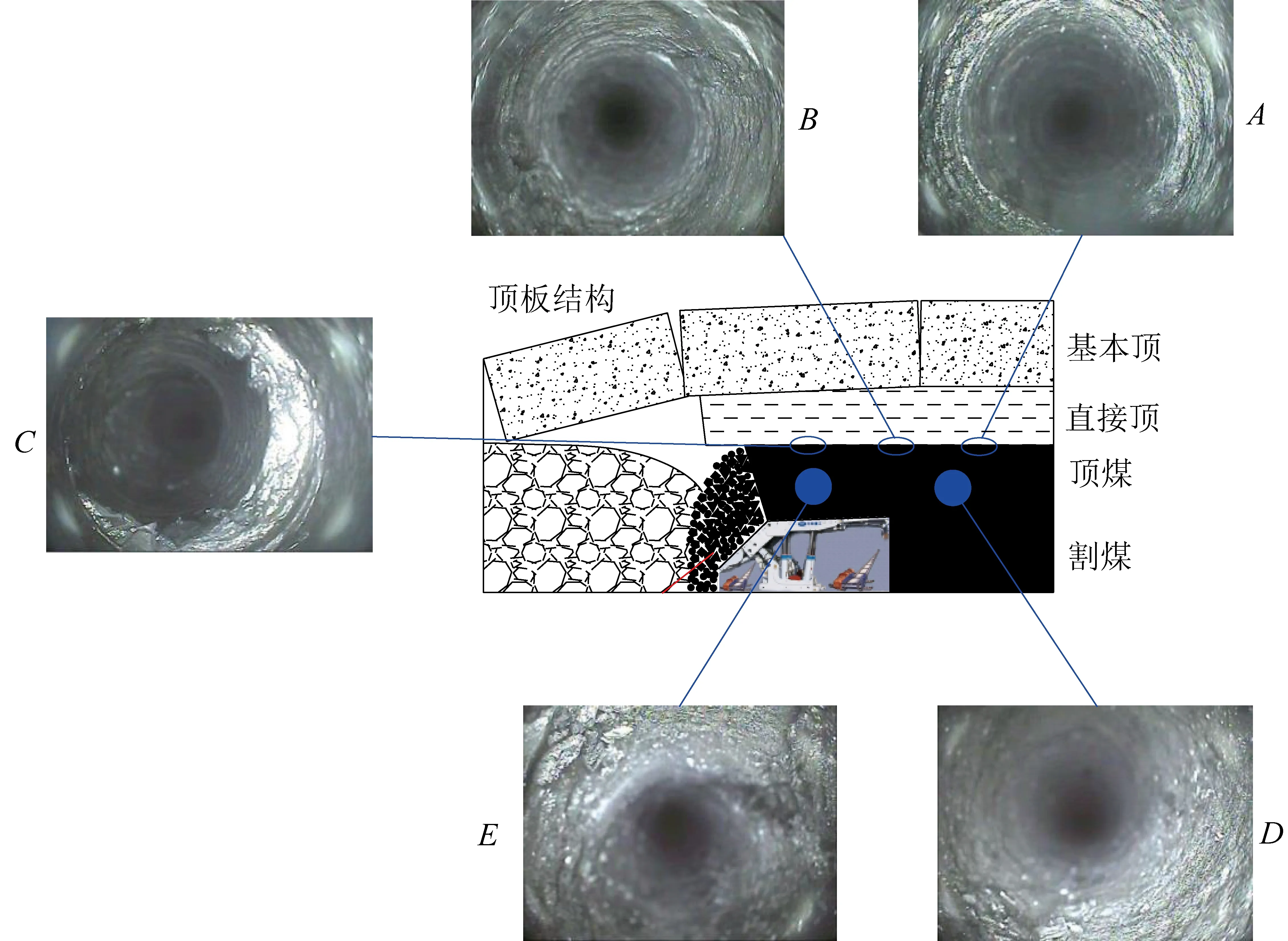
5 结 论
