基于DEPSO算法的城镇燃气管网阻力辨识

1 概述

《国民经济和社会发展第十四个五年规划纲要和2035年远景目标》明确提出“要探索建设数字孪生城市”。作为城市能源系统中不可或缺的一部分，针对城镇燃气管网系统的数字孪生技术研究也方兴未艾。其中，管网系统的模型辨识作为物理系统映射至信息系统的基础，是数字孪生系统中最重要的部分之一。一方面，管道内壁随运行时间增加会发生腐蚀、磨损，但是其对管道摩擦阻力系数的影响难以估计；另一方面，燃气管网中弯头、三通等的局部阻力难以精确计算。由此带来的相对误差必须通过阻力辨识的手段予以消减，才能为管网的智能调控以及泄漏检测提供技术上的支持。因此，作为管网数字孪生系统中的关键一环，管网系统的阻力辨识问题一直以来都是学界关注的焦点。

随着管网规模不断增大，传统的数值算法在阻力辨识问题上逐渐失效，与此同时智能优化算法不断兴起，因此更多学者开始采用智能优化算法作为求解的手段。其中，被采用最多的就是遗传算法(Genetic Algorithm，简称GA)和以遗传算法为主体的混合算法

。时至今日，差分进化算法(Differential Evolution，简称DE)作为新兴的智能算法之一，其在高维问题上相较遗传算法展现出更好的收敛性以及鲁棒性，不断受到相关领域的重视

。已有学者将DE应用在供水管网阻力辨识问题中，取得了较GA更好的结果

。另外，在优化算法领域部分学者以DE以及与粒子群算法(PSO，Particle Swarm Optimization，简称PSO)为母体形成的混合算法(简称DEPSO)，在一系列高维的测试函数上都表现出了较DE、PSO算法更好的性能

。

本文提出一种基于DEPSO的城镇燃气管网阻力辨识方法，并通过虚拟管网以及实际管网对该方法进行验证。

2 阻力辨识数学模型

2.1 管网仿真模型

本文采用等温稳态方法对燃气管网工况进行模拟。常用的水力计算方法有解环方程法、解节点法以及解管段法，绝大多数燃气管网水力计算采用解节点法

。通过验证采用Newton-Raphson方法计算精度较高

。仿真计算以式(1)为压力降计算公式，另外加入各节点流量平衡方程，形成管网方程组。本文涉及的压力均为绝对压力。标准状态指压力为101 325 Pa，温度为273.15 K。本文的管径均指管道内直径。

(1)

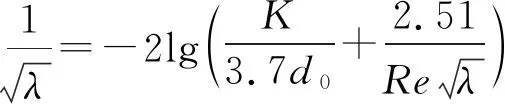
(2)

式中

、

——管道起点、终点压力，Pa

——管道摩擦阻力系数

——标准状态下燃气体积流量，m

/s

防治方法：冬前翻耕土地，浇水淹地，减少越冬虫源。根据虫情测报，在棉铃虫产卵盛期，结合整枝，摘除虫卵烧毁；生物防治成虫产卵高峰后3～4天，喷洒Bt乳剂、HD-l苏芸金杆菌或核型多角体病毒，使幼虫感病而死亡，连续喷2次，防效最佳；物理防治用黑光灯、杨柳枝诱杀成虫。当百株卵量达20～30粒时即应开始用药，如百株幼虫超过5头，应继续用药。一般在辣椒或茄子果实开始膨大时开始用药，每周1次，连续防治3～4次。

——管径，m

——标准状态燃气密度，kg/m

——标准状态压力，Pa

天花粉化学成分的药理活性及其提取与检测方法研究进展…………………………………………………… 丁建营等（13）：1859

——燃气温度，K

——标准状态温度，K

——燃气实际状态下的压缩因子

——燃气标准状态下的压缩因子

——管道长度，m

周淑英的作品让人们更多了解了中国民间艺术的风采，向世界展示中华民族的智慧、勤劳和尚美。她的作品《彩福图》被日本前首相鸠山由纪夫收藏；她多次赴法国、比利时等欧洲国家进行剪纸表演、展览，并受到总统、首相的接见；她的作品被多个国家部委指定为对外交流的互赠礼品；她几乎拿遍了国内外工艺美术界的大奖……胡锦涛同志在看过周淑英作品后感慨：“只有中国妇女才能创作出如此优秀之作！”

——工况数量

——雷诺数

2.2 辨识参数选择

不同管网系统由于仿真方式存在差异，面对阻力辨识问题所选用的辨识参数也不同。供水管网大多采用海森威廉公式进行水力计算，因此辨识参数一般为海森威廉系数，如郭伟

、Kang等人

的研究。供热管网一般选用管道阻抗作为辨识参数，如周志刚等人

、刘永鑫等人

的研究。相对供热管网，燃气管网中压部分可能存在部分过渡流甚至层流，因此不适合以阻抗作为辨识参数。因此结合式(1)可以确定较为合适的参数应为管道内壁当量绝对粗糙度或者管径。但是，一方面相较管径，管道内壁当量绝对粗糙度更加难以获取；另一方面管道内壁当量绝对粗糙度变化对管道压力降的影响相较管径更不明显，如果试图将管网中其他因素对阻力的影响(如三通、弯头等局部阻力件及管道中轻微堵塞等)叠加进管道内壁当量绝对粗糙度，界定其取值范围也更为困难。因此，本文采用管径作为辨识参数，并经过计算研究将管径参数界定在参考管径

的0.8～1.2倍。

2.3 辨识问题数学模型

式中

——阻力辨识目标函数

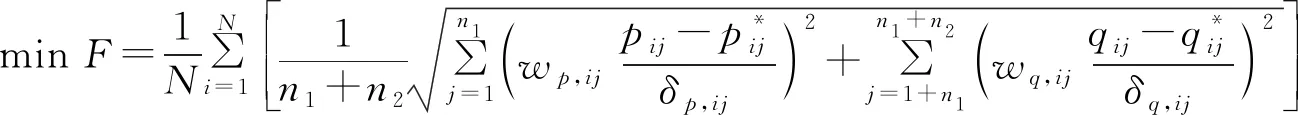
利用siRNA构建干扰模型，转染效率如图1A、B所示，转染效率达95%以上;干扰效率验证如图1C所示，与NC组相比，SI组LncRNA SNHG16表达水平明显降低(P＜0.01)，干扰效率达到(70.3±6.5)%;C组与NC组LncRNA SNHG16相对表达水平比较差异无统计学意义(P＞0.05)，可进行后续研究。

(3)

0.8

≤

≤1.2

管网中部分测点数据需作为管网仿真的计算条件，具体为气源点和用户节点数量之和的测点数，此时水力方程组恰好正定可解。除此之外的压力及流量测点将被纳入辨识问题的目标函数之中。在考虑到各测点精度差异的情况下，以管网中仿真结果与各测点数据差距最小为目标，建立优化目标函数如式(3)所示。式(3)中压力测点权重取1，流量测点权重为流量占管网总流入流量的比例。

文章讨论了大豆根系虚拟模型的构建方法，设计了大豆根系的L系统，并在VC++环境下采用OpenGL技术实现了其可视化，分析了各参数对根系模型的影响，生成的大豆根系图像具有随机性，在形态结构上与真实根系图像比较接近。但是，试验数据是在没有考虑水分、光照等环境因素下获取的，加之根系数据采集手段的局限性等因素，与自然环境下的数据之间还存在一定的差异，在后续的研究工作中，应进一步结合大豆根系的生理特征进行模拟，为大豆根系模拟研究提供技术支持。

——管道内壁当量绝对粗糙度，m

——工况编号，

=1，2，…，

、

——纳入目标函数的压力测点数量、流量测点数量

——测点编号，

=1，2，…，

+

,

——

工况下，

压力测点权重

——

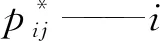
工况下，

压力测点测量值，Pa

基于PCA降维建模方法的主要思想是首先用PCA对废水数据进行特征提取，将选取好的主成分所对应的得分向量作为SVR和ANN模型的输入端，从而建立模型。该模型既具有PCA的数据压缩和降维功能，简化了工作量，又具有SVR和ANN的非线性建模能力[14]。基于PCA降维模型的算法流程图如图1所示。该流程图包括了原始数据的获取、数据预处理、主成分分析降维、SVR建模和ANN建模。

,

——

工况下，

压力测点的极限误差，Pa

,

——

工况下，

流量测点权重

调查显示，土壤侵蚀成因类型主要为水力侵蚀，陡崖与深切割沟谷伴有重力侵蚀和混合侵蚀。侵蚀形式整体以面蚀为主，也有沟蚀。面蚀伴随农耕、造林、垦荒、建筑材料开采及修筑公路等人为活动和生产过程出现，特点是侵蚀总量大，显见度低，潜在危害大。土层较厚的坡耕地，细沟侵蚀是面蚀的主要形态。沟蚀有集中性、偶发性、显见度高的特点。崩塌和泥石流常伴随暴雨、洪水发生。

——

工况下，

流量测点测量值，m

/s

2008年，北京奥运会开幕式上“和”字积木的变形表演再一次向世界与国民重申了中国当代的治国方针，并试图唤醒国民意识中的民族教义，抚慰国民历经百年断裂也难以抛弃的中华民族情结。似乎在“和”字的共振中，中国当代社会建设终于可以在话语权中稍显理直气壮地不再人云亦云、亦步亦趋，而在中华传统文化中找到立身之根本。所有反对崇洋媚外，忧虑西学殖民，要为中国传统文化寻一条出路的仁人学子，终于可以在“和谐”美学中找到底气。

,

——

工况下，

流量测点的极限误差，m

/s

——管网中各管段参考管径，m

——管网中各管段管径，m

2.4 数学模型的目标函数分析

在优化问题中，表征出目标函数

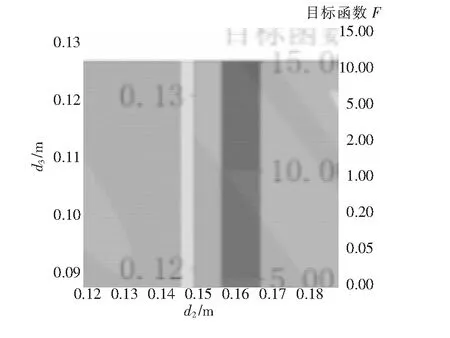
在可行域内的取值将对后续智能优化算法的设计提供帮助。为降低问题维度，分析采用的简单环网见图1，并设定管道内壁当量绝对粗糙度为0.1 mm。本文共采用3组不同工况作为研究对象，具体工况参数为：节点1为气源点，定压为3.5 MPa；节点3为用户节点，各工况流量分别为2.0、2.6、3.2 m

/s。纳入目标函数的变量为：节点1的流量、节点2与节点3的压力。在此设置条件下，对目标函数在0.8

ref，

≤

≤1

2

ref，

的取值情况进行表征，

为管段编号。

科研主管部门和高校每年都会投入大量的科研经费，但这些科研经费大部分是针对科研项目研究的，而在科研项目成果的教学转化，即科技成果教学转化上，支持力度基本没有或者较少。另外，科研项目在结题后，在一定的时间内结余的经费会由主管部门回收。而科技成果教学转化需要一定的物质和精力投入，也需要一定的资金支持。资金不足导致教师对科技成果教学转化的积极性不高、主动性不强，而在科研项目的经费中，并没有相应的科技成果教学转化项目，这使得即使科研项目经费有结余，教师也无法支出经费。

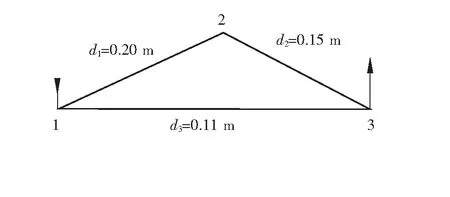
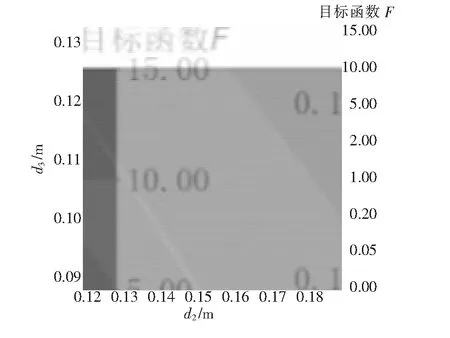
分别为0.18、0.20、0.21 m时，

、

分别在[0.8

,1

2

]、[0.8

,1.2

]内，目标函数

的变化情况见图2～4。

=0.20 m为设定值，其目标函数最小为0，为确定

=0.18 m及

=0.21 m时目标函数最小值，本文采用标准DE进行搜索，结果分别为1.81×10

以及3.07×10

。由图2～4及

=0.18 m、

=0.21 m时最小值状况，可以确定在全局最优解附近存在狭长的平坦区域。

3 阻力辨识求解算法

随着管网规模不断增加，需要辨识的参数维度更高，这将导致传统数值方法中梯度矩阵是高度病态的。因此阻力辨识问题需要采用智能优化算法进行求解。

3.1 智能优化算法

智能算法将每个可能的解视为一个个体，多个个体组成种群。算法模拟自然界动物的行为，不断对种群进行更新，从而得到优化问题的解。群智能算法包括GA、DE、PSO、蚁群算法、狼群算法等。

针对阻力辨识问题，本文将管网中的所有管径作为决策变量，将一组管径视为一个个体。在每次评价环节，每组管径与仿真计算所依据的测点数据相结合，进行仿真计算。计算将得到管网中所有节点压力以及节点流量，将计算结果与纳入目标函数的测点测量数据进行对比，即按照式(3)计算个体所对应的目标函数。

管网中管道数量动辄上千，这意味着问题属于大规模优化问题，需要算法在高维问题上有着较好的全局寻优能力。同时，由第2.4节分析可知，目标函数在全局最优附近存在狭长的平坦区域，需要算法后期有较好的局部搜索能力。因此本文以DE以及PSO这两种在高维问题上性能较好的算法为母体，采用双种群的形式，并以全局最优解作为交互信息，增强算法在最优解附近的搜索能力。

丰信农业创始人、总经理董金锋在接受《中国农资》记者采访时表示，未来，农业高质量发展离不开农服，农业挖潜离不开农服，农服一定会成为农业发展的一股洪流并将势不可挡。农服企业要联系实际，不断加强技术创新、组织创新、运营创新、服务创新，为现代农业发展助力。

.

.

差分进化算法

差分进化算法的种群更新基本步骤为：变异，交叉，选择。与其他进化算法最大的不同在于差分变异算子。变异算子随机选择两个个体相减生成差分变量，然后将差分变量赋予权重与任意随机产生的向量相加。DE/current to best/bin是一种较为常用的进化策略，能够较快收敛，具体变异方式见式(4)

。

=

+

(

1

-

2

)+

(

-

)

(4)

式中

、

——惯性权重的最小值、最大值

——父代个体

、

——放缩因子，介于[0,2]，一般取0.5

1

、

2

——父代随机个体，且

1≠

2≠

——当前代最优个体

本文采用二项式交叉(binomial)，见式(5)

。在选择前对种群每个个体进行适应度计算。采用一对一选择作为选择算子，即只有子代较父代有着更好的适应度时，才会被新种群接纳，否则父代个体将保留在下一代种群中。

(5)

式中

——子代个体

交叉后第

维度的值

——子代个体

交叉前第

维度的值

——父代个体

第

维度的值

——[1,

]的随机整数，

为决策变量维度

①仿真度高：优于真石漆，水包水喷涂出的建筑物仿大理石的效果逼真，纹理丰富，在视觉的界面内可以以假乱真并且水包水的表面平整不易积灰，能更久的保持外观效果，使用寿命长。

——交叉概率，一般设置为0.1，需快速收敛可设为0.9

.

.

粒子群算法

大学阶段是人一生中心理发展最为关键的时期之一，也是心理变化最激烈、最明显的时期。高校扩招和社会环境的变化给当代大学生带来了全新的挑战和各种各样的压力，有些大学生因难以应对这些挑战和压力而导致心理发展不平衡，情绪不稳定，心理矛盾与冲突。近些年来，大学生退学、堕落、自杀、自残、危害他人生命安全等事件时有发生，这些非同寻常的问题日益成为影响大学生健康成长的重要因素。探寻大学生精神疾病的根源，找到大学生思想压力的减压路径，是高校教育工作者面临的一项重要课题。

粒子群算法将种群中每一个个体视为没有体积的质点，在搜索空间中以一定初始速度飞行，并在飞行过程中不断根据个体经验以及群体经验动态调整飞行速度

。算法以全局历史最优位置作为速度更新的依据，形成各粒子速度与位置，分别见式(6)、(7)

：

(

+1)=

(

)+

[(

best，

(

)-

(

)]+

[

(

)-

(

)]

同时值得注意的是,在图9中,对应耦合间距d=170 nm的透射谱线中,出现了共振劈裂的现象,这是由于工艺缺陷等因素,微环侧壁出现了类似布拉格光栅的褶皱,使得微环腔中出现互耦合现象,微环腔理论上的最佳互耦合品质因数Qum与实际的互耦合品质因数Qu存在较大差异造成的[23],并不影响本文的研究结论。

(6)

(

+1)=

(

)+

(

+1)

(7)

式中

(

+1)——

+1代种群中个体

的速度

——当前代数

——惯性权重，一般设置为0.4～0.9

(

)——

代种群中个体

的速度

、

——学习因子，取值一般为0～4

、

——[0,1]内的随机数

best,

(

)——

代种群中个体

的历史最优位置

(

)——

代种群中个体

的位置

(

)——

代种群中搜索到的全局历史最优位置

(

+1)——

+1代种群中个体

的位置

在对种群更新后，需要计算种群中所有个体的目标函数，并确定适应度以确定当前全局最优位置。

另外，本文采用了如下的自适应策略

。

(8)

式中

——子代个体

——控制因子，通常取3

——最大迭代次数

3.2 DEPSO算法

本文以DE/current to best/bin以及PSO作为算法主体，算法分别作用在两个种群上，种群间以全局最优作为信息交互，增加算法在最优解附近搜索能力。DEPSO算法流程见图5，具体算法步骤如下。

① 初始化

初始化内容包括：DE种群规模

、PSO种群规模

，初始种群POP

、POP

(DE种群以及PSO种群简称为POP

以及POP

)，问题维度

，个体速度

；DE算法参数，

、

、

等；PSO算法参数，

、

等；最大迭代次数

。设置初始迭代次数

=0。

② 对种群进行更新

当

≤

时，对种群进行更新，更新策略如下：

a.获取并记录当前全局最优值为

，并与历史的全局最优值进行比较，判断

是否更新。

b.若

未更新，则转到步骤c，若

更新，则判断当前最优解存在于POP

还是POP

。若当前最优解存在于POP

，对当前最优个体赋予随机速度，将POP

中随机个体替换为当前最优个体；若当前最优解不存在于POP

中，即当前最优解存在于POP

中，将POP

中随机个体替换为当前最优个体。

c.对POP

：采用式(8)计算当前自适应的

并根据式(6)、(7)执行PSO操作，更新种群以及各个体历史最优解。对POP

：根据式(4)、(5)执行DE/current to best/bin操作。在各种群适应度计算环节，对POP

以及POP

中每个个体的目标函数进行计算，即采用每组管径以式(1)、(2)进行仿真计算并按式(3)计算目标函数，目标函数越小则个体适应度越高。

d.

=

+1，判断

≤

是否成立。若成立回到步骤a，否则输出计算结果。

4 结果探讨

4.1 仿真模型验证

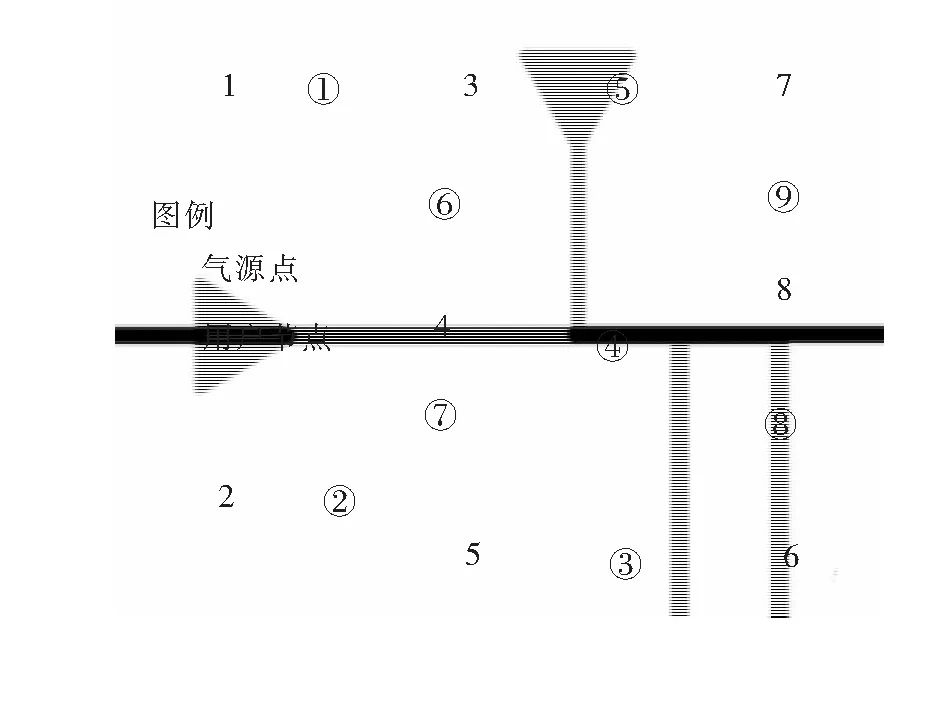
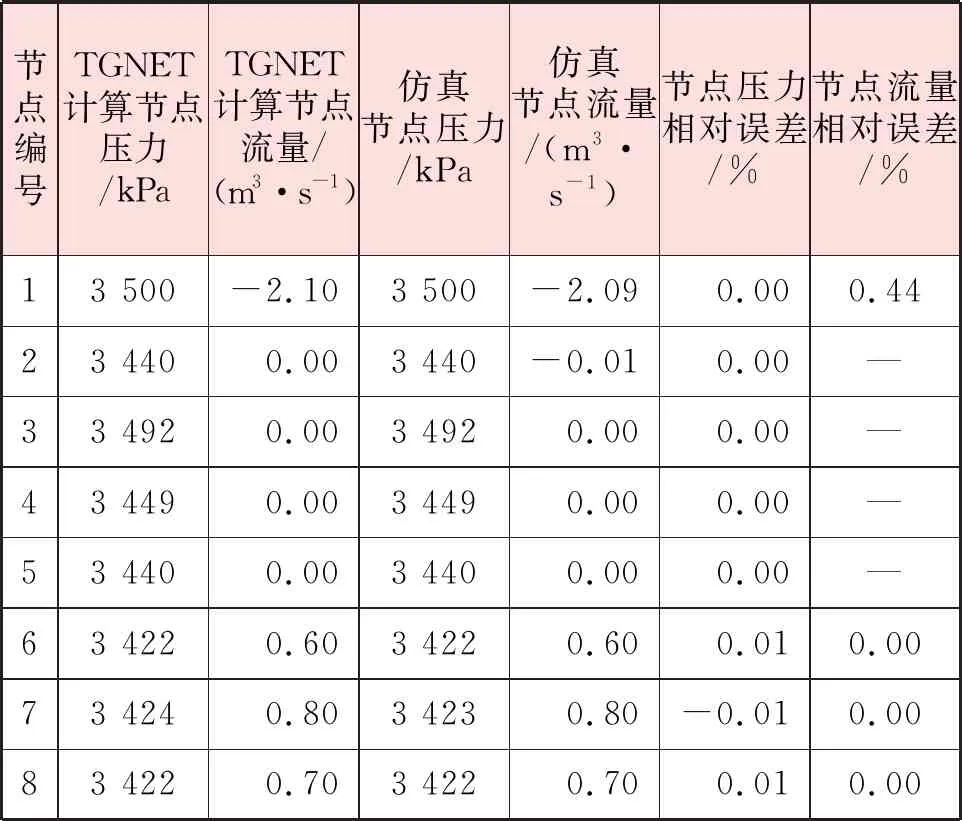
验证所用虚拟管网由上海叁零肆零科技有限公司提供的实际项目场景简化而来，仿真计算虚拟管网见图6，虚拟管网参数见表1。以节点1、2节点压力以及节点6、7、8节点流量作为仿真计算条件。将仿真结果与TGNET计算结果进行对比，见表2，显示仿真相对误差绝对值在1%以下，结果可信。

4.2 虚拟管网阻力辨识验证

采用图6所示的虚拟管网进行验证。根据管网中气源点1、2节点压力以及用户节点6、7、8节点流量经过TGNET计算，生成5组工况数据，各工况参数见表3。

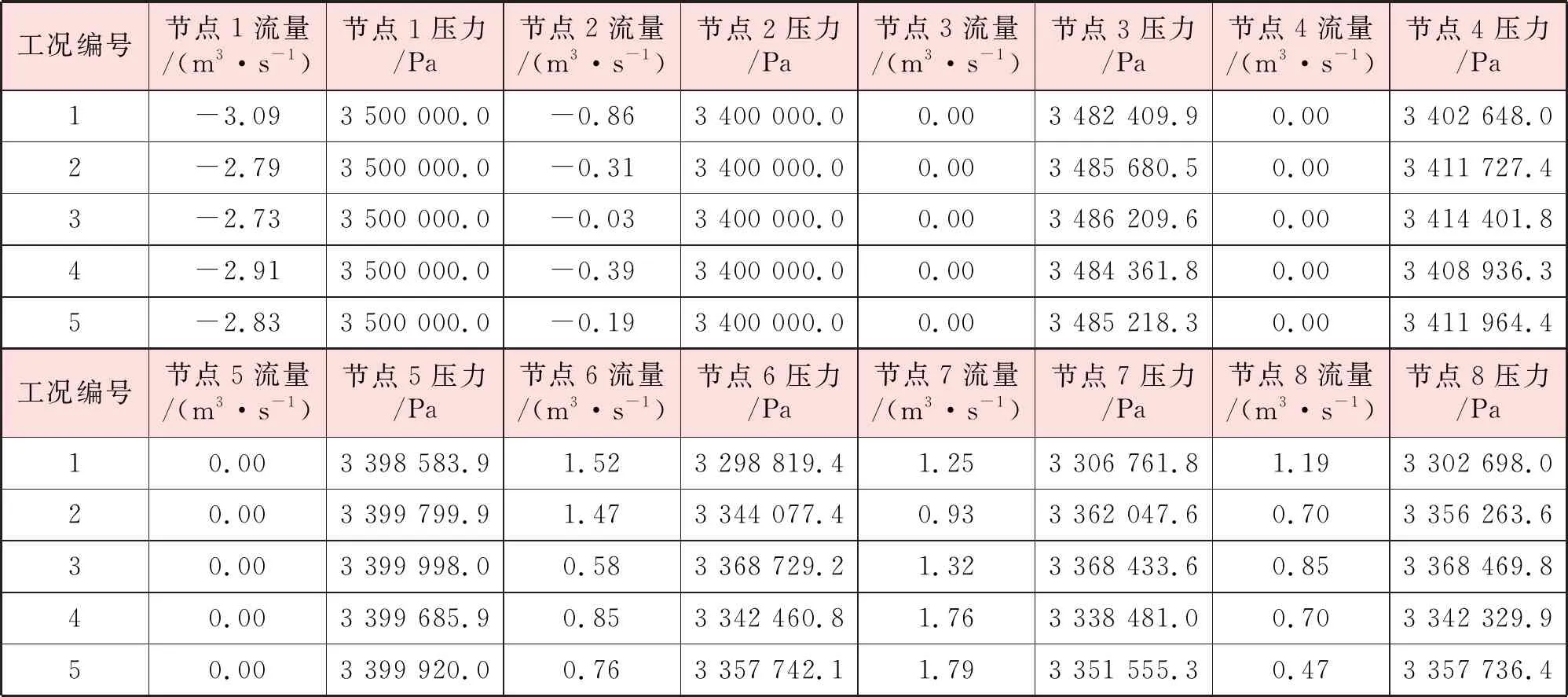
本文利用工况1～4进行辨识，并在工况5上进行仿真结果验证。辨识过程中适应度计算需经过仿真计算，仿真计算依据节点1、2的压力以及节点6、7、8的流量，除此之外，将节点1、2的节点流量以及节点4、6、7、8的节点压力视为测量数据，纳入目标函数计算中。

管网中压力测点精度设定为0.1%，流量测点精度为1%。辨识前采用设定管径进行计算，目标函数为0.094，这是仿真计算方法与TGNET之间存在误差所导致。

DEPSO算法各参数取值为：

=

=0

5，

=0.5，

=0.4，

=0.6，

=

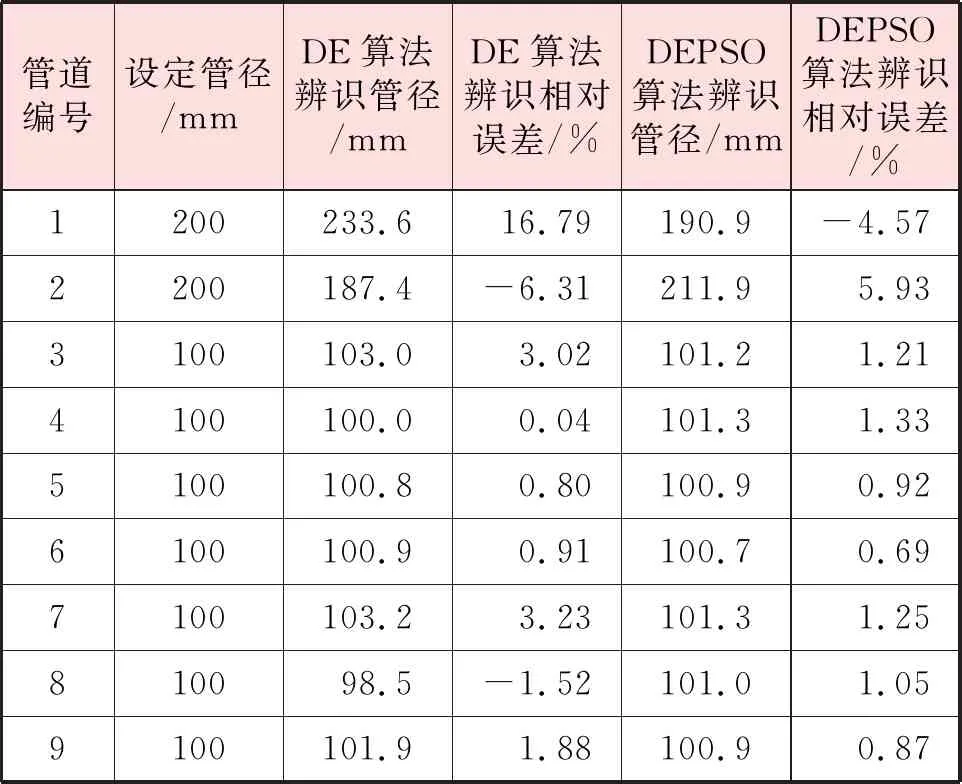
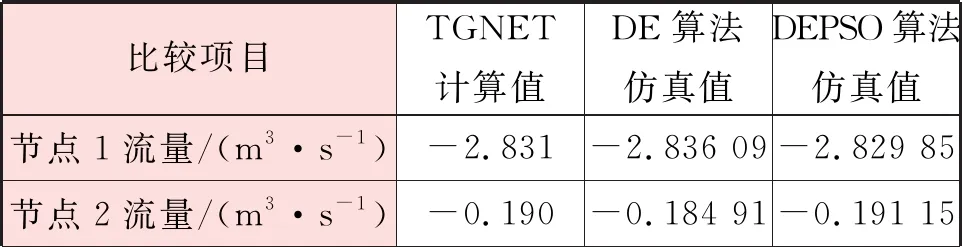
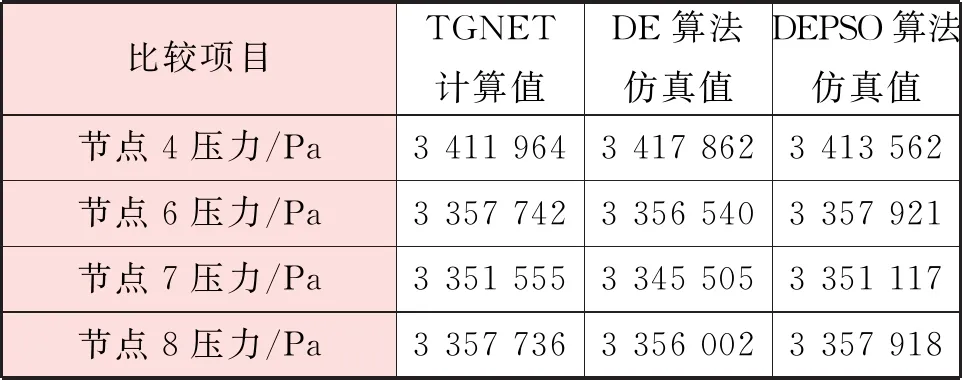
=0.5，设置两个种群数量都为50，最大迭代次数为200代。最终目标函数为0.012。使用DE算法进行对比，种群数量设置为100，其余设置相同，最终目标函数为0.039。辨识结果见表4。工况5计算结果、验证结果分别见表5、6。结果显示，DEPSO算法的结果明显优于DE算法结果，并且辨识后DEPSO算法仿真相对误差绝对值降低至1%以下。

4.3 实际管网阻力辨识验证

本文实际管网数据由上海叁零肆零科技有限公司提供，为东莞某区域次高压管网。该区域共有两个气源点，都为高压管网至次高压管网的调压站。管网共有529根管段，经拓扑结构简化后共有14根管段，其中最大管长为10.5 km，实际管网拓扑结构图见图7。图中节点编号为0～14。

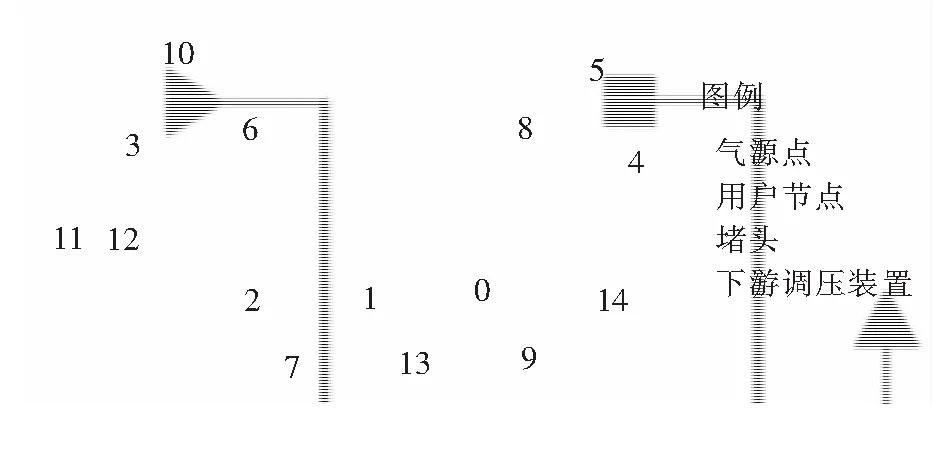
管网中测点包括：节点7、8、10压力以及流量测点；气源点5的压力及流量测点、气源点11的压力测点。

将节点5、7、8、10的节点流量以及节点11的压力作为仿真计算的依据，其余测点参数纳入目标函数之中。实际管网测点数据见表7。表中，节点10、11相距较近,不足200 m。同时仪表测量分度值为1 kPa。因此，两节点压力接近。采用2022年1月5日共24个工况进行方法验证。随机选取0：00、10：00以及13：00工况作为辨识工况，8：00、16：00作为验证工况。DEPSO算法各参数设置与第4.2节中相同。针对辨识工况，目标函数由辨识前的1.62降至辨识后的0.21。针对验证工况，目标函数由辨识前的1.53降至辨识后的0.23，验证工况各测点数据见表8。仿真最大相对误差绝对值由辨识前的0.81%降低至辨识后的0.15%，并且辨识后的仿真结果全部在0.2%的相对误差绝对值范围内。

5 结论

① 针对燃气管道存在跨流态变化以及当量绝对粗糙度不易获取等实际困难，确定辨识参数为管径

，并确定了合理的参考范围为[0.8

,1

2

]，为后续实施优化算法中可行域的确定提供了基础。

② 提出了阻力辨识问题的目标函数，以简单环网为模型，对目标函数的特征进行分析，发现了在全局最优解附近存在狭长的平坦区域这一特征，为后续算法设计提供了基础。

③ 提出一种DEPSO算法用于阻力辨识问题求解，在建立的虚拟管网中进行验证，并与DE算法进行对比，结果显示DEPSO算法辨识的误差更小，验证工况的仿真相对误差绝对值在1%以内。

④ 在实际管网中对阻力辨识方法进行验证，结果显示相较辨识前，仿真误差下降明显，且辨识后仿真结果与实际测量数据相对误差绝对值在0.2%以内。

[ 1 ] 王海,王海鹰,周伟国,等. 供热管网中管段阻力系数的辨识方法[J]. 计算物理,2013(3):422-432.

[ 2 ] 梁静,刘睿,瞿博阳,等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报(工学版),2018(3):15-21.

[ 3 ] 王磊. 基于差分进化算法的管网模型校正[J]. 山西建筑,2009(3):190-191.

[ 4 ] 郭伟. 大规模给水管网微观模型简化与校核方法研究(硕士学位论文)[D]. 哈尔滨：哈尔滨工业大学,2017:38-54.

[ 5 ] 栾丽君,谭立静,牛奔. 一种基于粒子群优化算法和差分进化算法的新型混合全局优化算法[J]. 信息与控制,2007(6):708-714.

[ 6 ] 李净文,李国,徐晨,等. 基于一种自适应选择机制的混合优化算法[J]. 计算机应用研究,2015(2):360-363，375.

[ 7 ] 王兴畏. 城市天然气输配管网水力模拟研究与实践(博士学位论文)[D]. 重庆:重庆大学,2013:19-29.

[ 8 ] HE Shunan，HU Junzhi. Steady state calculation and analysis of long-distance natural gas pipeline network[J]. International Journal of Computational and Engineering，2020(4):248-251.

[ 9 ] KANG D，LANSEY K. Demand and roughness estimation in water distribution systems[J]. Journal of Water Resources Planning & Management，2011(1): 20-30.

[10] 周志刚,邹平华,谈和平,等. 基于遗传蚂蚁混合算法的热网阻力特性辨识[J]. 哈尔滨工业大学学报,2008(11):1761-1765.

[11] 刘永鑫,邹平华,周志刚,等. 基于方程组极小范数解的供热管网阻抗辨识方法[J]. 暖通空调,2011(2):80-84.

[12] ELTAEIB T，MAHMOOD A. Differential evolution: a survey and analysis[J]. Applied Sciences，2018(10):1-25.

[13] STORN R，PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization，1997(4):341-359.

[14] 杨维,李歧强. 粒子群优化算法综述[J]. 中国工程科学,2004(5):87-94.

[15] 胡乃平,宋世芳. 一种局部与全局相结合的微粒群优化算法[J]. 计算机工程，2008(17):205-207，210.