全尺寸巷/隧道火灾风烟流温度预测模型与验证*
2022-09-21康建宏周福宝雷柏伟
李 晴,康建宏,2,周福宝,3,雷柏伟
(1.中国矿业大学 安全工程学院,江苏 徐州 221116; 2.江苏省城市地下空间火灾防护高校重点实验室,江苏 徐州 221116;3.中国安全生产科学研究院,北京100012; 4.中国矿业大学(北京) 应急管理与安全工程学院,北京 100083)
0 引言
隧道是现代城市重要交通设施,是改善运输条件有效手段。隧道交通在给生活带来便利同时,隧道火灾事故也造成了重大损失。随着隧道长度和数量增加、车流密度和速度增加,隧道火灾事故发生频率也随之增加,给隧道消防安全带来了巨大的挑战[1-2]。
目前,针对巷/隧道火灾的热动力灾害行为、烟气蔓延特性以及温度分布等,很多学者开展了一系列小尺寸实验研究。李炎锋等[3]在6.6 m×1.3 m×1.5 m(长×宽×高)的中尺度隧道内实验,研究不同通风条件下坡度对烟气蔓延速度的影响规律。杨健等[4]在1/20的缩尺隧道内探究通风风速对不同燃烧物和隧道截面尺寸下顶棚最大烟气温升的影响,建立了火源上游无量纲温升与距离的相关关系。梁强等[5]基于小尺寸狭长通道实验平台,监测汽油燃烧产物浓度变化和烟气温度分布情况。马砺等[6]理论分析了封堵行为对烟气质量流率的卷吸作用,并实验观测了不同封堵比例下烟气温度特性,构建了考虑封堵率影响下烟气温度纵向衰减的预测模型。
尽管小尺寸实验在揭示火灾机理方面发挥了重要作用,但是由于其无法“再现”复杂的实际巷道条件,在指导工程实践方面存在一定的局限性。因此,开展大尺寸尤其是全尺寸实验尤为重要。傅培舫等[7]在贴合实际条件的实验巷道中开展燃烧测试,监测火灾时期燃烧区热阻力与热动力的变化关系。胡隆华[8]在3种大型公路隧道中开展油池火实验,研究烟气一维扩散过程中沿隧道顶板的分布,建立了不同通风速度下CO浓度和烟气最大温度的纵向衰减模型。王彦富等[9]在全尺寸巷道中实验研究火源上游烟气逆流特性,建立了预测烟气逆流长度的计算模型。史聪灵等[10-11]分别在地铁区间隧道和车站隧道进行全尺寸甲醇燃烧实验,研究通风排烟系统开启下烟气扩散规律以及温度变化情况。孙少华等[12]实验探究了机械通风速度对火源热释放速率、烟气温度以及燃烧产物成分的影响。
以上有关全尺寸巷/隧道火灾研究大多关注于烟气输运特性和温度纵向分布,较少考虑到烟气温度随时间的演化规律,且缺乏相关的预测模型。本文基于能量守恒定律和热量转换关系,建立巷/隧道火灾风烟流温度演化的预测模型,并通过开展全尺寸巷道火灾实验以及将实验结果与几个典型隧道火灾实验数据对比,对理论模型进行验证。研究结果可为巷/隧道火灾时期的烟气控制和救援提供理论参考。
1 巷/隧道火灾风烟流温度预测模型
1.1 直巷内烟流温度预测模型
巷道发生火灾时,整个燃烧过程处于完全紊流的状态。用单位时间内燃料的消耗量来表示燃料消耗率mr,引入比燃料消耗率k(t),其定义为燃料消耗率mr与进风量m0的比值。单位时间内燃料燃烧的总产热量E计算如式(1)~(2)所示:
E=mrq=m0k(t)q
(1)
其中,
m0=ρQ
(2)
式(1)中:mr为燃料消耗率,kg/s;q为燃料热值,J/kg;k(t)为t时间内燃料消耗率;t为燃烧时间,s;m0为进风质量流量,kg/s。
式(2)中:ρ为空气密度,kg/m3;Q为进风体积流量,m3/s。
根据文献[13]对不同燃料和通风条件下的火灾实测数据,比燃料消耗率随燃烧时间的变化规律可用式(3)描述:
(3)
式中:m为燃烧物的质量,kg。
燃料燃烧释放的能量使空气、烟气以及燃烧产物从常温升到高温,且气体的比热容受温度的影响较小,因而气体的焓增由式(4)计算:
ΔH=CpρQ(T-T0)
(4)
式中:Cp为空气的定压比热容,J/(kg·K);T为烟流温度,K;T0为巷道初始温度,K。
火灾烟流与壁面之间对流换热是一个包含自然对流与强迫对流的复杂过程,其对流换热系数α可以由式(5)计算[14]:
α=kQ0.8U0.2S-1
(5)
式中:α为对流换热系数,W/(m2·K);U为巷道周长,m;S为巷道截面积,m2;k为对流换热系数常量,依据井下煤和岩石的导热系数[15],结合量纲分析得到:岩巷中对流换热系数常量范围为10~46,煤巷中对流换热系数常量范围为58~94,本文计算取中间值。
烟气与巷/隧道壁面及环境之间热交换功率可由式(6)计算:
(6)
式中:qr为对流换热功率,W;x为烟流蔓延到的位置与火源的距离,m。
燃料燃烧释放的能量绝大部分用于气体的焓增以及与巷/隧道边界和环境之间热交换功率,即式(7):
E=ΔH+qr
(7)
把式(1)、式(4)和式(6)带入到式(7)中,得到直巷/隧道火灾时期风烟流温度演化的预测模型表达式如式(8)所示:
(8)
1.2 分叉和汇合巷道内的烟流温度预测模型
巷道的分叉和汇合直接影响烟气蔓延和温度变化,在图1所示的分叉巷道中,发火巷道中烟流经过分叉点后进入其他巷道,忽略分叉点处的局部损失,温度的改变主要受巷道风量、巷道尺寸以及蔓延距离的影响,此时气体的焓增不变,烟气蔓延到巷道n中A位置处的对流换热量由式(9)表示:
qA=k[Q0.8×U1.2x1S-1+Qn0.8×Un1.2x2Sn-1)(TA-T0)
(9)
式中:Q和Qn分别为发火巷道和巷道n上的风量,m3/s;U和Un分别为发火巷道和巷道n的周长,m;S和Sn分别为发火巷道和巷道n的面积,m2;x1为分叉点到火源的距离,m;x2为A位置到分叉点的距离,m;TA为A位置处的烟流温度,K。
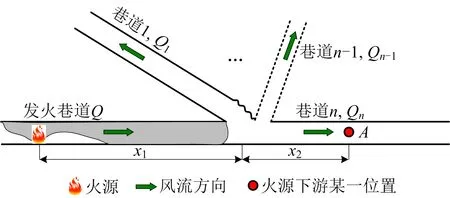
图1 分叉巷道示意Fig.1 Schematic diagram of bifurcation roadway
由式(8)得巷道n中A位置处的烟流温度变化为式(10)所示:
(10)
如图2所示的汇合巷道,当发火巷道的烟流与其他巷道风流在井巷交叉点处混合时,假设在汇合点处各组分达到完全均匀混合,风温达到平衡,忽略汇合点处局部损失,此时空气的焓增为加热发火巷道和其他巷道内空气和燃烧产物所需能量之和,见式(11)所示:
(11)
式中:Qi和Qj分别是巷道i(i=1,2,…,j-1)和巷道j上的风量。
烟气蔓延到巷道j中B位置处的对流换热量由式(12)表示:
qB=k[Q0.8×U1.2x3S-1+Qj0.8×Uj1.2x4Sj-1)(TB-T0)
(12)
式中:Uj为巷道j的周长,m;Sj为巷道j的面积,m2;x3为汇合点到火源的距离,m;x4为B位置到汇合点的距离,m;TB为B位置处的烟流温度,K。
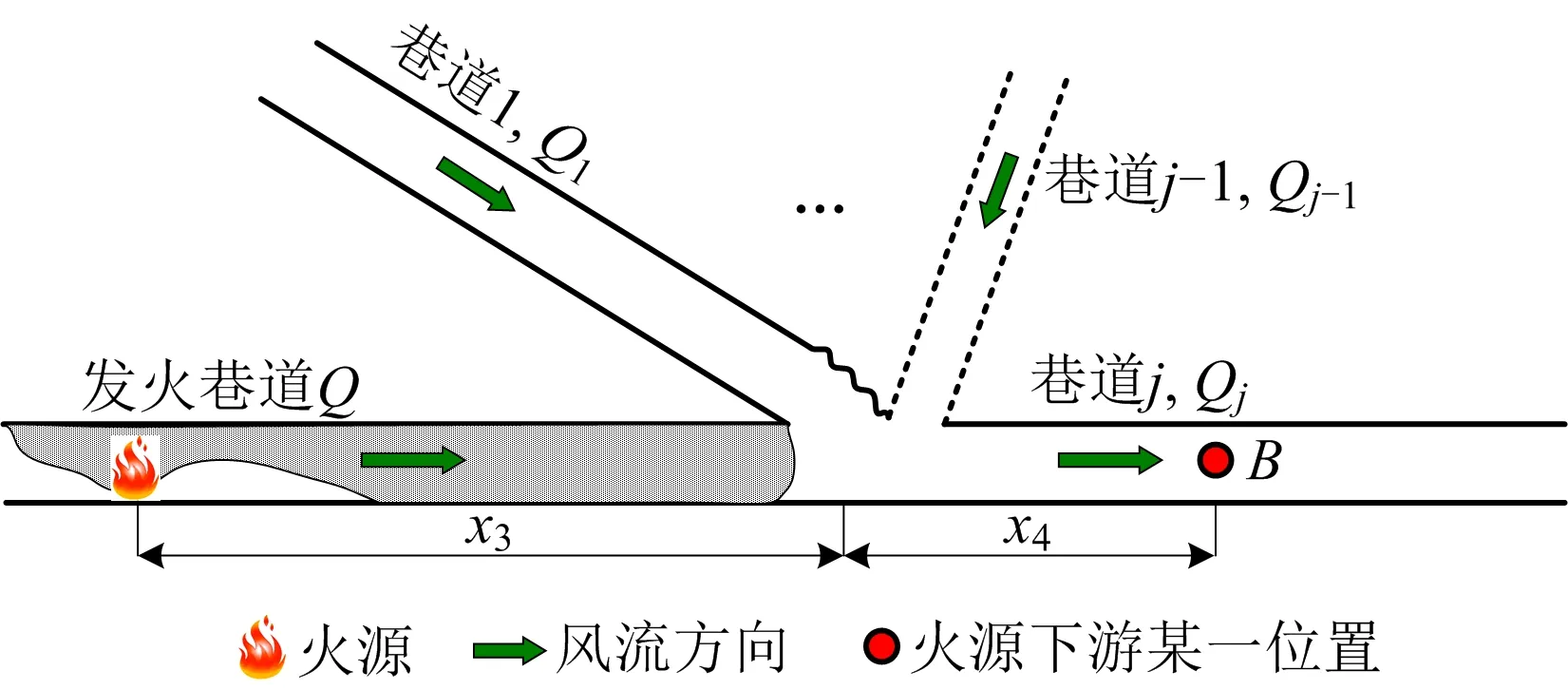
图2 汇合巷道示意Fig.2 Schematic diagram of confluence roadway
由式(8)得巷道j中B位置处的烟流温度变化如式(13)所示:
(13)
从式(8)、式(10)和式(13)可以看出,烟流温度演化模型T(x,t)是时间和距离的函数,巷/隧道发生火灾,火源下游某一位置,某一时刻的烟流温度可通过计算得到。
2 全尺寸巷道火灾实验
2.1 国家矿山应急救援开滦队实验巷道布置
如图3所示,在国家矿山应急救援开滦队开展的全尺寸巷道实验,火源所在的进风巷道长69 m,截面上半部分为直径3.2 m的半圆形,下半部分为长3.2 m、高0.8 m的矩形。巷道采用负压抽出式通风,火源所在进风巷风量为434 m3/min,风速为0.9 m/s。
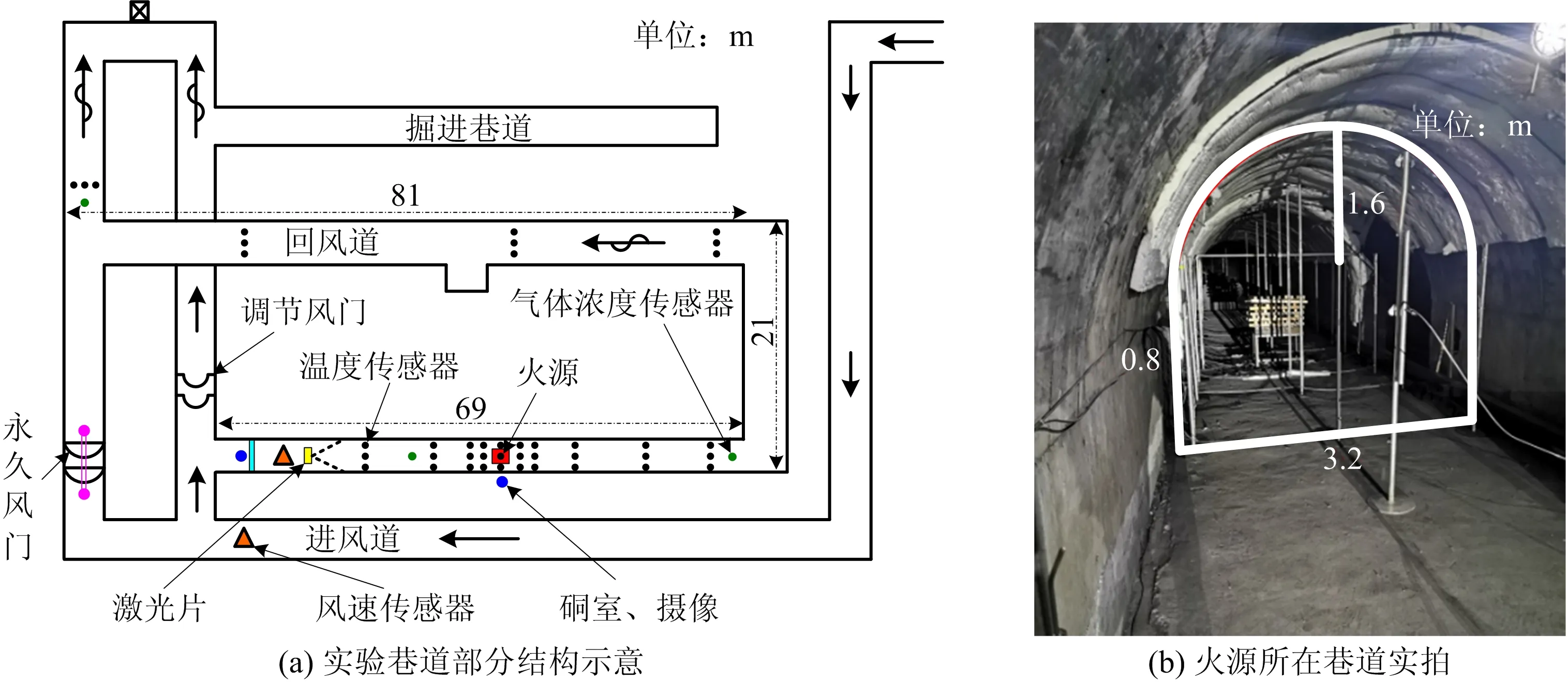
图3 国家矿山应急救援开滦队实验巷道布置Fig.3 Layout of test roadways in national mine emergency rescue Kailuan team
实验燃烧材料为木材,由尺寸为长0.8 m、宽0.04 m的木条搭建成0.8 m×0.8 m×0.4 m(长×宽×高)的木垛,木垛总质量为45 kg,放置在金属托盘上,托盘由金属支架垫起离地0.4 m,置于进风巷道中心处。在距离火源不同位置的上、下游截面上布置烟气温度传感器,每个截面设有13个热电偶用于监测不同高度层的烟气温度。此外,巷道内安装气体浓度传感器和风速传感器,实时记录木垛燃烧产生的CO2浓度变化以及巷道内的风速值,传感器具体位置见图3(a)所示。实验开始时首先引燃底部木材,利用放置在火源上游的激光片观察火势发展过程,并观察火灾烟气运移情况。
2.2 国内其他全尺寸巷道实验条件
傅培舫[13]在重庆煤科院分院通风实验巷道内开展了14次燃烧实验,选择井下可能的易燃物作为火源,以堆积布置、沿长均匀布置等分布方式模拟点火源、线火源以及皮带运输机火灾,探究不同燃烧物质、燃烧规模和通风条件下燃烧产物的热物理参数变化和风烟流演化规律。胡隆华[8]在大风垭口隧道和元江1#隧道开展6次全尺寸火灾实验,以汽油为燃料,通过风机提供纵向风速,研究不同火源热释放速率下隧道内的顶棚最大烟气温度和温度纵向分布规律。表1中列出了在重庆煤科分院的通风实验巷道、大风垭口实验隧道以及元江1#实验隧道开展全尺寸实验的部分实验条件,包含:隧道尺寸、燃烧物种类、燃烧物质量、热值以及纵向通风速度。
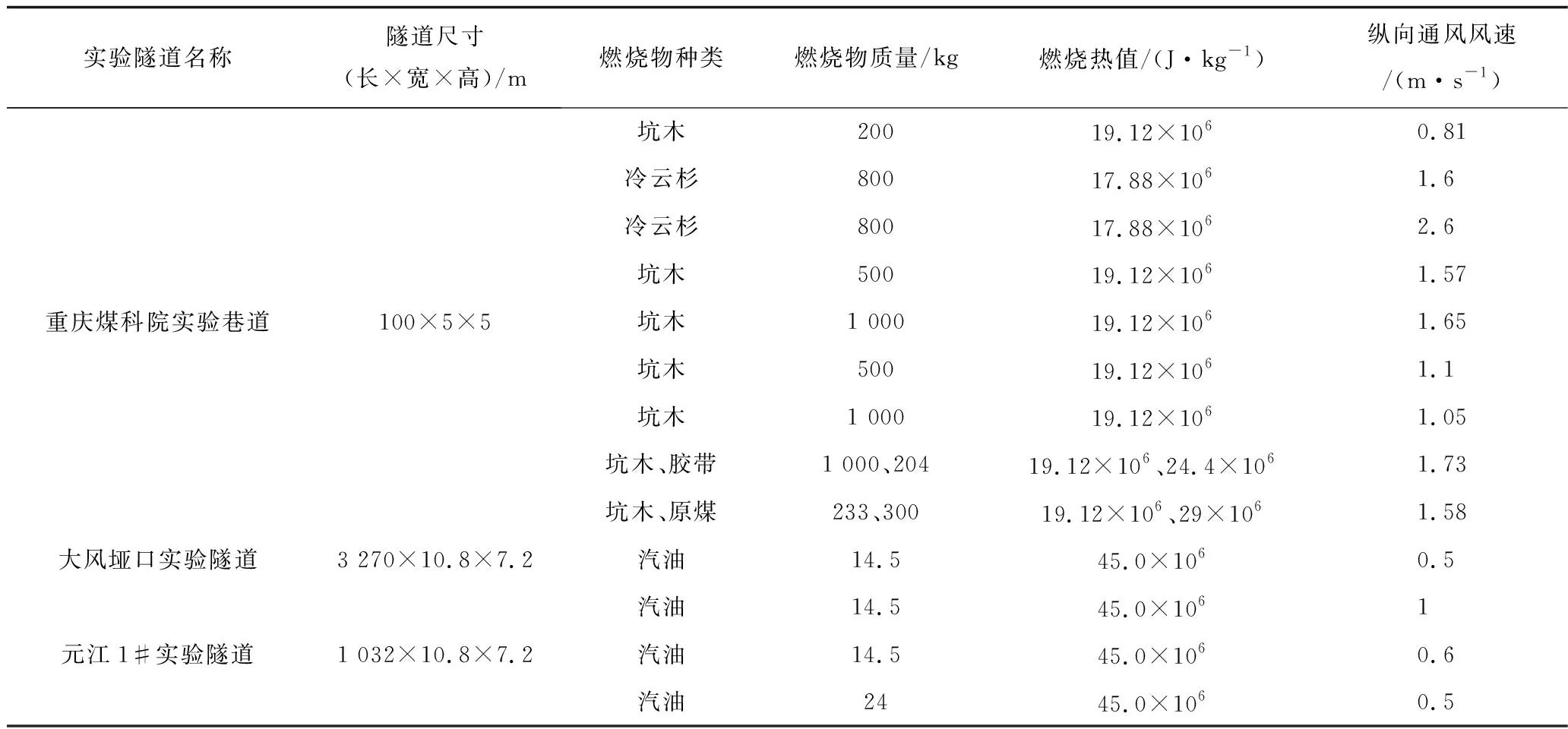
表1 不同隧道各次火灾实验初始条件Table 1 Initial conditions of each fire test in different tunnels
3 结果与讨论
图4呈现了在开滦实验巷道开展的全尺寸火灾实验中,火焰燃烧的发展阶段和稳定阶段。稳定阶段火势达到最大,此时火源功率最大,产生更多烟气,且烟气分层现象明显。图5展示了位于火源上、下游8 m处截面上的烟气温度分布情况。可以发现:纵向通风对火源两侧烟气温度有较大影响,上游8 m截面中心线上烟气最高温度从2.2 m高度上的216 ℃,降至1.0 m高度上的33 ℃,而在火源下游8 m处的截面中心线上,烟气最高温度从2.2 m高度上的262 ℃,降至1.0 m高度上的49 ℃。

图4 不同阶段火焰燃烧状态Fig.4 Flame combustion state at different stages
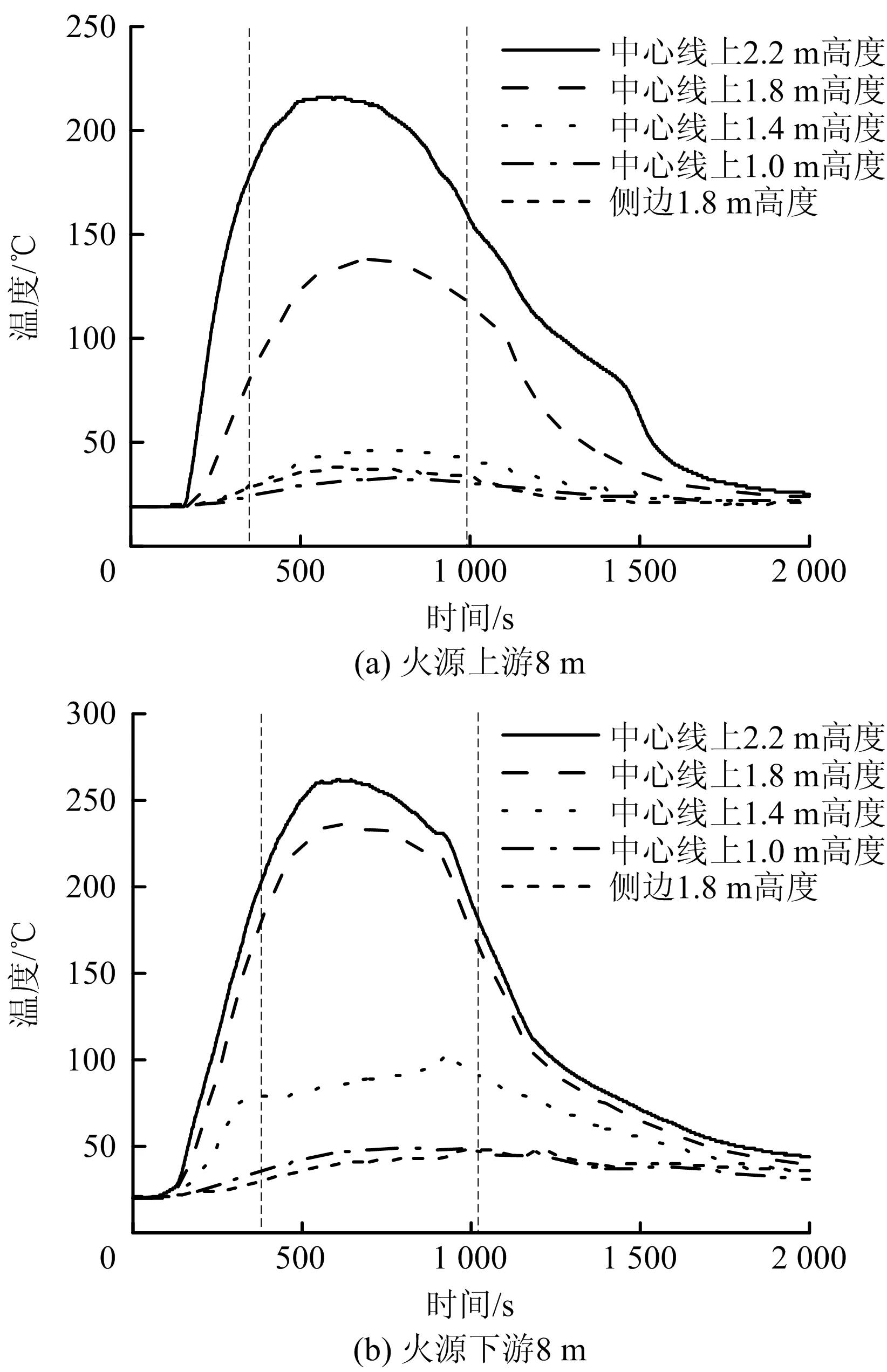
图5 距离火源不同位置截面上的烟气温度分布情况Fig.5 Smoke temperature distribution on cross sections at different locations away from fire source
图6展示了距离火源不同位置处巷道顶棚烟气温度随燃烧时间变化的理论计算和开滦实验数据的对比,二者的变化趋势基本一致,都有温度迅速上升的发展阶段、达到最大温度的稳定阶段及温度缓慢下降的衰减阶段,该变化趋势符合火灾火源燃烧特性曲线[16]。实验数据相比理论结果,实际燃烧中的稳定阶段维持时间较长,且火区附近烟气温度衰减较慢,这是因为在实际燃烧过程中,持续燃烧的火焰对近火源区域空气的加热使得热量散失得慢,温度不易降低,且巷壁围岩的储热能力大,对巷道起到一定的保温作用。燃料燃烧产生的烟气在浮力的驱动下向上运动,碰到顶板后沿着隧道纵向蔓延,因而距离火源越远,顶棚烟气达到最大温度的时间越长。图6所示的实验数据中,火源正上方和距离火源20 m位置烟温达到峰值的时间分别约为7 min和11 min。烟气在纵向蔓延的过程中由于热阻力和能量交换,温度持续衰减,最大温度应在火源正上方。而在实验巷道中,由于纵向通风的作用,烟气受到的热动力小于纵向通风提供的动压,火源上方的烟气向下风侧偏离,导致最大温度出现在火源下游1 m的位置,如图7所示。烟气最高温度沿巷道纵向衰减的理论计算和实验结果大致相符,理论计算与实验数据的误差在9%以内。
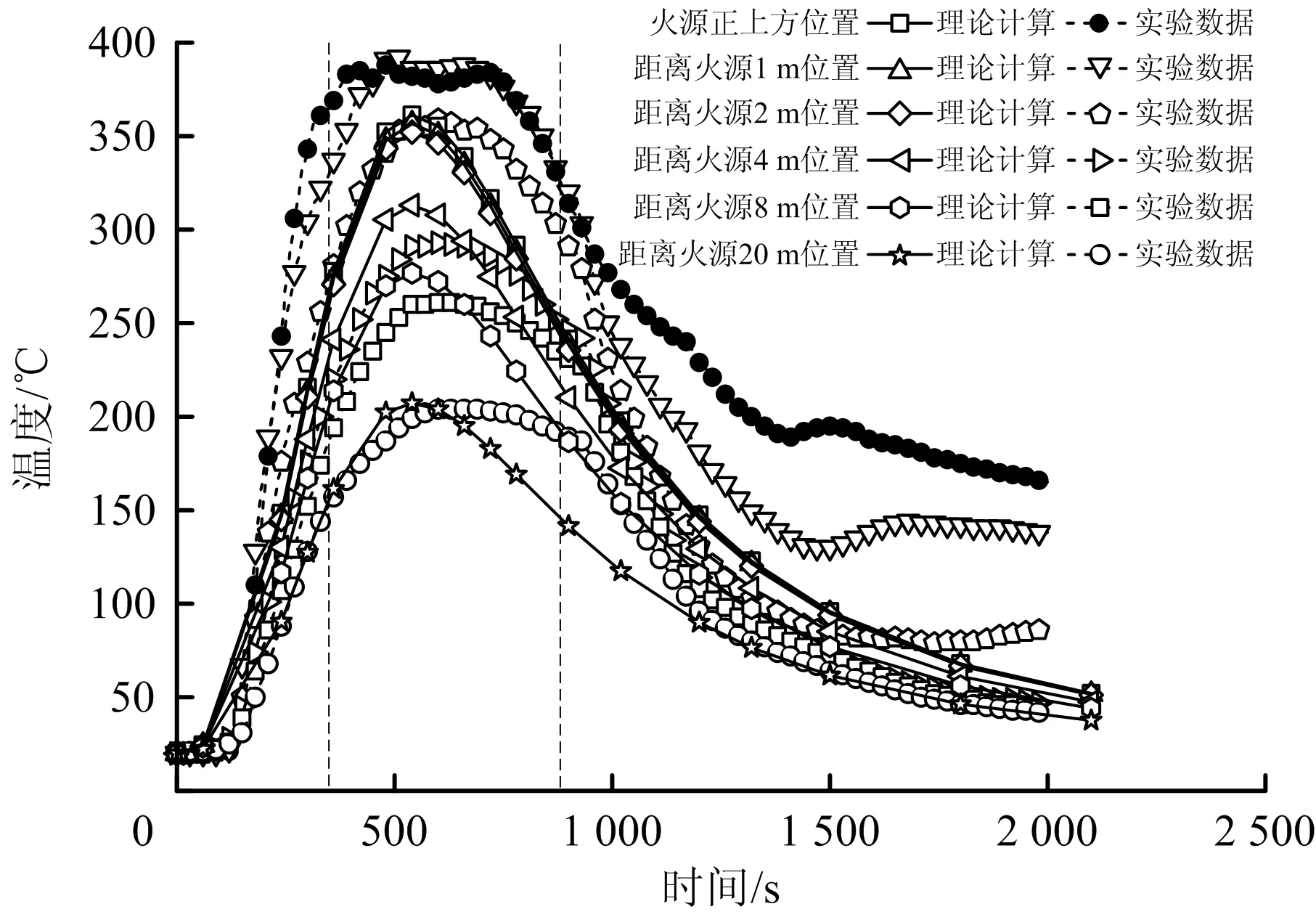
图6 烟流温度随时间变化的理论计算和实验数据对比Fig.6 Comparison between theoretical calculation and experimental data on variation of smoke flow temperature with time
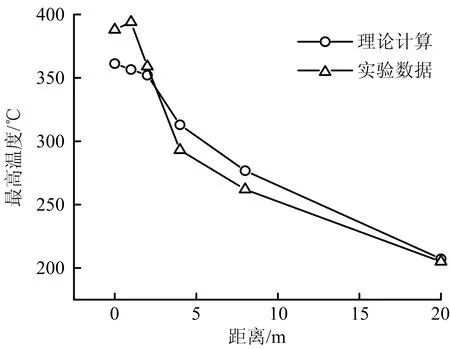
图7 烟流最高温度随距离变化的理论计算和实验数据对比Fig.7 Comparison between theoretical calculation and experimental data on variation of maximum smoke flow temperature with distance
图8所示在重庆煤科分院通风实验巷道在第3次实验条件下(用800 kg的冷云杉作为燃烧物,纵向通风速度为2.6 m/s),距离火源不同位置处烟流温度随随时间变化的理论计算和实验数据对比,可以看到二者的变化趋势基本一致。图9中烟气最高温度的理论值和实验值的误差率最小约为3%,最大不超过14%。需要指出的是:距离火源96 m和114 m的温度测点布置在燃烧巷道与主巷道汇合后的巷道中,此位置处的温度变化通过公式(13)获得。
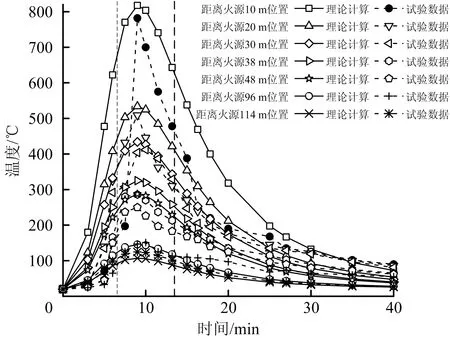
图8 重庆煤科分院通风实验巷道在第3次实验条件下烟流温度随时间变化的理论计算和实验数据对比Fig.8 Comparison between theoretical calculation and test data on variation of smoke flow temperature with time of ventilation experimental roadway of Chongqing Coal Science Research Institute under the third experimental conditions
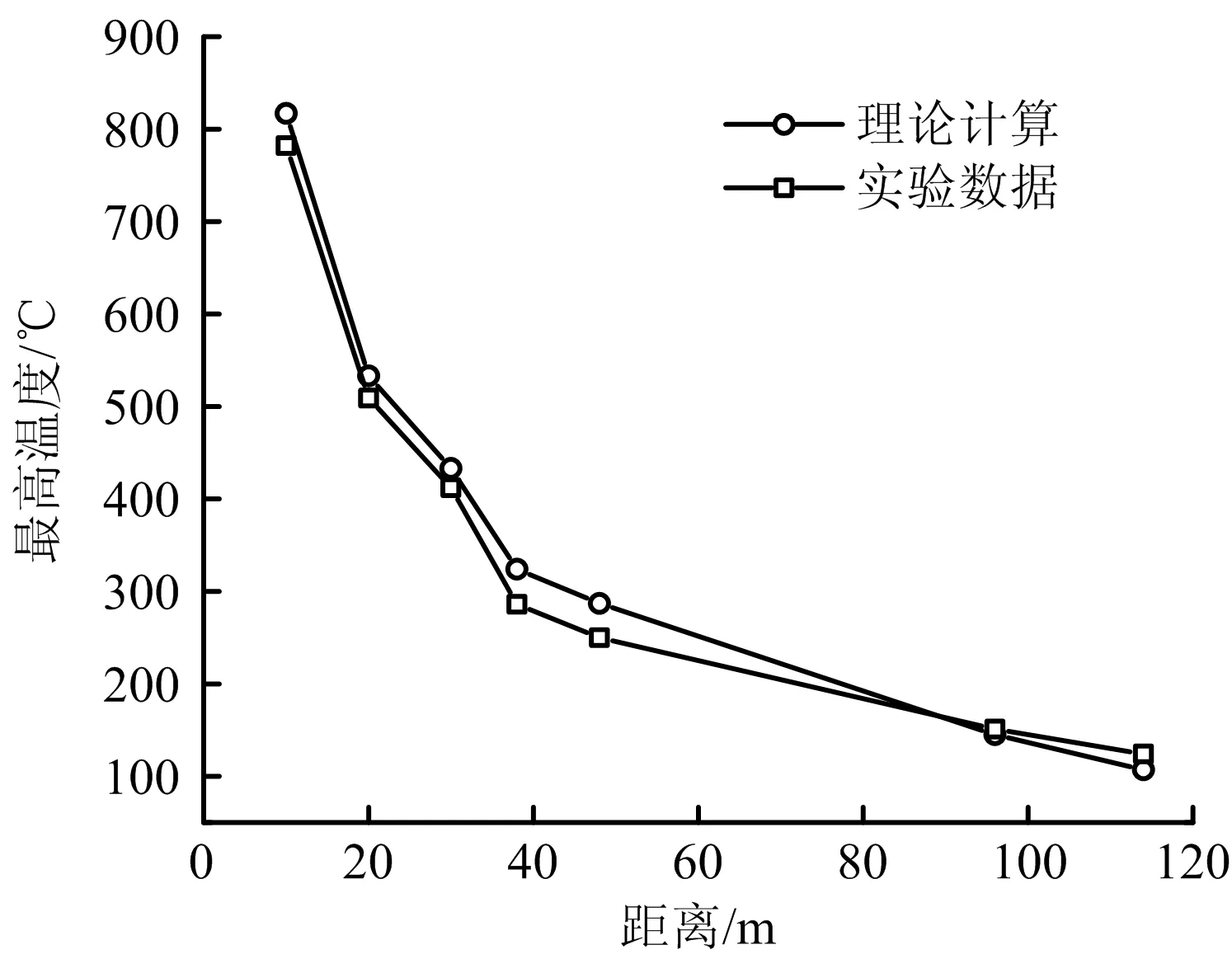
图9 重庆煤科分院通风实验巷道在第3次实验条件下烟流最高温度随距离变化的理论计算和实验数据对比Fig.9 Comparison between theoretical calculation and test data on variation of maximum smoke flow temperature with distance of ventilation experimental roadway of Chongqing Coal Science Research Institute under the third experimental conditions
如图10所示,在重庆煤科分院的通风实验巷道开展的如表1所列的各次实验条件下火源顶棚最高温度实测数据和通过式(8)计算得到的理论值进行对比。可以发现:通过理论计算得到的温度最大值与实验数据结果大致相符,其误差率基本稳定在5%以下。
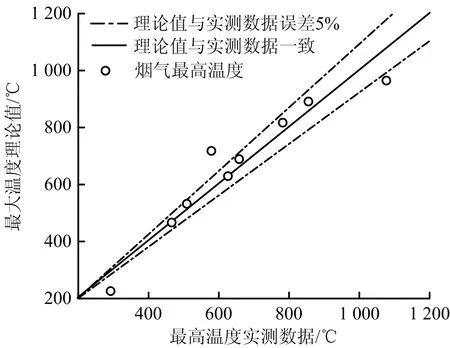
图10 重庆煤科分院通风实验巷道在各次实验条件下火源顶棚最高温度的理论值和实测数据对比Fig.10 Comparison between theoretical values and measured data of ceiling maximum temperature above fire source of ventilation experimental roadway of Chongqing Coal Science Research Institute under various experimental conditions
为了验证分叉巷道内烟流温度预测模型的准确性,引入Chen等[17]在分叉隧道内开展的实验结果与理论模型对比。如图11所示,当主巷道风速为0.2 m/s和0.6 m/s时,通过公式(10)计算的烟流温度理论计算值与实验数据对比,二者具有较好的一致性,说明公式(10)一定程度上可以预测分叉巷道内烟流温度变化。
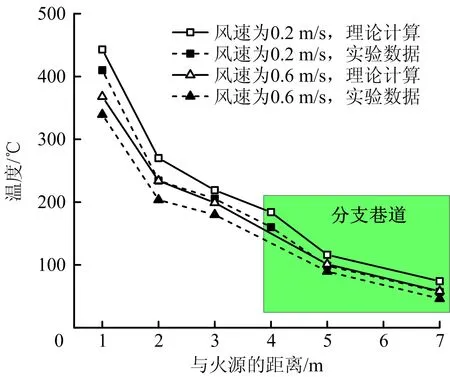
图11 通过公式(10)计算的理论结果与实验数据的对比Fig.11 Comparison between theoretical results calculated by formula (10) and experimental data
从图12所示的烟气温度沿巷道纵向衰减的理论结果与重庆煤科分院通风实验巷道、大风垭口实验隧道以及元江1#实验隧道全尺寸实验数据的对比结果可知,火灾烟气温度演化的理论模型可以给出预测结果。大风垭口实验隧道和元江1#实验隧道的实验数据与理论值有相对较大的偏差,分析可能的原因如下:理论模型的建立是基于矿井火灾实测数据,其燃烧物多为坑木、胶带等,燃烧不充分且燃料消耗率较低,而在大风垭口实验隧道和元江1#实验隧道开展实验所用的燃料是燃烧效率较高的汽油,会产生更多的热量,燃料的燃烧效率不同是导致预测结果偏差的主要原因。总体上实验数据与理论计算结果较为吻合,该理论模型可以描述烟气温度在巷道内的纵向衰减情况。
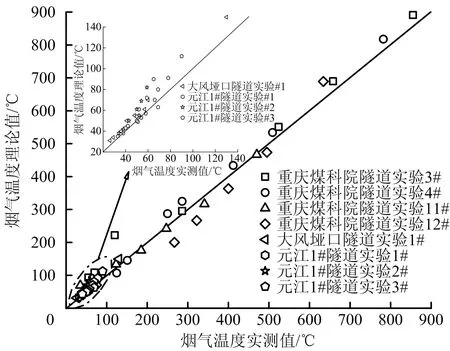
图12 烟气温度沿巷道衰减的理论值和实验数据对比Fig.12 Comparison between theoretical values and experimental data of smoke temperature attenuation along roadway
4 结论
1)巷/隧道火灾风烟流温度预测模型所呈现的烟气温度随时间的变化关系,可以反映火灾发展的3个阶段,且烟气温度的变化趋势基本符合火灾火源燃烧特性曲线。
2)理论模型能够预测顶棚最大烟气温升以及温度纵向衰减现象,烟气最高温度的预测值与实验结果的误差率在15 %以内。
