分布式光伏接入的配电网无功优化研究

福建永福电力设计股份有限公司 王智聪

引言

全球气候变暖，资源和环境面临重大威胁，提高能源利用率、改善能源结构、寻求可再生资源是世界各国面临的首要问题。现阶段，分布式电源（Distributed Generation，DG）技术是我国清洁能源利用的主要形式，其PV是DG 的重要代表，PV 应用以接入配电网为主，一旦PV 接入配电网方式不当将会引起诸多问题，例如电压越限、电压波动和谐波污染等，对配电网的规划预测以及优化控制带来了极大的挑战，十分不利于配电网的高效、安全稳定运行，因此要对PV接入配电网进行合理研究规划，提出适用于PV 接入的配电网无功优化原理和方法，来更高的引导对PV 的合理规划和应用，保证电网的安全稳定运行。

分布式光伏电源（Distributed Photovoltaic Power,PV）接入电网后配电网的潮流分布发生了改变，影响了系统网络的安全性和可靠性，因此开展对含PV 的配电网无功优化研究十分关键，对提升电网运行稳定性与高效性具有重要意义。文章介绍配网中并入分布式光伏后无功优化的研究现状，阐述分布式光伏接入配电网的模型和控制策略，介绍优化算法在含分布式光伏接入的配电网无功优化中的应用，旨在为相关研究提供理论借鉴。

1 配网中并入分布式光伏后无功优化意义及现状分析

1.1 配网中并入分布式光伏后无功优化的意义

PV 并网后对配网的潮流分布所产生的不确定性的改变是一个重要的技术问题，在线路传输过程中，有功功率保证了用户的实际用电，无功功率用于维持电压的稳定。但是如果无功功率过高，在远距离传输上会导致网络损耗加大，加大功率损耗，甚至还会造成末端电压越限，容易引发电网安全事故。因此，对PV 并网后配电网的无功优化研究具有重要的现实意义，一方面提升电压稳定性、降低网络损耗；另一方面可增大网络传输容量，保证了电网的安全、高效、稳定运行，实现电网的经济可持续发展。

1.2 配网中并入分布式光伏后无功优化的研究现状

分布式光伏具有较大的随机波动性，会致接入容量不稳定，发生系统有功和无功大小不定甚至改变潮流走向，造成配电网的无功优化更加困难。PV接入配电网的无功优化可通过多种方式进行补偿，传统的补偿方式如改变变压器分接头、安装调相机、电容器等补偿装置等，实现对无功补偿容量的调控，达到降低网网损、减小系统电压偏差的目的，但通常变压器分接头的调节次数难以任意调节，局限性较大；电容器补偿设备只适用于负荷稳定的低压力系统中；调相机存在投资大、维护费用高的问题。

为了解决这一系列问题，引入了现代无功补偿装置，其中代表性的有静止无功补偿器（简称“SVC”）和静止无功发生器（简称“SVG”），通过利用半控型晶闸管控制补偿设备的投退，来实现对系统无功补偿大小的改变。大量研究证实，通过加入SVC 和SVG 补偿后，有效提升了新能源并网变换器的极限输出功率。

无功功率优化过程是动态变化的，并且还有一部分是离散过程，约束条件多、影响因素复杂，寻优计算难度大。目前配电网无功优化算法种类繁多，传统应用的算法主要有线性规划法、牛顿法等，但通常建模较难，而粒子群算法（简称“PSO”）[1]具有自适应性强、灵活方便等特性，可更好的优化配电网无功优化。

通过在对分布式光伏接入配电网的运营模型优化过程中，采用多目标粒子群优化算法完成，有效克服算法易陷入局部最优等缺点，利用小生境技术对算法加以改进[2]，为保证PV 接入配网后系统能更加稳定的运行，在PV 接入配网后，需要对电压偏差最小、网络损耗最小等多个目标函数同时进行优化，保证优化过程解的多样性，防止算法早熟收敛。拥挤距离排序法形成每个粒子的小生境，采用小生境共享机制更新粒子位置提高粒子适应度，同时在全局最好位置的选择时与外部档案维护结合，实现对配电网电压、网损的有效控制和管理。

2 分布式光伏接入配电网的模型

光伏发电的能量转换是通过光伏电池板将太阳能转化为直流电能，再通过控制器转换为交流电并入电网供用户使用。可见光的辐射量和环境温度是影响能量转换的重要因素，但通常这两个因素的随机性较强，导致光伏电源发电的有功和无功出力不确定性较高，光伏发电系统模型的建立有直接模型和间接模型，直接建模需要大量数据来支撑，但对于分布式电源数据的统计是难点，因此现阶段主要采用间接模型实现对光伏发电系统建模。

一般而言，光照强度、温度、电池板面积是影响光伏系统出力的重要因素，光伏的出力情况符合负荷“昼高夜低”的特性。光伏电源模型可视为Beta 分布，概率密度函数为[3,4]：f(P)=τ(α+β)/(τ(a)τ(β))×(L/Lmax)α-1×(1-L/Lmax)β-1，此式中：τ 为Gamma 的函数；α、β 为形状参数；L 为这一时间内实际光照强度；Lmax为这一时间段内的最大光照强度）。其中，β=(1-μ)×[(μ(1+μ))/σ2-1]，α=(μ×β)/(1-μ)，式中：μ 为平均光照强度，σ2为方差。

建立分布式光伏有功出力概率模型为：fb(P)=τ(α+β)/(τ(α)τ(β))×(P/Pmax)α-1×(1-P/Pmax)β-1，式中：P 为系统的有功功率，Pmax为最大有功功率。无功功率为：Q=Ptanφ，式中：Q 为系统的有功功率，φ 为功率因数角。

3 分布式光伏接入配电网的控制策略

在实际情况下，为了降低运营成本，在光伏并网时要利用逆变器的无功容量及调节能力。在白天时，允许PV 适当发出一部分无功功率来平衡从电网吸收的无功功率，可有效降低光伏并网成本，还可以实现在接入点电压较低时来达到维持电压稳定的目的。可见要对其逆变器的无功输出进行合理控制，主要控制策略如下。

有功调整功率因数控制。该控制方式是基于不同时刻有功功率大小来对cosφ 进行调节，其中cosφ（P）控制策略示意图如图1所示。可看出，当PV 有功出力小于Pmin，功率因数以最大值运行；当PV 有功出力大于Pmax，功率因数以最小值运行；介于二者之间时，cosφ 随着有功功率出力的增大而减小。

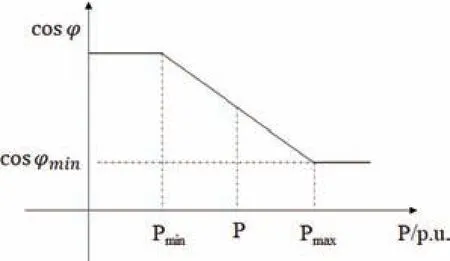
图1 cosφ（P）控制策略示意图

并网点电压调整无功功率控制。在基于该控制方式下，可通过不同时刻网络中各节点电压值偏离情况来确定无功出力大小，其Q(U)控制策略示意图如图2所示。可看出，当电压超出上下限则为不合格区域，以防电压越限，保持最大的无功注入；当接入点电压位于1.05和0.95区间内，该区间为合格电压区域，该区域需要由接入点的电压要求来定量调控无功输出；可见在该控制方式下，逆变器的无功输出只与接入点的电压值相关。

图2 Q(U)控制策略示意图

并网点电压-功率协同控制。采用电压功率协同控制cos(U,P)，要确定并网点的电压水平，在确定功率因数，最后确定cosφmin的值。由图3（图中cosφmin为U 曲线，cosφ 为P 曲线）可见，在电压大于1.02p.u.时，功率因数位于坐标轴以下区域，PV 进相运行吸收无功功率，随着有功功率的加大cosφ 随之降低，吸收的无功功率增大，导致电压有效的降低；当电压小于0.98p.u.时，功率因数位于坐标轴以上区域，功率因素滞后，电压能升高，并且随着有功功率增大，cosφ 随之增大、无功功率随之减小，避免了电压越限的情况。

图3 cos(U,P) 控制曲线

4 粒子群优化算法在含分布式光伏接入的配电网无功优化中的应用

4.1 粒子群优化算法发展概况

粒子群优化算法是智能优化算法的重要代表，其原理是通过模拟鸟群觅食行为来寻求最优路径的方式，该方法无需交叉、变异等繁琐的操作流程，逻辑运算过程简单明了，算法寻优过程目标易于实现，更重要的是可以进行全局随机寻优，寻优过程中粒子位置代表了待寻优结果的数值，通过设定粒子位置的规则更新粒子的最优位置，并以此来获得更优的解。

近年越来越多的研究人员通过对粒子群算法进行优化改进来满足实际应用中需求，多目标粒子群算法的收敛精度低、易早熟等问题是解决的重点，通过对多目标粒子群算法进行改进，采用小生境技术对求解过程加以优化，根据粒子间距来划分小生境，采用共享机制提升粒子的适应度，保证了小生境间的相互独立性，保证算法在搜索中向着最优方向搜索，解决了算法在寻优过程中易陷入局部最优的弊端[5]。

4.2 粒子群优化算法在配电网无功优化应用实例分析

建立模型。为了验证粒子群优化算法在含分布式光伏的配电网无功优化中的有效性，以IEEE33节点配电系统进行计算分析，分布式光伏并网容量为1MW，功率因数值区间[-0.95，0.95]，在10、15、20、31节点增加4个PV，假设线路参数不变，IEEE33节点配电系统示意图如图4所示。

图4 IEEE33节点配电系统示意图

仿真计算。采用粒子群算法对以上阐述的四种不同光伏逆变器出力控制策略与无控制策略下的出力情况进行计算仿真分析，得出不同控制策略下的网络损耗（MW ▪h）大小如下：cosφ（U、P）2.82、Q（U）3.00、cosφ（P）3.20、cosφ3.25、无控制4.62。由此可以看出，在保持其他参数不变下，当光伏逆变器不采用任何控制测试下网络损耗值最大，而采用基于cosφ（U、P）的控制策略进行无功补偿时，其优化后网络损耗值最小，具有一定的经济性。

5 结语

大量分布式光伏接入电网使得电力系统无功优化变得更加复杂，因此采取合理的方法处理PV 出力的不确定性问题尤为重要，求解多目标函数以及运用合适的优化算法是进行含有PV 的配电网无功优化的关键所在。今后在基于现代智能技术的发展下，研究人员应继续对优化算法展开深入研究，不断将新算法引入到配电网无功优化应用当中来寻找一种最佳的优化算法，实现电网的安全稳定性与经济性能的同步提升。