用强度折减法对岩质高边坡稳定性的影响因素分析
2022-09-20张基鹏任伟中余忠祥符贵军舒天白
张基鹏 任伟中 余忠祥 符贵军 舒天白
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.中国科学院武汉岩土力学研究所,湖北 武汉 430000)
随着我国现代化基础建设的快速发展,人们逐渐意识到治理灾害工程的重要性,其中岩质陡立高边坡的失稳破坏在边坡治理工程中较为常见.如位于西南地区某水电工程,岸坡地质条件复杂,岸坡高陡,岩体卸荷深度大,岩体松弛破碎,在开挖条件下出现大变形现象,边坡极易发生失稳[1];元磨高速公路试验段高边坡,节理裂隙发育,岩体破碎,边坡开挖后,裂面张开,地下水渗入裂隙,直接影响该公路段的安全性能[2].由此可见,研究此类岩质陡立高边坡的稳定性对实际工程是非常重要的.
江颜[3]以露天铁矿岩质高边坡为研究对象,用极限平衡法和基于离散单元的强度折减法对边坡稳定性的进行定性和定量分析;周勇、王旭日等[4]针对强风化软硬互层岩质高边坡,对其锚杆应力、锚索内力、坡体位移进行了原位监测,并对该工程进行数值模拟分析,得出该边坡支护稳定,支护设计合理,为同类边坡支护设计提供相应建议;杜朋召等[5]为复杂岩质高边坡的稳定性分析提供了新的途径;乔兰等[6]通过与Mohr-Coulomb准则计算结果对比分析,得出CLFM模型在针对脆性硬岩高陡边坡中表现出良好的工程应用前景;夏栋舟等[7]结合FLAC3D动力分析原理,探究了在强震作用下岩质高边坡各个动力特性之间的关系;王乐华等[8]通过岩质高边坡发育的地质环境及变化特征,分析了高边坡存在的四种破坏模式,结合强度折减法对这四种破坏模式分别进行对比讨论.
基于强度折减法进行边坡稳定性分析时,可通过数值软件自动得出滑坡体的临界滑动面和安全系数,而且还可以模拟边坡失稳状态以及塑性区贯通情况.而极限平衡法则是根据极限平衡理论[9],建立力与力矩平衡方程,且需要事先给出潜在滑动面的位置.曾亚武、田伟明[10]经过边坡算例将强度折减法与极限平衡法的安全系数对比分析,结果表明两者差距很小,两个方法都可以进行边坡稳定性分析.
本文在阅读了大量的相关文献后发现,通过概化岩质高边坡的一般模型,选取坡高h、坡率i、开挖阶数n、不同结构面倾角β、不同结构面间距d、不同边坡坡脚α作为模型变量,系统开展坡体的变形破坏数值仿真工作.
1 基本原理与数值模型
1.1 强度折减法基本原理
强度折减法基本原理[11,12]就是将边坡的粘聚力c和内摩擦角φ均除以一个折减系数Fs,从而再重新得到一组新的c′、φ′值,再用折减后的参数进行计算,一直计算到边坡达到极限状态时,此时对应的折减系数Fs即为边坡的稳定安全系数:
c′=c/Fs
(1)
tanφ′=tanφ/Fs
(2)
强度折减法的优点就是软件可以通过弹塑性计算自动得出坡体的滑动面,同时得出相应的安全系数,并不需要事先假定,而且考虑了土体的本构关系以及岩体本身的变形.关于强度折减法对边坡稳定性失稳判据主要有三种:边坡某一特征部位是否发生突变位移、塑性应变区从坡脚到坡顶贯通、数值计算不收敛[13].对于三种判据的选用一直存在分歧,而裴利剑等[14]认为这三种判据理论上具有一致性.
1.2 数值模型
通过搜集大量相关工程实例,综合张鲁渝、郑颖人等[15]对边坡稳定安全系数的研究,建议模型左边界距坡顶2.5H,右边界距坡脚为1.5H,上下边界总高大于等于2倍坡高,模型左右边界施加位移约束,下部为全约束,上部为自由边界.本文采用平面应变模型,岩体与结构面均为实体单元、连续介质,赋予不同材料参数.先在CAD中画出二维模型,再导入ANSYS中完成模型的建立与网格划分的前处理,最后利用ANSYS-FLAC3D接口程序导入FLAC3D中完成计算.
计算均质几何模型如图1所示,建立如图2所示的均质计算模型,计算岩质高边坡的不同坡高h、边坡坡率i、边坡开挖级数n敏感性分析时使用计算的基本模型,均质边坡物理力学参数如表1所示.
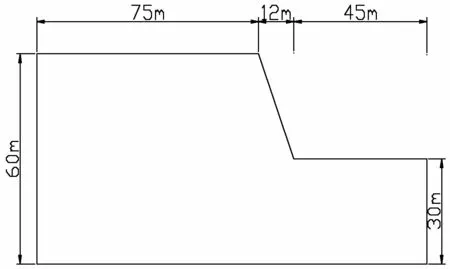
图1 计算均质几何模型
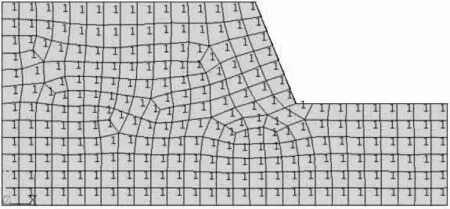
图2 均质计算模型

表1 均质高边坡物理力学参数
其中对边坡开挖分级影响因素进行分析时设计坡高为80 m,坡率1∶0.4,假设边坡的每级开挖高度相同,分别采取四级、五级开挖,开挖高度分别为20 m、16 m.四级开挖和五级开挖的计算几何模型分别如图3(a)、3(b).计算模型分别如图4(a)、4(b).
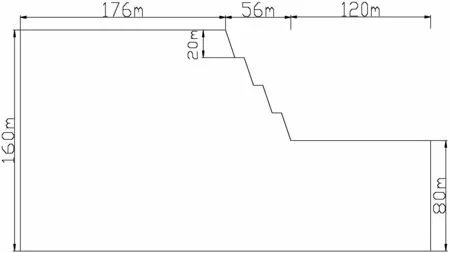
(a) 四级开挖计算几何模型
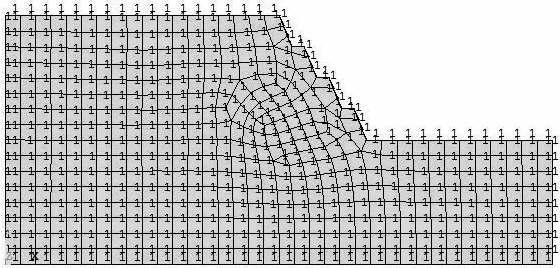
(a)四级开挖计算模型
进行不同结构面倾角β、结构面间距d、边坡坡脚α以及结构面粘聚力c和内摩擦角φ敏感性分析时,使用顺层、逆层结构面计算几何模型如图5(a)、5(b)所示.建立如图6(a)、6(b)所示的不同结构面岩质边坡计算模型.岩体物理力学参数如表2所示.
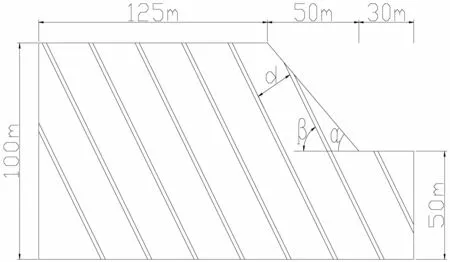
(a) 顺层结构面几何模型(0<β<90 °)
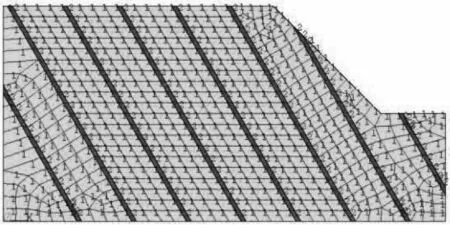
(a) 顺层软弱结构面计算模型
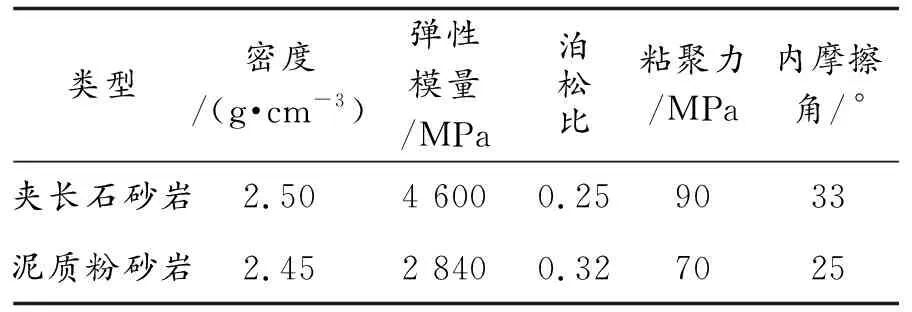
表2 岩体物理力学参数
1.3 屈服准则
本次计算依据Mohr-Coulomb剪切和拉伸屈服准则,可同时考虑岩质高边坡中岩体与结构面的力学属性.由于不同的材料特性,屈服可能发生在岩体内,可能发生在结构面上,或者两部分均发生.采用能同时考虑关联流动拉伸屈服和非关联流动剪切屈服准则的表达式[16]如下:
(1)剪切屈服准则:
(3)
(2)拉伸屈服准则:
ft=σ3-σt
(4)
式中:I1为应力张量第一不变量,J2为应力偏量第二不变量,θσ为应力罗德角,c、φ分别为粘聚力和内摩擦角;σ3为第三主应力,σt为单轴抗拉度.
2 坡高h、坡率i、开挖级数n对匀质岩性高边坡稳定性影响
2.1 坡高h影响分析
选取坡率i=1∶0.4,分别取坡高h为30 m、40 m、50 m、60 m、70 m、80 m 、90 m通过FLAC3D进行强度折减有限元分析得到危险滑动面,并计算出安全系数,不同坡高下的最大位移增量云图,如图7所示.
由图7可以得到:坡脚处的位移最大,滑动面都是一条光滑曲线,形状类似.坡脚处的位移增量尤为明显,因此在岩质高边坡的实际设计中,坡脚在边坡设计中是十分关键的位置.当边坡坡高越大时,对于坡脚的支护要求也就越高.比较各个坡高条件下的安全系数可知(如图8),在坡率一定的情况下,坡高h=30 m至40 m时的安全系数从4.8下降到3.695,下降速度较快,从坡高h=40 m时的安全系数为3.695下降至坡高h=90 m时的安全系数为2.102,下降速度较缓.总体可以看出岩质边坡的高度越大边坡安全系数有减小的趋势,稳定性越差.通过不同坡高对坡脚最大位移关系的比较(如图9)可以得到:当坡高h=30 m至70 m时坡脚最大位移增量从0.09 m增长到3.19 m,增长速度较快,而坡高h=70 m至90 m时,坡脚最大位移增量由3.19 m增长至3.41 m,增长速度较平缓.总体可以得到坡高增加,最大位移有增大的趋势.

(a)h=30 m
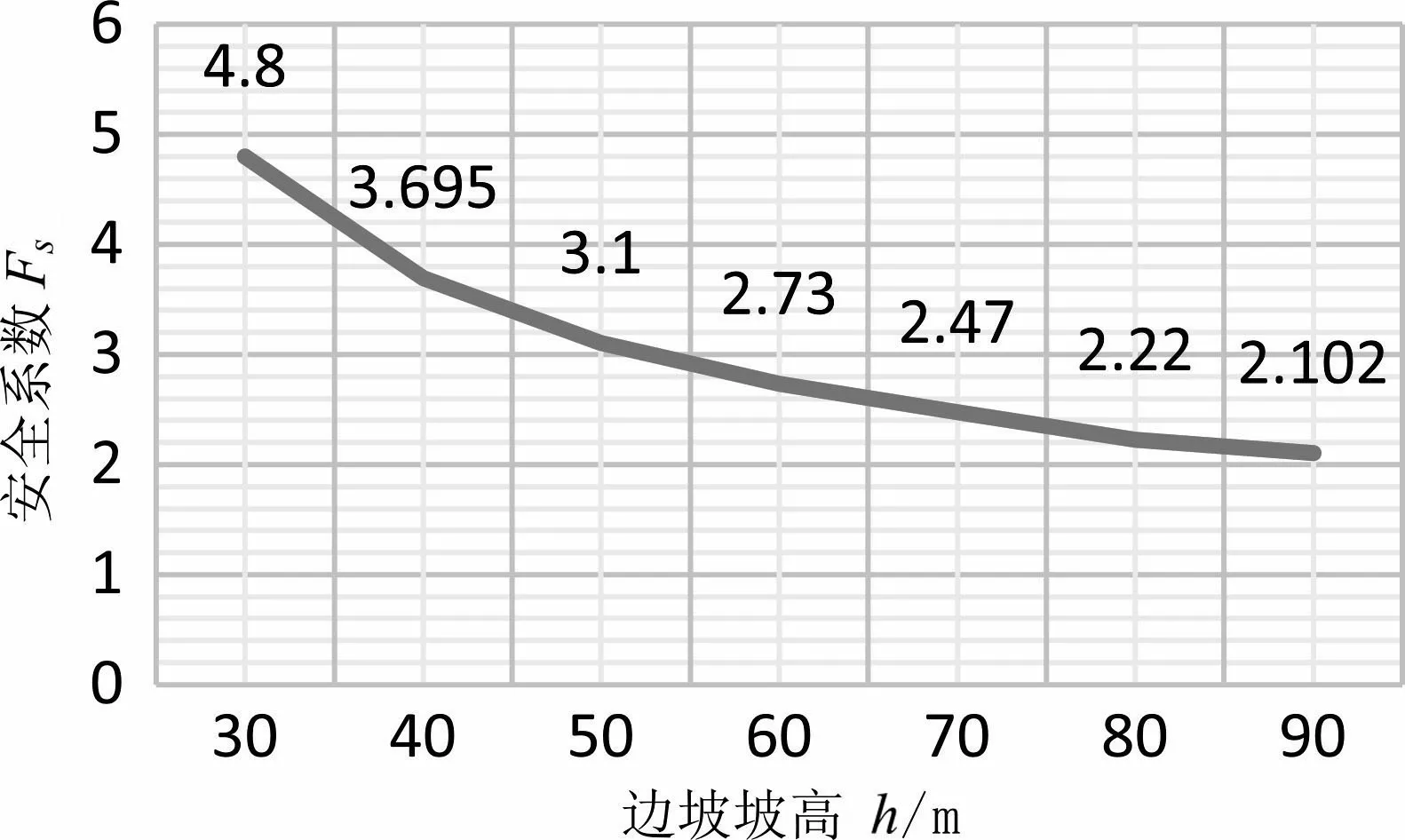
图8 坡高与安全系数的关系

图9 坡高与坡脚最大位移增量的关系
2.2 坡率i影响分析
坡率也是岩质高边坡设计中的重要因素,坡高h设计为60 m,选取坡率i为1∶0.5、1∶0.4、1∶0.25三种情况.通过FLAC3D进行强度折减法有限元分析,不同高度岩质高边坡最大位移增量云图如图10所示.由图可知:坡率的改变,对于岩质高边坡的最危险滑动面的形状影响不大,但是随着坡率越来越陡,边坡整体的位移增量在不断增大且位移增量最大位于坡脚处.比较各个坡率条件下的安全系数可知(如图11):当坡率i=1∶0.5时的安全系数为2.914,一直下降至坡率最大i=1∶0.25时的安全系数2.52,总体可以看出随着坡率越陡,安全系数也在不断减小,边坡的稳定性也不断减小,因此,在岩质边坡的设计中,需要在设计中寻找平衡点,即减小边坡的变形量,同时也不对边坡的稳定性造成太大影响.通过不同坡率对坡脚最大位移关系的比较(如图12)可以得到:坡率i=1∶0.5时坡脚的最大位移增量为1.49 m,坡率最大i=1∶0.25岩质边坡,坡脚的最大位移增量为2.57 m,说明了在岩体条件好的状况下,坡率越陡,边坡的变形越大.
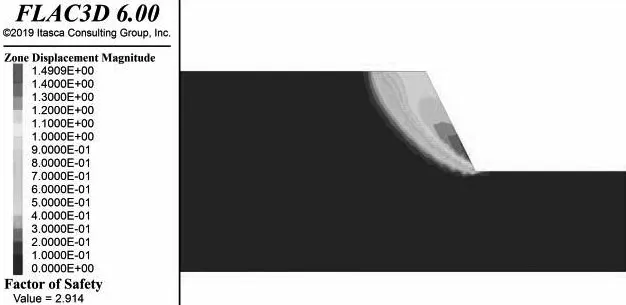
(a)i=1∶0.5
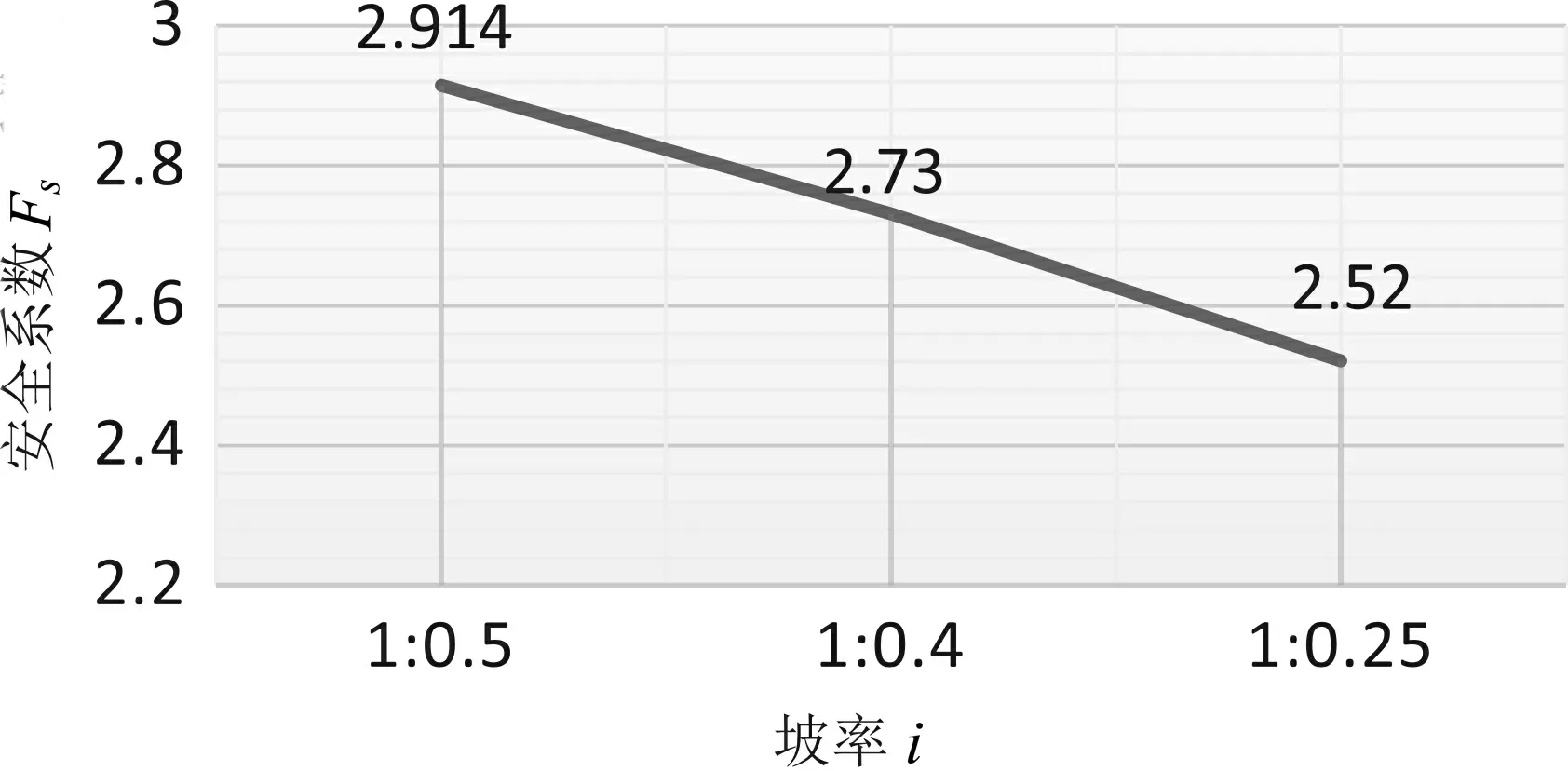
图11 坡率与安全系数的关系
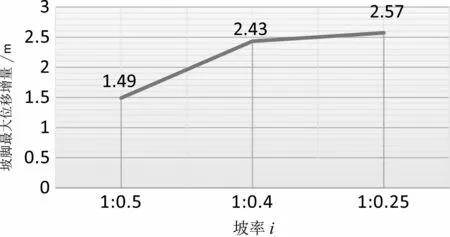
图12 坡率与坡脚最大位移增量的关系
2.3 开挖级数n影响分析
本文中设计坡高为80 m,坡率1∶0.4,假设边坡的每级开挖高度相同,分别采取四级、五级开挖,开挖高度分别为20 m、16 m,采用图5所示的计算模型模拟分析得到不同开挖级数的最大位移增量云图,如图13所示.

(a)n=5
通过比较不同的开挖级数岩质高边坡的安全系数(如图14),未开挖时的安全系数为2.22,增长至五级开挖时的安全系数3.695,可知分级开挖所得到的安全系数明显比未分级开挖的安全系数高,由此可以得到分级开挖能提高边坡的稳定性.但是在实际对边坡分级设计施工过程中,所消耗的施工花费以及支护花费会随着开挖级数的增加而增加,所消耗的施工时间也会增大,因此在实际的施工过程中,开挖的级数也要根据实际情况考虑,在安全系数提升不大的情况下,可以适当地减小开挖级数.在进行不同开挖级数最大位移增量的比较中(如图15),在未开挖时边坡的最大位移量为3.26 m,四级开挖时最大位移增量4.33 m,五级开挖时最大位移增量为5.54 m,分级开挖会产生更大的位移增量,因此在分级开挖的设计施工过程中,边坡的位移变形控制至关重要.
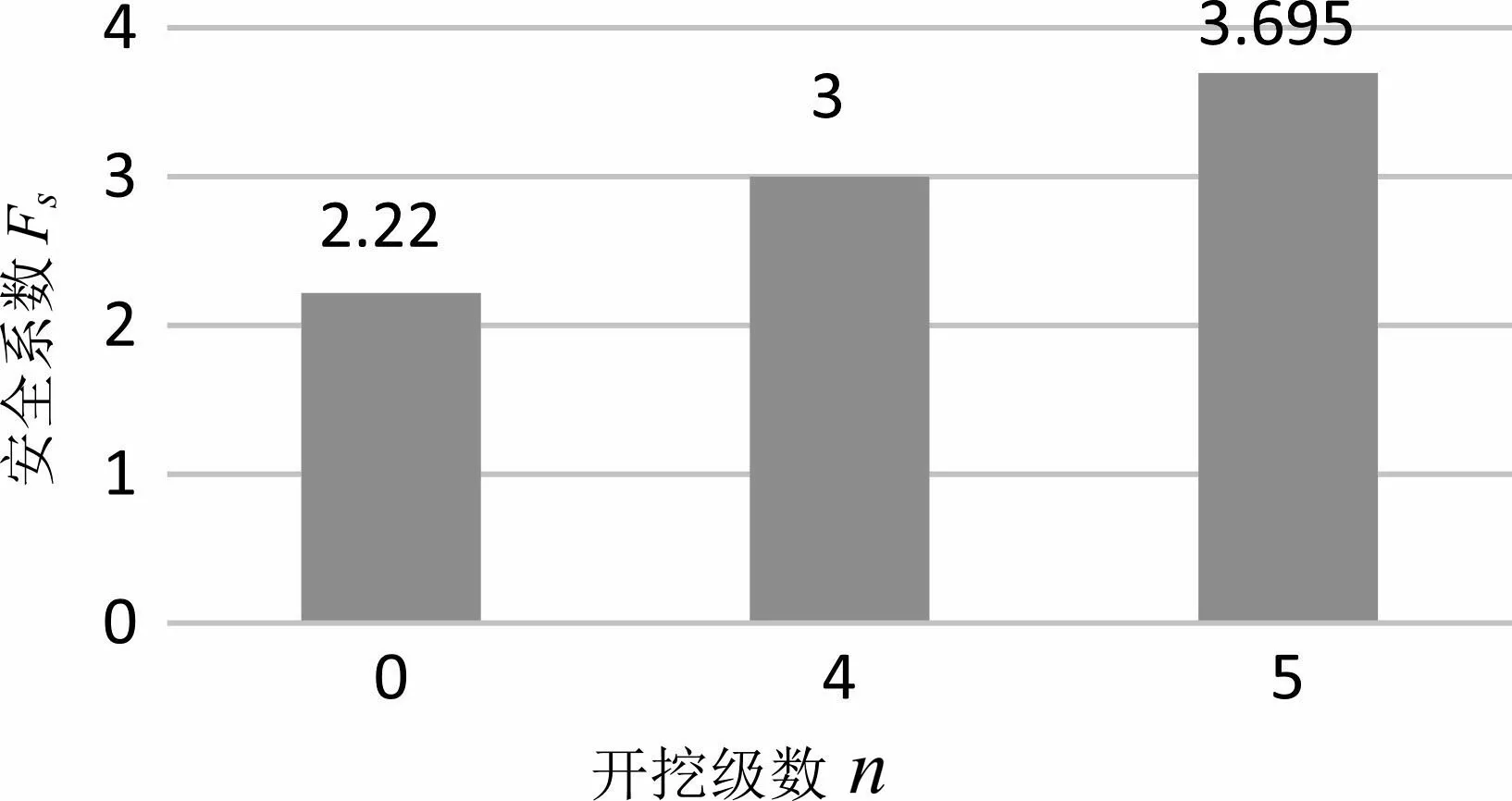
图14 开挖级数与安全系数的关系
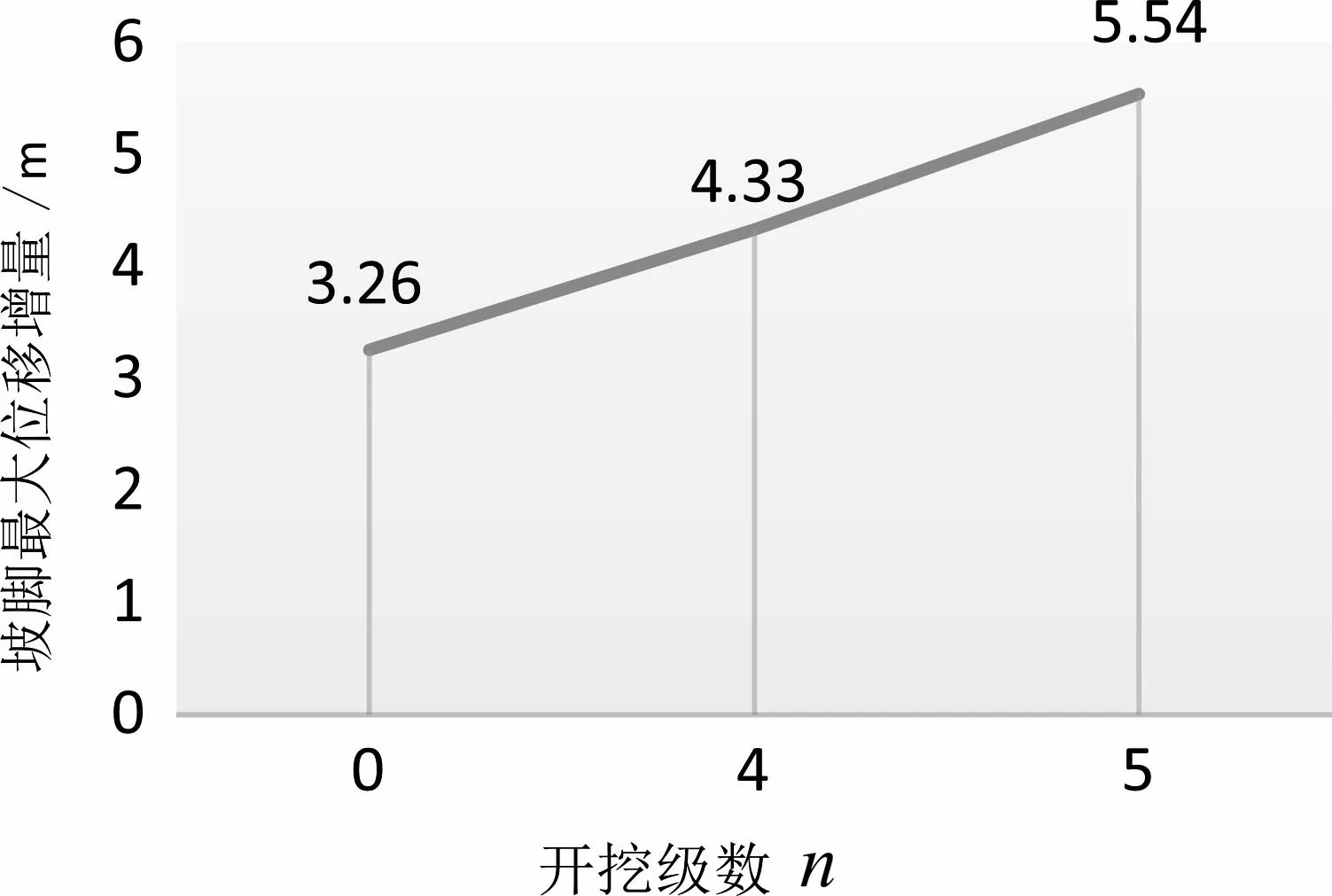
图15 开挖级数与坡脚最大位移增量之间的关系
在设计开挖级数的过程当中,开挖级数越多,每级的开挖高度也跟着降低,但是边坡的总体位移增量有增大的趋势,安全系数越大,稳定性越好.这说明在每级开挖高度不大的情况下,每级开挖高度增量不大的情况下,开挖级数对于位移的增量、边坡的安全系数的影响大于坡高对于边坡位移增量、安全系数的影响.
3 结构面对岩质高边坡稳定性的影响
3.1 结构面倾角β影响分析
在对岩质高边坡的稳定性分析中,岩体中存在的软弱结构面对边坡的稳定性影响尤为重要.软弱结构面会使岩体产生应力集中.如图5(a)所示,以边坡坡脚α=45 °,结构面间距为h=20 m,结构面倾角分别取不同的数值进行数值模拟.最大位移增量云图如图16所示.
经过对比不同的结构面对岩质高边坡的安全系数(如图17)可知:顺层岩质高边坡(0 °<β<90 °)的安全系数随着结构面的倾角先减小后增大,当结构面倾角为30 °时,安全系数最小为1.426,此时边坡的稳定性最差.由β=90 °的安全系数1.613大于β=0 °的安全系数1.5,可知直立层状岩质高边坡的稳定性要大于水平层状岩质高边坡,逆层岩质高边坡(90 °<β<180 °)的安全系数相较于顺层岩质高边坡更加平稳一些,稳定性要明显高于顺层岩质高边坡,其安全系数呈现出先减小后增大的趋势,当β=150 °时,安全系数最大为1.629,其稳定性也最高.
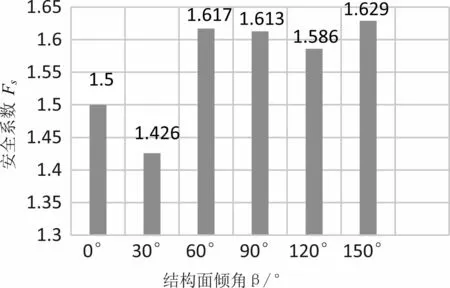
图17 结构面倾角与安全系数的关系
3.2 结构面间距d影响分析
以β=60 °,α=45 °保持不变,结构面间距分别选取d=20 m、d=25 m、d=30 m、d=35 m,分别对不同结构面间距的四种岩质高边坡对其破坏模式及稳定性进行数值模拟分析.由位移云图(如图18)可知:在不同结构面间距的条件下岩质高边坡的破坏模式基本相同,最危险的滑动面类似,滑坡体沿着软弱结构面下滑.不同结构面间距和安全系数的关系,如图19所示,结构面间距d=30 m时的安全系数1.617增长至d=25 m时的安全系数1.621,增长速度较缓,增长至d=35 m时的安全系数1.707,增长速度较快.整体可以看出安全系数会随着结构面间距d的增大而增大,边坡稳定性也会愈来愈强.

(a)d=20 m
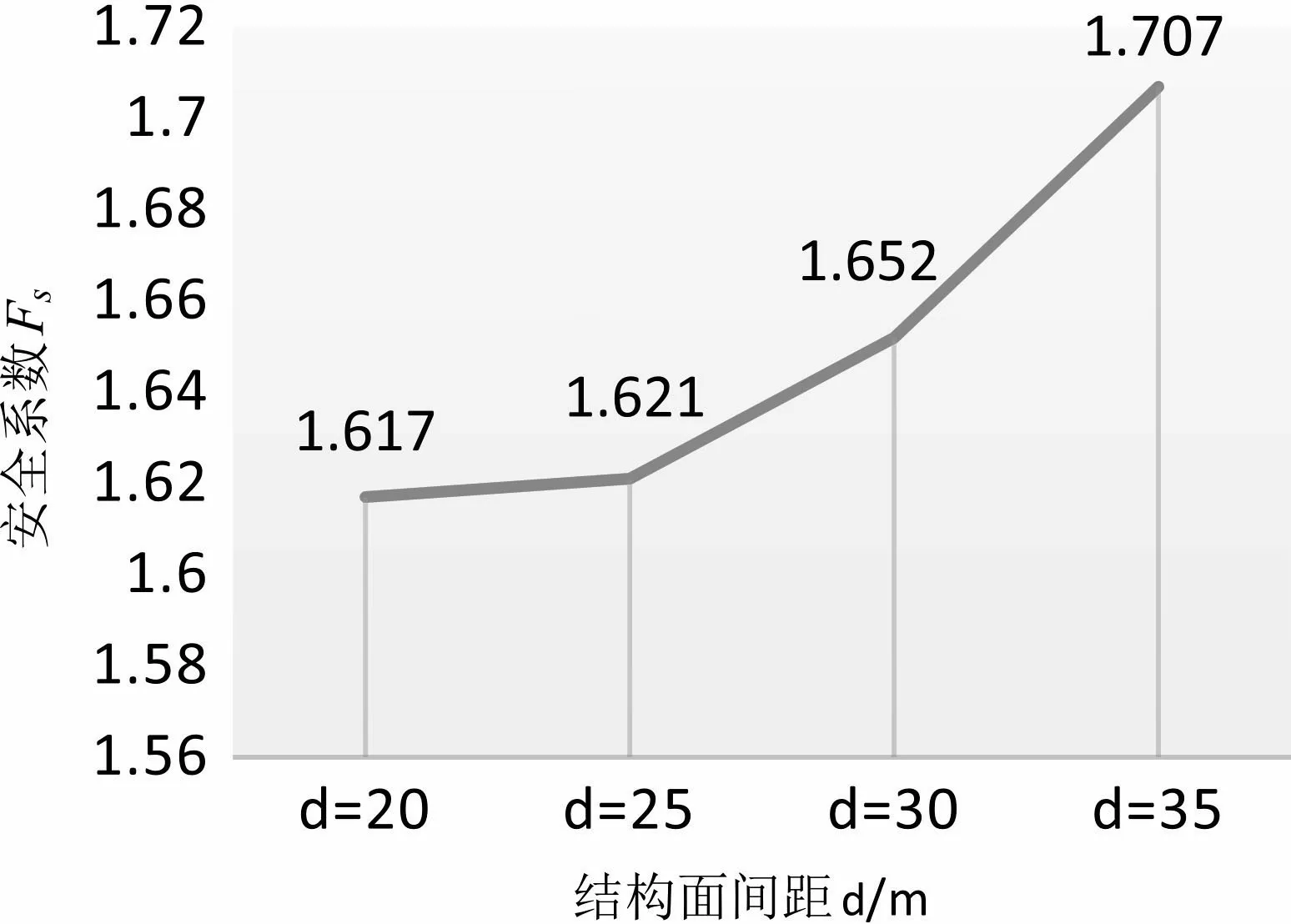
图19 结构面间距与安全系数的关系
3.3 边坡坡脚α影响分析
通过分析不同边坡坡脚α对岩质高边坡的影响,选取结构面间距d=20 m,结构面倾角β=60 °,分别选取边坡坡脚α为30 °、35 °、40 °、45 °、50 °.以图6(a)为基本计算模型,对岩质高边坡的稳定性进行数值模拟分析,所得到最大位移增量云图(图20)可知:滑动面形状随着边坡坡脚的增大会呈现更加陡立的趋势,从整体来看滑动面都是一条光滑的曲线.最大位移都集中在坡脚处,越接近坡面位移相对更大,并且是向坡面逐渐递增的趋势.由强度折减法计算出的边坡坡脚与安全系数的关系(如图21),由图可知,当坡脚增大,安全系数呈现降低的趋势,且下降趋势一致,当坡脚每增加5 °,安全系数平均降低0.11左右,由此可知边坡越陡立安全系数更低,稳定性越差,所以在边坡设计中,边坡坡脚是关键因素.

(a)α=30 °
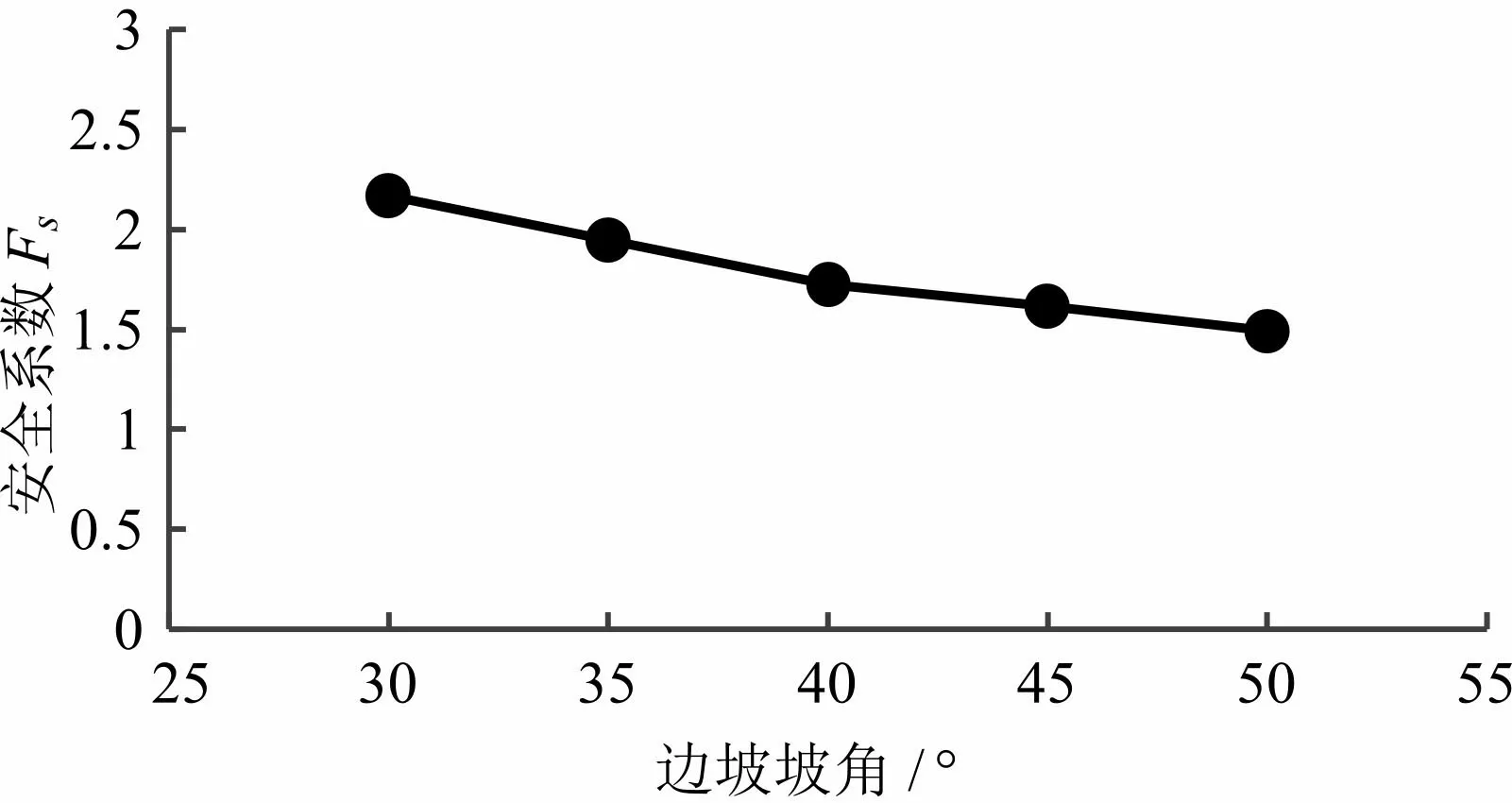
图21 边坡坡脚与安全系数的关系
3.4 结构面粘聚力c与内摩擦角φ影响分析
抗剪强度是影响岩质高边坡稳定性的重要因素,因此本文采取如图6(a)的顺层结构面计算模型来分析研究不同抗剪强度对岩质高边坡的稳定性影响,在表2的岩体物理力学参数基础上,采用控制变量法来分析研究。选取内摩擦角φ=35 °,粘聚力c分别取0.4、0.45、0.5、0.55、0.6五种情况进行分析研究(如图22),当选取粘聚力c=0.5,内摩擦角φ分别取25 °、30 °、35 °、40 °、45 °五组情况进行分析研究(如图23),由图22、23可以看出岩质高边坡的安全系数都会随着粘聚力c、内摩擦角φ的增大而呈现增大的趋势,稳定性更好。由此可得,仅仅改变不同的抗剪强度对岩质高边坡的稳定性变化都是类似的。
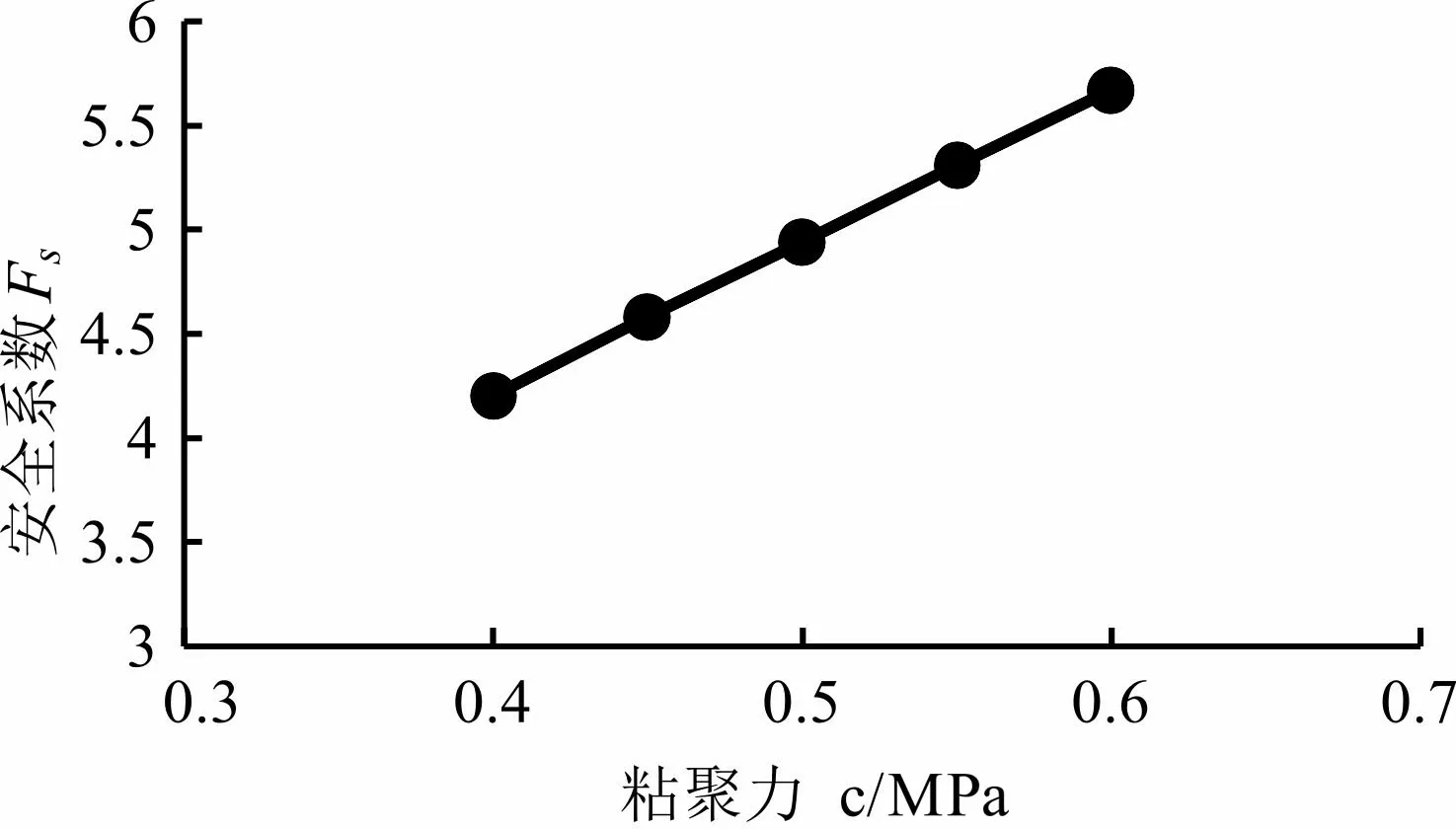
图22 粘聚力与安全系数的关系
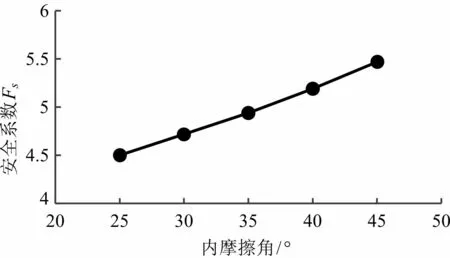
图23 内摩擦角与安全系数的关系
4 结论
(1)应用FLAC3D研究岩质高边坡时,当坡高h、坡率i、边坡坡脚α的增大,边坡安全系数减小,稳定性下降,边坡位移增量将变大,坡脚位置位移增量尤为显著;而当开挖级数n、结构面间距d、结构面粘聚力c、内摩擦角φ增大,边坡的安全系数将增大,边坡的稳定性越高,同时分级开挖的级数越多,边坡会发生更大的位移增量。
(2)软弱结构面对岩质高边坡的稳定性影响很大,顺层状边坡的安全系数随结构面倾角的增大呈现出先减小后增大的趋向且稳定性明显低于逆层状边坡。不同结构面间距情况下,边坡破坏的形式基本是相同的,但随结构面间距d的增大,相应的安全系数不断提高,边坡稳定性逐渐增强。
