我国省域建筑业高质量发展评价研究
2022-09-20王泽宇郑凯玥蒋俊杰张源江袁红平
王泽宇,郑凯玥,蒋俊杰,张源江,袁红平
(广州大学 管理学院,广东 广州 510006,E-mail:hpyuan@gzhu.edu.cn)
自“十二五” 以来,我国建筑业进入了转变发展方式和调整产业结构的深化改革阶段,正在逐步实现行业的工业化、绿色化与信息化转型,但目前仍然存在着“大而不强”“产能过剩”“资源消耗过大” 等突出问题,亟待由传统的“粗放型” 发展模式向新时代“精细化” 高质量发展模式转变[1]。
针对建筑业近年来面临的内部技术迭代升级和外部发展理念持续深化的复杂形势,学界不断探究能够表征其行业发展状态、引导其行业发展方向的评价体系。相关研究呈现出由单一关注发展规模和速度等量化指标向兼顾量与质的多维度、复合型指标体系的演化趋势。建筑业发展效率[2~4],可持续性[5,6]或创新能力[7,8]等凸显行业发展质量的关键要素逐步被纳入建筑业发展水平评价研究的指标体系范畴。然而这些研究多从单一视角开展测度,相关成果难以匹配高质量发展的新需求。尽管近年来陆续涌现出一些建筑业高质量发展评价研究[9~11],但目前关于建筑业高质量发展的内涵,评价指标构成和权重分配等问题仍需持续探索,更缺乏省域层面的实证研究来揭示我国建筑业高质量发展的区域化特点与差异。
本文在界定建筑业高质量发展内涵的基础上,综合运用文献分析法、三角模糊数改进层次分析法和模糊灰色物元模型,构建我国省域建筑业高质量发展水平的评价指标体系与评价模型,并通过2019年的省域面板数据,实证分析我国30 个省市地区建筑业高质量发展水平,为企业制定战略、政府把握建筑业发展水平和制定政策提供参考。
1 建筑业高质量发展评价指标体系
1.1 建筑业高质量发展指标体系的框架设计
对宏观经济发展而言,高质量发展意味着经济发展实现有效性、充分性、协调性、创新性、持续性、分享性和稳定性的综合,其突出强调的是具有生产要素投入低、资源配置效率高、资源环境成本低、经济社会效益好的质量型发展水平[12]。具体到我国建筑业,针对其目前所面临的“产能过剩”“效率不足”“耗能巨大”“转型滞后” 等突出问题,其高质量发展既要求实现产业规模、社会与经济效益和工程质量等发展效果的全面质量优化,更要求通过绿色创新深化实现行业发展过程的协调与效率提升[13](见图1)[14]。
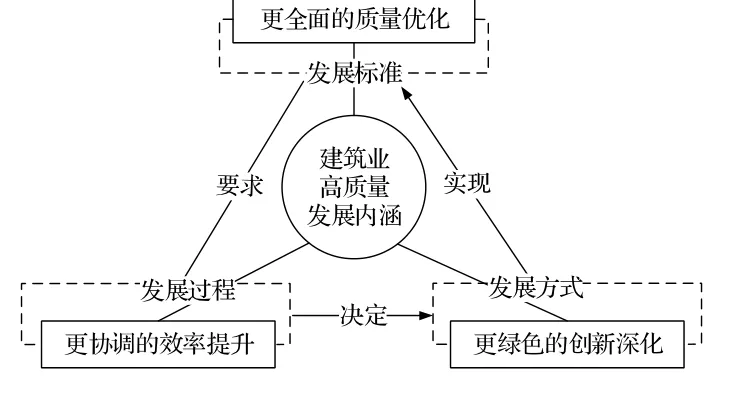
图1 建筑业高质量发展的内涵模型
根据建筑业高质量发展的内涵确立指标体系框架的设计思路,即构建能够凸显建筑业有效性、协调性、持续性、创新性等发展质量要素的多维度综合性指标体系。在此思路下,通过梳理包含建筑产业发展评价、建筑企业发展评价、建筑产品质量评价、宏观经济与产业高质量发展评价等与本文主题密切相关的文献资料42 篇,提炼出建筑业高质量发展评价的一、二级指标,形成了评价指标体系的基本框架,如图2 所示。

图2 评价指标体系基本框架图
1.2 建筑业高质量发展评价指标的筛选
结合专家访谈与可测度性分析,筛选能够表征二级指标状态的三级指标,具体筛选过程如下:
(1)一轮筛选。根据已构建的体系框架,结合科学性、全面性、可操作性、动态性、简明性的指标选取原则,从梳理的文献资料中提取用以表征17 个二级指标的三级指标共计42 个。
(2)二轮筛选。从政府、企业、科研机构等选取16 位行业专家就三级指标的全面性、代表性和可获得性进行访谈。根据专家反馈优化指标:一是科技进步贡献率涉及众多因素且存在不同的人为估算价值,我国近些年也未统计该指标数据,故删去;二是产品质量的二级指标修改为“质量” 和“安全” 两个维度,选用“单位产值生产安全事故数” 来衡量建筑业生产过程的安全性。
(3)最终指标的确定。本文数据来源包括国家与各省统计局发布的统计年鉴,CSMAR 和wind数据库,住建部、中国建筑业协会官方网站发布的发展报告和行业政策实施报告等。经调查发现,“建筑固体废物综合利用率”“建筑业专利数量” 和“SA8000 认证建筑企业占比” 不可获取。故而最终确定三级指标39 个,如表1 所示。

表1 我国建筑业高质量发展评价三级指标
1.3 三角模糊数改进层次分析法赋权
本文采用三角模糊数改进层次分析法计算各级指标的权重系数。该方法将模糊逻辑原理引入层次分析法中,通过对模糊不清的信息定量化来有效处理不稳定的问题。指标赋权步骤如下:
(1)构建三角模糊数判断矩阵。基于已构建的指标评价体系,运用层次分析法设计调研问卷,通过专家打分结果构建判断矩阵。调查问卷对象涵盖政府、企业和科研院所等机构专家,具体说明如表2 所示。共计发放问卷25 份,其中有效问卷19份,有效利用率为76%。专家按照层级依次将属于目标层的指标两两分析比较,并使用1~9 标度法明确其重要程度。根据专家打分结果,形成三角模糊数判断矩阵=。其中=(),且表示的是针对上一层同一个目标元素ai相比于元素aj的重要程度。为模糊数的下界,为模糊数的中值,为模糊数的上界。将t位专家所构造的三角模糊数判断矩阵综合为判断矩阵

表2 访谈专家资料背景
(2)一致性检验。计算判断矩阵的最大特征根λmax,引入一致性指标CI=(λmax-n)/(n-1),对判断矩阵进行一致性检验。本文中专家给出的判断矩阵均通过一致性检验。
(3)计算模糊权重。针对上一层级同一目标的n个同层指标元素,根据综合模糊判断矩阵,计算第i个指标元素的三角模糊权重ωi。
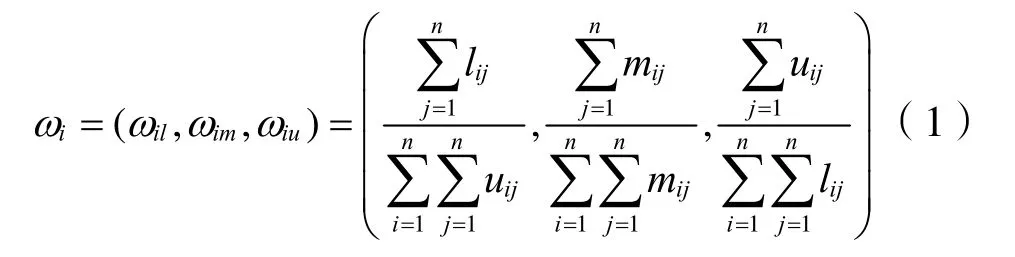
将各指标元素的三角模糊权重ωi进行两两比较,计算相应的可能度ρij。

式中,λ∈[0,1],λ值表示专家的风险态度。在本次实例计算中,采用风险中立的态度,取λ=0.5 代入计算。
(4)确定综合模糊权重。根据计算的可能度ρij构建模糊互补判断矩阵P=(ρij)n×n,将矩阵P进行合并归一化,得到最终的权重向量。
依照此步骤对已构建的三级评价指标体系进行了逐层级赋权,表3 给出了一、二级指标的综合模糊权重。由赋权结果可知专家判定绿色可持续性、行业创新能力与产品质量是体现我国省域建筑业高质量发展水平的关键因素。

表3 一级指标和二级指标的综合模糊权重
2 建筑业高质量发展评价模型
在已构建的指标体系的基础上,使用模糊灰色物元法建立建筑业高质量发展评价模型。该方法融合了可拓数学、模糊数学和灰色系统等多种理论,通过关联度分析定量、准确地表达出事物内部的矛盾问题,目前已应用于水质评价[15]、城市轨道交通项目建设风险评估[16]等领域。本文的评价指标体系维度众多、层次复杂,选用模糊灰色物元方法可以通过定量与定性结合的方式,将“评价区域对象”“评价指标”“评价灰量值” 作为基本要素,构建综合评价模型,对灰量值进行置换、分解、增减、扩缩等变换来实现物元的转换,解决指标之间不兼容问题。在定性和定量的基础上,通过灰色物元关联度分析,打破经典数学中的二值局限,消除评价过程中因指标体系之间的相互作用关系、定性评价的主观判断和数据采集时的数据失真等引发的“模糊性”。
2.1 构造复合模糊灰物元
给定事物的名称P,其特征值c的量值为v,这三者共同构成评价事物的评价物元R=(P,c,v)。如果事物P具有n个特征c1,c2,...,cn,与之对应的有n个量值v1,v2,...,vn,称R为n维模糊物元,简记R=(P,C,V)。如果m个事物的n维物元组合在一起,使构成m个事物n维复合物元Rmn。本文中各评价指标特征即为各项指标数据,与之相对应的模糊灰量值也是一个具体的数值,即灰色模糊白化值[16],用表示。若将Rmn的量值改写成模糊物元量值,则称为m个事物n维复合模糊物元,记作:

2.2 相对优化原则
由于评价指标众多且目前尚未全部具备明确的优劣界定标准,因此采用相对优化原则,即根据从优隶属度原则计算各评价指标与最优指标的相对隶属度,从而实现对选定评价区域间的比较和优劣排序。此外,本文获取的数据中存在着某些地区的数据与其他地区对应数据差距较大的问题,故采用经验法消除极值对隶属度计算的影响。即约有95%的数据在μ±2σ的范围之内,通过比较、与μ±2σ的大小,计算指标最优值,将其代入相对隶属度公式中,得出结果。其中正向指标相对隶属度公式为:

2.3 构建关联系数的模糊灰元
关联度是指两事物之间关联性的大小。本文采用关联系数来度量各评价方案与标准方案(各评价指标的取值为最优值)之间的关联程度,记作。因为关联系数和隶属度都是基于特定的取值,两者可以等价,即=,(i=1,2,…,m;j=1,2,…,n)。通过对式(3)中的m个评价地区n项指标的相对隶属度进行关联变换,可以得出各自对应的关联系数,并以此构造出m个评价地区n维的关联系数复合模糊灰元,记作。

2.4 计算关联度
关联度表示待评价事物和最优化标准之间关联性的大小,用Ki表示。通过关联度可以判段待评价事物的优劣程度。采用M(g+)算法计算第i个评价区域与最优化目标之间的关联度Ki:

根据计算结果,构造m个评价地区的关联度复合白化模糊灰元,记为。
3 实证分析
本文共统计得到2019 年我国30 个省市自治区(西藏、台湾、香港、澳门等地区因部分数据缺失未统计)在三级指标层面的原始数据。根据获取的原始数据,采用相对优化原则,通过式(4)、式(5)计算得到各指标的相对隶属度,取关联度等值于相对隶属度,通过关联度式(7)计算得出30个省8 个一级指标与最优化目标之间的关联度,并进行总关联度排序,总关联度越大,则地区的高质量发展状态越好,结果如表4 所示。
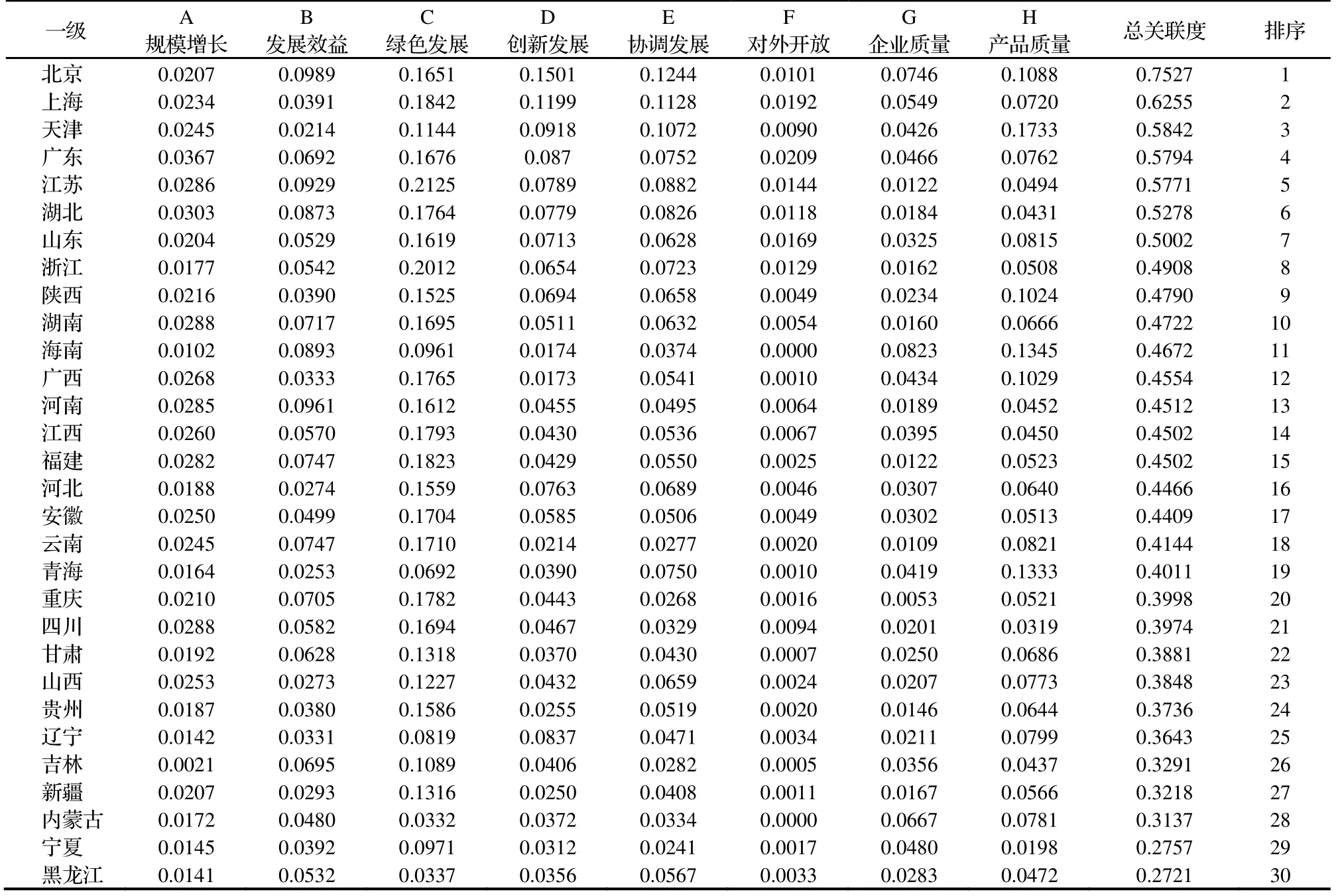
表4 我国省域建筑业发展评价指标关联度及排序结果
3.1 省间发展水平比较分析
本部分从地理空间分布特征、水平差异关键指标和发展特点相似性三方面比较分析省间建筑业高质量发展水平。
地理空间分布特征旨在识别各省市建筑业高质量发展水平的地理空间分布特点。根据各省市的地理位置分布可知我国省域建筑业高质量发展水平呈现出省间发展不均衡、东强西弱和部分地区集聚的空间分布特点。北京、上海、天津、广东、江苏处于全国领先地位,湖北、山东、浙江、陕西、湖南、海南、广西、河南、江西、福建处于中上游水平,河北、安徽、云南、青海、重庆、四川、甘肃、山西、贵州、辽宁处于中下游水平,而黑龙江、宁夏、内蒙古、新疆、吉林处于落后地位。“京津冀”“长三角”“珠三角” 等区域占据优势地位。
水平差异关键指标识别通过比较关联度系数的均值与标准差来识别引发省间高质量发展水平差异的关键指标。综合各一级指标关联度的平均值和标准差表现(见表5)可知绿色发展、产品质量与创新发展的关联度占比较高,且省域间存在较大差异,是引发省域间水平差异的关键因素。

表5 我国省域建筑业高质量发展关联度平均值与标准差
发展特点相似性分析旨在依照各省份建筑业高质量发展特点对其进行类别划分。本文利用K-means 算法,根据各省份8 个一级指标的相对隶属度表现对其进行聚类分析,具体分析结果如图3所示。根据聚类结果可知,我国部分省市间的建筑业高质量发展具有一定的相似性,并可分为4 种类别。其中,类别1 包括北京、天津、上海、广东,其在各一级指标上均处于领先地位;类别2 包括江苏、浙江、山东、河南、湖北、四川,其综合评价较好,但部分一级指标表现不足;类别3 包括河北、山西、辽宁、安徽等14 个省市,其综合评价不高,但部分一级指标表现较为突出;类别4 包括内蒙古、吉林、黑龙江、海南、青海、宁夏,其在质量和体量都表现不佳,在综合评价中处于落后地位。

图3 我国省域建筑业高质量发展聚类图
3.2 省间各维度均衡性分析
省间各维度均衡性分析旨在揭示各一级指标在不同省份间是否存在较大差异。本文采用计算一级指标在各省关联度的变异系数来衡量省间均衡性。由表6 的计算结果可知,各维度在省间的差异性较大,特别是对外开放、企业质量和创新发展,其关联度在30 个省市地区的变异系数分别高达0.9714,0.6000 和0.5385。说明我国建筑业因地理位置和经济发展的限制,导致部分省份对外开放受阻,企业质量难以提升,且创新能力差距明显。而规模增长、绿色发展与发展效益在省间的差异性则较小,其关联度的变异系数分别为0.3134,0.3151 和0.4025。说明随着我国资源环境约束的日益加剧和人们对美好生活的不断追求,各省份在重视建筑业规模增长的同时均注重行业的绿色与可持续发展。
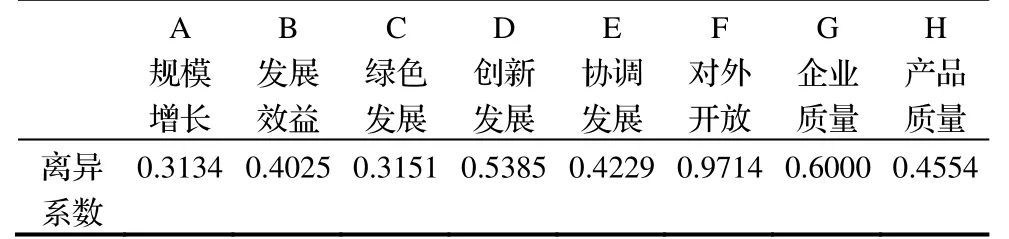
表6 我国省域建筑业高质量发展一级指标关联度变异系数
3.3 省内发展协调性分析
省内发展协调性分析旨在解析同一省域内各维度指标发展水平的协调性。通过对图3 进行横向比较,可见各省份不同维度间的发展呈现不均衡的态势。如北京、天津在创新发展、协调发展、产品质量领先于其他省份,但其在规模增长、绿色发展方面表现不足。说明北京、天津利用技术创新带动产业协调发展和提高产品质量,但目前建筑市场趋于饱和,发展规模和发展潜力处于劣势,且行业发展过程中资源消耗较高、绿色化程度较低。如江苏、湖北、湖南在规模增长、发展效益方面表现较好,但其在企业质量、产品质量落后于其他省份。说明这几个省份在关注发展规模的同时,注重行业发展对社会的贡献,但其对建筑工程品质的要求和标准不高,企业在生产方式、员工素质、经营可持续方面有待提升。
4 结语
精准评价行业高质量发展水平是推动建筑业转型升级的重要前提。本文在界定建筑业高质量发展内涵的基础上,构建了我国省域建筑业高质量发展评价体系,并实证分析我国30 个省市地区(西藏和港澳台除外)的建筑业高质量发展水平。研究发现,我国省域建筑业高质量发展水平不均衡,呈现东强西弱特点,“京津冀”“长三角”“珠三角”区域优势显著;省间各维度均衡性较弱。由于地理位置和经济发展水平的差异导致省间在各发展维度上的表现参差不齐;省内发展协调性不足。省内不同维度间发展水平均存在较大差异。
