异形PDC齿切削破岩提速机理研究

2022-09-20刘伟吉阳飞龙祝效华罗云旭

中国机械工程 2022年17期

刘伟吉阳飞龙祝效华罗云旭何灵

西南石油大学机电工程学院，成都，610500

0 引言

聚晶金刚石复合片(polycrystalline diamond compact，PDC)钻头自诞生以来，凭借其破岩效率高、设计灵活等优点而被广泛应用于石油与天然气钻采领域[1-4]，目前，世界范围内PDC钻头的进尺量已占到钻头破岩进尺总量的90%以上[5]。但是，随着钻井深度的增大，井底岩石高强度、高塑性及高研磨性等导致的钻齿易断裂、磨损等问题极为突出[6-8]。得益于整体材料科学和加工工艺的进步，近几年各种异形齿被广泛用于破岩钻头的设计上，如锥形齿、斧形齿、双曲面齿等，在特定地层都获得了较好的提速效果[9]。现阶段各种异形齿的破岩提速机理及差异还不清晰，研究异形齿的破岩机理对齿形选择及钻头布齿设计有重要意义。

钻井提速的根本问题就是破解岩石高效破碎的原理与方法，提高地层钻进速度，所以核心是钻头高效破岩技术和方法的问题。PDC单齿切削破岩是研究钻齿破岩机理的主要手段[10]，切削力是单齿破碎岩石实验中最常规、最能直接反映PDC齿与岩石之间相互作用的参数[11-16]，再以破岩比功为评价指标就可以对钻头破岩效率进行分析[17-22]。到目前为止，已有大量学者对单齿切削破岩机理开展了相关研究，主要针对不同钻齿切削深度、切削速度、倾角[18，20]等，这些研究主要针对常规平面齿。近年来石油钻井逐渐向深层迈进，井底岩石具有高强度、高塑性和研磨性等特性，且常规齿形的PDC钻头不适用于硬地层的钻进[23-25]，因而钻井提速面临巨大挑战。为提高钻头破岩效率，各种异形齿被广泛用于钻头设计上，其中大部分在实际钻井中取得了较好的提速效果。

研究发现，切削齿形不同，破岩效果不同，并且PDC齿的材料也会影响其在硬岩钻进时的性能[26-27]。通过有限元模拟计算及室内实验对不同形状PDC齿的切削力、破岩比功、切屑尺寸以及岩石断口微观形状等参数的对比分析发现：锥形PDC齿切削力比常规PDC齿小，且锥形PDC齿钻头的扭矩更小，钻井过程更稳定，但与常规16 mm PDC齿相比，锥形PDC齿的耐磨性能更弱[3，28]。三平面PDC齿更易压入地层形成破碎坑，预破碎区域更大，在钻进花岗岩地层时效果更好[29]。斧形PDC齿破碎非均质花岗岩时的切向力更小，更易破碎岩石[29]。脊形金刚石切削齿与常规的PDC钻头相比，在钻进过程中所需的破岩比功(mechanical specific energy，MSE)更低[30]。此外，具有浅凹特征的标准平面PDC齿不仅能减小破岩比功、提高机械钻速，还能降低钻齿上的切削热[31]。总体来说，异形齿比常规平面齿具有更好的破岩效果，但是现阶段的相关研究主要针对以上几种常见齿形，缺少对异形齿破岩的系统研究，其破岩提速机理还有待进一步揭示。

本文在单齿切削室内实验基础上基于有限元二次开发建立了异形齿切削破碎非均质花岗岩的三维数值仿真模型，系统研究了不同齿形切削破岩时的切向力、法向力以及破岩比功等。此外，还建立了全尺寸异形齿PDC钻头三维破岩数值仿真模型，研究了齿形对全尺寸钻头破岩效率的影响。本文的研究结果可为个性化钻头齿形选择及布齿设计等提供相应参考。

1 单齿切削破岩仿真模型

本文以河南驻马店花岗岩为实验岩样，该岩样为细粒花岗岩，晶粒尺寸约1 mm，主要包含的矿物组分及其质量分数分别为：石英12.2%，钠长石34.5%，绿泥石4.4%，斜长石41.1%，云母7.8%。花岗岩的基本力学特性如表1所示。

表1 花岗岩的基本力学特性Tab.1 Basic mechanical properties of granite

1.1 单齿切削破岩实验

1.1.1实验装置

单齿切削花岗岩实验在课题组自建的单齿切削破岩装置上进行，装置的切削部分如图1a所示。该装置可以精确控制切削深度，精度为0.01 mm，并且具有切削速度可调节的优点，能够较好地观测到岩石在钻齿切削作用下的破碎情况。数据采集系统的采样频率为10 Hz，切削齿为平面形PDC齿，前倾角为15°，直径为16 mm，钻齿倒角为0.3 mm。

本文所用岩样切削破碎后如图1b所示，岩性为灰白色花岗岩，其尺寸为180 mm×180 mm×130 mm。为确保实验过程中切削深度保持不变，岩石表面的平整度尤为重要，因此，在切削实验开始之前，先用平底PDC齿对岩石进行平端面处理。调节好切削深度后，再进行岩石切削实验，切削完成后对岩样进行收集。

(a)单齿切削破岩实验装置

(b)切削破碎后的花岗岩岩样图1 实验装置及岩样Fig.1 Experimental device and rock sample

1.1.2实验结果

在花岗岩单齿切削实验中，钻齿以固定切削深度1 mm和固定切削速度切削破碎岩石，得到的切向力变化规律和切削破碎的岩屑如图2所示，切削力平均值为1455.75 N，岩屑以粉末状为主，夹杂了一些块状岩屑。

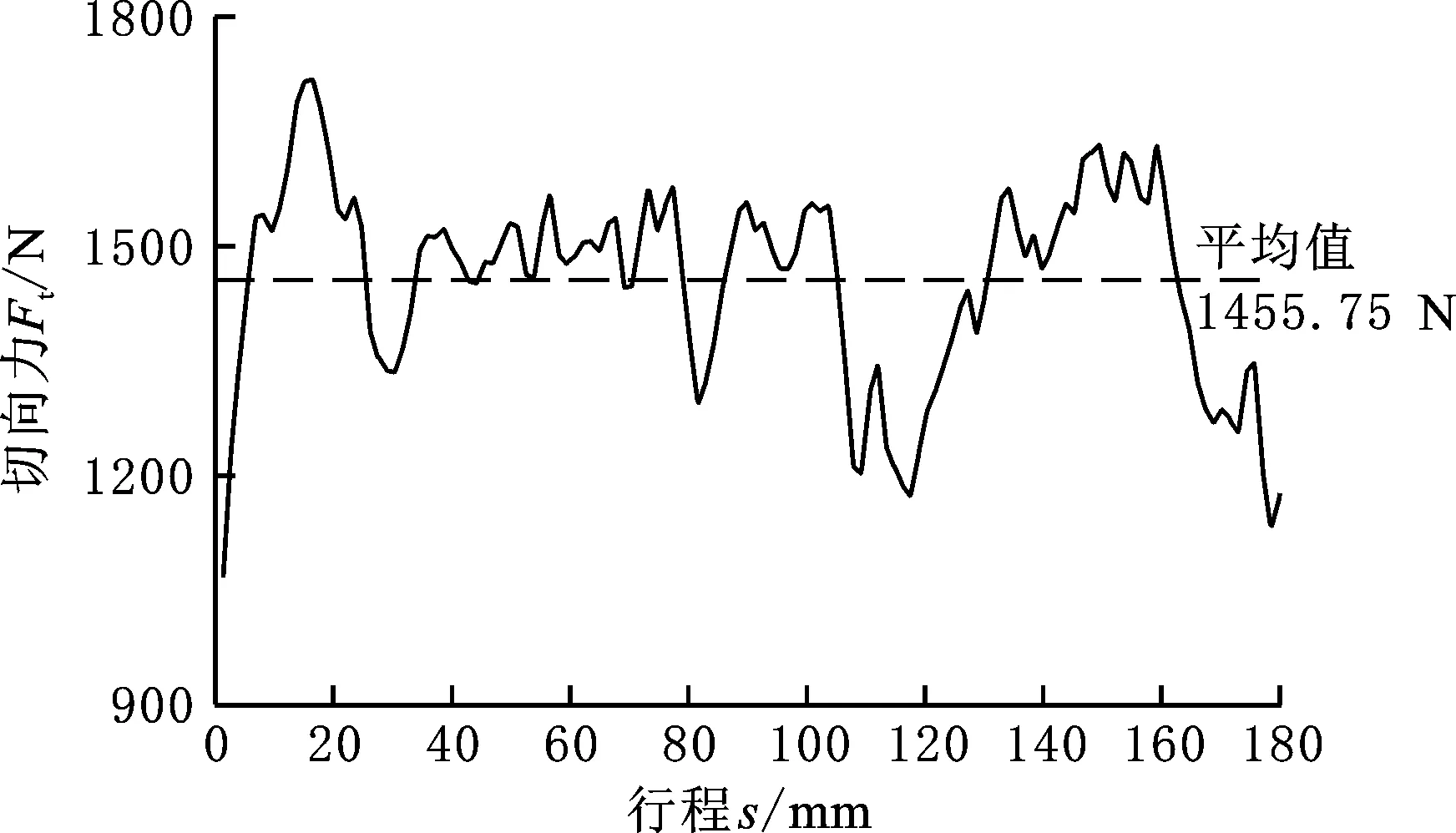
(a)PDC齿所受切向力

(b)破碎后的岩屑图2 单齿切削实验结果Fig.2 Single tooth cutting experimental results

1.2 数值仿真模型参数标定

基于有限元分析方法建立平面形PDC单齿切削非均质岩石的数值分析模型，如图3所示，并利用上述单齿切削实验对模型进行参数标定。切削模型的切削齿采用直径为16 mm的平面齿，并将其设置为刚体。切削齿的网格大小设置为0.7 mm，单元类型设置为C3D10M(修正的二次四面体单元)。岩石试样模型的尺寸为42 mm×25 mm×11 mm，为了更加真实地模拟花岗岩的细观非均质特性，对切削部分进行非均质建模，非均质部分的尺寸为26 mm×25 mm×5.5 mm。基于Voronoi算法，利用有限元二次开发建立了考虑花岗岩细观非均质性(几何非均质性、强度和变形非均质性)的花岗岩数值仿真模型。根据实验所得的花岗岩矿物组分含量，将生成的多边形赋予对应的材料属性，从而完成非均质部分数值模型的建立。

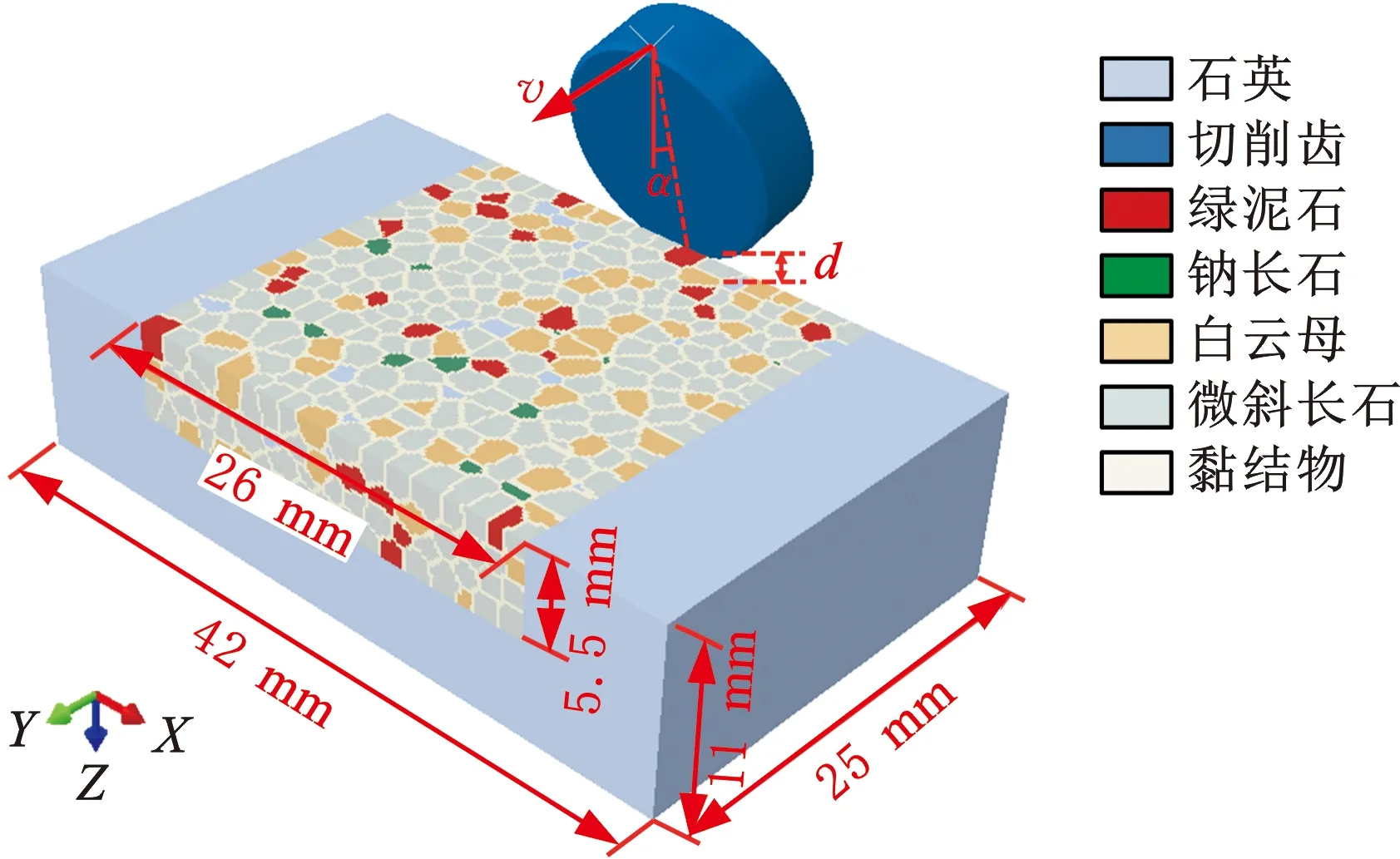
图3 平面形PDC单齿切削非均质岩石模型Fig.3 Planar PDC single-tooth cutting heterogeneous rock model

为了提高计算速度，只将非均质部分的网格进行细化，细化网格的尺寸为0.2 mm，其余部分进行适当粗化，粗化的网格尺寸为2 mm。岩石网格单元类型设置为C3D8R(八节点线性六面体单元)。相同材料之间选用具有各向同性损伤模型的Drucker-Prager本构模型，以研究其破坏模式，详细的标定方法在文献[32]中有详细介绍。不同材料之间用黏结物进行连接，用于模拟花岗岩晶粒间的连接状态。岩石其余部分的材料则赋予为石英属性。将岩石模型的底面和左右侧面的边界条件设置为完全固定，岩石的上表面和前后侧面(即垂直于切削方向的平面)为自由表面。切削齿的边界条件设置为：给定沿切削方向的切削速度v，并限制其余方向的速度和转速。岩石内部的接触设置为通用接触，切削齿与岩石之间的接触则设置为表面与表面接触。PDC齿以恒定的速度v=1 m/s切削岩石，切削深度与单齿切削实验中相同，为1.0 mm，PDC齿前倾角为15°。数值模拟计算的切向力如图4a所示，岩屑如图4b所示。

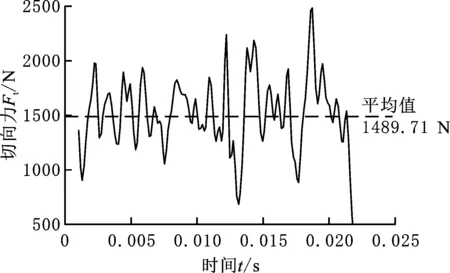
(a)PDC齿所受切向力

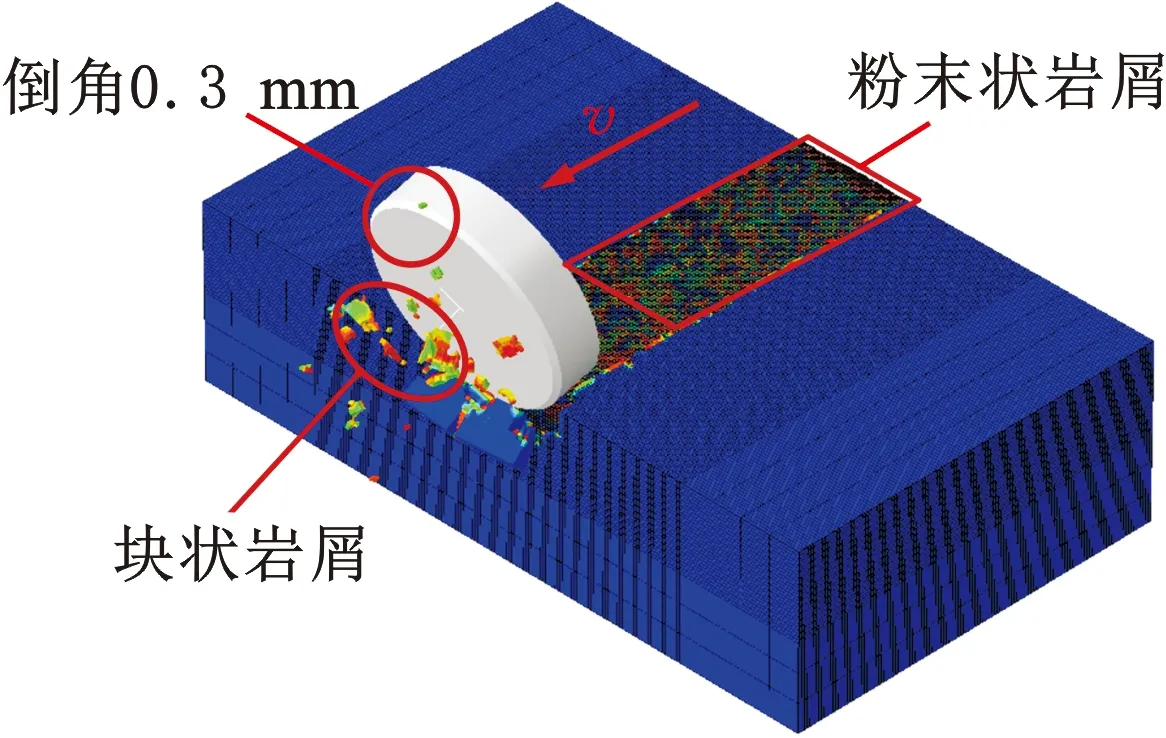
(b)破碎后的岩屑图4 单齿切削仿真模型计算结果Fig.4 Calculation results of single-tooth cutting simulation model

由图2a和图4a可得，单齿切削实验和仿真模型中的切向力平均值分别为1455.75 N、1489.71 N，误差为2.33%。二者误差在允许范围内，且切削破岩数值模拟也产生了相应的块状和粉末状岩屑，因此，数值仿真结果满足误差要求，即单齿切削数值仿真模型满足可靠性要求。

2 切削仿真结果分析

为了系统分析异形齿的切削破岩机理，本节建立了平面齿、凹面齿、凸面齿、奔驰齿、斧形齿、楔形齿、椭圆齿、鞍形齿、锥形齿、菱形齿、三平面齿及双曲面齿12种不同齿形的单齿切削非均质岩石模型，不同形状的PDC齿如图5所示，其中平面齿、斧形齿、锥形齿是工程中最常用的齿形。仿真模型中，除了PDC齿的形状不同外，其他切削参数均相同。

图5 不同形状的PDC齿Fig.5 PDC teeth of different shapes

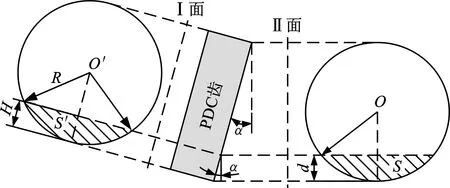
切削仿真结果如表2所示，其中，投影面积为图6中的面积S，将PDC齿向Ⅰ面投影得到PDC齿的正视图O′，向Ⅱ面投影得到PDC齿在垂直于切削方向上的投影图O。d为PDC齿的切削深度，切削前倾角为α，PDC齿在与岩石接触面上的投影面积为阴影面积S。R为PDC齿的半径，H为切深d在正视图上对应的高度，S′为阴影部分S投影在正视图上的面积。不同形状PDC齿数值模拟对应的切向力和法向力的平均值，以及不同形状PDC齿对应的破岩比功如表2所示。

表2 单齿切削仿真结果Tab.2 Single tooth cutting simulation results

(a)平面PDC齿

(b)锥形PDC齿图6 PDC单齿切削破碎花岗岩的投影面积示意图Fig.6 Schematic diagram of the projected area of PDC single-tooth cutting broken granite

由表2可知，12种异形PDC齿中，锥形齿的切向力最小，凸面齿和三平面齿上的切向力最大。结合图7的单齿破岩云图可知，锥形齿破碎岩石以塑性为主，锥形齿与岩石之间的作用力主要以摩擦力为主。相比于脆性破碎，塑性破碎少了切削力的“加载”和“释放”过程，力的变化过程更稳定。同时，由于少了“加载”过程，塑性破碎的切向力也会更小。锥形结构更易压入岩石，因此锥形齿上的法向力更小。由图7可知，奔驰齿的破岩方式也是以塑性破碎为主，但由于其齿面的脊形结构，PDC齿与岩石最先接触的面积相比于其他形状的齿更小，从而使得其切向力比同为塑性破碎的锥形齿更大。

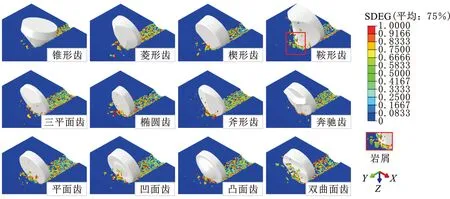
图7 不同齿形单齿破岩云图Fig.7 Different tooth shape single tooth broken rock cloud chart

平面齿、凹面齿和凸面齿的切向力比其他齿较大，但三者间差距较小。由图5可知，平面齿、凹面齿和凸面齿几何结构的不同点主要在于齿面的中心部分，齿面的边缘部分都相当于平面齿。当切削深度较小时，齿面与岩石接触面的形状都是平面，齿面结构对切向力的影响较小，此时不同结构的作用主要在于方便排出岩屑。

同时，由表2中的法向力可知，三平面齿和斧形齿与常规的平面齿相比，法向力均更大，即三平面齿与斧形齿上的尖脊形结构在压入岩石时所需的力更大。

如表2所示，由不同形状PDC齿对应的破岩比功可知，双曲面齿、鞍形齿和椭圆齿的破岩比功最小，锥形齿最大。但锥形齿切向力最小，结合图6可知，由于锥形齿投影在切削面上的面积最小，即破碎岩石的体积在所有齿形中最小，所以锥形齿的破岩比功反而最大。双曲面齿的齿缘有类似于犁形的结构，更易吃入岩石，破岩时的切向力更小。由表2和图7的破岩云图可知，双曲面齿内凹的齿面结构使破碎时更易产生体积较大的块状岩屑，破碎的岩石体积在所有齿形中最大，因此，双曲面齿的破岩比功最小。

相对于平面齿，由于三平面齿在破碎面上具有脊形结构，虽然更易吃入岩石，但切向力也比平面齿稍大。三平面齿比平面齿的切削力大1.24%，但是，三平面齿上尖脊的顶角比较大，使三平面齿比平面齿在破碎面上的投影面积小15.60%，因此三平面齿的破岩比功更大。斧形齿虽然也有类似的脊形结构，但由于它们的脊顶角比三平面齿的小，因此破碎面上的投影面积更小，更小的脊顶角导致齿与岩石的接触面积减小，使得齿上所受的切削力虽然更小，但其破岩比功却更大，所以斧形齿的破岩比功比三平面齿的大。奔驰齿则由于其脊顶角已经减小到锐角，脊形结构对岩石的劈剪作用更强烈，其破岩所需的切向力更小，因此奔驰齿的破岩比功比三平面齿和斧形齿的小。

综合切向力、法向力以及破岩比功分析双曲面齿、鞍形齿和椭圆齿可得，虽然双曲面齿的破岩比功在所有齿形中最小，但其切削力和法向力都比鞍形齿和椭圆齿大。鞍形齿和椭圆齿的破岩比功几乎相同，但鞍形齿上的切向力和法向力都比椭圆齿的小。同时，由图7可以看出，在切削过程中，鞍形齿产生的块状岩屑更多，尺寸更大，更易发生脆性破碎。因此综合分析，鞍形齿的破岩效果更好。

为了探究切削深度对切削破岩过程中的切向力和破岩比功的影响，建立了不同切削深度下的平面齿切削破碎岩石的数值模型。切削深度分别设置为0.2，0.4，0.6，0.8，1.0，1.2，1.4，1.6，1.8，2.0 mm。数值模拟实验结果如图8所示，不同切削深度的破岩云图见图9。

(a)切向力随切削深度变化趋势

(b)破岩比功随切削深度变化趋势图8 平面齿不同切削深度仿真结果Fig.8 Simulation results of different cutting depths of planar tooth

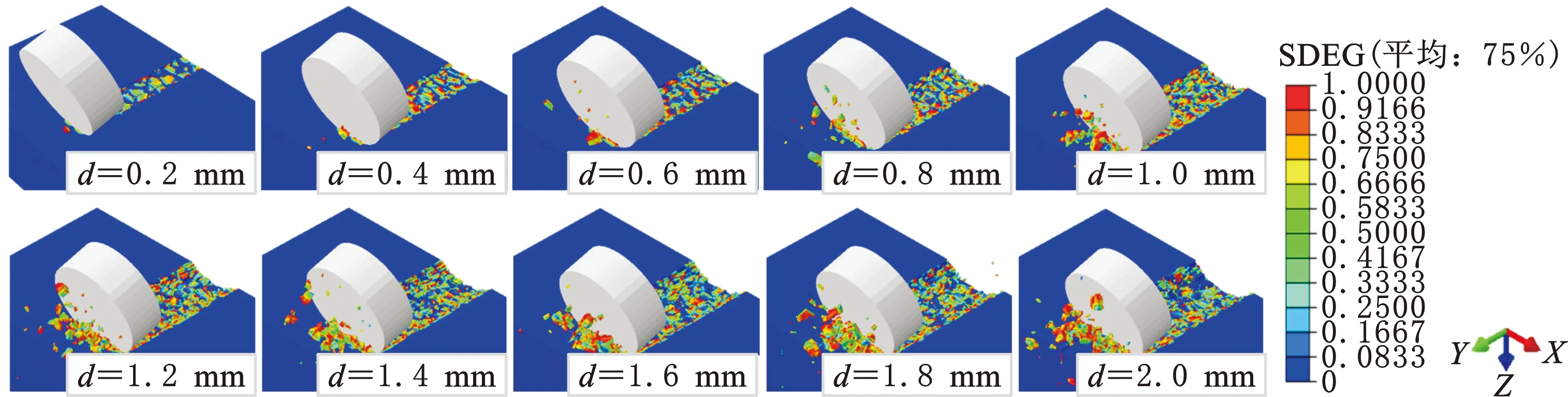
图9 不同切削深度单齿破岩云图Fig.9 Single-tooth broken rock cloud chart with different cutting depths

由图8a可知，切向力随切削深度的增大而增大，在本组模拟中，切向力随切削深度的增大几乎呈线性增大。但由实际的实验研究可知，切向力随切削深度的变化并不是线性关系，而是呈现双线性的关系。因实际的花岗岩岩石晶粒间会存在一些裂隙，而数值模型中的岩样为致密岩石，所以结果存在一些差异。同时，实验中的PDC齿存在一定尺寸的倒角，在切削深度较小时，切削齿与岩石之间的相互作用以摩擦为主，而不是数值模拟中的相互剪切，因此结果会存在一些差异。

由图8b可知，随着切削深度增大，破岩比功逐渐减小。且随着切削深度的增大，破岩比功的减小趋势趋于平缓。由图9可知，当切削深度较小时，破碎模式以塑性破碎为主，几乎没有产生尺寸较大的块状岩屑。当切削深度进一步增大时，块状岩屑的数量逐渐增多，岩石的破碎模式逐渐转变为以脆性破碎为主，也就对应了其破岩比功逐渐减小的趋势。

3 全尺寸异形齿钻头破岩结果分析

本节建立了全尺寸异形齿PDC钻头破碎岩石的数值仿真模型，模型中所用钻头的齿形分别为对应单齿切削模型中的平面齿、凹面齿、凸面齿、奔驰齿、斧形齿、楔形齿、椭圆齿、鞍形齿、锥形齿、菱形齿、三平面齿、双曲面齿12种不同齿形，模型中的钻头设置为刚体，全钻头模型以及各种齿形钻头的局部如图10所示。

图10 不同齿形的PDC钻头Fig.10 PDC bits with different tooth profiles

模型中的岩石试样为尺寸为φ500 mm×500 mm的圆柱体，PDC钻头上施加的钻压为5 t，钻速为9.41 rad/s，模拟钻进时间为10 s。每个模型中的PDC钻头除了齿形不同，其他参数均相同。不同齿形钻头的总进尺如图11所示，不同齿形钻头破岩的进尺及损伤云图见图12。

图11 不同齿形PDC钻头的总进尺Fig.11 Total footage of PDC bits with different tooth profiles

图12 全钻头破岩进尺图及云图Fig.12 Full-bit rock breaking footage and cloud chart

由图11可知，在所有不同齿形全钻头破岩仿真模型中，鞍形齿钻头的总进尺最大，双曲面钻头次之，锥形齿钻头的总进尺最小。结合表2、图7的单齿破岩结果可知，锥形齿的破岩比功最大，破岩效率最低，且锥形齿切削岩石以塑性破碎为主，因此锥形齿钻头的进尺仍然最小。由图5及图10可以看出，鞍形齿和双曲面齿在与岩石接触的边缘部分存在有类似于犁形的结构。与其他齿形的PDC钻头相比，具有犁形结构齿形的钻头更容易侵入岩石，总进尺更大。鞍形齿作为结合斧形齿和曲面齿特点而设计的一种新齿形，与岩石的相互作用以及破岩方式既有斧形齿的特点，也有曲面齿的特点。鞍形齿以齿缘犁形结构和中部脊形结构的集中力侵入岩石，能在一定程度上对齿前方和两侧的岩石造成预破碎，使岩石产生裂纹并释放掉岩石的内应力，从而使鞍形齿前端和两侧的岩石更易破碎，因此使得鞍形齿钻头的钻进速度更快。

双曲面齿相对于其他形状的齿，因为齿缘具有犁形结构的原因，破岩效果更好，钻进速度更快。但相对于鞍形齿，双曲面齿缺少齿面中部的脊形结构，齿两侧岩石的破碎效率要低一些，因此，双曲面齿钻头的进尺大于其他齿形的钻头但小于鞍形齿钻头。

其他齿形的全钻头计算结果中，斧形齿钻头因具有脊形结构，所以比其他几种钻头的进尺大，其余几种钻头的进尺情况则比较接近。值得注意的是，凹面齿钻头和凸面齿钻头进尺的差距较大。但由表2的单齿切削结果可知，凹面齿和凸面齿破岩的切向力、法向力以及破岩比功都十分接近。造成这种差距的原因可能与齿面结构有关，如图5和图7所示，凹面齿上的凹槽在切削深度或切削前倾角较大时，相当于一个犁形结构，相比于平面齿更易破碎岩石。而凸面齿上的圆弧顶结构，可能会对切削齿前方还未破碎的岩石造成挤压，从而使岩石更难于破碎。在单齿切削切削实验中，切削深度固定不变且没有考虑钻齿前倾角的影响，因此两种齿的破岩情况接近。在全钻头破岩中，钻齿的切削深度以及钻齿相对于岩石的前倾角是处于变化状态的，当切削深度较大时凹面齿的结构还类似于双曲面齿上的犁形结构，亦能提高破岩效率，因此会出现凹面齿钻头进尺大于凸面齿钻头的情形。