借线段图之东风 扬学生几何直观素养之帆

林娟彬

（连江县琯头中心小学，福建 连江 350500）

几何直观主要是指运用图表描述和分析问题，变抽象为形象，从而有利于打开学生解决问题的思路的能力［1］。几何直观把复杂的、难以理解的文字通过图形表达出来，让思维可视化。由于小学生几何直观方面的相关意识较弱，教师在教学中也难以对学生进行有效引导，常常会出现教师讲得大汗淋漓，学生却听得云里雾里，课后遇到同一类题又在纠结中的情况。这一方面是由于学生自身身心发展受限所导致的空间想象能力薄弱；另一方面也存在部分教师对于学生几何直观素养的培养不够重视，没有将其作为讲授重点系统化阐述，因此学生在一知半解之下未能灵活应用该方法来解决复杂问题。

一、借线段图培养几何直观素养的意义

小学生第二学段主要以具象思维为主，逐渐过渡到第三学段的抽象思维。在低年级解决问题的教学中，仅仅通过阅读题目中的文字叙述是很难找出数量关系的。而线段图作为小学数学教学中经常运用的几何直观表现形式，就成为了解决这一难点的指路明灯。几何直观可以通过线段图的形象关系直接感知复杂问题中的数量密码，有利于学生快速理解题意、梳理数量关系、构建数量模型，从而提高解决问题的效率和准确率。借助线段图的几何直观教学要从低年级开始孕伏，让学生在潜移默化中养成自觉应用线段图解决问题的习惯，这对提高学生分析和解决问题的能力以及丰富学生的数学思维层次大有裨益［2］。

二、用线段图培养几何直观素养的策略

（一）寻找数量关系，巧用线段图解难题

1.线段图悄播感知之种。研究表明，小学生的思维认知水平较为简单，其中直观思维的发展程度高于抽象思维，因此教师应尽可能地培养学生的几何直观能力，使得学生对所掌握的知识不仅仅停留在浅层，而是更透彻地了解知识的本源，灵活应用于解决数学问题［3］。其中，线段图在应用题的解析中承担了不可或缺的角色——它的几何直观作用，在抽象数学问题与具体几何图形之间架设桥梁，化繁为简。教师在教学过程中要注重引导学生尝试用线段图分析重组题中的数学信息，使其构建出更加直观形象的数量关系模型，达到简化题目中的条件与设问目的的同时，悄然在学生心中用线段图浇筑出几何直观的感知基石。

2.线段图速析数量关系。要打破学生见复杂应用题色变的困境，关键在于提升学生的数学核心素养，而画线段图便是一种行之有效的方法，它使得抽象复杂的难题在学生眼里不过如同纸老虎。以“差倍问题、和倍问题”的解决问题教学为例：小南妈妈今年的年龄是小南的4 倍，两者相差27 岁，小南多少岁？此题用倍、差两种方式来表示二者的年龄数量关系，理解起来较为抽象，而应用线段图则显得通俗易懂。

学生初识线段图，由于缺乏画图的经历，难以在脑海中形成清晰的解题路径。因此，教师在教学中要指引学生“认识—理解—强化”画图方法，使其快速掌握并灵活应用。解析数量关系的要点在于：①准确筛选条件信息；②明晰转化数量思路；③合理绘制线段图。对于上述问题，教师可以启发学生尝试将两个量的关系读“厚”：把两个数量关系切割成几个小问题以帮助学生梳理其中的联系，具体如图1 所示：（1）把哪个量看成一份？如何在图中表示？（2）把小南的年龄算作一份，那妈妈的年龄相当于这样的几份？又如何在图中展示？（3）图中哪一部分表示妈妈比小南大27 岁？

图1 小南和妈妈的年龄数量关系示意图

学生掌握了解析数量关系的步骤与技巧，不但不再惧怕复杂的数学问题，而且在画线段图过程中渗透了变换思维、数形结合思维、符号思维，促进对几何直观的理解。

（二）构建数量模型，提升几何直观之感

几何直观可以构建问题的直观模型，利用图来分析实际情境与数学问题，开辟解决问题的新路径。线段图能活化学生的活跃思维，成为学生自主探究意识的培养的催化剂［4］。数量关系都带有一定的抽象性，让学生通过线段图构建数量模型，对几何直观进行深入感知，是几何直观能力培养的重点。例如（见图2）：裤子的单价是50 元，上衣的单价是裤子的3 倍，购买一套这样的衣服需花费多少钱？大部分的学生会有这样的思维定式：一条裤子的单价+一件上衣的单价=一套衣服的总价。教师不急于纠正，当呈现出线段图后，让学生对其进行感知，他们便会有“柳暗花明又一村”之感：一套衣服的总价就相当于一条裤子的（3+1）倍。原来线段图是会说话的，其简洁性与概括性不仅让学生解题更加如鱼得水，而且感受到解决问题策略的多样性。

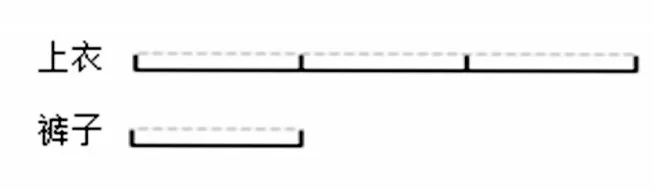
图2 上衣与裤子的价格数量关系示意图

紧接着教师出示这样2 道题目：

①因为暴雨，通往景区的路坏了，两个工程队同时进行抢修。他们分别从两端相向施工，道路长675m，2.5 天就修完了，甲队每天修筑126m，乙队每天修筑多少米？

②如图3 所示，4500 元可以购买几套这样的办公桌椅呢？你能把这张发票填写完整吗？

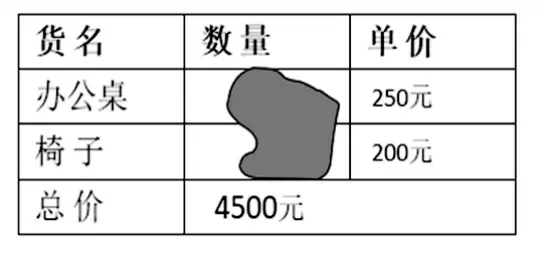
图3 办公桌椅的价格数量关系示意图

当学生尝试解答这2 道问题以后发现都可以用前面例题中学习的线段图建立数量模型ax+bx=（a+b）x。

学生养成做题时的画图构建模型的习惯后，在日后的学习中自然就会学会从不同角度去分析、思考和解决问题，进一步体会几何直观的奥妙之处。

（三）及时复盘反思，渗透几何直观思想

解决问题不是单纯的列式计算，而是要学会梳理问题，建立模型，练就触类旁通的能力，让几何直观的思想走得更远。有了激发体验之后，要让学生学会进行回顾反思，这可通过多次设问来引导，如，列式是否正确？能用其他方法得出相同结论吗？用同样的方法还可以解决什么样的问题呢？在教学中，让线段图成为学生在回顾反思环节的重要工具。

以图4 为例，让学生围绕上述所提问题进行讨论后得出：生1：可以通过路程、时间、速度之间的数量关系来找出题中的等量关系。生2：画线段图，可以非常直观看出两个一小时的路程之和，这样很容易找出等量关系。生3：可以借助这个等量关系检查自己的做法对不对。

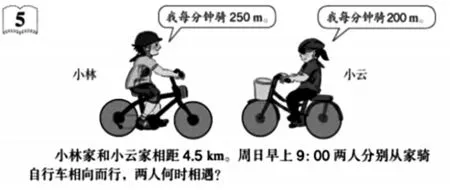
图4 五年级下册解决问题教学情景图

这样，既避免了学生只是注重解题结果正确与否，更重要的是借助线段图直观地理解数学世界的丰富多彩，逐渐将几何直观内化于心。

通过几何直观探索解决问题的思路，学生从自然应用线段图解决问题慢慢到用线段图解决其他的问题，不仅使抽象难懂的知识形象化，同时形成了相应的思维过渡，提升了数学思维。