基于DDAE的交流接触器状态特征融合方法*
2022-09-20高士珍刘树鑫
高士珍, 刘树鑫
(沈阳工业大学 电器新技术与应用研究所, 辽宁 沈阳 110870)
0 引 言
交流接触器是一种主要对交流回路和控制电路进行远距离频繁通断操作的低压控制电器[1],其工作状态对整个电网的安全运行有着关键的作用。对其进行状态评估和剩余寿命预测一直是低压控制电器方向的研究热点。
采用数据驱动的方法进行交流接触器剩余寿命预测研究不需要对其进行精确的物理模型构建,因此被广泛应用,但是该方法的前提是最大程度地获取能够反映交流接触器运行状态的特征参数。文献[2]提出变权重系数的方法,结合模糊综合评判方法,对交流接触器进行状态评估。文献[3]采用音频特征预测交流接触器电寿命,用卷积神经网络建立预测模型。文献[4]在交流接触器寿命预测中使用MIV确定模型,其输入为累积燃弧能量、吸合时间,分析了不同模型的预测误差。文献[5]利用触头质量损耗建立时间尺度变换模型并建立非线性Wiener预测模型,均取得了较好的研究成果。但是这些方法采用的特征量较为单一,缺少对交流接触器运行状态特征参数的充分提取。由于交流接触器的电寿命远远低于其机械寿命,所以先前的研究往往只考虑其电参量的相关特征,忽略了其机械参量的相关特征,这种研究手段过于简化。通过采集交流接触器运行过程中的振动信号[6],从中提取出与其状态相关的机械特征参数,对仅考虑电参量的研究方法进行特征补充,能够较为全面地反映交流接触器的运行状态,对其状态评估和寿命预测具有重要意义。
仅从是否能够充分反映交流接触器运行状态的角度来看,提取的特征越多,表征能力越强,但是考虑到目前采用数据驱动的研究方法,多采用机器学习和深度学习模型,其输入量的维度越大,训练难度和计算量是成指数上升的,因此如何以较少的特征在最大程度上反映交流接触器的运行状态是问题的关键。
针对上述问题,本文提出一种基于深度降噪自动编码器(Deep Denoising Autoencoder,DDAE)的交流接触器运行状态特征融合方法,从交流接触器全寿命试验运行数据中,提取电参量相关的和机械参量相关的特征参数,建立DDAE特征融合模型,在最大程度保留原始特征信息的基础上,进行特征融合重构,最后通过实验数据进行分析验证。
1 研究方法
1.1 基本自动编码器
自动编码器[7]是一种可以进行非监督学习的神经网络模型[8],可以学习到输入数据的降维表示,能够作为功能性非常强的特征检测器,因此可以作为机器学习和深度学习模型的预训练模型,实现深度神经网络模型输入的降维处理,进行特征融合重构。


图1 无监督学习原理
一个简单的自动编码器模型可分为编码器和解码器两个部分。自动编码器网络结构如图2所示。

图2 自动编码器网络结构

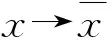
f(x)为编码函数,g(x)为解码函数,自动编码器的基本形式为
(1)
训练过程的约束为

(2)
即设计一个损失函数,让编码器的输入和输出尽可能相似,即

(3)
1.2 降噪自动编码器
基本自动编码器仅学习了上述的恒等函数,可能导致过拟合现象。和基本自动编码器不同,降噪自动编码器(Denoising Autoencoder,DAE)在训练过程中对原始的数据加入了干扰噪声,进行部分“破坏”处理,普遍认为,对完整原始数据编码得到的中间层能够重新恢复原始数据并不能证明这个网络就是优秀的;而能从在一定程度上被“破坏”的输入数据进行编码、解码运算后,还能还原完整的未被“破坏”的原始输入数据,这样得到的中间层特征才是优秀的,可以最大程度地保留原始特征的信息[9-10]。DAE网络结构如图3所示。

图3 DAE网络结构

DAE的编码过程为
(4)
DAE的解码过程为
z=g(h)=wdh+bd
(5)
损失函数为

(6)
式中:h——输出层激励函数;
f——输入层激励函数;
b——偏置项;
w——权重值;
z——解码后还原特征;
g——输出层激励函数;
L——损失函数。
通过以上计算,最终根据L值最小确定最佳网络结构。
1.3 DDAE
DDAE是对DAE的改进,普通DAE的中间层只有一层,而DDAE神经网络的中间层可以有多个,可以理解为是多个普通DAE的级联,一个具有两层中间层的深度神经网络结构。DDAE结构如图4所示。

图4 DDAE结构
DDAE结构一般是严格对称的,即为将上一层的编码输出结果作为下一层编码的输入,大大提高运行效率,可以让网络学习到更多的信息,并且将中间层的神经元个数进一步降低,使特征融合的效果大大增强。
2 交流接触器全寿命试验及特征提取
2.1 交流接触器全寿命试验
试验平台按照GB 14048.4—2010中的规定进行搭建和试验,在工程的具体应用中,交流接触器绝大部分工况是在AC-4的条件下,以6倍额定电流来接通和分断电路,因此本次试验在AC-4的条件下对CJX2—50型交流接触器进行研究[11]。试验条件如表1所示。试验系统如图5所示。

表1 试验条件

图5 试验系统
2.2 特征提取
交流接触器运行状态的影响因素较多,仅通过传统电参量的特征来反映其工作状态是不够完善的,从理论上分析,通过数据驱动模型进行开关电器剩余寿命预测的研究,所采集的设备运行过程中的特征参数越多,对设备运行状态的表征越准确,剩余寿命预测的结果也会更准确,因此本文通过加入机械参量的特征,对传统方法进行补充,共提取了11个能够有效反映交流接触器运行状态的特征参数,其中电参量特征参数为接触电阻、燃弧时间、燃弧能量、平均燃弧功率、吸合时间、释放时间;机械特征参数为弹跳时间、触头碰撞速度、分闸速度、超程、开距。电参量特征参数原始数据及变化趋势如图6所示;机械参量特征参数原始数据及变化趋势如图7所示。

图6 电参量特征参数原始数据及变化趋势

图7 机械参量特征参数原始数据及变化趋势
3 算例分析
本文在最大程度上提取了能够影响接触器运行状态的特征参量,其中电参量相关特征6个,机械参量相关特征5个,共11组特征作为数据集,进行多维特征融合仿真。深度降维自编码多维特征融合整体流程如图8所示。

图8 深度降维自编码多维特征融合整体流程
3.1 确定信噪比
仅采用基本自动编码器学习输入特征的信息进行特征融合,很容易产生过拟合现象,并且研究者们普遍认为,能够从经过“损坏”的原始特征中进行特征融合学习后,还能还原出原始特征,这样的网络才是优秀的,经过降维后的融合特征能够最大程度地保留原始特征所包含的信息。因此,本文采用DAE对交流接触器特征参数进行特征融合研究。
对原始数据进行“损坏”就是对网络的输入加入随机噪声,本次采用对原始特征数据进行随机置零的方式进行加噪处理。首先将网络的中间层结构设为一层,中间层神经元的个数设为一个,再依次改变信噪比的数值,进行模型训练,计算并比较输入的原始特征与输出的还原特征之间的误差值,当误差降到最小时,确定信噪比的数值。各信噪比下误差值如图9所示。

图9 各信噪比下误差值
通过图9可以清晰地观察出,当信噪比为0.2时,只有第6个特征的误差大于在信噪比为0.3时,在其余各种情况下,各个特征在信噪比为0.2时,误差均为最低;因此,本文采用的DAE特征融合模型的信噪比取为0.2。
3.2 中间层神经元个数的选择
确定中间层神经元个数,就是确定特征融合重构后降低到的维度。理论上降低到的维度越高,所包含的原始特征的信息就越多,但是当中间层神经元个数提高到一定值,输入的原始特征与输出的还原特征之间的误差下降变得不明显。因此,此时的中间层神经元个数就是最优融合特征维度。
首先设置网络中间层神经元个数为1,依次增加中间层神经元个数,进行模型训练,并计算原始特征与还原特征之间的误差。各种中间层神经元个数各个特征的还原误差如图10所示;各种中间层神经元个数各个特征的累计误差如表2所示。

图10 各种中间层神经元个数各个特征的还原误差

表2 各种中间层神经元个数各个特征的累计误差
通过图10和表2可以观察出,当中间层神经元个数从1增加到3和从3增加到5,误差都会大幅度下降,而当中间层神经元个数从5增加到7时,误差几乎没有下降。因此,本文最终确定的融合重构的特征为5维。
3.3 DDAE层数的构建
神经网络虽然有强大的学习能力,但是单层的神经元结构的学习能力毕竟有限,增加神经网络的层数可以大大提高模型的学习能力和效率。不同层数模型的损失函数如图11所示;不同层数模型的误差值如图12所示。由图11可见不同DDAE模型在训练过程中损失函数的下降趋势。由图12可见各特征还原特征与原始特征之间的误差。

图11 不同层数模型的损失函数

图12 不同层数模型的误差值
通过图11和图12可以观察出,当DAE层数为2时,在迭代10次后,损失函数就能降到最低,而层数为1时要迭代到20次才能降到最低,并且大于层数为2时,由于每次都加入了噪声,当层数为3时,第二层的输入破坏太大,导致损失函数不能下降到理想范围,误差较大,因此本文将DDAE的深度确定为2层,11个特征平均误差值为0.000 2,表明融合后的特征几乎能表达原始特征所有的信息。
4 结 语
交流接触器运行状态特征的提取是实现对其剩余寿命精确预测的必要前提,本文基于DDAE,提出了一种特征融合降维的方法,得到了如下结论:
(1)通过提取交流接触器的机械特征参数,对仅考虑电参量的研究方法进行特征补充,较为全面地对其运行状态进行表征。
(2)提取的特征越多,表征能力越强,但是考虑到后续剩余寿命预测模型的输入量维度越大,训练难度和计算量成指数上升,故要以较少的输入特征在最大程度上反映交流接触器的运行状态。
(3)通过确定DDAE中间层数和神经元个数,构建交流接触器特征融合降维模型,结合试验数据,将11维的特征融合重构后降到了5维,并且误差在10-4数量级,证明本文提出的方法可行有效,为后续对交流接触器剩余寿命预测研究夯实了基础。
