机器学习和深度学习的并行训练方法

祝佳怡

（西南民族大学计算机科学与工程学院，成都 610225）

0 引言

人工智能（artificial intelligence，AI）这一概念的出现最早可以追溯到20世纪50年代。随着Marvin Minsky和John McCarthy于1956年共同主持的达特矛斯会议（dartmouth summer research project on artificial intelligence,DSRPAI）的举办，“人工智能”这一概念被正式定义。该会议的举办标志着人工智能进入了第一次发展期。在当今时代，因机器学习（machine learning,ML）和深度学习（deep learning,DL）方法和大数据技术的不断发展，人工智能已经成为必不可少的科学技术之一。如今人工智能模型的效果越来越好，这离不开高性能模型的设计，而无论是在工业界还是学术界，机器学习方法及深度学习模型都越来越倾向于向更复杂的方向发展。这一发展趋势使得模型的训练成本越来越大，再加上数据量的庞大，训练一个效果优秀的深度学习模型往往需要数月的时间。

在一般的计算机程序中，解决问题的算法通常是以指令序列流的形式执行，这些指令通过中央处理器（central processing unit,CPU）来进行计算，这种方法被称为串行计算（serial computing）。与之相对的并行计算（parallel computing）则将一个任务划分为互不相关的多个计算部分，并使用多个计算单元对这些计算部分并行地分别进行计算，最终将结果汇总起来，实现了性能的提升。在理想的情况下，并行化所带来的性能提升是指数级别的，即把问题规模划分为一半，性能提升两倍，以此类推。但是在更一般的情况下，并行计算的性能提升遵循Gustafson法则。消息传递接口（message passing interface,MPI）是实现并行计算的一种主流方式，各个进程间通过这一接口来进行任务的分配、消息的接收发送等机制，实现并行的目的。随着目前云服务器和大数据的普及，并行计算将是解决大规模方法的最有效优化手段之一。

传统的ML、DL模型的训练方法是对训练样本一个一个地进行计算，并根据所有样本的结果对模型进行调整。这是一种非常典型的串行的实现思路。通过对该问题进行简要分析可知，每个训练样本之间的计算都是独立的计算单元，这些样本自身的计算之间互不相干，因此可以使用并行化的思想来解决该问题，从而大幅缩减模型的训练时间。多个节点并行地计算各自的样本子集结果，并将这些结果汇总到主节点中，对模型的参数进行更新，完成了一轮的训练流程。在本实验中尝试将这一思想应用于最简单的机器学习模型训练当中。理想情况下，随着计算节点数量的增加，训练所消耗的时间应逐渐减少。实验结果表明，在模型的规模较小时，使用MPI技术实现并行化方法的训练时间会随着节点数的增加而增加。通过分析可知，在各节点的消息接收和发送阶段也会存在一定的时间消耗。如果一个样本计算所消耗的时间小于进程间消息接收发送的时间，则会导致这一与理想情况相悖的现象发生。本实验中的模型是最简单的线性回归模型。在实际中，深度学习模型是非常庞大且复杂的。在这种常规的情况下，一个样本计算所消耗的时间会大幅度多于进程间的通讯时间，这时并行化所带来的计算效率的收益是巨大的。

1 数据集准备及方法介绍

1.1 数据集

本文以回归任务作为示例，并使用其中最基础的线性回归来解释本文阐述的ML、DL并行训练思想。所使用的数据集是随机生成的用于线性回归的数据。数据集的生成使用基于Python语言的Sci-kit Learn工具包中的make_regression（）函数来实现，代码段如下：

其中指定了样本数量为500，特征数量为1。生成的是一个长度为500的向量，也是一个长度为500的向量，中的每一个元素都通过一个参数与中的对应值进行匹配。该数据集的可视化如图1所示。需要注意的是该可视化虽然在视觉上是一条直线的形式，但实际上是由500个数据点构成的。

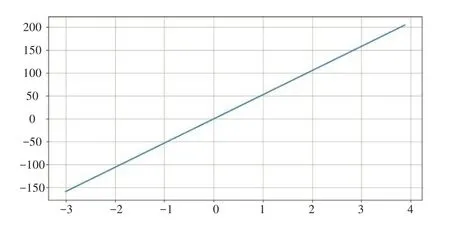
图1 随机生成线性回归数据集的可视化

机器学习及深度学习模型的目标就是找到最好的拟合数据的参数，实现对训练集的特征学习。图2很好地展示了不同的模型或不同的模型参数的拟合情况。

图2 对数据集不同的拟合情况（长线段表示原始的数据集，点线表示拟合情况）

从图2可知，（a）和（b）均没有很好地拟合数据集；而（c）是一个拟合较好的情况，因此本文要尽可能使我们的模型达到如图2（c）所示的效果。

1.2 串行的实现思路

为了更好地阐述以上的问题，在这里给出一些数学符号来对问题进行定义。设训练集的样本总容量为，每个样本含有个特征，则给定训练集∈R，其对应的标签∈R。在上述的数据集中，每个样本只有一个特征，即=1；且保证了本实验中的数据集中所有样本的平均值为0，因此可以用一条=的直线来对数据进行拟合。

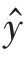
值越小，证明模型对该样本的预测效果越好。对所有样本都进行该运算，最后将所有样本的值进行累加，得到模型总的损失。总损失也被称为模型的代价（cost value）。

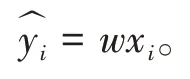
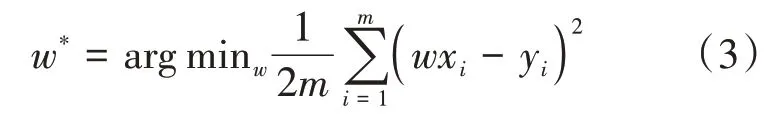
一种通用的求解的方法被称为梯度下降法。根据模型的代价，对参数求偏导，可以使用该值对模型的参数不断进行更新迭代，数学定义如下：

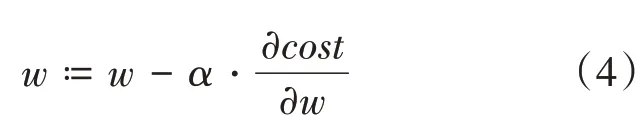
其中为学习率，可以用来调节更新迭代的步长大小。合适的学习率可以使模型的损失更快速地收敛到局部或全局最小值。迭代更新多次后，模型的损失逐渐收敛，不再减小，这时可以认为模型已经训练完毕，此时的参数为模型训练的最终结果。

上述的步骤中，对所有的训练样本是一个一个地进行计算损失，并进行累加作为模型的代价，最终使用梯度下降法进行更新。对训练样本分别进行计算是一个典型的串行思维方式。该思路的伪代码实现如下：

串行的梯度下降算法

假设计算每个样本的预测和计算梯度的时间复杂度为()，则训练一轮需要的时间复杂度为(×)，其中是训练样本的数量。通常情况下()的规模是十分巨大的，又由于训练样本数量通常也有很大的规模（＞10），采用这种串行的计算方式会导致训练大型深度学习模型的时间开销过于庞大。

1.3 并行思想

通过上述的训练过程可以知道，模型的代价计算是一个求和的过程，是对所有样本的损失值进行累加，进而进行更新迭代。在该求和的过程中，每一项（样本的损失值）的计算并不会相互影响，因此每个样本计算损失的过程可以被多个进程或多个计算节点并行化。因此模型的训练过程与最简单的数列求和背后的逻辑是一致的。由于进程之间没有相互依赖，该问题可以很好地被并行化。

根据这一思想，本实验提出的并行训练方法与简单的数列求和思想非常相近。考虑一个数列求和的并行化问题：1+2+…+100，假设由四个节点来计算，一种巧妙的方法是令：

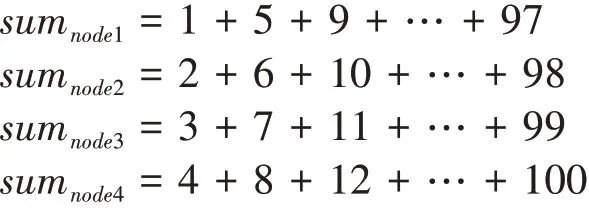
可以看到四个节点分别计算各自的和，并且能够覆盖1…100的所有值。回到模型的训练问题，模型训练中的关键是进行模型的代价，而代价是所有样本的损失值的累加和。因此：

用与数列求和相似的思路可以很好地解决该问题的求解。本实验的机器学习及深度学习模型梯度下降的并行训练算法的伪代码如下所示：

并行的梯度下降算法

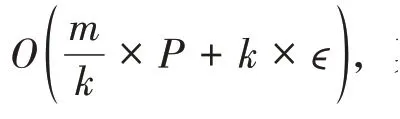
2 代码实现

本节阐述了上述方法的具体代码实现过程。首先是MPI的初始化部分：

初始化后进行数据的读入部分。在这里已经将数据集分别存入X.in和y.in文件中，读入数据的代码如下所示：

指定一些其余的参数，如训练样本数量等，如下所示：

接下来是训练环节。判断当前节点是否为主节点，如果不是主节点则计算后传给主节点，如下所示：

上面的代码中，变量predict为预测结果，loss为损失值，node_derivative为梯度信息。计算完毕后使用MPI_Send（）将梯度信息和损失分别用不同的标识符发送给主节点。主节点部分的代码如下所示：

主节点在计算完自己的部分后，接收来自其他节点的梯度信息和损失信息，并进行累加。累加后求得总损失和总梯度，然后使用weight=weight-alpha*derivative进行梯度更新。上述过程循环epoch次，循环结束后训练终止。在最后主节点对训练的结果进行输出：

需要注意的是，在第一轮循环结束后，主节点要把更新后的weight传给其他节点，其他节点接收更新后的weight后再进行下一轮的计算。主节点发送weight的代码如下：

其他节点接收weight的代码如下：

其他节点在第一轮的训练中，使用0作为参数进行计算，后续的迭代过程中，使用主节点发送的weight来进行计算。以上便是并行训练的核心代码部分。

3 实验结果

在本节中，为了分析并行方法在线性回归模型中所带来的性能提高程度，分别设置了节点数为1，2，4，8，16，32。为了得到可靠的结果，每个节点数量都分别运行了五次。对方法的性能评估主要是用以下三个指标：运行时间、计算所得的参数值、训练300轮后的损失值。将五次的运行结果取平均值和方差，作为最终结果。实验结果如表1所示。

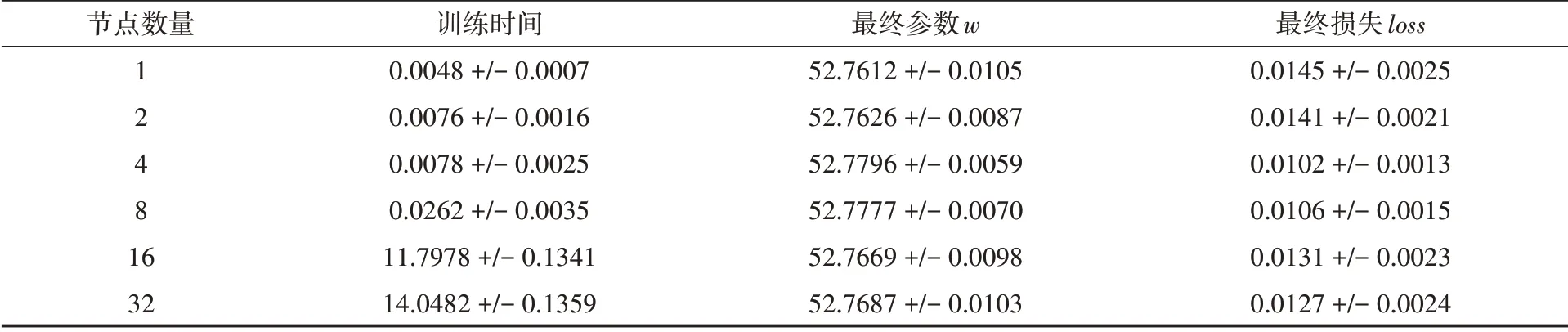
表1 不同节点数量的各个指标统计结果

将模型的参数进行可视化，得到如图3所示的结果。从图中可以看出，预测结果很好地拟合了数据集（点线表示的预测结果与数据集完全重合）。

图3 训练的参数可视化结果

4 分析与讨论

根据表1的结果可以了解到，不同的节点数量训练后最终的参数和最终的损失都保持基本一致。训练的最终效果是一致的，都能拟合到最优的情况。但是训练的时间却出现了与理想情况相悖的现象：随着节点数量的增加，模型所需要的训练时间越来越多。然而理想情况应该是随着节点数量的增加，训练时间越来越少。

这一现象的产生可以从并行方法的时间复杂度进行考虑。在第二节中提到过，并行训练的时间复杂度形式为

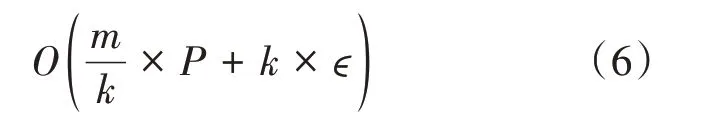
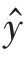
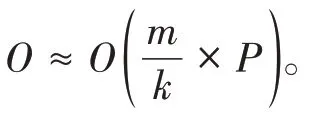
5 结语

在本实验中针对机器学习和深度学习模型的训练过程提出了一种并行化的策略，用于解决大规模的数据和大量的计算所带来的时间消耗问题。本实验以最基础的线性回归作为示例，展示了并行训练的一种思路。对实验结果进行分析，说明基于MPI技术的并行化方法有它的适用场景，也存在不适用的情况。本实验提出的并行化方法适用于大规模的数据集和大规模的网络框架，随着节点数量的增加，训练耗时将大大减少；而对于小规模数据和小规模模型的情景，随着节点数量的增加，训练时间将逐渐增加，因此该并行化方法不适用于此场景。