新型变刚度电液串联弹性机械臂振动控制仿真研究

2022-09-20刘一扬郑香金王良文

机床与液压 2022年10期

刘一扬，郑香金，王良文

(1.郑州财经学院智能工程学院，河南郑州 450000；2.河北轨道运输职业技术学院机电系，河北石家庄 050000；3.郑州轻工业大学机电工程学院，河南郑州 450002)

0 前言

机械臂是机器人领域中广泛采用的一种机械装置，能够替代人类手工劳动，完成各种危险和有害的工作任务，从而提高生产效率。机械臂的迅速发展，也会推动国家经济的发展。未来要实现无人化工厂，机械臂是必不可少的一项，具有广阔的应用前景。串联机械臂在生产中的应用较为常见，是一个典型的非线性驱动系统，拥有多输入、多输出参数，这也使得机械臂运动控制问题变得较为复杂。与发达国家相比，我国在机械臂领域研究起步较晚，还存在一定的差距。机械臂先进技术往往掌握在发达国家手中。因此，必须不断深入研究机械臂非线性控制系统，优化其控制性能，赶超发达国家先进技术，打破其技术垄断。

串联机械臂关节较多、响应速度慢，导致运动误差和振动幅度较大，许多科研人员从不同方向对其展开研究。例如：文献[3-4]研究了串联机械臂关节位置PD控制方法，建立平面两连杆机械臂模型，给出了机械动力学模型，设计了PD控制率，对控制系统的稳定性进行了证明，搭建仿真平台对机械臂关节运动轨迹进行仿真，从而提高了机械臂关节位置控制精度。文献[5-6]研究了串联机械臂神经网络控制方法，建立了三连杆机械臂简图，采用神经网络控制器，引用混合粒子群算法优化神经网络控制器，给出了串联机械臂优化后的神经网络控制结构，采用MATLAB软件对控制系统跟踪误差进行仿真，提高了控制系统的稳定性。文献[7-8]研究了串联机械臂模糊滑模控制方法，给出了机械臂动力学方程式，设计了模糊滑模控制系统，采用李雅普诺夫函数对控制系统的收敛性进行了证明，通过仿真验证两关节机械臂跟踪误差，能够按照预定轨迹进行跟踪。以往研究的串联机械臂控制系统抗干扰能力较差，抖动幅度较大，其控制精度很难满足当今社会发展的要求。对此，本文作者研究了变刚度串联机械臂控制系统，推导出机械臂液压驱动非线性方程式。为了提高机械臂抗干扰能力，设计了反演自适应模糊滑模控制器，通过滑模控制、反演技术和自适应模糊方案控制机械动力学和液压动力学两个回路。采取MATLAB软件对机械臂运动轨迹进行仿真，对比传统滑模控制器的输出效果，为以后进一步研究串联机械臂非线性控制系统提供参考。

1 电液串联弹性机械臂

1.1 机械臂设计

电液串联弹性机械臂系统如图1所示，系统硬件主要包括3个部分：液压系统、机械系统和变刚度执行器系统。液压系统由齿轮泵、交流电机、储液罐、比例伺服阀和单个液压缸组成。交流电机以恒定速度运行，以保持所提供的压力始终处于所需的工作值。伺服阀提供压力油，在气缸上产生所需的扭矩/位置。变刚度执行器系统是串联弹性机械臂和可调弹簧底座机构的组合，如图2所示。可调弹簧底座机构采用滚珠丝杠作为直线运动执行机构，能够处理高精度定位的大负载。作用在第二个连杆上的耦合扭矩对于螺母的每个位置都有不同的值。直流电机驱动滚珠丝杠提供所需的刚度。

图1 电液串联机械臂

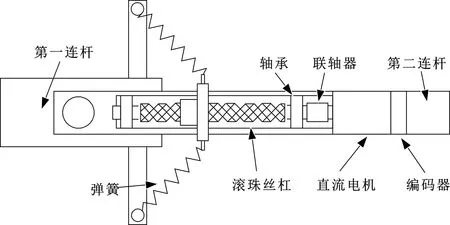
图2 变刚度执行器

1.2 电液伺服系统数学模型

根据液压系统原理，阀内流体流动分布的非线性控制方程定义为

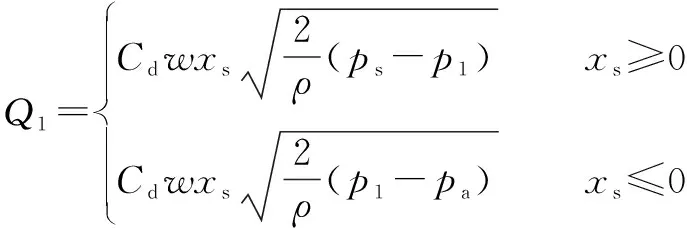
(1)

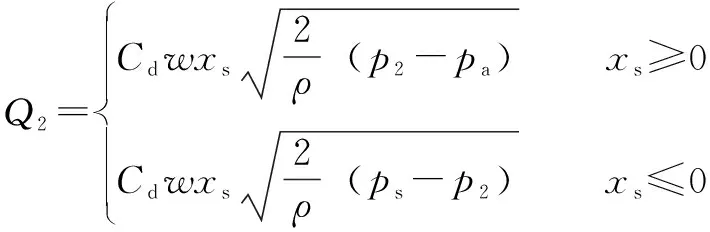
(2)

式中：、分别为流体流入和流出阀门流量；为孔板流量系数；为流体的质量密度；为泵压；为回流压力；、为腔室压力；为伺服阀的面积梯度；为伺服阀的滑阀位移。

液压油通过气缸的连续性方程如下：

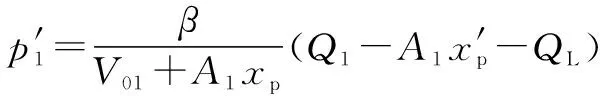
(3)

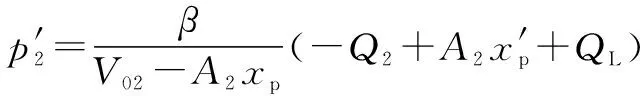
(4)

式中：为液压缸位移；为液压流体的有效体积模量；、为执行机构两侧初始液体体积；、为执行机构两侧面积；为内部泄漏。

滑阀位移与输入电压关系式为

(5)

式中：为滑阀位移增益；为伺服阀输入电压。

1.3 动力学模型

双连杆机械臂动力学方程式为

()″+(,′)+()=-

(6)

式中：()为对称正定机械手惯性矩阵；(,′)为向心力矩和科里奥利力矩矢量；()为重力力矩矢量；为控制力矩矩阵；为外部干扰矩阵。

机械臂第一连杆角度和液压缸位移之间的关系可以表示为

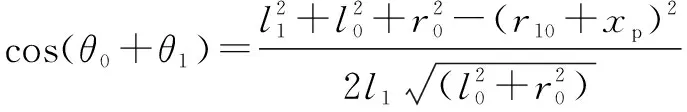
(7)

其中：=+，当=0，为液压缸体的长度。

液压缸产生的第一励磁转矩可通过以下公式计算：

=c=sin=sin(-)

(8)

其中：cos= (+--)2。

第二扭矩和耦合扭矩计算公式为

=(sin-sin)

(9)

=(sin-sin)(+)

(10)

扰动转矩矢量可通过以下方式获得：

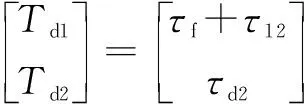
(11)

式中：为外力矩和未知函数；为液压摩擦力矩。

系统的状态变量定义为=[]=[′]，可以用下列状态空间来描述：

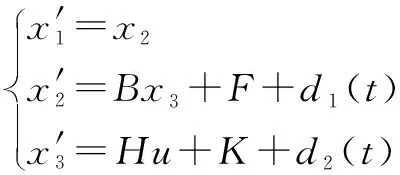
(12)

式中：、、、、()、()为已知函数。

2 控制器设计

对于振动抑制和位置控制，所提出的控制包括两个主要部分:第一种是内环控制，为伺服阀产生电压，以保证等效位置跟踪所需位置,该控制回路还分为两个控制器：位置控制和虚拟转矩控制;第二个部分是外环控制，它重新生成成形位置基准以抑制振动，称为“振动控制”。控制器结构如图3所示。

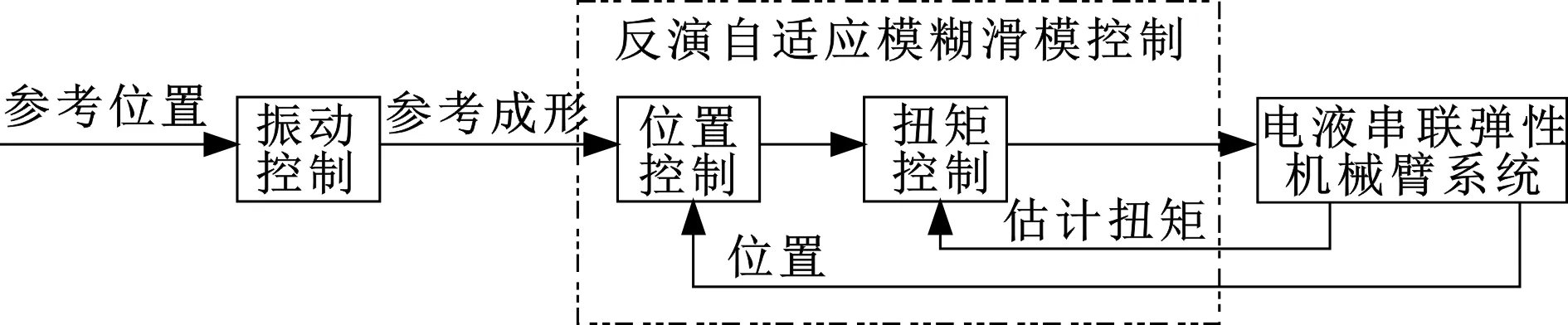
图3 控制器结构

2.1 控制器

(1)反演模糊滑模控制器

第一步：设计滑模控制器，保证跟踪位置误差尽可能小。此步骤将生成虚拟扭矩。选择滑动面为

(13)

式中：为一个非零正常数；第一和第二状态变量的跟踪误差：=-；=-。

式(13)的时间微分方程为

′=′+′=′+++()-′

(14)

将转矩跟踪误差定义为

(15)

不考虑不确定性(()=0)，根据′()=0可导出等效控制力的解，如下所示：

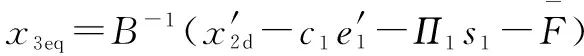
(16)

式中：为正常数。

Lyapunov候选函数的选择如下：

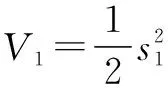
(17)

其导数导出为

′=[′+(+)++()-′]

(18)

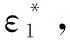
规则2：如果为0，则为;

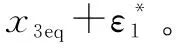
位置控制回路的控制输出可以表示为

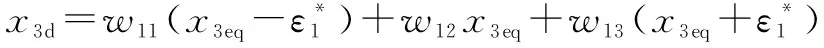
(19)

式中：0≤≤1、0≤≤1、0≤≤1为激励强度。

根据三角隶属函数的特殊情况，关系式++=1是有效的。因此，可以得到：

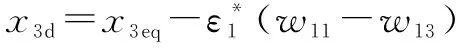
(20)

通过将等式(16)和(20)替换为等式(18)，Lyapunov函数的导数重写如下：

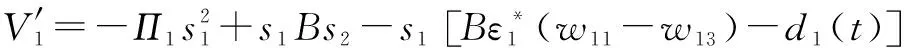
(21)

很明显，如果近似等于零，则跟踪误差将收敛到零。因此，下一步是控制转矩误差尽可能小。

第二步：设计虚拟转矩控制回路，保证跟踪误差接近于零。取式(15)的时间导数为

′=++()-′

(22)

在不考虑不确定性()的情况下，选择控制信号作为′()=0的解，如下所示：

=(-+′--)

(23)

式中：为任意的一个正常数。

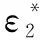
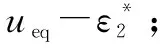
规则2：如果为0，则为;

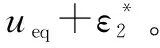
虚拟转矩控制回路的控制信号可以表示为

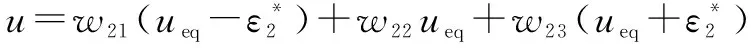
(24)

式中：0≤≤1、0≤≤1、0≤≤1为激励强度。

根据三角隶属函数的特殊情况，关系式++=1是有效的。因此，可以得到：

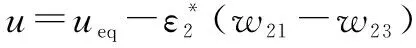
(25)

将整个系统的Lyapunov函数定义为

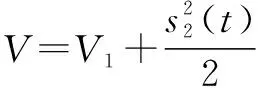
(26)

则式(26)对时间导数为

(27)

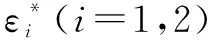
(2)反演自适应模糊滑模控制器

第一步：在位置控制回路中，平移宽度的自适应控制。

平移宽度的估计误差定义为

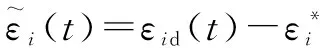
(28)

式中：d()为理论平移宽度的估计值。

对于位置控制回路，虚拟转矩可以表示为

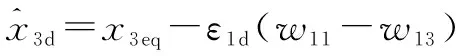
(29)

因此，Lyapunov候选被重新选择为

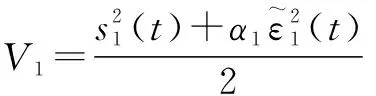
(30)

式中：为正常数。

的时间导数的最终形式如下所示：

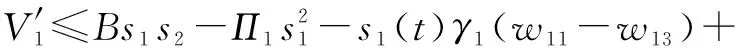
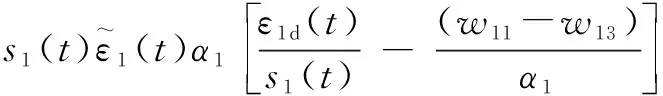
(31)

第二步：在虚拟转矩控制回路中应用平移宽度自适应律。

将整个系统的Lyapunov函数看作：

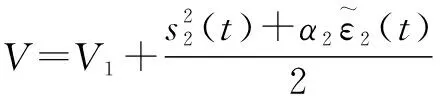
(32)

式中：为微小正常数。

控制信号重新定义为

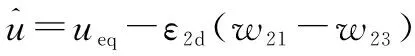
(33)

的时间导数的最终形式如下所示：

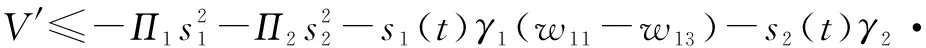
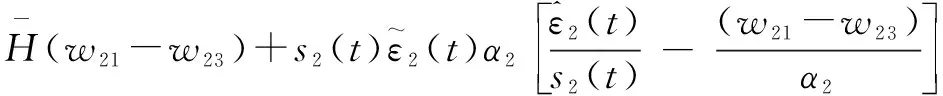
(34)

如果两个回路的自适应律设计为

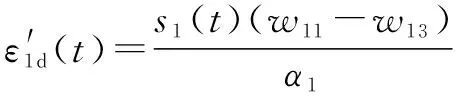
(35)

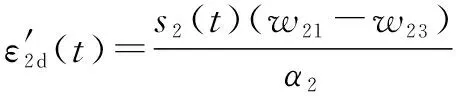
(36)

因此，式(34)变为

(-)

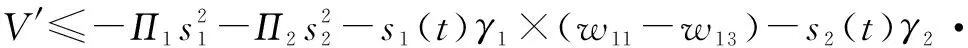
(37)

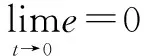
2.2 模糊输入整形的设计

将输入成形技术与模糊逻辑相结合，提出一种振动控制方法。当刚度调节改变系统特性时，利用模糊引擎调整输入成形技术的参数。采用零振动和零振动导数两种输入整形器来抑制末端执行器的振荡。

(1)输入整形器

提出一种零振动整形器来抑制残余振动，其形式可以表示为

()=[e- +e- ]()

(38)

参考信号()由4个参数形成两个脉冲序列：脉冲和的大小以及延迟时间和。为了在最后一次冲击后实现零振动，这些参数如下所示：

(39)

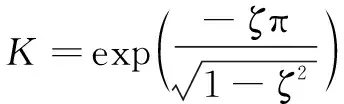
(40)

式中：为系统的阻尼频率；为阻尼比。

(2)模糊输入整形

在此研究中，变刚度执行器可随系统参数(和)在较宽范围内调整刚度。在机械臂刚度调节过程中，设计了模糊输入成形，对输入成形参数进行更新，使估计值与实际值接近。模糊逻辑系统由模糊化、去模糊化、模糊规则和模糊推理机组成，如图4所示，具有2个输入和3个输出。

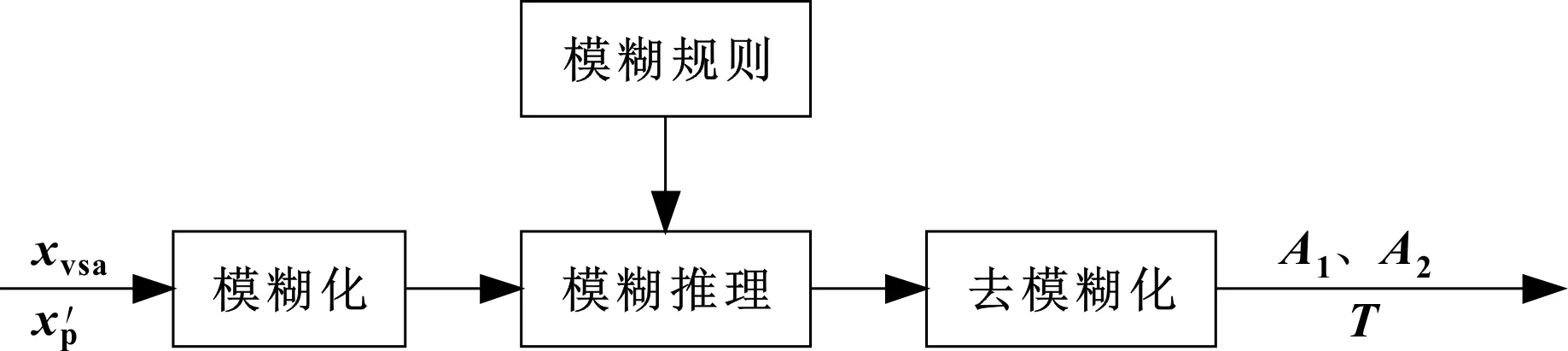
图4 模糊逻辑系统

输入是滚珠丝杠的位置和液压缸速度′。位置和速度的隶属函数分别为模糊集为的三角隶属函数和模糊集为正(P)和负(N)的梯形隶属函数。输出是零振动的3个参数、和。它们是三角隶属函数，模糊集扩展(E)和收缩(R)用于(=1,2)输出，模糊集(=1,2,…,10)用于输出。模糊化器用来对变量进行缩放，并将其转换为语言变量。采用乘积推理和中心平均解模糊器，计算模糊系统的输出。

3 结果与分析

通过MATLAB软件对电液串联机械臂所采用的反演自适应模糊滑模控制器进行验证，观看机械手第一连杆的角位移、角速度和扭矩变化情况，并且与传统模糊控制器进行比较。仿真参数设置见表1。

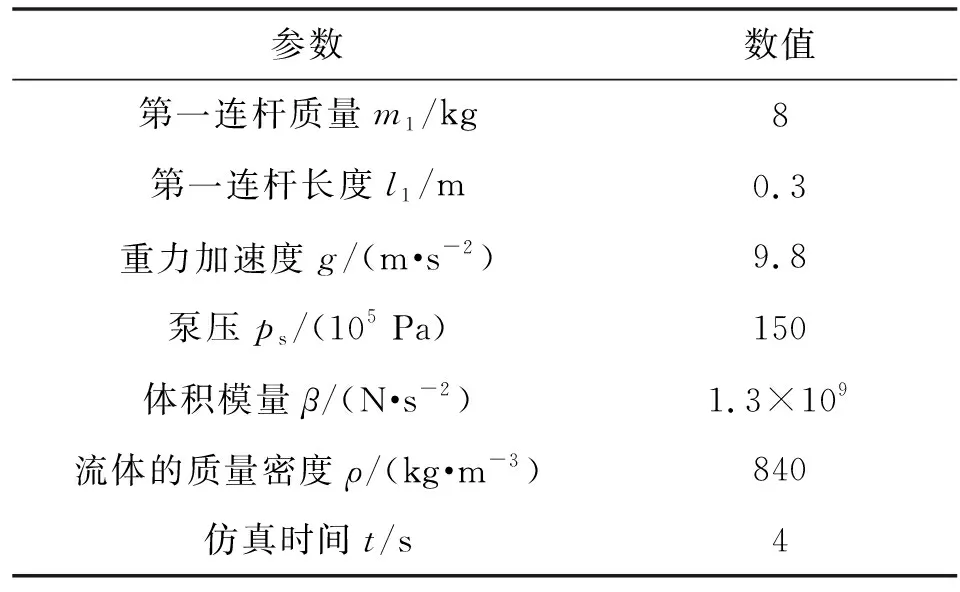
表1 仿真参数

假设机械臂1角位移为正弦波形(=-20sinπ)，转矩为阶跃波(=0.4 kN·m)。在无干扰环境中，机械臂1角位移、角速度和转矩跟踪结果分别如图5、图6和图7所示。在有干扰环境中，机械臂1角位移、角速度和转矩跟踪结果分别如图8、图9和图10所示。

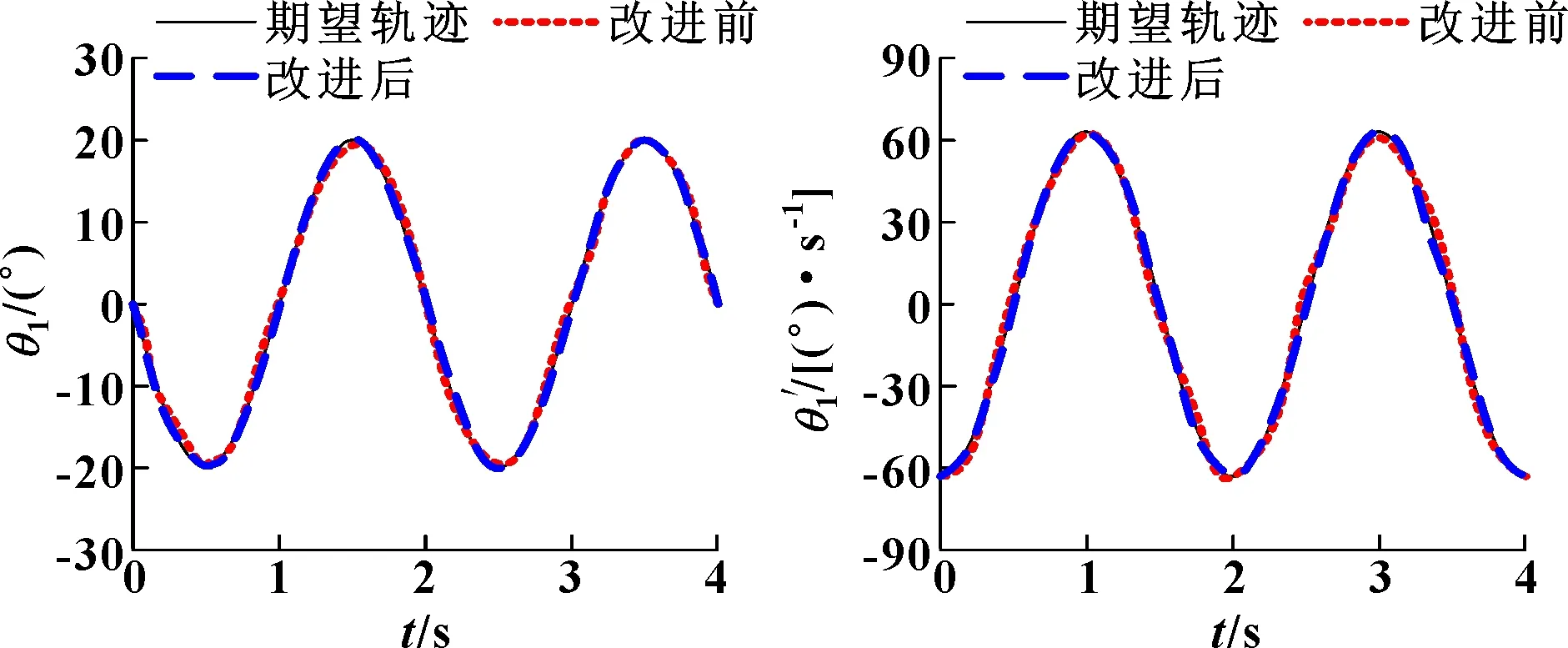
图5 机械臂1角位移(无干扰) 图6 机械臂1角速度(无干扰)

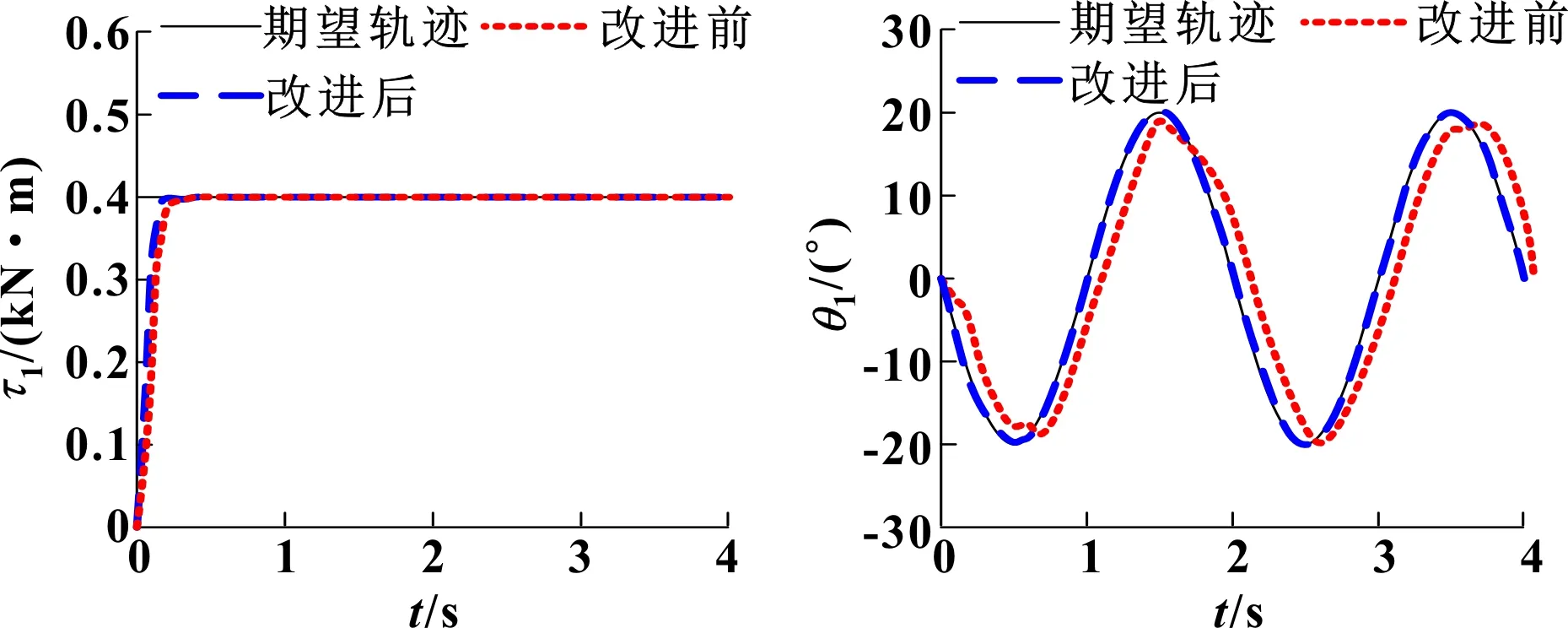
图7 机械臂1转矩(无干扰) 图8 机械臂1角位移(有干扰)

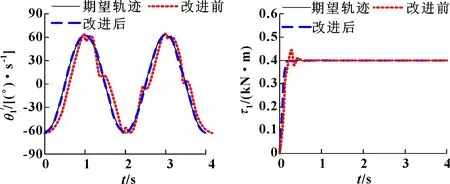
图9 机械臂1角速度(有干扰) 图10 机械臂1转矩(有干扰)

在无干扰环境中，如图5、图6和图7所示：采用滑模控制器(改进前)和反演自适应模糊滑模控制器(改进后)，机械臂1角位移和角速度跟踪误差都较小，转矩控制反应速度较快，无超调量，两种控制器跟踪效果相差不大。在有干扰环境中，如图8、图9所示：采用滑模控制器，机械臂1角位移、角速度跟踪误差都较大；而采用反演自适应模糊滑模控制器，机械臂1角位移和角速度跟踪误差都较小。如图10所示：采用滑模控制器，机械臂1转矩跟踪反应速度较慢，在0.48 s后处于稳定状态，超调量为10%;而采用反演自适应模糊滑模控制器，机械臂1转矩跟踪反应速度较快，在0.15 s后处于稳定状态，无超调量。因此，在相同环境中，采用反演自适应模糊滑模控制器，能够抑制外界波形对机械臂控制系统的干扰，不仅可以提高机械臂的跟踪精度，而且还可以抑制机械臂的振动幅度。