考虑增材制造倾角约束的结构拓扑优化方法

0 引言

拓扑优化因其不依赖于初始结构及工程人员的经验，可以获得满足优化目标的创新构型

。然而，拓扑优化得到的几何构型往往比较复杂，采用传统的减材制造工艺加工十分困难甚至可能无法制造

，增材制造技术采用特殊的制造工艺，可以制造出构型复杂的结构，推动了拓扑优化技术的应用。但增材制造技术受限于其层层堆叠的制造原理，将要打印的结构只有被完全支撑才能打印出来，在宏观上表现为结构的倾角必须不小于设备可打印倾角的临界值，否则会在制造的过程中出现坍塌现象，无法得到所设计的结构。需要指出的是，不同设备和工艺可打印倾角的临界值不同，通常大于40度

。针对上述问题，Wu等以需要打印的模型为边界，控制菱形网格的长宽比及结构的最小壁厚，使其满足增材制造的工艺要求，最终得到以菱形结构为单胞填充模型的拓扑构型

。Brackett等在拓扑优化设计中，对倾角不能满足自支撑的杆件进行惩罚处理，优化得到需要支撑材料最少的拓扑构型

。

从现有的研究成果分析发现，目前主要考虑的方法是减少支撑结构，但是后期的拆除过程中可能会影响原始结构的质量和性能，而存在于结构封闭内部的支撑结构无法被拆除。因此，本文从微观角度出发，基于增材制造层层堆积的原理，建立满足增材制造倾角约束的单元密度更新迭代规则，以结构的柔度最小为优化目标建立数学模型，对优化模型进行求解，得到了具有倾角约束的拓扑构型。通过典型算例和实验对所提出的方法进行验证。

1 增材制造倾角约束的结构拓扑优化设计

1.1 考虑增材制造倾角约束的单元密度更新迭代规则

如图1所示为矩形的设计区域，将其均匀离散

×

为个单元，每个单元均与初始密度变量

(

,

)关联，每个单元的可打印密度

(

,

)与其初始密度

(

,

)相关，其中

和

分别表示单元在竖直方向和水平方向的位置，

方向为打印方向，第一层位于基底上，该层的索引号为

=1。根据增材制造层层堆叠的原理，位于(

,

)处的单元只有被已打印层充分支撑才可打印。每个单元的支撑区域为

(

,

)，支撑区域

(

,

)为该单元正下方及其相邻的各个单元组成。

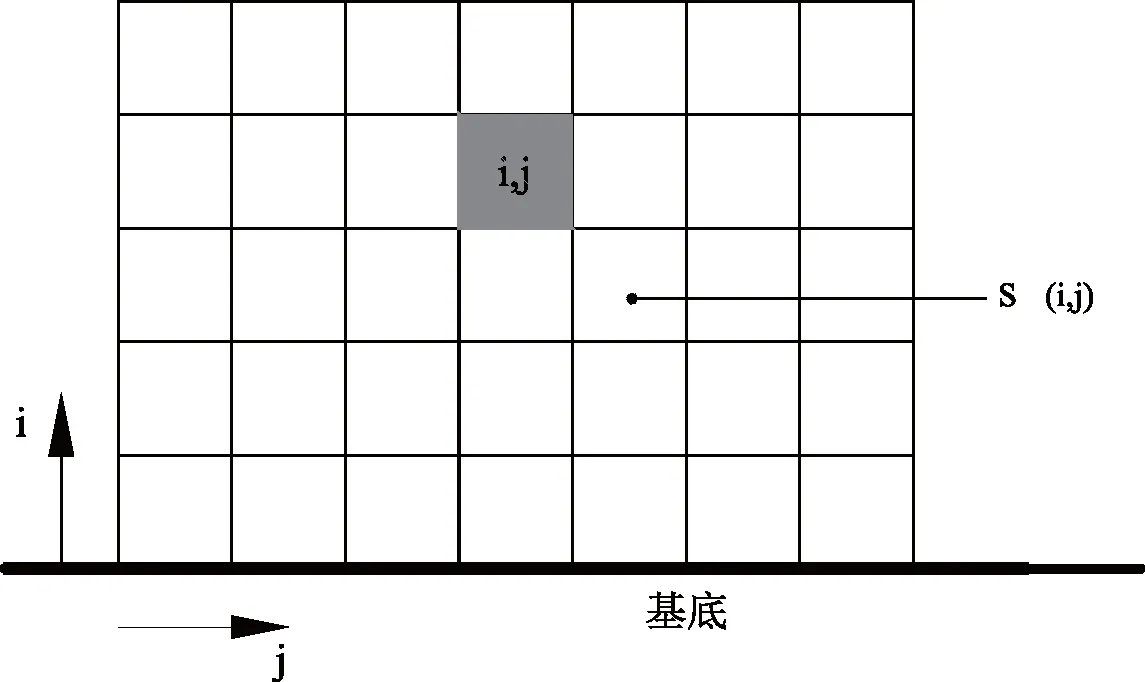
依靠基底支撑的单元(

=1)都可以直接打印，对于

>1层的各个单元被完全支撑，每个单元的可打印密度为：

我在寻访团中年龄最小，同学们都是一些95后。突出的困难就是没有改革开放40年的完整经历，没有在社会工作的真实体验。

对上述问题，可以通过如下的加权求和的办法修正校验．设UPC加权求和的权数为(ω1,ω2,…,ω12)=(3,1,3,1,3,1,3,1,3,1,3,1)，可以算得商品项目代码0 8 9 6 0 0 1 2 4 5 6的加权和为

(1)

如图2所示为Michell梁结构的设计域示意图，Michell梁的长为L=180，高为H=90，在梁结构底部下边界中心施加竖直向下的集中力，其中梁结构的左下角固定，右下角简支。

1.2 增材制造的倾角约束

为了便于进行敏度分析，将迭代模型采用光滑近似的可微形式进行表示，定义如下的近似形式：

对60例乳腺癌患者的70个病灶，其中有37个恶性病灶，占据比例为52.85%，即为29个浸润性导管癌、3个导管原位癌、1个导管内乳头状癌、1个小叶原位癌、1个浸润性小叶癌、1个混合癌、1个黏液癌。33个良性病灶，占据比例即为47.14%，15个纤维腺瘤、5个导管内乳头状瘤、5个纤维囊性乳腺病、2个良性叶状肿瘤、1个乳腺慢性炎症、1个放射状瘢痕、1个复合性硬化性腺病、1个重度不典型增生、1个脂肪瘤、1个错构瘤。

(2)

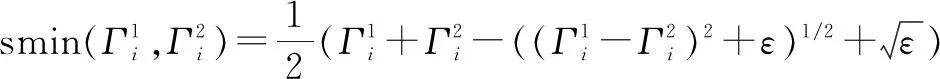
(3)

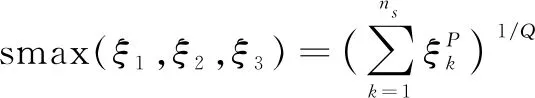
(4)

(4) 模块配置.根据具体需求结合配置规则库,检索出符合设计要求的模块,并对模块进行组合、替换,完成设备模块配置方案.配置规则库的建立需要对企业长期积累的设计经验进行归纳总计.

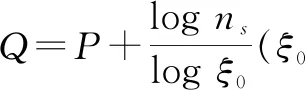
(5)

式中：

是单元支撑区域每一层的单元数，

=3；

和

是调节光滑近似模型的参数。

(

,

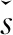
)=smin(

(

,

),

(

,

))

(6)

(

,

)=smin(

(

,

),

(

-1,

))

(7)

(

,

)=smax(

(

-1,

-1),

(

-1,

),

(

-1,

+1))

(8)

(

,

)=smax(

(

-2,

-1),

(

-2,

),

(

-2,

+1))

(9)

因为每个拉格朗日乘子矢量均由其上面两层的相关乘子矢量决定，因此评估的顺序是从上往下逐层进行的，这与瞬态问题的伴随灵敏度分析方法类似，所以：

(10)

所以增材制造倾角约束的模型可以表示为：

2 拓扑优化数学模型及求解

2.1 拓扑优化模型

采用基于固体各向同性材料惩罚模型(Solid Isotropic Material with Penalization，SIMP)

的连续体结构拓扑优化方法，以可打印结构的柔度

最小为优化目标，以增材制造倾角约束和给定体积分数以及力学控制方程为约束条件建立拓扑优化模型如下：

2.1 叶面喷施生长调节剂 对僵苗现象严重的水稻田块还应喷施叶面肥和生长调节剂，如僵苗灵、肥力素、活力素、叶肥王等，以调整植株生理活性，增强抗性，促进水稻的快速恢复生长。

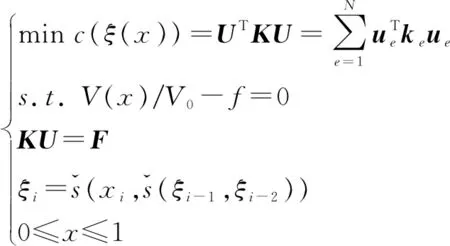
(11)

式中：

为目标函数，即结构的整体柔度值；

为整体刚度矩阵；

为整体位移；

为外载荷矢量；

(

)为结构优化后的体积；

为结构的初始体积；

为给定体积分数；

为结构的倾角约束等式即增材制造的倾角约束。

2.2 灵敏度分析及模型求解

在式(11)的拓扑优化模型中，目标函数

关于设计变量的敏度表达式为：

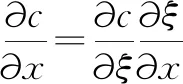
(12)

其中

(13)

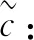
(14)

(15)

式中：smin和smax分别采用式(3)和(4)的近似形式，需要指出的是第

层的可打印密度与第1层到第

-1层的可打印密度均密切相关。为了使敏度求解过程更高效，采用伴随公式表达可打印密度与初始密度之间的关系：

(16)

3 数值算例及实验

3.1 Michell梁数值算例

式中：

(

,

)为每次迭代后(

,

)处单元的可打印密度值；

(

,

)为每次迭代前(

,

)处单元的初始密度值；

(

,

)为(

,

)处单元支撑区域内各单元可打印密度的最大值；

(

,

)为(

,

)处单元支撑区域内各层最大可打印密度中的最小值。

材料的弹性模量为1，泊松比为0.3，集中载荷F=1(所有量均为相对值，无量纲，下文同)，给定体积分数为0.5。基于有限元理论，采用四节点单元将设计域离散为180×90的网格模型，以结构的柔度最小为优化目标，定义水平面为基底，竖直向上为结构的打印方向。单元密度更新迭代规则光滑近似模型的相关参数设定为

=10

,

=40,

=0

5。

分别进行无倾角约束和有倾角约束的Michell梁拓扑优化设计，得到拓扑构型如表1所示，从图中可以看出，无倾角约束和有倾角约束的拓扑构型完全不同，主要表现在有倾角约束的拓扑构型，构件与水平面所成的夹角均比较大，而无倾角约束的拓扑构型，其构件的角度有大有小，甚至存在近似为零的情况，这种完全悬空的结构无法直接进行增材制造。

三要突出围绕农业增效加快农田灌排设施建设，内河圩堤与沿河低洼地内的农田按照 “防洪、挡水、抢排、抽排、降渍、蓄水、引水、提水、调整结构”等思路建设好农田水利综合治理小区，加快内河圩堤和沿河低洼地内的农田水利工程治理步伐；按照“蓄、引、提、调”的要求，以涧沟或小流域为单元大建集“河、库、塘、渠、站、水保”为一体的“长藤结瓜”式的工程，重点建成一批活库、活塘工程，切实提高丘陵区防洪和水源的供给能力，推进以塘坝扩挖、沟河疏浚、集体泵站更新改造（机井建设）和基层水利服务体系建设为主要内容的“三加一”工程建设。

为了更加直观地表现所添加的倾角约束能够控制拓扑结构的最小倾角，分别对无倾角约束和有倾角约束拓扑构型的典型倾角进行测量，角度编号如图3(a)、(b)所示。由于Michell梁的拓扑结构是左右对称的，因此测量任意边的典型倾角即可，本文测量结构右边的典型倾角，各角度值的大小如表2所示。

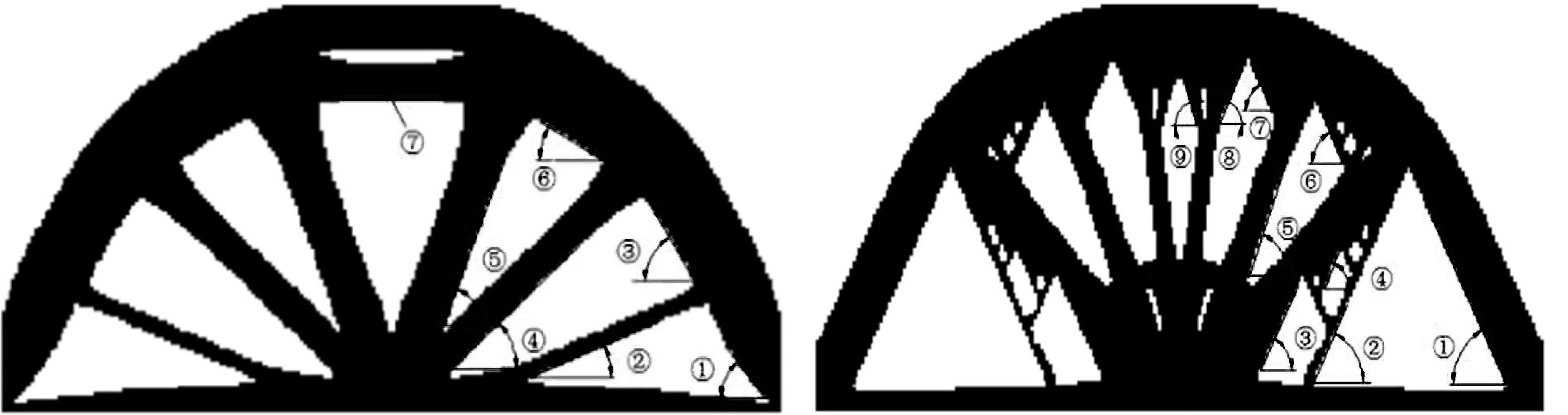
从拓扑构型和实验结果可以得出：无倾角约束拓扑构型结构倾角的范围很大，倾角小于临界值的地方会出现坍塌现象，在打印实验时无法实现自支撑，从而打印失败。具有倾角约束的拓扑结构由于角度均大于63度没有出现坍塌现象，实验结果进一步验证了本文提出拓扑优化方法的可行性，拓扑得到的结构可以直接进行增材制造，实现自支撑。

3.2 实验验证

为了进一步验证本文提出的适应增材制造构件倾角约束的拓扑优化方法的可行性，证明拓扑得到的结构能够直接进行增材制造。分别对有、无倾角约束的Michell梁拓扑构型进行3D打印。设定Michell梁长为120mm，宽为60mm，厚度为10mm，采用熔融沉积成型技术(FDM)对模型分别进行制备，均不添加外支撑结构，表3为模型的打印过程。

最终得到如图4所示的结构，具有倾角约束的拓扑结构由于角度均大于63度没有出现坍塌现象。

综上所述，针对公路进行养护时，不仅需要及时掌握翻浆现象出现的主要成因，同时也需要根据具体情况对导致翻浆现象出现的主要因素和条件加以分析，通过加大排水力度、提升施工管理、及时换填土以及提升养护效率等方式加大对翻浆现象的预防及养护效果，保证公路的正常运行，提升交通安全效率，加速实现我国走可持续发展路线的基本目标。

如图5局部放大所示，无倾角约束的拓扑构型不满足倾角约束的部分，出现了明显的坍塌现象，并且倾角越小的结构坍塌现象越明显。实验结果进一步验证了本文提出拓扑优化方法的可行性，考虑倾角约束的结构可以直接进行增材制造，实现自支撑。

4 结论

遵循增材制造层层堆积的基本原理，从微观角度建立满足增材制造倾角约束的单元密度更新迭代规则，使结构在宏观上满足增材制造的倾角约束。分别对添加和不添加增材制造倾角约束的拓扑构型，采用熔融沉积成型技术对结构进行制备，结果证明提出的方法能够约束拓扑构型的倾角，实现宏观结构的自支撑设计。

[1]刘书田，李取浩，陈文炯，等.拓扑优化与增材制造结合:一种设计与制造一体化方法[J].航空制造技术,2017(10):26-31.

[2]Zhou M, Fleury R, Shyy Y K, et al. Progress in Topology Optimization with Manufacturing Constraints[C]//9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. 2002:1-8.

[3]Wang D, Yang Y, Yi Z, et al. Research on the fabricating quality optimization of the overhanging surface inSLM process[J]. International Journal of Advanced Manufacturing Technology, 2013,65(9-12):1471-1484.

[4]Wu J, Wang C C L, Zhang X, et al. Self-Supporting Rhombic Infill Structures for Additive Manufacturing[J].Computer-Aided Design, 2016, 80:32-42.

[5]Brackett D, Ashcroft I, Hague R. Topology optimization for additive manufacturing[C]//Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, Aug, 2011:348-362.

[6]M. P. Bendsøe, O. Sigmund. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9-10):635-654.