钢弹簧浮置板柔性轨道模态分析

2022-09-20李海涛

内燃机与配件 2022年13期

1 引言

城市的轨道交通建设是政府和市民普遍关心的话题，高效、舒适、清洁是轨道交通相比其他公共交通工具的显著优势，有着非常广阔的应用前景。但是在轨道车辆越来越多的应用于大中型城市交通建设的进程中，会不可避免的带来一些环境影响，这些影响因素也逐渐受到重视，其中最突出的问题便是轨道车辆的振动和噪声

。有效减小轨道车辆的振动和噪声是学术界、制造商和应用方一直在持续研究的重要课题之一。

车辆轮轨不平顺激励是引发车辆振动的直接原因，针对不同激励下轨道及轨下结构的减振效果，已经有前人进行了研究

。现在普遍认为浮置板轨道是非常有效的减振轨道之一。不同形式的浮置板通过一定刚度的连接来分离并减弱轨道上方至道床的振动传递，在国内外地铁轨道实际应用中取得了不错的效果。钢弹簧浮置板轨道是当前最重要的浮置板减振轨道形式之一，已经在我国现代城市轨道交通中得到广泛应用，可以非常有效的衰减轨道以上的振动。国内有不少学者研究过钢弹簧浮置板轨道对于减振的影响：李响、任尊松通过改变钢弹簧浮置板的长度、厚度、垂向刚度及跨度等参数来分析其垂向振动特性

，汪杰通过对钢弹簧浮置板的静力和模态分析进行轨道扣件刚度和钢弹簧垂向刚度的参数优化

，张辉等人进行了车辆轨道耦合动态行为如钢弹簧浮置板轨道结构特殊工况的振动分析

，李响等人还对地铁小半径曲线段的钢轨波磨机理做了研究

，吴磊分析了轨道板间接缝处的动态行为及安装连接措施的影响

，杨尚福等人对特定市域铁路上钢弹簧浮置板的适用性进行分析

，刘立才研究了与隧道相结合的浮置板轨道-隧道-土体耦合系统的动力学刚度、阻尼的响应等

。本文认为研究钢弹簧浮置板轨道刚柔耦合模型较普通车辆钢轨模型新增的频率振型，对于地铁列车高速稳定运行有十分重要的作用。

按照《关于节能新能源车船享受车船税优惠政策的通知》(财税〔2018〕74号)相关要求，工信部官方网站对《享受车船税减免优惠的节约能源使用新能源汽车车型目录》(第一批)名单进行了公示。本次将排量小于1.6L的车型纳入车船税减半政策适用范围，在满足排量要求的同时，车辆还需符合综合工况油耗的相应标准，所以并不是所有1.6L排量以下的车型都可以享受此政策。此外，对于符合新能源产品技术标准以及相关质量要求的纯电动商用车、插电式(含增程式)混合动力汽车、燃料电池商用车，免征车船税，目前市场中绝大部分插电式混合动力车型均在免征范围内，主要包括中国生产的自主、合资车，而进口插混车型不在此范围内。

本文使用有限元软件Hyperworks系列中的Hypermesh进行几何建模、材料设置、属性赋予及单元网格划分；使用Abaqus求解器进行有限元计算；使用车辆动力学软件Simpack搭建车辆-轨道耦合动力学仿真模型，进行特征根分析并提取有效结果。

2 弹性轨道有限元模型

2.1 有限元模型建模

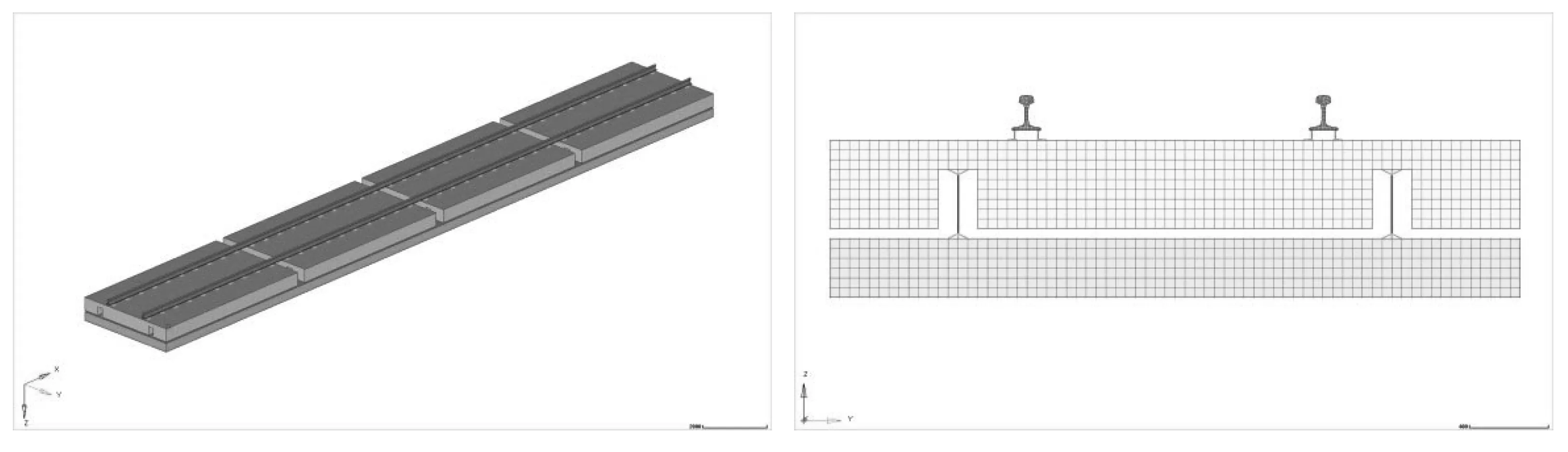
根据实际轨道及轨道板参数，在Hypermesh软件的Abaqus模块下建立带有钢弹簧浮置板的轨道模型。本文搭建的有限元仿真模型沿纵向总长为25m，其中实体单元分为三层，分别是轨道、浮置板以及道床。轨道及道床是贯通的25m，而浮置板共有4块，每一块沿纵向长度为6m。轨道的单元尺寸为10-20mm，浮置板及道床的网格较轨道略为稀疏，单元尺寸设置为50mm。所有的浮置板及道床实体单元均为规整的六面体单元。扣件采用1D bush单元(Abaqus模块下为CONN3D2单元)模拟，每个bush单元两端的节点各自通过0D rbe2单元(在Abaqus模块下为COUP_DIS单元)分别连接上下实体(轨道、浮置板)表面的部分节点(根据模型实际情况为6-9个节点)。浮置板与道床的连接同样采用1D bush单元与0D rbe2单元相结合的方式，通过0D rbe2单元连接到上表面(浮置板)与下表面(道床)实体上各9个节点，以此保证刚度传递的有效性。仔细检查模型所有需要连接的地方是否连接完好。最终有限元软件中的仿真模型共有单元731778个、节点592708个；其中3D单元731298个、节点591988个；1D单元480个、节点240个；0D单元4160个、节点480个。扣件间距为0.625m，钢弹簧间距为1.25m。生成的有限元模型如图1所示。

建模完成的Simpack车辆-轨道动力学模型中，车体、构架、轮对各有6个自由度，即纵向、横向、垂向、侧滚、点头、摇头(其中轮对垂向和侧滚运动是非独立运动)；轴箱体取1个点头自由度(相对于轮对)，中心销取1个摇头自由度。坐标系的规定为沿着车辆前进方向是X轴正方向，以X轴在轨道平面内顺时针旋转90度所指向的方向为Y轴正方向，以垂向轨道平面向下的方向为Z轴正方向。对钢弹簧浮置板与普通钢轨模型的轨道进行分析对比，动力学刚柔耦合模型如图2所示。

2.2 材料属性

模型中钢轨的材料为普通的钢结构参数，轨道板的材料属性参考文献中设置，扣件及钢弹簧的垂向刚度、垂向阻尼及纵向刚度、横向刚度(纵向和横向刚度对于扣件的影响远小于其垂向刚度，本文设置扣件描述单元的纵向刚度与横向刚度相同、纵向阻尼与横向阻尼一致；对于钢弹簧的描述单元与扣件类似)均参考文献设置

。在有限元软件中建立好材料卡片后，与各自的属性卡片关联，然后赋予到相应的各类component部件单元上。

对于25m长的钢弹簧浮置板柔性轨道，模态分析最高频率设置为700Hz，利用Abaqus求解器对Hypermesh生成的完备inp文件进行计算，计算完成后得到odb文件。随后进入Simpack软件中导入odb文件生成fbi文件，利用Linear Flextrack模块由fbi文件最终生成柔性体的body。轨道上方是某型地铁车辆的一节中间车，为无摇枕结构形式。主要包括构架、轮对、轴箱悬挂装置、中央悬挂装置、制动和牵引装置等。轴箱悬挂装置包括转臂定位、轴箱钢弹簧和一系垂向减振器；中央悬挂装置采用空气弹簧模型，安装设置了二系横向减振器，并且设有间隙和橡胶块组成的非线性横向止挡；转向架是采用Z字形牵引拉杆驱动。车辆涉及的各个重心位置、质量、惯量、垂向刚度、横向刚度、纵向刚度、各方向阻尼、摩擦系数等均按照基本参数设置或者通过曲线输入实现。Simpack软件中有丰富的力元库(Force Elements)可以允许用户依据模型的需要选取不同的力元，其中空气弹簧使用83号线性空簧力元(Linear Airspring Cmp)，牵引拉杆使用4号力元(Spring-Damper Parallel PtP)，抗侧滚扭杆使用13号力元(Spring-Damp Rot meas Inp Cmp)，节点使用43号力元(Bushing Cmp)，抗蛇形减振器用6号力元(Spring-Damper Serial PtP)模拟，一系弹簧和横向止挡采用5号力元(Spring-Damper Parallel Cmp)来描述。在需要连接的部位利用joints建立相应的铰接关系，轮对与柔性钢轨之间匹配相应的轮轨关系。

157.4Hz频率为钢轨一阶弯曲和轮对反向侧滚耦合频率，如图3所示。这是引入钢弹簧浮置板柔性轨道后新增的模态特征，左右轨道振型为一阶弯曲且相互错位，而前后轮对的振型为反向侧滚。

2.3 动力学模型生成

相关资料显示，腌制发酵香肠时，通常添加2%左右的食盐，但随着发酵过程的进行，香肠内部水分含量会逐渐减少，食盐浓度会逐步升高，在一般的发酵香肠中，食盐含量可达到5%。因此，欲将鲁氏酵母菌作为发酵剂应用于发酵香肠中，必将考虑其对食盐的耐受能力，本试验测定鲁氏酵母菌的最大食盐耐受浓度为6%。

将合成的降粘型型聚羧酸减水剂PC-A和市售普通减水剂PC-1和进口知名品牌减水剂PC-2进行C60混凝土应用性能对比实验，结果见表2。

3 求解和计算结果分析

人为因素导致网络安全受到威胁主要有两种可能性，第一种可能性是外来的黑客对计算机网络系统进行攻击。第二种可能性是内部人员的非法操作对计算机网络系统带来的威胁。黑客攻击是目前计算机网络所面临的最大问题，也是很多计算机网络安全防范的重点所在。黑客之所以能够侵入计算机系统是因为他们发现了能够利用的漏洞，利用计算机网络本身的不稳定性来满足自己的不法欲望，对用户的财产和隐私安全造成威胁。任何的网络设计都不可能达到完美，内部网络的使用者如果没有强大的安全意识就很容易在操作时出现不当的操作，从而对数据造成损害和破坏，这些状况都很可能对计算机网络系统带来巨大的伤害。

由于车辆运行在轨道上，相当于对轨道增加了约束，因此改变了轨道的模态特征。通过Simpack的Eigenvalues(onlines)特征根分析，对比钢弹簧浮置板柔性轨道的模态振型与普通刚性轨道的模态振型，发现新增164Hz、157Hz、158Hz等新的频率及相应的模态振型。

3.1 车辆钢轨耦合下的一阶典型模态分析

各部分的材料属性如表1所示。

3.2 车辆钢轨耦合下的二阶典型模态分析

164.3Hz频率为钢轨二阶弯曲和轮对点头耦合频率，如图4所示。左右钢轨的弯曲振型为二阶，而前后轮对呈现出值得关注的点头运动特征，在普通钢轨模型中并没有这一模态。该频率与上述157.4Hz钢轨一阶弯曲和轮对反向侧滚耦合频率均是引入钢弹簧浮置板柔性轨道后模态新增的频率，因此164.3Hz对应的这一耦合频率值得关注。

3.3 车辆钢轨耦合下的三阶典型模态分析

这一节是钢轨自身的三阶模态弯曲振型频率，同样是引入钢弹簧浮置板柔性模型后新增的，左轨道的三阶弯曲频率为158.8Hz，而右轨道的三阶弯曲为157.6Hz。轨道的模态振型未与车辆发生耦合，此模态振型较小，但阻尼系数也较小，如图5所示。

由上述的模态对比分析可见引入钢弹簧浮置板柔性轨道后，整个系统会产生新的模态振型，157.4Hz频率为钢轨一阶弯曲和轮对反向侧滚耦合频率，164.3Hz频率为钢轨二阶弯曲和轮对点头耦合频率，158.8Hz钢轨自身的三阶模态弯曲振型频率。这些频率与轮对点头及轮对侧滚频率相关，是轨道车辆设计中需要重点关注的模态振型。