河北省强降水对道桥影响的致灾阈值研究
2022-09-19孙玉龙王丽荣魏铁鑫
孙玉龙, 王丽荣, 张 琪, 李 婷, 魏铁鑫
(1.河北省气象灾害防御和环境气象中心,石家庄 050021; 2.河北省气象与生态环境重点实验室,石家庄 050021;3.南京信息工程大学应用气象学院,南京 210044)
引 言
在全球气候变暖的背景下,世界各地极端天气频发,气象灾害造成的经济损失也越来越大[1-3]。河北省东临渤海,西依太行山,北靠蒙古高原,南部为华北大平原,地形、地貌和气候类型复杂多样,属于气象灾害多发省份[4-6]。河北省地处季风气候区,夏季降水集中[7-8];境内有7大水系,河道上宽下窄,行洪能力上大下小,极易引发洪涝灾害[9-10]。2016年7月19-21日,河北省出现了自“63·8”极端降水以来的最强降水过程。据交通部门统计,此次降水过程共造成河北省7343 km公路、940座桥梁、2761道涵洞受损,其中,高速公路损毁145 km,普通干线损毁895 km,农村公路损毁最为严重,达6303 km,1435个村庄交通中断,直接经济损失约55.0亿元[11]。准确及时的预警预报是降低损失的主要手段。因此,有必要以道路、桥涵为承灾体,开展降水致灾指标的阈值研究,为针对重点承灾体的精细化预报服务提供科学依据。
国内已有一些关于降水致灾阈值和对道路影响方面的研究。贺芳芳等[12]采用SCS-CN 模型,通过对城市降雨径流过程的模拟,确定上海地区短历时强降水致灾阈值。郭广芬等[13]采用耿贝尔极值Ⅰ型分布和百分位方法,确定湖北省强降水引发的洪涝各等级的阈值。史军等[14]利用时空过程分析法,研究了强降水积水与降水强度及累积雨量的关系,建立了上海市中心城区内涝的阈值指标。杨勇等[15]综合应用累积分布函数值、百分位,以及标准差等方法,计算了西藏各站点的降水指标。在道路方面,狄靖月等[16]利用2007年1月-2013年7月区域(云、贵、川、渝4个地区)公路损毁灾害数据、基础地理信息数据及国家气象中心降水量历史资料,综合公路损毁灾害风险区划信息与降水的等级临界阈值,建立区域公路损毁的危险性分级预警方案。刘华斌[17]基于公路交通行业的视角,运用灾害学、多元统计学、计量经济学等方法评估了强降水造成的城市内涝灾害经济损失。贾剑波等[18]对2011年和2012年北京2场强降水期间高速公路边坡26处滑坡进行实地调查,同时分析出现边坡滑坡的原因和发生机制。以往的研究中,大多只考虑了降水自身的特点,而对重点承灾体的阈值研究较少,且很少结合历史灾情数据进行分析。
河北省是首都北京连接全国各地的必经之地,具有道路长度长、桥涵数量多的特点,强降水引发的洪水和内涝易导致道路损毁、桥梁坍塌、交通中断,严重影响人民的生产生活,并造成严重的经济损失[11,19]。目前,从预报预警角度出发,专门针对河北省道桥这一重要影响对象开展的降水致灾阈值研究很少。本研究以道桥为承灾体,利用河北省1984-2014年逐日降水资料和历史灾情案例,采用最优分割法[20],将历史灾情划分为四个等级,基于逻辑回归法[21]确定不同灾情等级的降水致灾指标的阈值,并对阈值应用效果进行检验,以期为河北省降水的精细化预警预报服务提供技术支撑。
1 研究区概况
河北省位于中纬度欧亚大陆东岸、华北区域中心,地势呈现西高东低势态(图1),地形地貌复杂多样,高原、山地、丘陵、盆地、平原类型齐全,气候类型表现为暖温带半湿润半干旱大陆性季风气候,一年中干湿期明显,夏季炎热潮湿,冷暖空气交绥剧烈,降水集中,夏季降水量占全年总降水量的70%左右,降水集中的时段易发生严重的洪涝灾害[22]。此外,夏季易受到东北低压、蒙古低涡、冷锋、台风等影响[23]。交通方面,河北省地处华北、环抱北京,交通网密集,全省共有27条国家干线公路,公路货物周转量居全国大陆省份第2位;全省高速公路通车总里程达到7279 km,居全国第二位[19]。

图1 河北省地形及国家标准气象站分布图
2 资料与方法
2.1 数据来源
本研究以县为研究单元,降水数据为河北省1984-2014年142个国家地面气象观测站(图1)的观测资料,来自河北省气象局。道桥由于极端降水造成损失的灾情数据来自河北省各市档案局、救灾办、水利局、气象局、民政厅等部门,以及《中国气象灾害大典(河北卷)》、报表文件等文献资料,经过进一步数据控制(逐条核对、审查剔除异常和重复的灾情记录),构建强降水导致道桥损失的灾情案例库,共计216个案例。
2.2 道桥损失数据校正
2.2.1 年代校正
由于不同年代桥涵、道路的建造质量不同,同样强度的降水发生在不同的年代带来的灾害损失会有所不同,因此需要对道桥损失数据进行年代校正,以消除不同年代桥涵自身脆弱性差异对灾情损失数据的影响。
根据历史灾情数据计算各个时期(每5年为一个时期,第一时期为6年)所有灾情案例的道路损失长度的平均值和灾情案例对应的5日累积降水量的平均值,计算各个时期造成单位长度道路损失所需要的累积雨量,所需累积雨量越高,说明该时段内道路的平均质量越高,不易成灾。将2010-2014年作为基准时期,各个时期的单位损失雨量与基准时期的比值作为校正系数,将道路损失长度乘以年代校正系数即为折合成相当于2010-2014年的道路质量水平下的损失长度(表 1)。例如,1995-1999年损失单位长度道路所需的累积雨量仅为0.64 mm,该时段道路脆弱性较大,易成灾,对应的校正系数为0.37,将原实际道路损失长度乘以该校正系数,则得到校正到2010-2014年道路脆弱性水平下的损失长度,校正后损失长度有所减少。
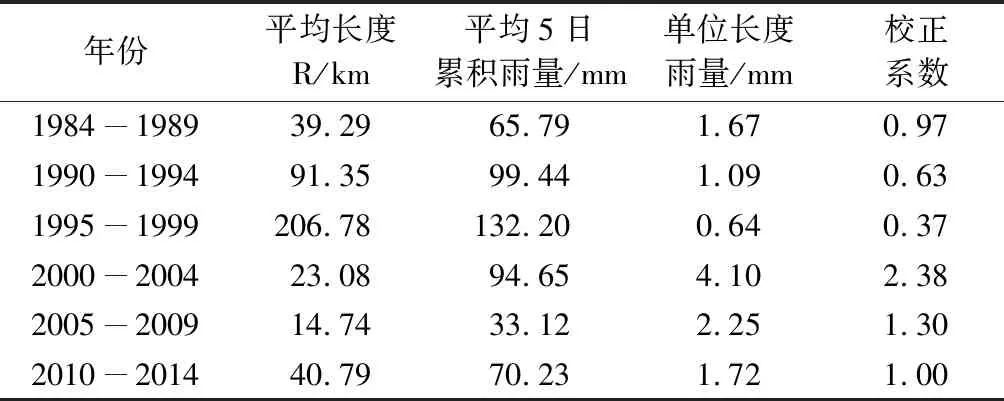
表1 1984-2014年河北省道路损失年代校正系数
桥涵损失的年代校正系数计算过程与道路的相同(表2)。道路损失长度(桥涵损失个数)年代校正前后与5日累积降水的相关系数由0.184(0.341)提高到0.203(0.394),都通过了0.01的显著性检验。
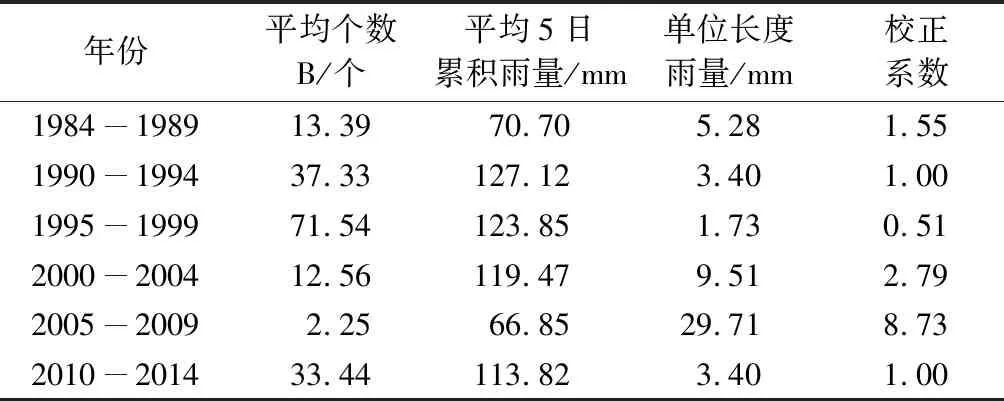
表2 1984-2014年河北省桥涵损失年代校正系数
2.2.2 面积校正
由于灾情数据以县为单位进行统计,县的面积的大小一定程度上会影响灾情的大小,因此将经过年代校正的灾情数据与县域面积的比值(单位面积灾损数据)作为后续灾情等级划分依据。道路(桥梁)损失数据单位面积处理前后与5日累积降水的相关系数由0.203(0.394)提高到0.218(0.498),均通过了0.01的显著性检验。因此本研究统一采用经过面积校正后的数据。
2.3 基于最优分割法的灾情等级划分
Fisher在1958年最先提出最优分割方法,在保证不破坏原有样本的前提下,以分组后组内离差平方和最小不同组间离差平方和最大为原则,对有序样本或可变为有序的样本进行分级的一种聚类分级方法[20],在干旱、洪涝等自然灾害等级划分、汛期分期、地震分期等方面具有较多的应用。最优分割法较常用的成因分析法、数理统计法等在分类确定等级时能够较少地受到主观因素的影响。
基于最优分割法分别将道路和桥涵灾情案例划分为轻、中、重、特重四个等级(表3),最终的道桥综合灾情等级按照道路、桥梁双指标就高的原则划定。将5日累积降水与桥梁灾情等级、道路灾情等级、综合灾情等级进行相关分析,相关系数分别为0.467、0.240、0.550,都通过了0.01的显著性检验。综合后的灾情等级明显优于道路和桥梁独自的情况。

表3 道桥灾情等级划分标准
2.4 逻辑回归法
回归分析是研究变量之间函数关系的一种方法。在实际问题中,有时因变量为定性量、自变量为随机量,不符合多元线性回归的假定。例如,在强降水事件中,过程累积降水量、降水日数、最大小时雨强等多为随机变量,而更应关注的预测结果是会不会成灾,是一个[0,1]二项分布的问题。
针对这一问题,利用Logistic 回归模型预测不同等级的灾害。Logistic函数是一种基于统计学和确定性模型相结合的分析方法,并被广泛应用于自然科学、社会科学、管理科学和经济学等领域。逻辑回归的本质是进行二分类,其方程式为
(1)
式(1)中,P为事件发生的概率,x为自变量,β为回归方程的系数。
利用统计资料,通过式(1) 回归分析给出回归系数,再对式(1)进行指数转换,可得式(2),即条件概率预测模型:
(2)
式(2)中,y=β0+β1x1+β2x2+…+βkxk。
逻辑回归模型是一种统计学模型,其自变量可以是连续的,也可以是离散的,且不必满足正态分布;同时,在用该模型进行计算时,不会出现P>1或P<0的不合理情况。逻辑回归模型的计算结果具有较强的客观性和稳定性。一般情况下以P=0.5为界线,当P>0.5定义为事件发生;P<0.5定义为事件不发生。
在当前暴雨灾害致灾指标阈值的研究中,最常用的方法是综合指数法,将各个关键致灾因子按照重要程度采用某种数学公式计算出一个综合的指标。该类方法的优点是可以把相关的致灾指标都考虑进来,但主要问题是这个综合指标的数值缺乏实际的物理意义,如果不查看原始数据,并不能直观看到某次灾情事件具体是由暴雨哪个方面的特征造成的。
因此,本研究采用逻辑回归的方法,将降水致灾指标直接与灾情等级建立关系,确定不同等级灾情对应的降水指标的取值范围,阈值划分结果更加直观,每个指标都有明确的物理含义。
2.5 降水致灾指标的筛选
河北省的道桥损毁灾害大部分是由于强降水诱发的滑坡、泥石流、洪水冲刷等造成的。强降水致灾与降水总量、集中程度、持续时间等有最直接的关系[24-26]。综合考虑灾情案例的降水特征后,将5日累积降水量作为描述灾情过程的降水总量多寡的指标,以对应的大雨日数为描述降水集中程度的指标,将连续降水日数作为表述持续时间的指标。
将综合灾害等级与各个指标进行相关分析(表4)可以看出,综合灾情等级与各致灾指标的相关性较好,通过了0.01的显著性检验。由于连续日数与综合灾情等级的相关系数偏低,5日累积降水量已经考虑了持续时间的因素,再加上2.4中的逻辑回归法不宜考虑过多的指标,指标过多会造成不同指标的不同等级组合数量成倍增长,增加了指标的复杂性,因此,最终考虑将5日累积降水量和对应的大雨日数确定为强降水对道桥影响的致灾指标。

表4 所选指标与综合灾情等级的相关系数
3 结果与分析
3.1 不同灾情等级致灾指标的阈值
基于逻辑回归法,以5日累积降水量和对应的大雨日数作为致灾因子指标,进行不同灾情等级致灾阈值的划分。将灾情等级作为因变量Y,5日累积降水量和大雨日数作为自变量X1、X2,采用逻辑回归法确定不同等级灾情之间的分割线(图2)。图中不同形状的符号代表不同等级的历史灾情案例,不同形式的直线为相邻两个灾情等级之间的分割线,实线为特重和重度等级的分割线,长虚线为重度和中度等级的分割线,短虚线为中度和轻度等级的分割线。根据3条分割线,可得到不同大雨日数对应的5日累积降水量阈值。
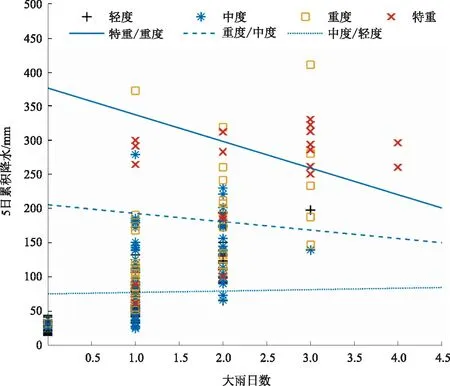
图2 基于逻辑回归法确定的不同等级灾情分界线图
表5为各个灾情等级对应的致灾阈值。当大雨日数为0天时,轻度灾情等级的5日累积降水量阈值为16.7 mm;当大雨日数为1天时,轻度、中度、重度、特重四个灾情等级的5日累积降水量阈值分别为37.8 mm、80.0 mm、190.0 mm、338.4 mm;当大雨日数为2天时,四个灾情等级的5日累积降水量阈值分别为58.9 mm、81.8 mm、184.0 mm、300.4 mm;当大雨日数为3天时,中度、重度、特重灾情等级的5日累积降水量阈值分别为84.8 mm、171.8 mm、262.5 mm;当大雨日数为4天时,重度、特重灾情等级的5日累积降水量阈值分别为160.5 mm、224.6 mm。

表5 不同灾情等级对应的大雨日数和5日累积降水量阈值 mm
3.2 基于致灾阈值的灾情预测等级分析
基于表5中的致灾阈值,根据每个历史灾情案例的5日累积降水量和大雨日数,反推对应的灾情预测等级,统计每个预测等级的案例个数,并与实际等级的案例个数进行对比分析。例如,所有案例中共有13个案例的预测等级为特重,这13个案例实际的灾情等级情况为9个特重、4个重度(表6)。当某个灾情案例的预测等级和实际等级一致时,则判定基于致灾阈值对该案例的预测准确,由此可计算出各个灾情等级的准确率(图3)。

表6 基于致灾阈值的历史灾情等级划分结果
3.2.1 所有灾情案例的准确率
216个灾情案例中,预测为各个等级的案例中都是实际为该等级的案例所占比例最高,不同等级之间特重灾情和轻度灾情的准确率较高,分别为69.2%和67.3%(图3),四个等级平均准确率为56.7%。若计算准确率时将下一等级一起统计,准确率会有大幅提高,特重灾情达到100%,四个等级平均准确率为76.4%。
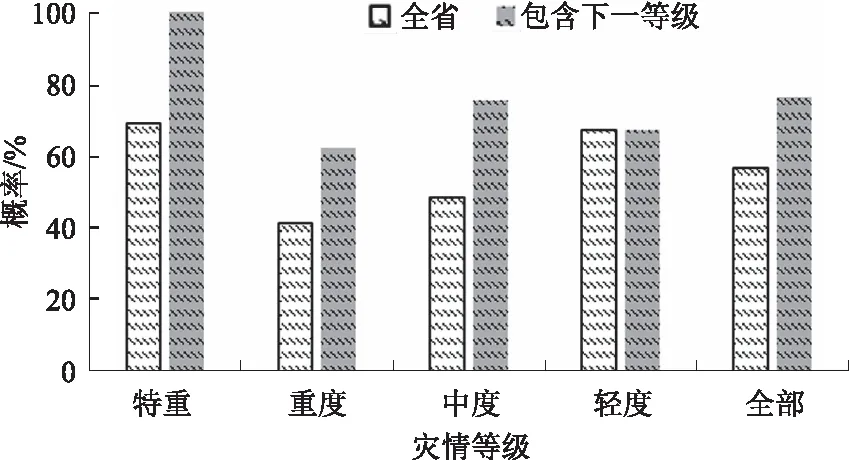
图3 不同区域各个等级灾情判定准确率
3.2.2 山区和平原灾情案例的准确率
根据地形,将山区(153个)和平原(63个)灾情案例分开统计准确率,结果表明,山区案例不同等级之间特重灾情和轻度灾情的预测准确率较高,分别为83.3%和70.5%;平原案例不同等级之间特重灾情和中度灾情的预测准确率较高,分别为57.1%和53.3%(图4)。相比之下,山区案例的预测准确率明显高于平原的准确率,山区和平原四个等级的平均预测准确率分别为65.8%和44.9%;若将邻近的下一等级考虑进去,预测准确率分别为80.6%和67.5%。由此可见,山区道桥损坏对强降水的敏感程度要高于平原地区的敏感度,有更好的评估效果。
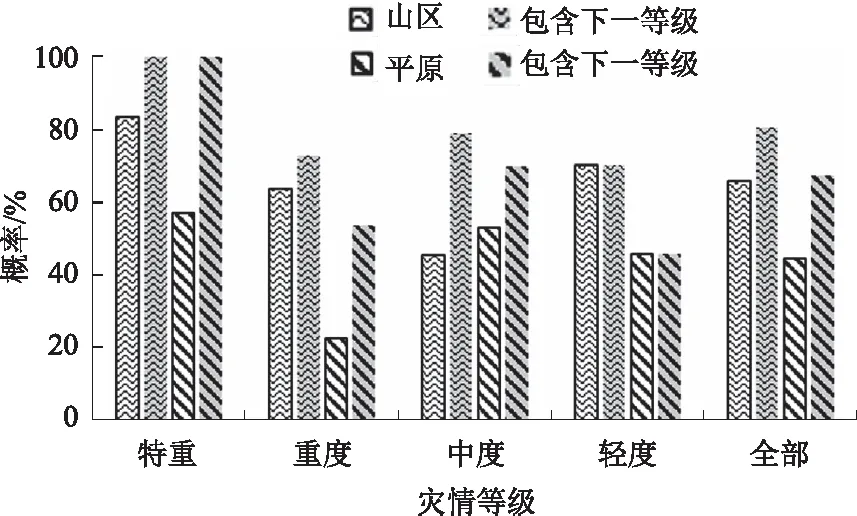
图4 山区和平原各个等级灾情判定准确率
3.2.3 不同大雨日数案例的准确率
基于致灾阈值,对不同大雨日数灾情案例的准确率(表7)进行统计分析:大雨日数为0天的案例有39个,均预测为轻度灾情,其中79.5%的案例实际灾情等级也为轻度,预测准确率高;大雨日数为3和4天时以重度和特重灾情为主,平均准确率也较高,分别为60.0%和100.0%,其中大雨日数为3天的8个特重等级案例中有6个预测准确,准确率为75%;大雨日数为1天时,主要灾情类型为轻度灾情和中度灾情,整体准确率偏低。结合图2可以看到,较多的样本实际等级比预测等级高一个等级,因此大雨日数为1天时累积雨量的阈值偏高,可考虑参考其他致灾因子进行修正。

表7 基于致灾阈值的不同大雨日数案例的个数及准确率
4 结论与讨论
本文以道桥为承灾体,采用最优分割法将历史灾情划分为轻、中、重、特重四个等级,以5日累积降水量和大雨日数为致灾指标,基于逻辑回归法计算出各个等级的降水指标致灾阈值,得到以下结论:
(1)当大雨日数为1天时,轻度、中度、重度、特重四个灾情等级的5日累积降水量阈值分别为37.8、80.0、190.0、338.4 mm;当大雨日数为2天时,四个灾情等级的5日累积降水量阈值分别为58.9、81.8、184.0、300.4 mm;当大雨日数为3天时,中度、重度、特重灾情等级的5日累积降水量阈值分别为84.8、171.8、262.5 mm;当大雨日数为4天时,重度、特重灾情等级的5日累积降水量阈值分别为160.5、224.6 mm。
(2)所有灾情案例中,预测为各个等级的案例中都是实际为该等级的案例所占比例最高,不同等级之间特重灾情和轻度灾情的准确率较高,分别为69.2%和67.3%。山区案例的准确率明显高于平原,山区和平原四个等级的平均准确率分别为65.8%和44.9%,山区道桥损坏对强降水的敏感程度要高于平原地区的敏感度,有更好的评估效果。
(3)对于不同大雨日数的灾情案例,0天和3天及以上的大雨日数的灾情等级预测准确率高,大雨日数为1~2天时准确率整体偏低,预报难度较大,将在今后的研究中参考其他致灾因子进行修正。
(4)本研究采用逻辑回归的方法将降水致灾指标直接与灾情等级建立关系,确定不同等级灾情对应的降水指标的取值范围,阈值划分结果更加直观,每个指标都有明确的物理含义。但该方法不宜考虑过多的指标,指标过多会造成不同指标的不同等级组合数量成倍增长,增加了指标的复杂性。因此在今后的研究中,可采用综合指数法进行对比研究。
