空间七自由度机械臂动力学建模与仿真
2022-09-19侯月阳夏泽群董洋洋张子建
邱 雪,钟 超,侯月阳,夏泽群,董洋洋,张子建
(1.南京航空航天大学航天学院,江苏 南京 210016)(2.上海航天控制技术研究所,上海 200233)
随着空间技术的高速发展,特别是空间站、航天飞机等的诞生及成功应用,空间机械臂作为完成目标捕获、在轨组装与服务、星表样本采集等任务的关键装备发挥着越来越重要的作用[1-2]。空间七自由度机械臂相比非冗余机械臂其操作灵活性大为提高,在各国航天领域受到越来越广泛的关注[3]。但针对七自由度机械臂的动力学建模更加复杂,且计算量较大,难以应用于机械臂系统的实时控制与仿真。
动力学模型是空间机械臂规划与控制的基础,建立正确、高效的动力学方程对于设计高性能控制器及机械臂系统仿真等具有重要意义,国内外许多学者在机械臂动力学建模与控制方面做了大量研究工作。目前,机械臂动力学建模方法主要有以牛顿-欧拉法为代表的矢量力学方法[4-6]、以拉格朗日方法为代表的分析力学方法[7-9]以及兼具矢量力学和分析力学特点的凯恩法[10-11],它们的计算复杂度分别为O(n3)、O(n4)和O(n2)。上述传统动力学建模方法中拉格朗日方法应用相对较多,王磊等[12]利用拉格朗日方法建立了两自由度机械臂动力学模型;刘文超[13]采用拉格朗日方法建立了三自由度机械臂动力学模型并进行轨迹跟踪控制;李鹏飞[14]采用拉格朗日方法建立了六自由度机械臂动力学模型并分析其动力学特性。这种传统的方法对于低自由度机械臂动力学建模是方便可行的,但随着系统自由度增加,方程复杂度呈指数增长,其算法计算效率低,不能满足复杂机械臂系统实时控制和仿真的需要[15-16]。因此,建立计算效率高的机械臂动力学模型成为重要研究方向之一。肖爽等[17]采用拉格朗日方法建立五自由度机械臂动力学模型并利用机械臂特殊构型对方程进行简化,最终实现了对机械臂的实时控制,不过该方法不具备普适性。
本文针对空间七自由度机械臂基座位姿固定和自由漂浮两种工作状态,研究了计算量为O(n)次的高效率动力学建模方法[18-21],推导了基于旋量和铰接体惯量理论的正向动力学模型和逆向动力学模型,并基于逆向动力学模型建立了机械臂位置控制系统,实现了机械臂实时轨迹跟踪控制。
1 动力学建模基础
为了建立能够用于机械臂实时控制和仿真的高效、简洁的动力学模型,使用空间矢量描述机械臂系统的各物理量,并引入铰接体概念[21]。对于机械臂系统,连杆(i-1)的子树即为铰接体i,以此类推,如图1所示。

图1 铰接体示意图
对本文研究的机械臂系统作如下假设:1)文中涉及的机械臂系统为刚体系统;2)机械臂与基座、相邻连杆间只有一个转动关节,关节无柔性;3)机械臂系统拓扑结构为链式,无支路且末端自由;4)空间微重力环境下忽略重力的影响。
基于上述假设,对空间七自由度机械臂正动力学建模进行研究。存在铰接体惯量定理,使得机械臂系统中的某个体受力为[19]:
(1)

首先根据机械臂连杆之间运动学量的递推关系可以得到铰接体加速度的表达式;再对空间机械臂系统中单个连杆进行受力分析,可解出关节角加速度;最后结合式(1)可得到递推形式的铰接体惯量和铰接体偏向力表达式,进而得到机械臂正向动力学模型。
2 基座位姿固定机械臂动力学建模
2.1 正向动力学
基座位姿固定情况下基座的速度和加速度均为零,利用机械臂各关节角加速度的表达式,可得到递推形式的机械臂正向动力学模型。
1)运动学量向外递推。
i=1,2,…,n循环:
(2)
2)铰接体惯量和铰接体偏向力向内递推。
i=n,n-1,…,2循环:
(3)
3)加速度向外递推计算。
i=1,2,…,n循环:
(4)

由上述模型可以得到初始时刻机械臂各关节的角加速度,为求得下一时刻各关节角度及角速度,本文采用经典的龙格库塔方法进行数值积分,最终实现了对机械臂运动状态的仿真。
2.2 逆向动力学
对于基座位姿固定的逆向动力学建模,同样已知基座速度、加速度均为零,传统的牛顿-欧拉建模方法重复运算多,计算效率不高,采用旋量代替三维向量描述各运动学和力学物理量,克服了上述缺点,提高了计算效率。
1)运动学量向外递推。
i=1,2,…,n循环:
(5)
2)力学量向内递推。
i=n,n-1,…,1循环:
(6)
由以上逆向动力学模型,根据机械臂运动状态,可快速地求解出各关节驱动力矩,用于固定基座机械臂的实时控制。
3 基座自由漂浮机械臂动力学建模
3.1 正向动力学
与基座位姿固定的动力学建模不同,漂浮基座的速度与加速度不为零,可以看成是基座通过6-DOF的虚拟铰链与惯性坐标系连接。因此,机械臂系统自由度大大增加,使得动力学建模更加困难,模型更加复杂。本文在固定基座正向动力学模型的基础上进一步扩展,得到了漂浮基座的正向动力学模型。
对于基座自由漂浮的空间机械臂,将整个系统视为铰接体0,由于铰接体0不受外力作用,因此有:
(7)
(8)
(9)

1)运动学量向外递推。
i=1,2,…,n循环:
(10)
2)铰接体惯量和铰接体偏向力向内递推。
i=n,n-1,…,2循环:
(11)
3)加速度向外递推计算。
i=1,2,…,n循环:
(12)
3.2 逆向动力学
逆向动力学模型是根据机械臂运动状态求解各关节驱动力矩。对于基座自由漂浮的空间机械臂,各关节加速度已知,但基座的加速度未知,因此求解该逆向动力学模型是一个动力学混合问题。基座自由漂浮的空间机械臂系统不受外力作用,系统的动量守恒,结合动量守恒定理对固定基座机械臂的逆向动力学算法进行改进,得到了基座自由漂浮的机械臂逆向动力学模型。
1)运动学量向外递推。
i=1,2,…,n循环:
(13)
2)组合体惯量和组合体偏向力向内递推。
i=n,n-1,…,1循环:
(14)
3)关节力矩向外递推。
i=1,2,…,n循环:
(15)

根据已知的机械臂运动状态及基座初始运动状态,运用上述基座自由漂浮的空间机械臂逆向动力学算法,可以得到机械臂各关节需要的驱动力矩及机械臂运动对基座产生的扰动力和力矩,进而判断机械臂运动对基座载体产生的影响,为任务规划提供依据。
4 仿真试验及结果分析
利用MATLAB编写空间七自由度机械臂正、逆动力学算法(简称ABA),并在SimMechanics中建立该机械臂物理模型,比较二者之间的仿真结果。仿真步长设置为0.01 s,仿真时间为10 s。空间七自由度机械臂及其固连坐标系如图2所示。
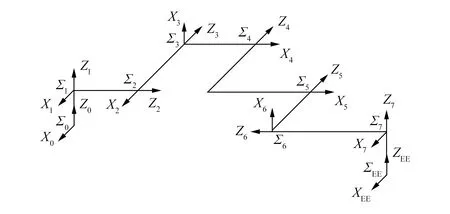
图2 空间机械臂固连坐标系
机械臂质量、固连坐标系原点位置、连杆质心位置、转动惯量等动力学参数见表1。其中,坐标系原点位置是相对于上一级连杆固连坐标系,连杆质心位置是相对于本级连杆固连坐标系,另外惯性系与基座本体系初始位姿相同。
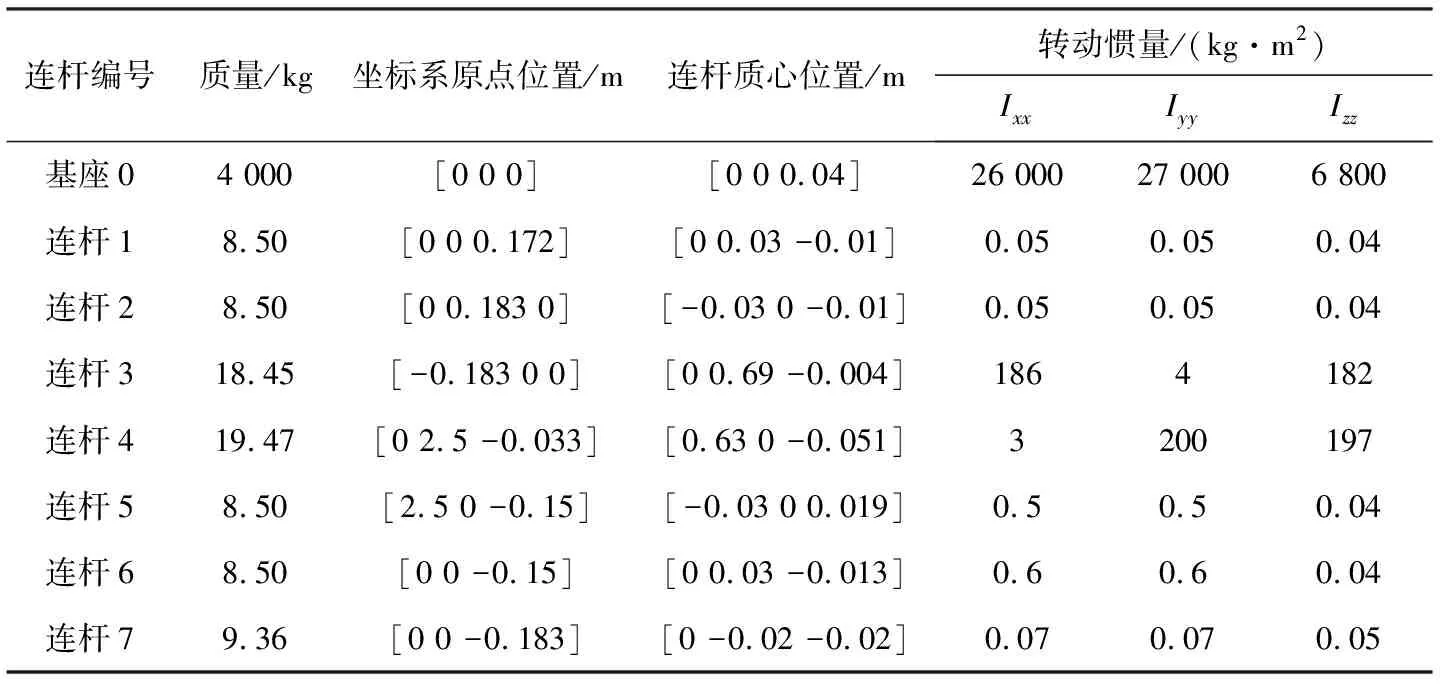
表1 空间机械臂动力学参数
4.1 基座位姿固定机械臂动力学仿真
假设机械臂各关节驱动力矩为sint、0.3cost、0.3sint、0.2cost、0.2sint、0.03sint、0.02sintN·m,由正动力学模型可以计算得到机械臂各关节运动情况。基座位姿固定情况下的仿真结果如图3、图4所示。
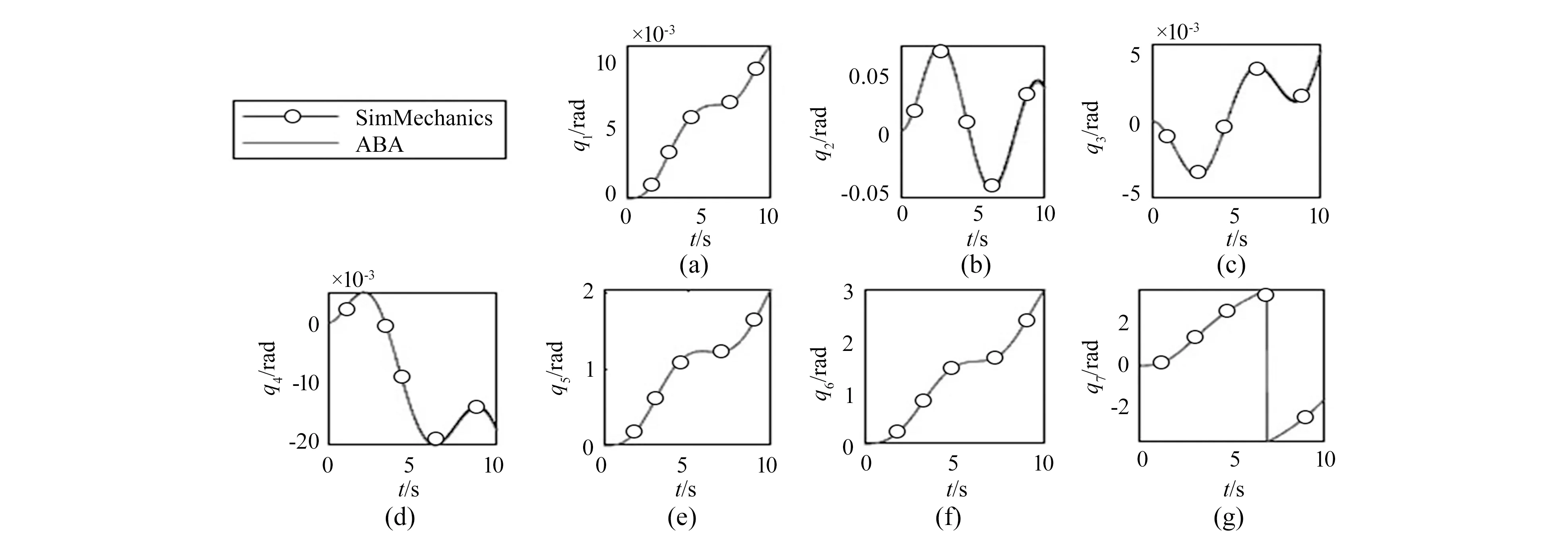
图3 基座位姿固定机械臂各关节角度曲线

图4 空间机械臂各关节角速度曲线
假设机械臂各关节角度变化曲线均为0.1costrad,通过逆动力学模型可以计算得到各关节所需的驱动力矩。基座位姿固定情况下机械臂各关节驱动力矩仿真曲线如图5所示。
由图3和图4可以看出,正动力学算法仿真得到的机械臂各关节的角度、角速度曲线与SimMechanics得到的一致;由图5可以看出,逆动力学算法得到的机械臂各关节驱动力矩曲线与SimMechanics得到的一致。由此,可以验证基座位姿固定情况下空间机械臂动力学模型算法的准确性。
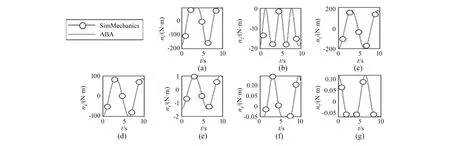
图5 空间机械臂各关节力矩曲线
4.2 基座自由漂浮机械臂动力学仿真
假设机械臂各关节驱动力矩为cost、0.5sint、0.5cost、0.1sint、0.1cost、0.05cost、0.01costN·m,由正动力学模型可以计算得到机械臂各关节运动情况及基座位姿扰动。基座自由漂浮情况下机械臂各关节角度曲线如图6所示,基座位姿扰动曲线如图7所示。
假设空间七自由度机械臂各关节角度变化曲线均为0.1sintrad,通过逆动力学模型可以计算得到各关节所需的驱动力矩及基座受到的扰动力。基座扰动力曲线如图8所示。
由图6和图7可以看出,正动力学算法仿真得到的机械臂各关节的角度和基座位姿扰动曲线与SimMechanics得到的一致;由图8可以看出,逆动力学算法得到的机械臂基座扰动力曲线与SimMechanics得到的一致。由此,可以验证基座自由漂浮情况下空间机械臂动力学模型算法的准确性。

图6 基座自由漂浮机械臂各关节角度曲线
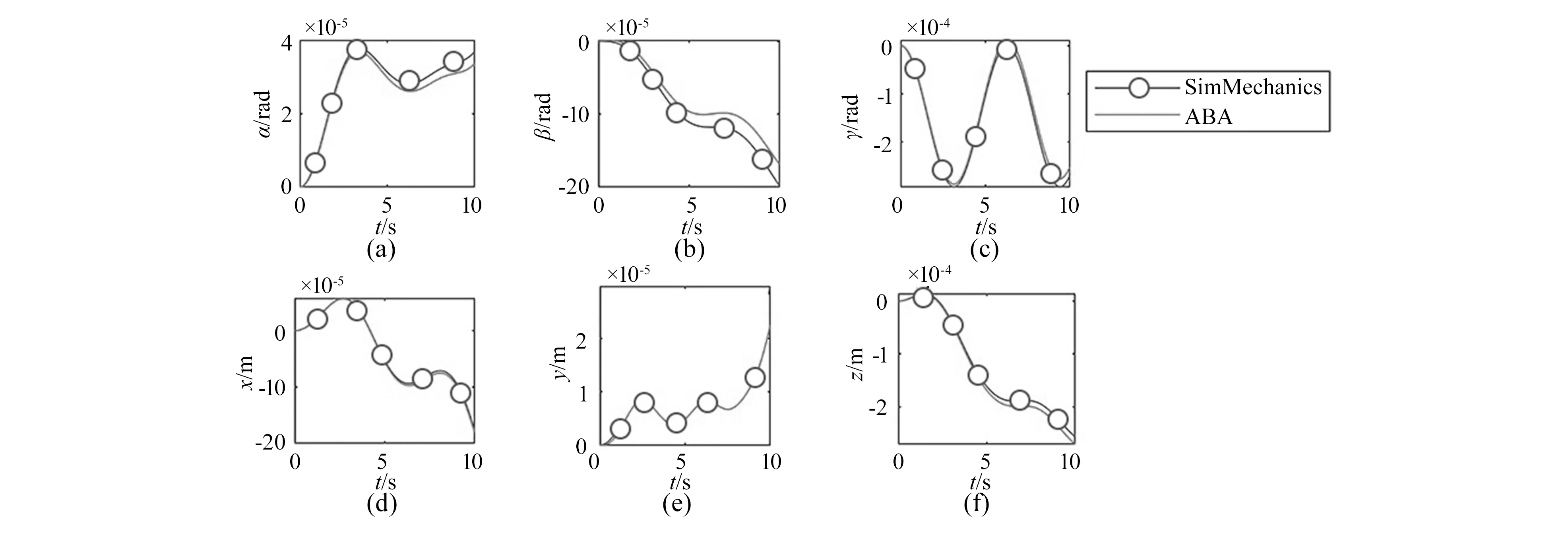
图7 基座位姿扰动

图8 基座扰动力
4.3 基于逆动力学模型的位置控制仿真
为证明本文建立的动力学算法具有计算量小、计算效率高、可用于机械臂实时控制等优点,基于上述逆动力学模型设计了位置控制器,实现了空间七自由度机械臂对期望轨迹的实时跟踪控制。控制框图如图9所示。
位置控制器的基本设计思路为利用逆动力学模型在内控制回路中引入非线性补偿,将机械臂化为一个更容易控制的线性定常系统。控制律的完整表达式如下:
(16)
为验证基于逆动力学算法的位置控制器的控制效果,假定机械臂各关节的期望关节角度分别为sint、cost、0.5sint、0.5cost、sint、cost、0.5sintrad,对控制系统进行仿真得到关节轨迹跟踪误差,误差曲线如图10所示。
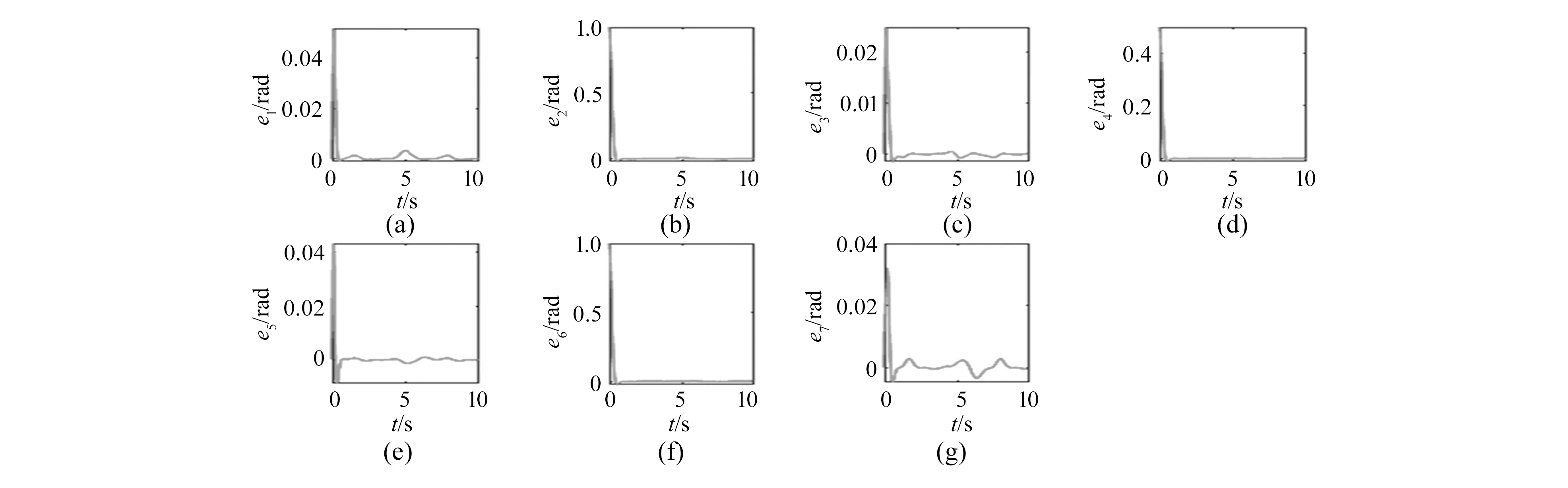
图10 空间机械臂各关节角度跟踪误差曲线
由图10 可以看出,尽管期望关节角度幅值比较大、变化较快,但控制器仍能够很好地跟踪期望关节角度,可以证明本文建立的基于逆动力学的位置控制器动态性能良好,进而表明本文推导的动力学算法能够应用于七自由度机械臂的实时控制与仿真。
5 结束语
本文针对空间七自由度机械臂基座位姿固定和基座自由漂浮两种情况,建立了基于空间矢量和铰接体惯量的机械臂正、逆动力学模型,并将上述逆动力学模型应用于位置控制器,得到了很好的控制效果。本文研究的动力学建模方法扩展性强,可以应用于空间机械臂与被抓捕物体的组合体建模、闭环系统建模及基座自由飞行情况下的动力学建模。
