数控插齿机热误差模块化稳健性预测模型建立

李淋，蔡站文，杨勇，李建刚

(1.重庆理工大学机械工程学院，重庆 400054；2.哈尔滨工业大学机电工程与自动化学院，广东深圳 518055)

0 前言

随着机床设计与制造技术日趋成熟与完善，热误差已经成为数控加工设备最大误差源，制约其加工精度的进一步提升。因此，近年来数控加工设备的热误差建模理论逐渐成为国内外研究的热点。周宝仓、DAI等针对大型数控磨齿机，通过建立磨齿机热误差试验平台，研究砂轮与工件轴的径向热误差随温度变化的关系，揭示成形磨齿机热误差与温度之间的关系。YANG、LIU等针对干式滚齿机的热变形误差特征，利用灰狼优化算法和神经网络建立了误差补偿模型，泛化性良好。苗恩铭、WEI、LIU等采用多种算法建立了Leaderway V-450数控加工中心关键点的温度和主轴向的热变形量预测模型，大幅提升了热误差稳健性。目前，国内外对数控插齿机的研究主要集中在几何误差和回转误差，并取得了较好的成果和发展，然而，对数控插齿机床进行热误差建模的研究却很少。为此，本文作者以YKS5132DX3型数控插齿机为试验对象，研究其热误差规律及建模方法。

基于数控插齿机固有的主轴进给系统结构带来的传动间隙，在加工齿轮的过程中随着温度的上升间隙增大，进而产生波动性的热变形，提出一种热误差模块化建模方法。因特性曲线不同，对于传统的热误差曲线，综合应用常规的模糊聚类与灰色关联度理论进行温度敏感点的选择，同时利用多元线性回归模型建立热误差补偿模型。对于模块化建模方法，选取均值平滑法处理热误差曲线；与传统的建模方法进行比对，验证所提建模方法的稳健性。

1 温度敏感点的选择理论及回归模型

热误差建模包括温度敏感点的选择和建模算法两项关键理论。温度敏感点即热误差模型的输入变量，对提升模型的预测精度和稳健性起着决定性作用。为减小温度敏感点之间的共线性和提升温度敏感点与热误差之间的关联性，依据传统的模糊聚类结合灰色关联度的敏感点优化方法，对试验数据进行温度敏感点的筛选及分析，并运用多元线性回归算法建立热误差与温度敏感点之间的函数关系。

1.1 温度敏感点优化方法

(1)模糊聚类

①采用相关系数法建立温度测点模糊聚类相似矩阵=[]×，,=1,2,…,(为温度测量点数)，表示第个和第个温度测点之间的相关系数，计算公式为

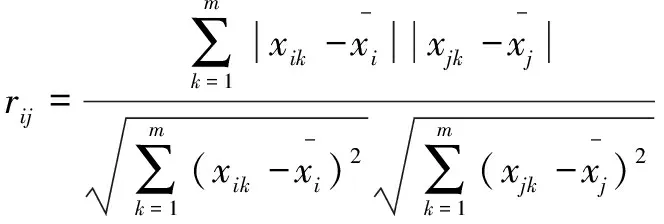
(1)

式中：为离散的测量时间点；为试验数据长度。

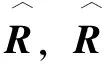
→→()→…→2

(2)

(2)灰色关联度

在系统发展过程中，如果两个因素变化的态势是一致的，即同步变化程度较高，则可以认为两者关联度较大；反之，则两者关联度较小。文中采用邓氏关联度计算公式，即:

(3)

式中：代表热误差；代表第个温度测点观测值；()、()分别代表热误差和第个温度测点的第个观测值；(,)为热误差和第个温度测点之间的灰色关联度，由各个观测值的关联度[(),()]求平均值而来。[(),()]计算公式如下：

[(),()]=

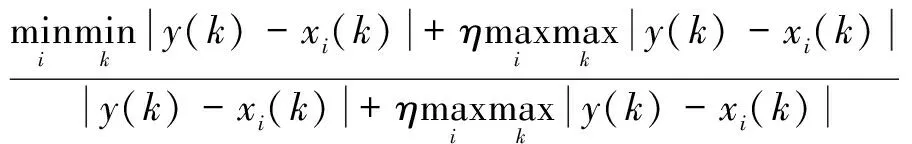
(4)

式中:为分辨系数，∈[0，1]，一般取=0.5。

根据以上公式计算出数控机床热误差与各个温度点数据之间的关联度。关联度越大，说明该温度点变化趋势和热误差相似程度较大。选用每类中关联度最大的传感器作为温度敏感点参与热误差建模。

根据模糊聚类结合灰色关联度相结合的方法，最终确定、轴两个方向热误差对应的温度敏感点分别为、，、。

1.2 多元线性回归模型

多元线性回归是研究一个因变量与多个自变量之间相关关系的模型，在工程应用中被国内外学者大量使用，也是数控机床热误差补偿控制技术中常使用的预测模型建模方法。根据机床的热误差实际情况，建立以多个关键温度敏感点测量的温度增量为自变量，以热变形量为因变量的热误差模型，其通用公式为

=+1+2+…++

=1,2,…,

(5)

式中:(1,2,…,)为关键温度敏感点温度测量增量值;(，，…，)为温度变量的系数;为热变形量;为与实际测量值存在的偏差，也称残差。

2 数控插齿机床热误差试验设计

2.1 试验方案

为避免错过温度敏感点，温度传感器应尽量布置在热源附近且尽可能多地布置。为此采用热像仪对数控插齿机的工作温度进行测量，再根据经验对插齿机可能的温度敏感点进行测量。本文作者对YKS5132DX3数控插齿机主轴、向进行热误差测量试验，各传感器的安放位置及作用如表1所示，具体分布位置如图1所示。

表1 传感器安放位置

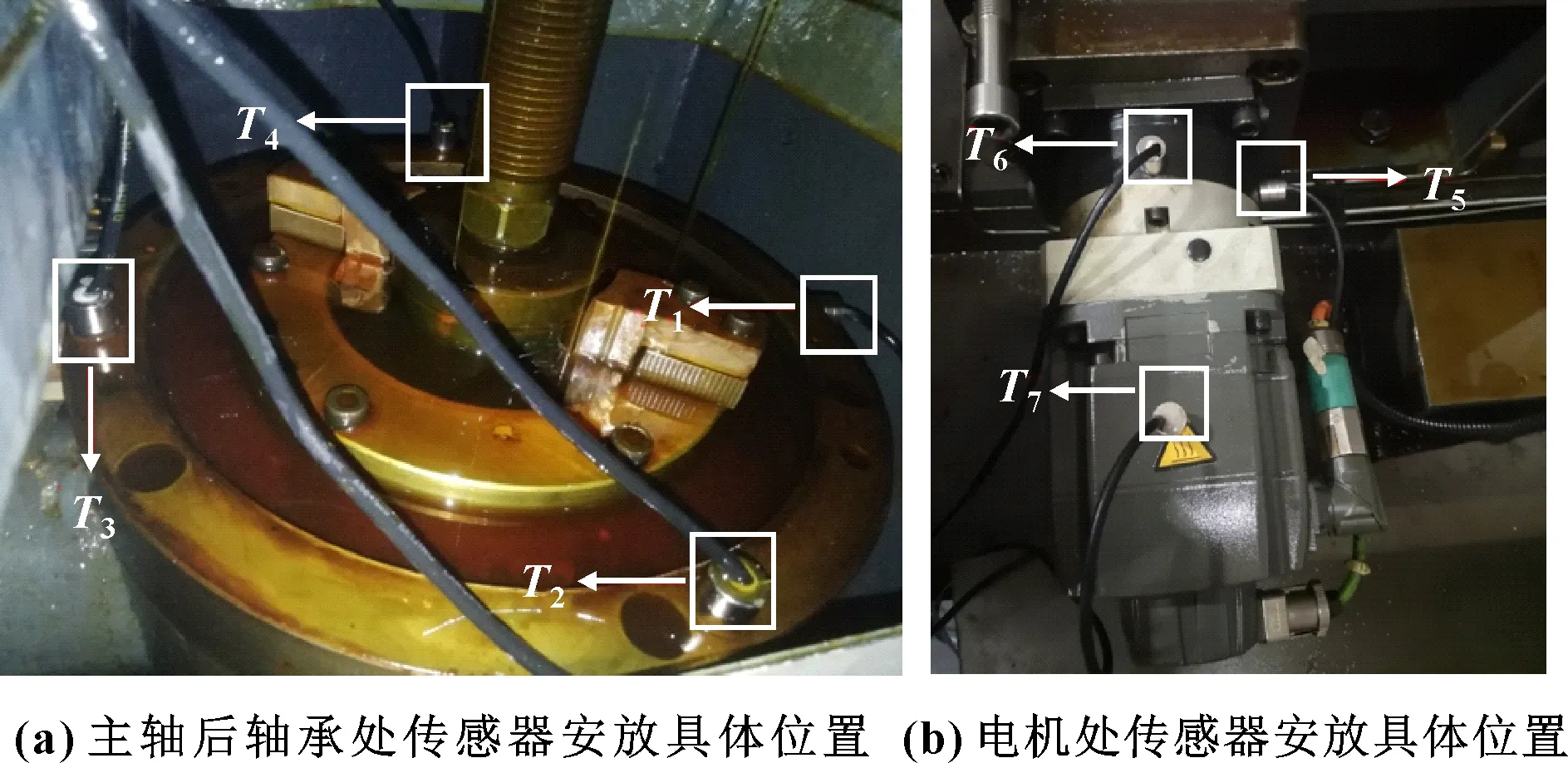
图1 传感器安放位置

2.2 试验安排

测量时，工作台转速设定为500 r/min，主轴以恒定的进给速度380 mm/min作往复运动，每完成一个循环(约3.5 min)主轴停转15 s，以测量主轴、向热误差，并通过温度测量系统采集该时刻的温度数据，测量试验持续时间均达7 h以上。

在室内无空调状况下一共进行了两批次试验，结果如表2所示，热误差曲线如图2所示。以K1批次试验数据为例，图3给出了各温度点的温度曲线。

表2 各试验批次主轴转速和环境温度

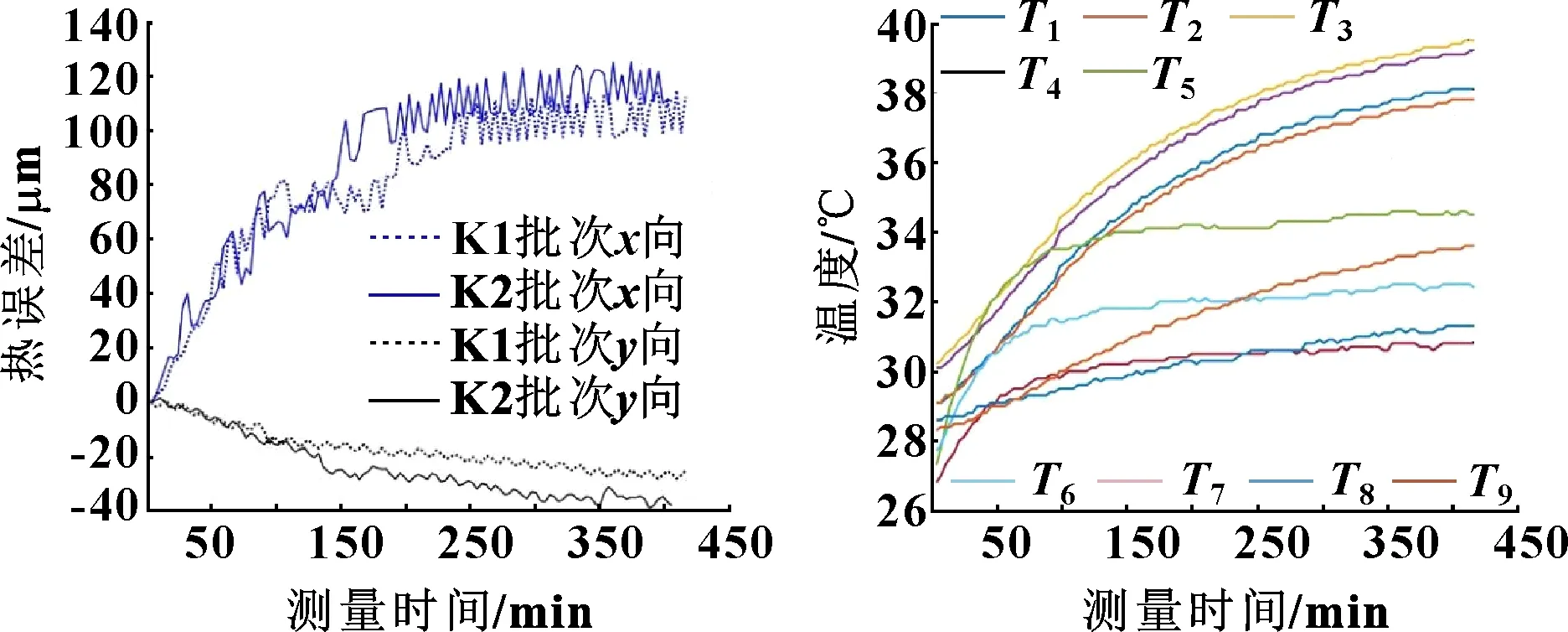
图2 K1、K2批次试验数据的热误差曲线 图3 K1批次试验测温点温度

3 热误差模型建立与预测精度分析

以、轴方向热误差为例，利用多元线性回归模型，分别采用传统方法和模块化方法对该方向热误差进行建模和预测精度分析，验证模块化建模方法的稳健性。

预测残余标准差的大小用于表示拟合或预测精度，残余标准差越小，表明拟合或预测误差越小，精度越高。其计算公式为

(6)

3.1 传统热误差建模方法

将敏感点温度代入多元线性回归算法进行建模，结合2批次、方向上的数据建立模型1、1、2、2。

1：=7.23+5.87-0.4

2：=7.62+5.21+0.42

1：=-4.97-3.10+0.46

2：=-6.99-2.66+0.83

基于、和、代入多元线性回归算法建立的各批次模型，相互预测的残余标准差如表3所示，其中拟合看成模型对自身的预测。用多元线性回归模型对K1批次试验进行预测，结果如图4所示。

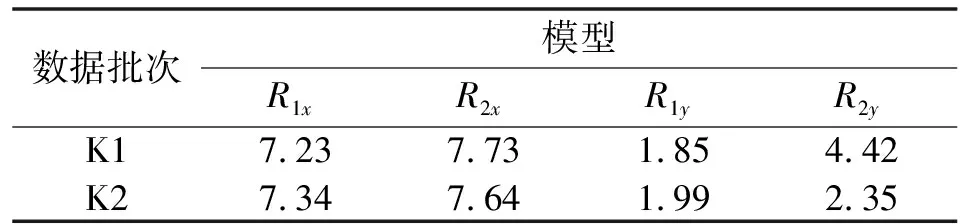
表3 传统建模方法的多元线性回归模型的预测残余标准差 单位:μm

图4 模型R1x在主轴x、y方向上的热误差预测值

3.2 模块化热误差建模方法

针对数控插齿机固有的结构引起的波动性的热变形，采用简单实用的平均法对图3所示的热误差曲线进行数据处理，对处理后的数据采用传统的建模方法。

计算公式为

(7)

式中：～为热误差测量值；()～()为数据处理之后的热误差值。

根据式(7)，得到各批次试验处理后的热误差数据如图5所示。

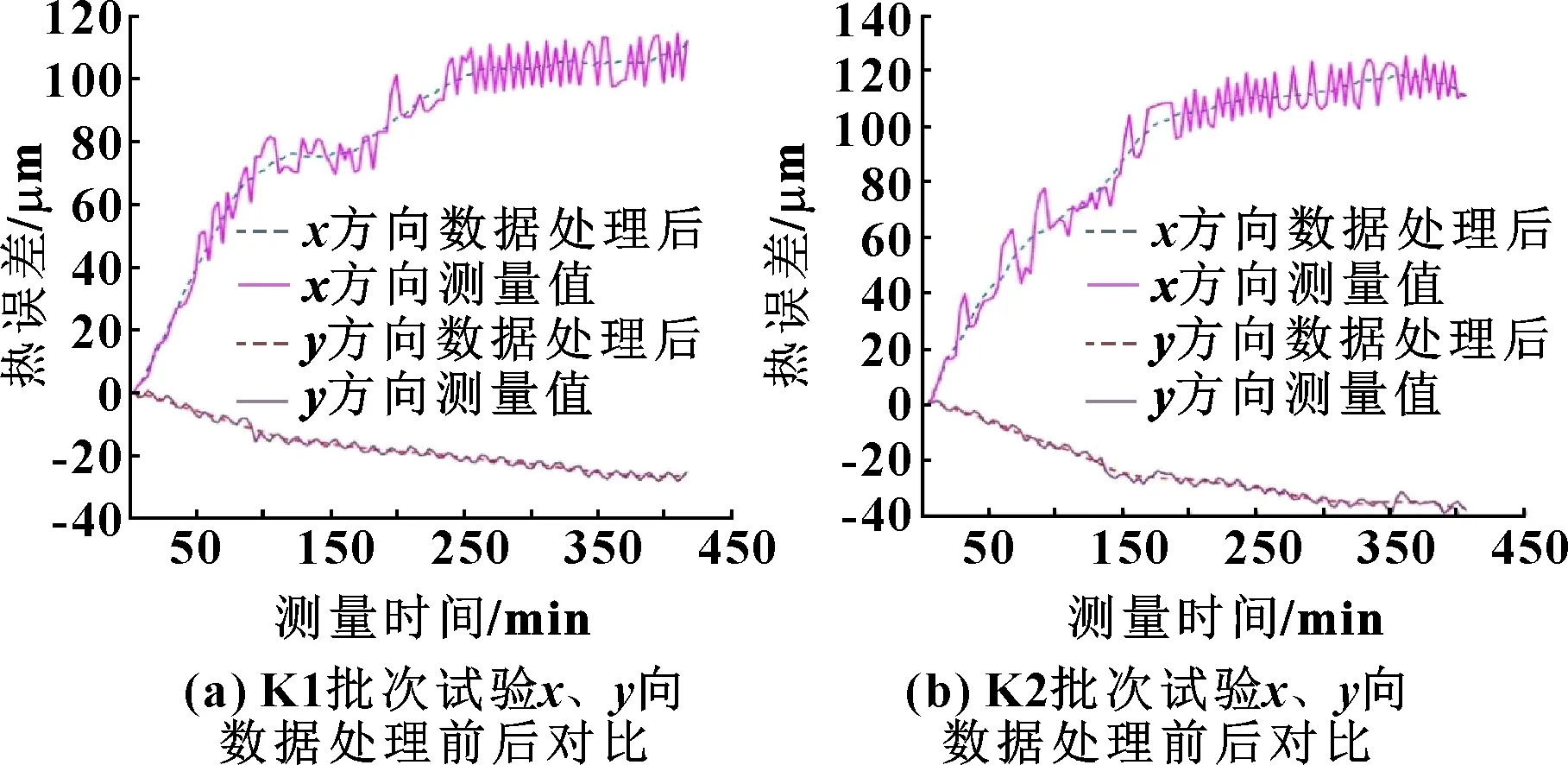
图5 各批次试验x、y向数据处理前后对比

将敏感点温度代入多元线性回归算法进行建模，结合2批次、方向上的数据建立模型′1、′1、′2、′2。

′1：=7.40+5.65-0.28

′2：=7.65+5.16+0.22

′1：=-4.96-3.09+0.43

′2：=-6.98-2.64+0.74

基于、和、代入多元线性回归算法建立的各批次模型，对K1、K2批次、方向处理前的数据进行预测，相互预测的残余标准差如表4所示，其中拟合看成模型对自身的预测。

表4 模块化建模方法的多元线性回归模型的预测残余标准差 单位:μm

从表3和表4可以得出以下结论:

(1)两种建模方法对主轴向的预测残余标准差都很稳定，相差不超过1 μm，说明模型1、2、′1、′2具有稳健性。

(2)对于主轴向来说，模型2、′2对K1批次的预测残余标准差(4.42、4.48 μm)比模型1、′1对K2批次的预测残余标准差(1.99、1.98 μm)约高3 μm。说明利用K1批次建立的模型对K2批次的稳健性比利用K2批次建立的模型对K1批次的稳健性较差。

(3)对于K1批次，模块化建模方法的模型′2的预测残余标准差(7.68 μm)低于传统建模方法模型2的预测残余标准差(7.73 μm)。

3.3 稳健性精度分析

根据K1、K2的温度数据,用上述模型对数控机床主轴在、方向热误差进行预测。

模型对主轴向的预测残余值的分布范围如表5所示。

表5 K1批次数据在主轴x方向的预测残余值分布范围

模型对主轴向的预测残余值的分布范围如表6所示。

表6 K1批次数据在主轴y方向的预测残余值分布范围

由表5、表6可知：

(1)传统建模方法在主轴向的预测残余值分布范围在0～12 μm 的概率(90%)大于模块化建模方法的概率(89%)，模块化预测残余值在不同范围的分布较均匀，说明模块化建模方法具有较高稳健性。

(2)传统建模方法在主轴向的预测残余值分布范围在0～8 μm 的概率(96%)大于模块化建模方法的概率(95%)，模块化预测残余值在不同范围的分布较均匀，说明模块化建模方法具有较高稳健性。

4 结论

(1)针对数控插齿机固有的主轴进给系统出现热误差波动性热变形，采用平均法处理数据，并提出模块化建模方法，以模糊聚类方法和多元线性回归建立了误差补偿模型。与传统建模方法相比较，模块化建模方法模型的稳健性得到了有效提升。

(2)模块化建模方法具有积极理论意义及较好前景，计划将此模块化补偿方法在五轴机床中进行应用和验证，同时针对不同型号机床的特殊性进行分析，将模块化处理方法推广应用。