基于粒子群算法的大口径高精度射电望远镜旋转编码器快速校准方法研究

侯晓拯，许 谦,2,3*，梁 娟,4，易乐天，薛 飞，王 惠

(1. 中国科学院新疆天文台，新疆 乌鲁木齐 830011；2. 中国科学院射电天文重点实验室，江苏 南京 210033；3. 新疆射电天体物理实验室，新疆 乌鲁木齐 830011；4. 中国科学院大学，北京 100049)

大口径射电望远镜在高频天文观测时，对天线盲指精度和跟踪精度要求极高, 一般而言，射电望远镜指向精度要求为最高观测频率半功率宽度(Half Power Beam Width, HPBW)的10%[1]。以美国国家射电天文台的绿岸射电望远镜(Green Bank Telescope, GBT)为例，指向精度最高可达3″，跟踪精度最高可达1.3″[2]。我国正在建设的新疆110 m口径全可动射电望远镜(QiTai Radio Telescope, QTT)[3]，最高观测频率为115 GHz，预期最高设计指向精度优于2.5″，跟踪精度优于1.5″。旋转编码器结构简单，精度高，体积小，重量轻，抗干扰能力强，常作为天线伺服控制系统的主要传感器，用于角位移的高精度测量[4-5]。然而在真实工况中，编码器在天线轴系中的最终使用精度，除了受到编码器自身光机电器件的影响，还受到天线传动轴在运行过程中磨损、天线结构受环境影响的自身变化、内外部扰动等影响，因此，为了保障天线编码器的读数为真实角度信息，较为理想的是定期对编码器及对应的轴系进行综合校准。在天文观测中，天线的观测误差使用基于标准源观测数据的整体校准[6]，以提高短期观测精度。而针对长期观测精度，则需要分析扰动与误差来源，从而进行校准与补偿。在大口径高精度射电望远镜天线实际使用过程中，编码器精度显著影响伺服控制系统的性能，进而影响天线的指向精度[3]。一般而言，影响编码器测量精度的主要误差来源有码盘误差、细分误差、偏心误差、安装倾斜误差等[7-8]。为了减小编码器在天线上的使用误差，对编码器的连接方式、安装工艺都有很高的要求[9-10]。而针对编码器误差的校准，较高精度的校准方法有示波器校准、多面棱体校准、多齿分度台校准、高精度转台校准、建模校准[11-12]、用更高精度的编码器校准等[13-14]。然而，对于高精度编码器的校准，大多需要额外配置校准设备。以大口径高精度射电望远镜为例，编码器安装主要在望远镜的装调阶段，需要复杂的工装以及校准设备，且在望远镜运行初期无法达到最优编码精度，需要在望远镜实际观测中进一步建立环境载荷对编码器影响模型并进行修正，从而最终实现编码器精度校准。装调工作复杂，易受环境影响，且需要一段时间的修正编码器才能达到最佳效果。在望远镜进入正式观测后除非编码器故障，否则不能随时获取编码器的综合使用精度，尤其在进行高频段观测时，编码器微小的精度损失将导致天线指向偏差。望远镜指向性能是一个综合参数，影响其变化的因素较多，很难短时间判断编码器的影响因素。另外在一些对编码器的周期性校准有高时效的场合[15-16]，受制于望远镜的停机时长、现场条件、校准条件、成本、部署时效等问题，无法实施高标准的安装工艺，传统高精度校准方法也受到限制。

针对以上问题，本文提出一种利用伺服电机定速旋转校准编码器安装误差的方法，无须额外配置校准设备即可获取编码器误差。该校准方法不是单纯针对编码器本身，而是结合编码器、天线轴系以及编码器的工作环境综合进行校准。本文使用粒子群算法，基于群体中个体之间的信息传递及信息共享快速寻找最优解[17]，快速拟合误差曲线进而修正编码器的安装误差。此方法可以在条件受限的情况下降低编码器安装精度要求，在天线的长期运行中定期获取编码器的精度情况，为提高天线指向精度以及编码器系统的定期维护提供一种简易可靠的方法。

1 校准方法

旋转编码器作为一种角位移传感器，在理想状态下，与负载轴刚性连接，同轴、正交、同步旋转。当负载轴匀速旋转时，理想编码器采样值的斜率应保持不变。实际使用中，由于安装误差或内外扰动等原因，理想状态无法实现。编码器的测量值围绕匀速旋转的负载真实角位移波动，根据这一原理可以校准编码器，消除安装误差。

当负载轴匀速旋转时，编码器持续采样，之后根据采样的首尾值做斜率固定的匀速旋转参考线。参考线与编码器采样值相减，可以获得重复出现的波动误差。受限于负载轴匀速旋转的稳定性，误差可能出现低频的慢变漂移，可以通过去趋势算法消除。最后，根据波动误差的周期性特点，选取多阶正弦函数拟合误差。

拟合函数的参数可以通过粒子群算法快速计算得出。该算法通过初始化一群随机粒子，迭代找到最优解。在每次迭代过程中，粒子通过跟踪两个极值更新，pbest为单个粒子本身找到的最优解，称为个体极值；gbest为整个种群找到的最优解，称为全局极值。粒子仅具有两个属性：速度和位置。每个粒子在搜索空间单独搜寻最优解，记为当前个体极值，并将个体极值与整个粒子群的其他粒子共享，找到最优个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。粒子群各粒子按

vi+1=vi+c1ε(pbest-xi)+vi+c2ε(gbest-xi) ，

(1)

xi+1=xi+vi

(2)

迭代，其中，ε为随机数；x和v代表粒子状态；c为迭代率；pbest为个体极值；gbest为全局极值。校准后的编码器将实际采样值作为输入，采样值与拟合函数逐点相减后的校准值作为输出，实现实时校准。

2 校准平台

编码器运行环境如图1。该平台模拟真实天线的俯仰轴系统，由旋转编码器、波纹管联轴器和负载轴组成。负载轴一端连接编码器，另一端连接伺服电机。编码器为绝对式编码器，量程0～360°，精度为16位。安装编码器时仅通过目测与手动对齐，具有较大的安装误差，同轴度与正交度较差。编码器通过柔性波纹管与负载轴连结，确保其与负载轴同步旋转。

图1 编码器运行环境

3 校准实验

为了验证校准方法的有效性，我们设计了校准实验。控制编码器校准平台中的伺服电机匀速转动并通过旋转编码器采样，根据采样值，设置斜率相同的匀速参考曲线，以5转每分钟的速度旋转8圈，获得的采样数据和参考曲线如图2。

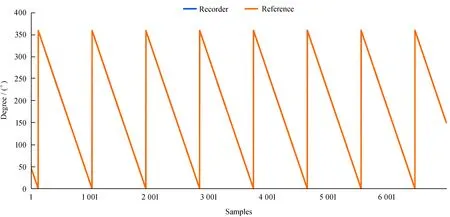
图2 采样数据和参考曲线

由于编码器与负载轴存在安装误差，采样必然出现周期性波动。将采样点与匀速参考点相减获得波动的编码器误差，并将其绘制在横轴为0～360°，纵轴为误差幅值的坐标系下，获得的编码器误差如图3。

最后，根据误差特点，选择正弦函数进行拟合。通过观察误差分布曲线，我们可以得出该误差分布与正弦曲线类似，故选取二阶正弦曲线，结合粒子群算法进行拟合，拟合公式为

y=a1sin(a2x+a3)+a4sin(a5x-a6)，

(3)

其中，a1～a6为待拟合的变量。将变量代入(1)式和(2)式，迭代求解拟合值y与实际传感器差值的最小值。当gbest迭代结果稳定后，拟合结果为

y=0.6sin(0.02x+0.24)

+0.12sin(0.036x-2.78) ，

(4)

其中，x为编码器读数；y为校准值。拟合后的编码器误差如图3中黑色曲线。

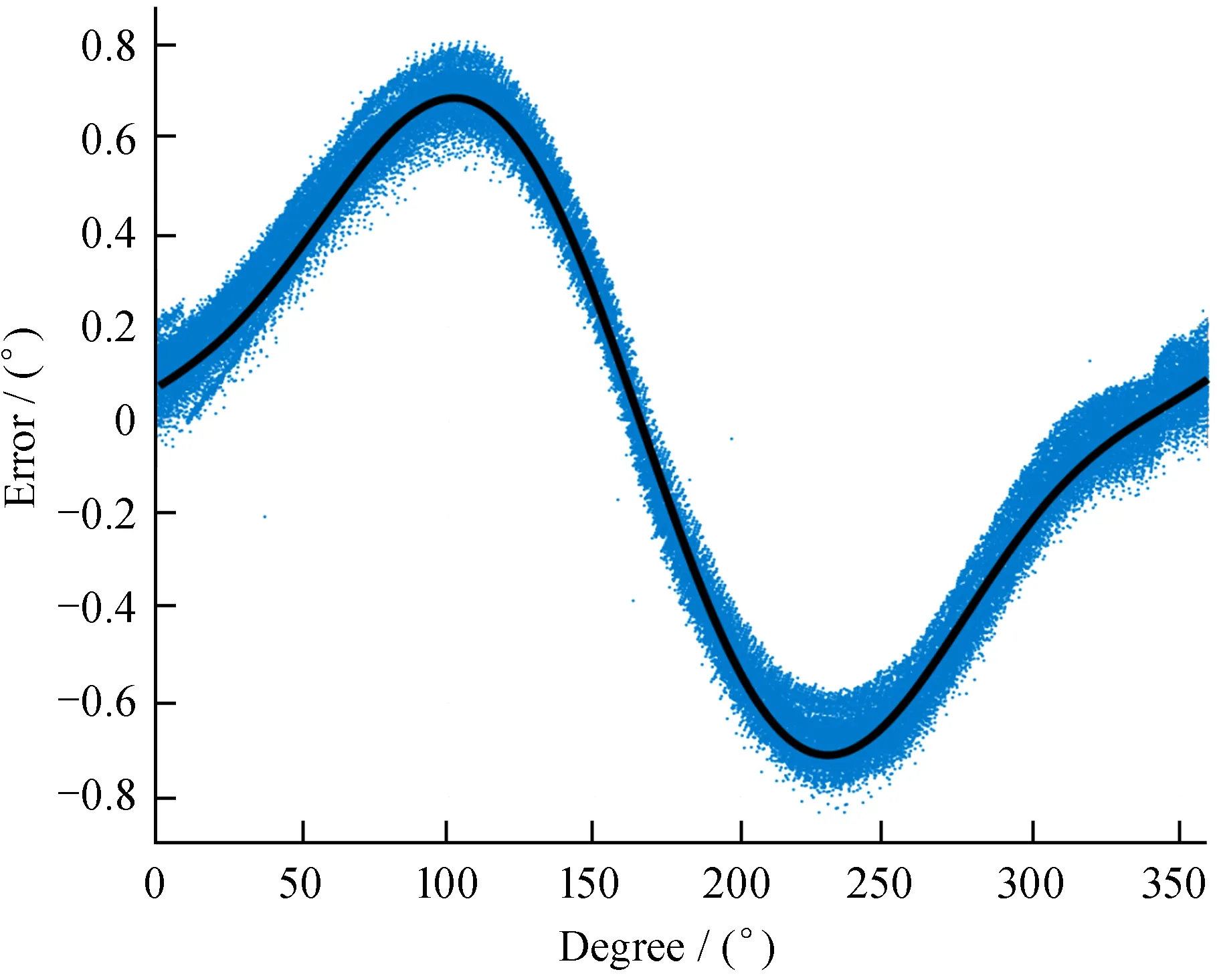
图3 编码器误差

利用(3)式作为校准函数，对编码器进行实时校准采样，获得校准后的残差如图4。图4中，蓝色曲线为编码器原始误差，红色曲线为校准后残差。对比可知，本工况中16位编码器的实际测量精度从初始状态的±0.85°，约7～8位，经过校准提高到±0.08°，约11～12位，精度提高超过10倍。与传统方法(如多面体棱台校准法，其典型校准精度约0.1″)相比，可以将低精度编码器的精度校准至设备固有精度极值。但传统方法在校准时，需要在待校准编码器或其传动轴上加装额外设备，且需要较长的校准时间，校准过程中不得有外部扰动。所以，传统的编码器校准方法虽然校准精度高，但用于大口径射电望远镜实际运行工况，面对风扰动、热形变、结构振动、天线结构的微小变化、测试设备安装环境、停机时长等问题，传统方法已经不是最优选择。

4 结 论

旋转编码器定速旋转的校准方法有效提高了编码器精度，校准过程仅需伺服电机带动编码器匀速旋转少量圈数，节省了校准时间。高分辨率旋转编码器在长时间的运行过程中，因振动、磨损等原因，测量状态 “精” 而不 “准”，且无法长时间停机维护，适合采用本方法，根据观测需求，灵活短时校准，从而快速提高望远镜的观测精度。