热流变复杂行为对沥青温度应力计算的影响

邱延峻，张 弘，谢清山，丁海波

(1. 西南交通大学 土木工程学院, 成都 610031；2.道路工程四川省重点实验室(西南交通大学)，成都 610031)

沥青的低温开裂是道路界普遍关心的问题，随着温度迅速下降，受限制的沥青面层会产生温度应力，当温度达到临界开裂温度Tcr时，路面就会产生开裂。这一现象严重影响路面的行驶舒适性，并可能严重损害沥青路面的耐久性。沥青胶结料是影响沥青路面开裂的重要因素，因此采用合适的方法确定沥青胶结料可适用的低温环境至关重要[1-2]。

很长一段时间以来，沥青都被视为热流变简单材料，满足时间温度叠加原理。但是研究者发现，当处于低温或者长时间加载时，沥青会出现热可逆老化现象，此时沥青的物理性能明显不符合热流变简单的特性[3-6]。热可逆老化是影响沥青低温性能评估的重要因素之一，研究表明，热可逆老化是一种随着恒温时间的延长，沥青材料会出现不断硬化的现象，这种老化与化学氧化老化不同，其可以通过加热而使沥青材料完全恢复到初始状态[7-12]。现有AASHTO沥青材料规范中有两种确定沥青低温等级的方法：一种是基于劲度(S)与蠕变速率(m)的经验性方法；另外一种就是通过理论计算温度应力，通过温度应力与断裂强度的比较确定低温等级[13]。与经验性的方法相比，温度应力计算的方法可以更好地反映沥青路面破坏的机理。因此，通过准确计算沥青胶结料的温度应力，能够有效地预测沥青路面地临界开裂温度，为评价寒冷地区的沥青道路开裂性能提供依据。

沥青的胶结料和混合料在温度应力计算原理上类似，只是在测试方法上存在不同。上世纪60年代研究者开发了几种沥青路面温度应力算法，并且一直沿用至今。第1种方法是由Hills和Brien(1966)[14]开发的简化的准弹性计算方法。在该方法中，假设路面为一无限长的受约束条带，采用准弹性梁的力学模型，使用弹性方程进行温度应力计算。第2种方法是由Muki、Humpreys和Martin等[15-16]开发以及后来被Monismith(1965)[17]采用的Hopkins & Hamming算法，此种方法按照严格的粘弹性理论，并使用了与温度相关的粘弹性材料参数，应力由Hopkins & Hamming[18]卷积积分进行求解。Hopkins & Hamming算法一直被许多研究人员使用到现在，并且在计算机应用开发之后变得非常流行。该方法被用于美国路面结构设计的两本规范AASHTO R-49-09(2013)和ASTM D6816-11(2011)。此外，还有相关文献中提到的一种“拉普拉斯变换法”[19]，此种方法原理与Hopkins & Hamming算法相似，遵循沥青材料的粘弹性特性，但却是通过蠕变柔量一步计算得到温度应力。

Hopkins & Hamming算法和“拉普拉斯变换法”仅适用于完全符合时间温度叠加原理的线性粘弹性和热流变简单材料。如果材料性质偏离了热流变简单特性，上述方法则不再适用。Jozef Judycki发现了一种考虑沥青混合料热可逆老化的温度计算方法，该方法从Burgers粘弹性模型出发，通过试验得到不同温度下材料的流变参数来计算温度应力，该方法被其称为“增量法”[20-21]，该方法对热流变复杂的材料也同样适用。但是，Jozef Judycki只是将这种计算方法应用到了沥青混合料中，为了验证“增量法”在沥青胶结料中是否同样适用，并且探讨热流变复杂行为对沥青结合料热应力计算的影响，本文进行了以下研究。

1 试验与材料

试验在弯曲梁流变仪(BBR)上进行，本文为两种算法都设置了0、-3、-6 ℃到-30 ℃共11个温度测试点，并且都在-18 ℃的恒温水浴箱中养护1 h和72 h后进行测试。两种算法在加载模式的设计有所不同，Hopkins & Hamming算法采用的是标准的BBR加载240 s、卸载10 s短期加载模式，而增量法采用的则是加载9 000 s，卸载1 800 s共3 h的长期加载，短期加载下得到的是60 s对应的刚度模量S和刚度模量变化率m，长期加载则是得到整个加载时间下的蠕变数据。

试验采用的是美国SHRP的未改性的3种基质沥青，分别是沥青试样A，试样B，试样C，3种沥青的流变性质和对温度的敏感性差别较大[22]，这也正是选择这3种沥青的原因。沥青的具体信息见表1。

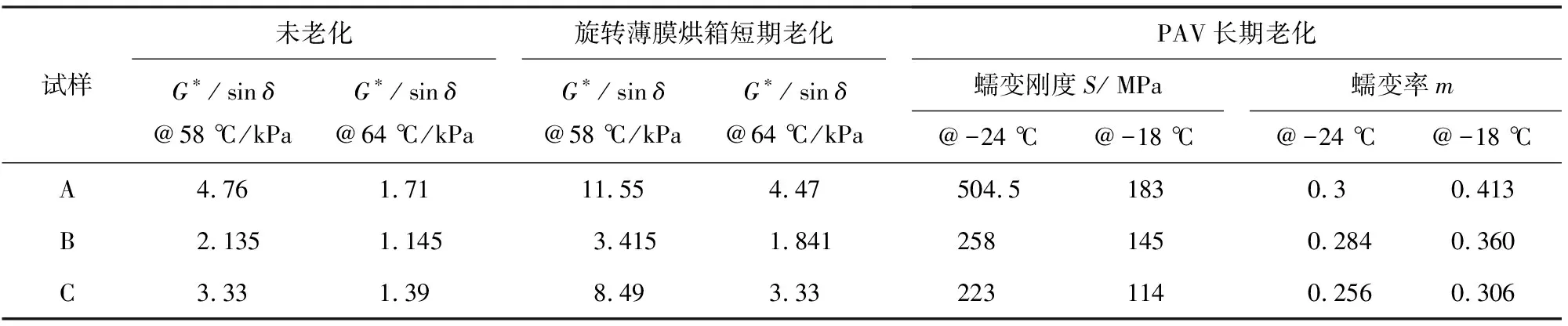
表1 试验采取的沥青结合料的相关信息

2 计算方法

2.1 Hopkins & Hamming算法

Hopkins & Hamming算法是通过BBR试验获得沥青的劲度模量，通过系列转换得到蠕变柔量和松弛模量，最终的温度应力计算公式为

(1)

其中：σ(t)为温度应力随时间的变化，E(t)为松弛模量随时间的变化，ξ为转化时间，为温度应变[23]。

2.2 增量法

该方法以粘弹性体的Burgers元件为理论基础模型，该模型的结构元件如图1所示。Burgers模型的本构方程[24]为

(2)

其中：P1=η1/E1+(η1+η2)/E2，P2=η1η2/(E1E2)，q1=η1，q2=η1η2/E2，E1为瞬时弹性模量，E2为延时弹性模量，η1为稳定流动黏度系数，η2为延迟流动黏度系数。

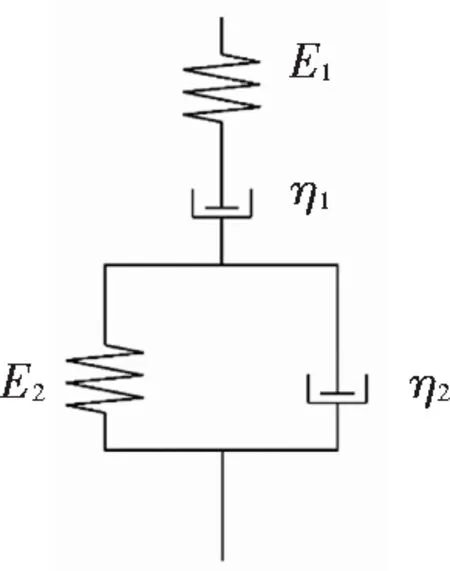
图1 Burgers模型

现作出如下假设：路面层具有恒定的流变参数，并且沥青层的温度随时间以恒定速率VT变化，在给定的时刻，在层(x，y，z)的每个点所处温度是相同的。图2展示了沥青层的结构特点，沥青层恒定厚度中的平面(x，y)具有无限的尺寸，而该层在z方向上可以自由地改变尺寸，所以当温度变化时，在平面(x，y)中的层中产生的温度应力σx=σy≠0，在z方向(沥青层的深度)产生的温度应力σz=0[21]。

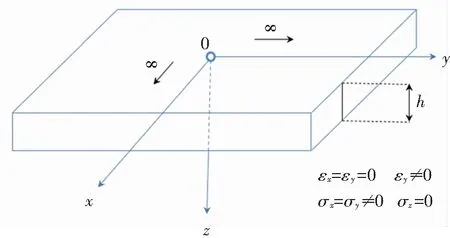
图2 沥青层图示

温度在假想自由层中以恒定速率VT随时间变化为ΔT，则发生电位应变ε(t)为

(3)

其中：αT为热膨胀系数，ν为泊松比。

将ΔT(t)用VT·t代替，并在等式两边分别对时间求一次、两次导得到应变ε(t)与时间的导数关系为：dε/dt=αT·VT·1/(1-ν)；d2ε/dt2=0。将其代入Burgers本构方程得

(4)

其中Vε=αT·VT·1/(1-ν)表示自由沥青层中假设的温度应变率。

上述等式是关于应力σ与时间t的二阶线性非齐次微分方程，按照以下初始条件进行求解：在t=0时，ε=0，σ=0，dσ/dt=E1·Vε。得到该方程的解为

(5)

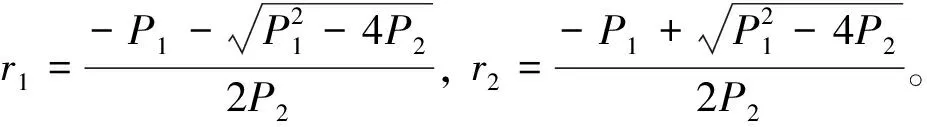
图3展示了各种热力学参数随时间t和温度T的变化。本方法中温度按恒定速率变化，假定在一小段温度变化ΔT内，沥青层的参数是恒定的，按照一个ΔT为一个小步骤，将整个温度变化过程划分成这样n个步骤，每个步骤中i(i=0,1,…,n)的流变参数是恒定的，且可能会在下一步i+1中发生变化。当温度从T0变化到Tn时，对应的t0=0变化到tn=(Tn-T0)/VT，用Δti=ti+1-ti表示第i步的时间区间，ΔTi=Ti+1-Ti表示第i步的温度区间，Si表示第i步流变参数的集合{E1,i，E2,i，η1,i，η2,i，νi，αTi}。

(a) 弹性模量E1随时间t和温度T的变化

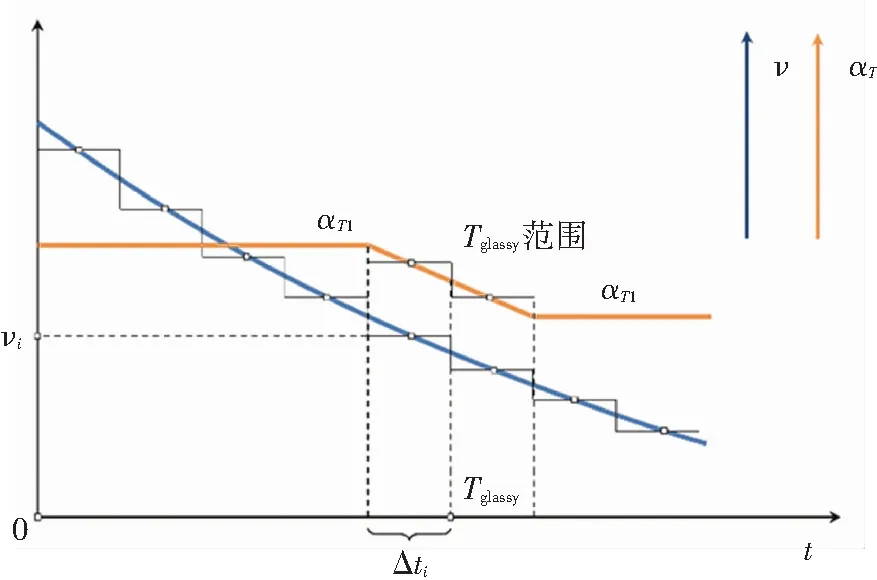
(b) 泊松比ν和热膨胀系数αT随时间t和温度T的变化

计算第i步(i=0,1, …,n)的温度应力σ(Si,t)由式(5)进行求解，然后，当温度从Ti-1变化至Ti时，流变参数的改变会引起温度应力的增加(或减少)，用Δσi(τ)表示第i步由于流变参数变化引起的应力变化值，其中τ表示流变参数由i-1状态转化至i状态下的转化时间，本方法的图解说明如图4所示，Δσi(τ)的计算公式为

Δσi(τ)=σ(Si,τ)-σ(Si-1,τ)

(6)

其中σ(Si,τ)，σ(Si-1,τ)都由式(5)进行求解。

时间t的温度应力最终的计算公式为

σi(t)=σi-1(t)+Δσi(τ)

(7)

其中：σi(t)表示第i步的实际应力，σi-1(t)表示上一步i-1的实际应力，Δσi(τ)表示从i-1到i的应力增量。

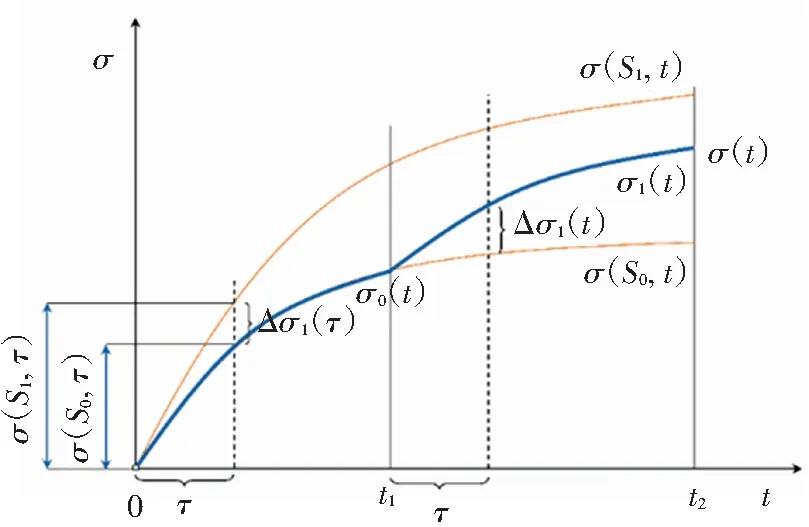
(a) 有两个步骤(i=0,1)

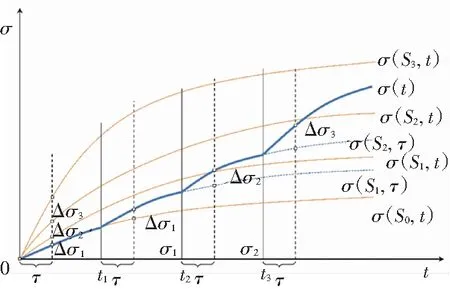
(b) 有4个步骤(i=0,1,2,3)

式(5)所需的各个温度下的流变参数，是通过BBR试验得到的蠕变数据，结合Burgers流变模型的应变-应力关系式：

(8)

将得到的数据代入该方程，拟合得到该测试温度下的流变参数E1，E2，η1，η2[25]。

3 结果与分析

3.1 两种方法结果对比

在短期加载模式下得到的60 s下的劲度模量S和劲度模量的变化率m，在长期加载模式下得到的蠕变数据，降温速率取3 ℃/h，泊松比和热膨胀系数取常量分别为0.25和1.71×10-4，通过上述计算方法即可得到两种方法计算出的温度应力，选取养护时间为1 h的结果如图5所示，通过图5可以看出，整体来看，两种方法大致吻合，但是在较低的温度下，增量法普遍比Hopkins & Hamming算法算出的结果大一些，这是因为增量法采用长期加载的模式，更加符合真实的情况，这种方法考虑到了材料偏离时间温度叠加原理时，材料由于热可逆老化引起的温度应力的增加，而传统的温度应力计算由于没有考虑这一部分硬化的影响，在较低温度下则会低估温度应力。具体来看，在-30 ℃时，3种材料在两种计算结果下的差值分别为0.041 MPa(试样A)、0.139 MPa(试样B)和0.068(试样C)，这说明试样A的流变性能最简单，试样C其次，试样B最复杂，这与已知的材料流变性能是相符合的。

(a)试样A

(b)试样B

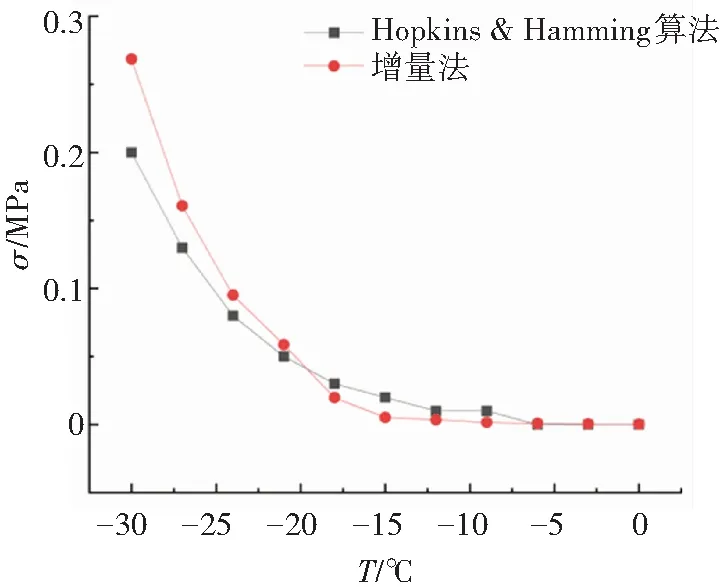
(c)试样C

本文还考虑了不同的降温速率对对比结果的影响，图6是用增量法计算的试样B在不同降温速率下的结果，可以看出各个降温速率下的应力随温度变化的趋势相同，在-15 ℃之前随温度降低应力变化很小，低于-15 ℃之后随温度变化显著。这种趋势在两种计算方法中是一致的，并且，不同降温速率下两种方法的对比结果也是相同的，因此在对比两种方法的时候并不需要讨论降温速率的影响。

图6 试样B不同降温速率计算结果

3.2 不同养护时间结果对比

图7展示了3种沥青结合料养护1 h和养护72 h后的增量法计算对比结果，可以发现，3种材料在养护72 h的情况下普遍比养护1 h的结果要大，这是符合常理的，长时间的低温养护使材料发生明显的硬化现象。但是各个材料在不同养护时间下的变化趋势则不同，试样B这种沥青在两种养护条件的差值最大为1.025 MPa，而试样A和C的差值则较小，分别为0.097 MPa和0.217 MPa，这说明低温养护处理对材料的硬化效果与材料的流变特性相关，热流变简单的材料受低温硬化效果较小，热流变复杂的材料则在低温养护下的硬化效果十分明显，原因是热可逆老化在其中起到了很大的作用，一些研究者将沥青中的蜡含量与热可逆老化联系起来，认为蜡的结晶析出是材料发生热可逆老化的一种解释，所以推测这种硬化效果很可能与蜡的低温结晶有关。

(a)试样A

(b)试样B

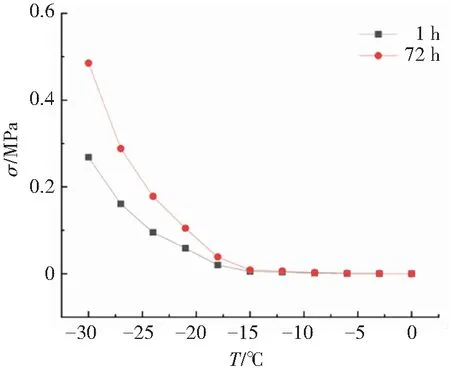
(c)试样C

3.3 主曲线验证时间温度叠加原理

将参考温度设置为-18 ℃，其他温度下的刚度数据按照位移因子进行平移得到刚度主曲线，图8展示了3种沥青结合料养护1 h后的主曲线。如果材料完全符合时间温度叠加原理，得到的主曲线将会是完全重合的一条线，这条线描述了材料在整个温度和加载时间范围内的力学性质。从养护1 h后3种材料的刚度主曲线来看，只有试样A这种沥青的主曲线比较好地重合，其余两种则是出现了不同程度的偏离，这很好地对应了3种沥青的流变性质。试样B主曲线100 s左右之后出现了明显地偏离，-21 ℃下的曲线偏势更大，试样C的偏离则出现在-30 ℃的曲线上，这证实热流变复杂的材料偏离时间温度叠加原理一般是在长期加载和温度较低的条件产生的。出现的偏差与加载时间密切相关，这正是本文采取长期加载模式的意义，很多热流变复杂的沥青在短期加载下同样很好地满足时间温度叠加原理，显示出热流变简单的特性，这也是传统计算方法的弊病，这种判断上的错误会导致人们忽略实际情况下热可逆老化带来的影响，很多道路的低温开裂便由此而来。不同沥青出现偏差的最高温度值也有显著差异，在此推测该值的大小可能与沥青本身的粘弹性特性有关。

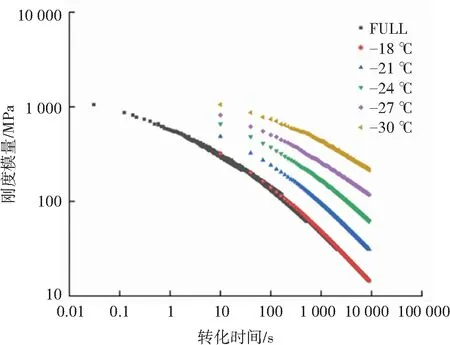
(a)试样A

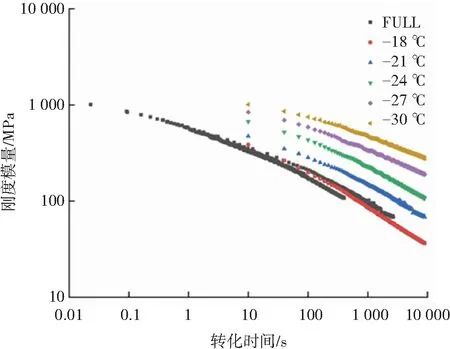
(b)试样B

(c)试样C

4 结论与展望

1) Hopkins & Hamming算法与增量法的温度应力计算结果基本吻合，但在较低的温度下，Hopkins & Hamming算法未考虑热可逆老化带来的影响，其结果与增量法相比偏小。增量法采用长期加载的模式，更加符合真实情况，无论是热流变简单材料还是热流变复杂材料，这种方法都是适用的。

2) 不同降温速率下，温度应力值的大小不同，但是随温度的变化趋势都是一致的，在-15 ℃之前温度应力变化缓慢，-15 ℃之后快速增加，两种计算方法的对比中不需要讨论降温速率的影响。

3) 低温养护对沥青的硬化作用与沥青的流变性能相关，热流变性能越复杂的沥青，低温硬化的效果越明显，反之硬化效果则不那么显著。

4) 通过主曲线验证时间温度叠加原理发现，当沥青处于长期加载时，只有热流变简单的沥青是完全符合时间温度叠加原理的，现有的计算方法和规范一般采用240 s的短期加载模式，在预防低温开裂和评估沥青流变性质等方面存在一定的局限性。

5) 增量法的适用性需要更多的试验进行验证，未来会对不同蜡含量、组分的沥青以及沥青混合料进行验证试验。