浅埋隧道顶管掘削施工的地层扰动安全风险控制研究＊

徐 浩，张毅峰，郭爱国

（1.中铁高新工业股份有限公司，北京 100070；2.西南交通大学交通隧道工程教育部重点实验室，四川 成都 610031；3.长沙中大建设监理有限公司，湖南 长沙 410000）

随着城镇化的建设发展，城市建设者们纷纷将目光投向广阔的地下空间，众多的给排水管道、过街通道、综合管廊、地铁出入口通道、地铁联络通道市政项目纷纷采用顶管技术。

目前，众多学者针对顶管施工进行了研究，研究方法大多集中在数值模拟、现场监测以及相似实验等方面。

在数值模拟上，学者对顶管隧道的开挖建立数值模型分析，分析总结开挖扰动对周围围岩的影响以及拱顶沉降变化规律[1-3]。如SENDA 等[4]、HAN 等[5]分别采用数值模拟研究了不同围岩参数下顶管隧道开挖对周围地层的扰动以及隧道拱顶的位移变化规律。许有俊等[6]依托内蒙古某地下通道顶管工程，研究了不同支护应力比时砂砾石地层中矩形顶管掌子面主动破坏与被动破坏规律。随着数值计算的深入，逐渐有学者就盾构刀盘与土体的相互作用进行研究，刀盘转动前进过程中与土体接触关系十分复杂，目前尚无被广泛接受的理论解析。汤华等[7]和韩美东等[8]学者考虑土体材料非线性，引入单元失效准则实现土体脱落与删除，针对掌子面切削土体全过程仅仅数值模拟，分析在掘进过程中土体损失变化规律。蔡宝等[9]建立了3 种地层中不同切刀重叠量和切刀内偏角及刀具布置方式的刀盘开挖数值模型，得到了岩土质量随掘进时间减少的规律，并通过刀盘受力分析了不同地层的刀盘适应性。严战友等[10]建立三维离散元地层模型，用初始地层应力等效考虑隧道埋深影响，研究了隧道埋深、刀盘振动对刀盘推力、扭矩及不同阶段开挖区域土体颗粒位移的影响。

现场监测是科学研究一大方面，邓长茂等[11]对上海软土地层三个大断面顶管工程进行分析，总结出最大地表沉降均靠近始发井，顶管机通过25 m 后地面沉降基本稳定。李刚[12]根据顶管施工现场地面位移监测值，研究了单个顶管掘进和平行顶管先后施工的地层扰动规律。YOU[13]将拱北隧道曲线管幕顶管引起地表变形的有限元模拟结果和现场监测数据进行对比，验证了三维有限元模型的可靠性，并提出泥浆套连续性、掌子面压力是地表变形的主要影响因素。

同时也有学者通过建立实验总结开挖中的变化规律，如江英超[14]针对砂卵石地层盾构隧道开挖进行室内试验和离散元模拟，从土体位移和地层应力角度研究了盾构掘进对砂卵石地层的扰动特性。

上述研究工作集中于盾构刀盘这一部分，忽视了后续管节与管周土体间的相对滑移摩擦影响，对顶管真实扰动模拟情况的借鉴价值有限。本文针对浅埋圆形顶管工程，建立了包含刀盘、管节的数值模型，考虑刀盘的转动切削和管土相互作用效应，分析了在开挖过程中地表位移变化规律、地中位移变化规律以及掌子面的切削过程，可为顶管真实扰动模拟提供借鉴参考。

1 土体剪切失效破坏

利用有限元在模拟隧道开挖时常采用刚度迁移法，其不考虑单元体是否达到屈服状态，直接将人为定义区域单元的刚度乘上一个极小的减缩系数，以实现单元的钝化功能，但刚度矩阵保持不变。刚度迁移法模拟过程简单，但并未将刀盘与围岩间的相互作用考虑进去，不适用于顶管刀盘连续转动、掌子面土体逐渐破坏的施工过程模拟。鉴于此，引入单元损伤失效准则，通过对土体单元材料定义剪切失效判断标准，由软件自行计算损伤变量，对单元状态变量STATUS赋值确定单元是否完全失效，若达到失效标准，则将单元从模型中删除，不再参与计算。

2 有限元数值模型建立

顶管埋深4.0 m，管节外径3.0 m，总长7.5 m，幅宽1.5 m，厚度0.15 m，不单独考虑顶管机钢壳；管节采用各向同性均质弹性材料，忽略管节接头效应。刀盘类型为面板式，开口率67%，仅考虑中心刀和切刀。由于实际工程中刀盘开挖断面、顶管机壳体和管节轮廓有一定差异，将刀盘外径设置为3.02 m。刀盘刚度一般远超过土体和管节，其变形可忽略，在模型中设置为刚体。

2.1 地层参数

简化模型地层为单一均质地层，地层土体物理力学性质参数如表1所示。

表1 地层土体物理力学参数

2.2 边界条件

地层和结构完整有限元模型网格如图1—图3所示，全部模型网格共包含23.5 万个单元。综合考虑顶管施工扰动范围与计算成本，地层模型横向宽度、竖向高度、纵向长度分别为16 m、16 m、10 m（X、Y、Z），对底面和4个侧面施加法向位移约束。对于裸露在土体外部的顶管管节，约束其底部部分节点竖向位移；对于约束刀盘横向、纵向位移，仅允许其纵向推进和面内转动。

图1 有限元模型网格

图3 刀盘放大模型

2.3 顶管施工过程模拟

按照实际施工情况，在刀盘中心参考点施加转动角速度和纵向顶推速度，在管节尾部施加纵向顶推速度。参考贯入度取为30 mm/r。为节约计算时间，同时对刀盘转速和掘进速度适当放大，最终刀盘转速为0.63 rad/s，合6 r/min；结构掘进速度为0.003 m/s，合18 cm/min。

在开挖临空面上施加均布的径向注浆压力，注浆压力取值为0.08 MPa。

刀盘与土体、管节与土体之间均设置面面接触，切向仍采用罚函数法设置摩擦系数，刀盘表面与土体间摩擦系数为0.1，管节表面与土体间摩擦系数为0.25。

图2 刀盘-顶管结构模型

3 结果分析

3.1 地表位移

图4 给出了考虑刀盘掘削土体效应的顶管施工地表位移，可见地表横向与竖向位移整体上具有对称性，但由于刀盘的转动，轴线两侧纵向位移分布有一定差异。顶管两侧地表横向位移最大，超过3 mm；地表竖向位移均为沉降，在顶进范围内沉降最为明显，最大沉降为18.1 mm；顶进范围内地表土体向始发端移动趋势明显，掌子面上方土体纵向“回移量”达到3.4 mm，且更靠近掌子面右侧，这是由于沿顶进方向刀盘顺时针转动，在右侧带动土体向下移动，掌子面前方土体更容易涌入洞内，带动上方土体回移。

图4 刀盘掘削顶管模拟地表位移结果

总结Z=1.2 m 横断面在地表不同顶进阶段的位移变化，绘制曲线得到图5。由图5（a）可知对于Z=1.2 m横断面，横断面地表始终呈沉降状态，且随着掌子面的接近沉降值逐渐增大，边界处地表沉降也较大是由于模型尺寸过小。在掌子面到达监测横断面时轴线上方地表沉降达到14.0 mm，随后缓慢增大，到掌子面通过监测横断面1.2 m 后，地表沉降趋于稳定，约为16.8 mm。

图5（b）中靠近边界处位移存在不规则波动，这是地层模型尺寸过小引起的，因此，仅分析中央靠近顶管区域地表纵向位移发展趋势。中央地表纵向位移方向始终与顶进方向相反即发生“回移”，当顶管尚未到达监测横断面且掌子面与监测横断面纵向距离超过0.6 m 时，回移量随着顶管的靠近而逐渐增大；监测横断面位于掌子面前方0.3 m 处时，中央地表回移量减少，但随后又有所增加；掌子面通过后，中央区域地表纵向位移基本稳定。

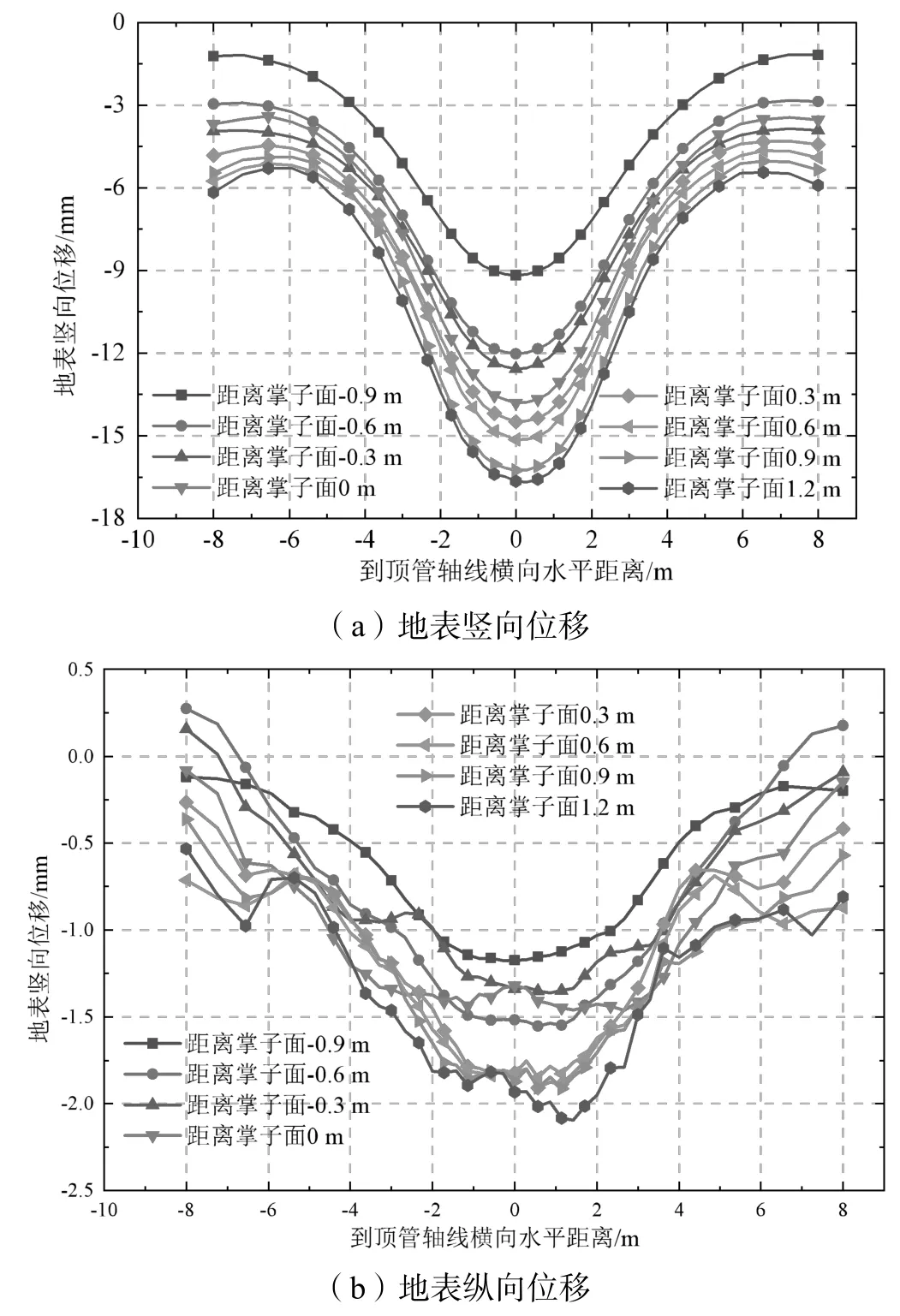
图5 不同顶进阶段地表位移横向分布（Z=1.2 m 横断面）

顶管轴线上方地表竖向位移纵向分布变化如图6所示。由图6 可知，掌子面前方地表土体竖向位移均为沉降。随着顶进距离的增加，轴线上方地表沉降增加，但在顶进0.9～1.8 m 阶段，到始发端纵向水平距离5.5～7.5 m 范围内轴线地表沉降基本不变，远离始发端模型边界处地表竖向沉降曲线下降，原因包括掌子面前方深层土体向洞内移动和边界纵向位移约束。由于分析顶进长度较小，地表沉降发展规律并不清晰。

图6 顶管轴线上方地表竖向位移纵向分布变化

对轴线上方地表纵向位移发展进行分析，如图7所示。掌子面前方一定范围内土体纵向位移方向与顶进方向相反，轴线地表纵向位移值整体上随着顶进长度的增大而增大，但有部分时刻地表纵向位移较前一阶段有所减小，原因是刀盘转动掘削时，掌子面土体轮流与面板、开口接触，土体受到的支护作用持续变化，引起了轴线地表土体纵向位移的不规则变化。

图7 顶管轴线上方地表纵向位移纵向分布变化

3.2 地中位移

提取Z=0.6 m、Z=1.5 m 横断面上到顶管轴线横向水平距离等于﹣6 m、﹣3 m、0 m、3 m、6 m 处土体纵向位移沿深度分布曲线，如图8所示。可见，轴线两侧对称位置处深层土体纵向位移基本相同，并不受刀盘单向转动切削的影响；顶管深度范围内土体纵向位移与顶进方向相同，且明显大于其他深度区域土体，随着与顶管轴线横向水平距离的增大，土体纵向位移逐渐减小；掌子面后方0.9 m 处，拱顶中央土体纵向位移最大，约12 mm，仰拱中央土体纵向位移约5 mm；掌子面上拱顶与仰拱中央土体纵向位移较为接近，分别为25 mm、24 mm。

图8 顶进1.5 m 时土体纵向位移沿深度分布

比较2个监测横断面纵向位移结果，可知：掌子面中央深层土体纵向位移约为掌子面后方0.9 m 横断面上相同位置处土体纵向位移的2 倍，说明刀盘掘削时对掌子面前方土体具有显著支承作用，对深层土体纵向位移影响较大，此外，掌子面中央区域内土体纵向位移明显小于刀盘边缘处土体，反映了掌子面中央区域内土体向洞内涌入的趋势。

3.3 掌子面变形

对掌子面土体变形进行分析，图9 为刀盘从开始转动到在土体中完整旋转一周过程中不同时刻掌子面形态，根据刀盘与土体初始距离及刀盘顶进速度计算相应时刻的刀盘顶进距离，可知：1.0 s 时刀盘中心刀贯入土体0.001 m，切刀尚未接触到土体，此时拱顶土体有沿顶进方向的较小位移，掌子面下方土体纵向位移方向相反，量值较小，中心刀接触区域纵向位移大于周围土体；8.0 s 时中心刀贯入土体0.015 m，切刀即将接触掌子面土体，此时中心刀切削土体引起掌子面中心区域显著纵向位移；10.0 s 时中心刀贯入土体0.019 m，切刀贯入土体0.004 m，且在土体中旋转72°，此时掌子面出现切刀旋转引起的沟槽，到11.0 s 时从切刀接触土体开始刀盘转动108°，切刀转动沟槽进一步发展；18.0 s 时，切刀在土体中已转动一周，掌子面土体全部被刀具切削轨迹覆盖。

图9 不同时刻掌子面土体形态

进一步探究特定掘进段中刀盘表面接触的土体形态，如图10所示，在对应掘进段前进47.0 s 为比较基准，此时刀盘下半区域已有少部分土体被削除，出现空洞区；前进57.0 s 时，刀盘转动一周，刀盘下半区域土体大致削除完成，仅在中心刀和边缘区域有部分残余土体，上半部分土体空洞区亦开始发展；再旋转一周后（67.0 s），刀盘正面土体已基本掘净，极少量土体附着；最终，结构前进77.0 s 时，原先与刀盘表面接触的正面土体全部删除，仅在边缘处存在少量因断面差异而未被掘削的土体单元。

图10 与刀盘表面接触的土体形态

4 结论

以浅埋圆形顶管工程为例，建立了包含刀盘、管节的数值模型，考虑刀盘的转动切削和管土相互作用效应，分析对地层扰动安全风险控制措施，得出如下结论。

地表横向与竖向位移具有对称性，但由于刀盘的转动，轴线两侧纵向位移分布有一定的差异；顶进范围内地表土体纵向“回移”趋势明显，且沿着顶进方向刀盘顺时针转动导致右侧上覆土体向下移动，进而引起掌子面土体进入洞内。

在靠近顶管的深层土体中，掌子面左右两侧的监测点各向位移总体上保持一致，位移主要发生在横向上；掌子面中央深层土体纵向位移约为掌子面后方0.9 m横断面上相同位置处土体纵向位移的2 倍，掌子面中央区域内土体纵向位移明显小于刀盘边缘处土体。

掌子面在被刀盘掘削过程中，8.0 s 时中心刀贯入土体0.015 m；10.0 s 时中心刀贯入土体0.019 m，切刀贯入土体0.004 m，且在土体中旋转72°；11.0 s 时从切刀接触土体开始刀盘转动108°；18.0 s 时，切刀在土体中已转动一周，掌子面土体全部被刀具切削轨迹覆盖；最终第77.0 s 时，原先与刀盘表面接触的正面土体全部删除，仅在边缘处存在少量因断面差异而未被掘削的土体单元。