类比思想在高中数学课堂教学中的应用研究
2022-09-17朱国防
◎朱国防
(山东省单县第五中学,山东 单县 274300)
高中数学知识本身具有较强的抽象性、综合性,很多学生在学习过程中会由于不理解其内容而出现挫败感同时,高中数学教师在教学过程中如果沿用传统的灌输式教学手段,也会引起学生的厌烦感,不利于学生数学核心素养的提升对此,在教学实践中,高中数学教师可以采用类比思想,让学生在类比过程中充分掌握新、旧知识,促进学习效果的提升
1 类比思想在高中数学教学中的重要性
1.1 激发学生主动学习的热情
类比思想本身具有很强的创造性,其可以引导学生将不同事物放在一起进行比较、归纳,使其更具想象力在高中数学教学中,教师采用类比方法能给予学生更加广阔的联想空间,使学生在学习中能够进行从一般到一般、从一般到特殊、从特殊到特殊、从特殊到一般的类比推理,既加深对知识的理解,又建立正确的解题思维,对其数学探究欲望的提升有很大帮助
1.2 强化学生的数学类比思维
在高中数学教学中,教师培养学生的类比思维可以指引学生学会用熟悉、已知的知识类比未知的内容,这样他们就会在寻找知识与知识的关联中提高自身的思维能力在近几年的高考中,类比是一个比较热点的话题,其既考查了学生本身的研究能力、知识掌握能力,又考查了学生的推理能力故教学中类比思想的引入可以让学生更加熟练地解决一些复杂的数学问题,强化数学学习效果
2 类比思想在高中数学理论教学中的应用
2.1 应用类比思想进行教学的策略
高中数学教师在开展课堂教学活动时应该充分发挥自身的引导作用,指引学生在类比中掌握知识具体来说,在数学课堂上,教师可以按照以下几个环节渗透类比思想
(1)引导式提问教师针对目标问题设置一个学生比较熟悉的问题,让其通过对两者进行类比、思考,加深对知识的理解
(2)联想与辨别类比主要是通过推理的方式找出两个或多个对象在某方面的共同属性,然后进行联想、辨别在高中数学教学中,教师在引入类比思想时需要指导学生大胆假设,通过发散思维对问题进行分析、观察,在此过程中理解、掌握相关知识如学习圆锥、圆柱相关知识,学生可以通过辨别意识到圆锥是圆柱的一种特殊存在,并且在辨别过程中快速掌握圆柱、圆锥的特征在教学过程中,教师需要注意对学生进行有意识的点拨,借助类比思维让学生牢固掌握圆柱、圆锥知识,提升学习效果
2.2 案例分析
为了更好地研究在高中数学教学中应用类比思想的策略,下面结合“直线的斜率”这一知识点进行分析在课堂教学中,教师可以为学生创设爬山坡的情境,引导学生类比坡度与直线斜率,从而得到思维拓展,提升学习效果
进入课堂,教师应先与学生进行简单的对话交流,让学生思考“过几个点可以作一条直线”,学生很轻松地回答“2个点”接着,教师让学生思考“过一个点能作多少条直线”,学生回答“过一个点能作无数条直线”教师又让学生说出“这些直线都有什么不同点”,学生回答“这些直线的方向不同”教师根据学生的回答对学生进行引导——方向不同体现了直线的倾斜程度不同,同时让学生思考如何量化表示直线的倾斜程度教师为学生展示两个坡度不同的山,并让学生思考自己会爬哪一座山有的学生表示会选择爬坡度比较平缓的山,也有的学生表示会选择比较陡的山,这样更具有挑战性这时教师让学生思考可用什么样的方式描述山坡的平缓与陡峭在学生思考的过程中,教师启发学生联想坡度,随后让学生思考该如何计算坡度学生经过思考可以提出用高度除以宽度得出坡度接着,教师让学生思考坡度是指山的什么,然后利用多媒体给出相应的图片,启发学生意识到坡度是指山坡的倾斜程度随后,教师指引学生将坡面抽象成一条直线,放在直角坐标系中,山脚对应点,山顶对应点,如图1所示,该如何表示这一“山坡”的倾斜程度呢?
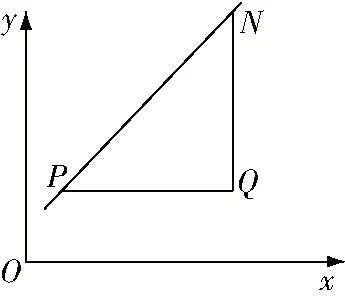
图1
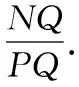
3 类比思想在高中数学解题教学中的应用
3.1 解决数列问题
在高中数学中,数列是很重要的知识点,也是高考的必考点很多学生在解决数列问题时会遇到各种各样的障碍,对此,教师可以引导学生对等差数列、等比数列进行类比,在类比中解决相应的数列问题
已知两个无穷数列{}和{},假设这两个数列都是等比数列,且公比不是-1,对这两个数列进行运算后,可以形成新的数列{+},{},并且得到的新数列也是等比数列,若假设题目中的数列为等差数列,试将等差数列的前项和公式写出,用含有首项和公差的式子进行表示
在这个问题中,学生会出现不知道如何入手的情况对此,教师可以指导学生使用类比思维,观察新数列的公比性质依据已知信息,可以看出是新数列{}的公比,其中,为原来两个数列{},{}的公比之积,其首项为原来两个数列的首项之积;在新数列{+}中,+为首项,根据题目信息可以知道,数列{+}也是等比数列,存在公比,且为原来两个数列的公比之和以此为依据进行类比,可假设两个数列{},{}是等差数列,并且公差分别为,

对其进行分类讨论:

假设题目中的两个数列{},{}的公差都是0,则可以判定数列{}也是等差数列
3.2 解决函数问题
高中数学教师在引导学生解决函数问题时也可以用到类比思想,让学生在类比中寻找函数解题思路,从而提高解题效率
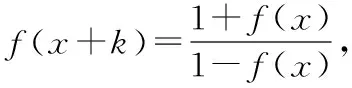
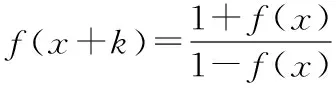
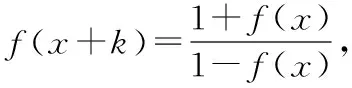
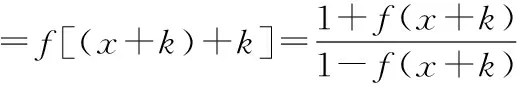
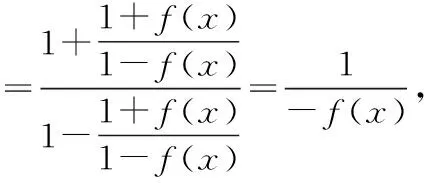
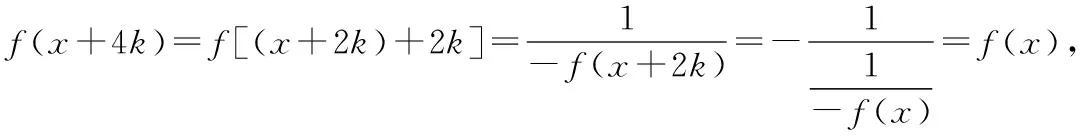
从而证明()是周期函数
3.3 解决代数问题
高中数学教师在日常教学中还可以指导学生通过类比思维解决一些问题,以此促进学习效果的提升
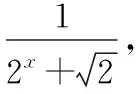
在解决这个问题时,如果学生一个数一个数地求解会很麻烦,并且在解题过程中也可能由于粗心大意而出错对此,教师可以指引学生用类比思维,依据等差数列前项和公式倒序相加,这与等差数列前项和公式推导方法相类比
(-5)+(-4)+(-3)+…+(0)+…+(5)+(6)
=[(-5)+(6)]+[(-4)+(5)]+…+[(0)+(1)],
当+=1时,
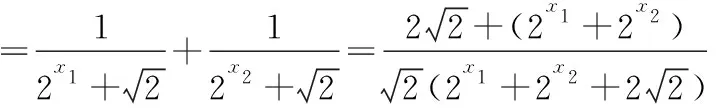
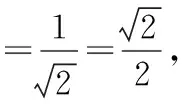
则(-5)+(-4)+(-3)+…+(0)+…+(5)+(6)
=6×[()+()],
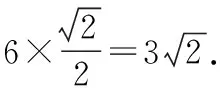
4 高中数学教学中应用类比思想的建议
4.1 构建类比情境
在高中数学教学中,为了更好地增强学生的类比思想,让学生灵活地通过类比思想获取知识,教师可以在课堂教学中为学生构建相应的类比问题情境,引导学生参与体验式学习活动类比问题情境的构建能很好地展示类比推理条件、类比环节、类比过程,也更容易激活学生的学习欲望高中数学教师在课前需要优化课堂设计,认真设计类比问题,并且结合教学目标推进类比思想的渗透,指导学生在类比中深化认知在教学过程中,高中数学教师需要尽可能多地为学生构建一些现实生活中的类比案例,展示类比在生活中的作用,强化学生的类比思维,培养学生的推理能力、分析能力,提高学生的数学思维能力
4.2 开展变式教学
高中数学教师在日常教学过程中还可以开展变式教学,围绕教学目标,改变教学方式、知识展示形式,让学生通过新的方式领悟教师讲解的知识、技能,并从中体会数学学习的乐趣,促进数学学习能力的提高变式教学是提高高中数学教学质量的关键环节,也是应用类比思想的另一种形式教师在变式教学中应指导学生对知识进行分析,提炼数学表象背后的本质内容,开展类比推理分析,强化问题思维,为后续的类比学习提供保障如在空间两平面平行的性质定理中,教师可以指导学生对平面平行的定义、初中阶段学过的线与线平行的性质进行回顾,在此基础上通过类比思想推理两平面平行的性质教师还可借助变式展示,让学生进行观察、分析,形成结论,并通过适宜的方式开展论证,这样不仅能让学生体会到类比学习的乐趣,还能增强学生的探索品质,有助于学生科学思维能力的形成
4.3 关注知识生成及合作交流
对高中生来说,开展类比推理的关键是积累丰富的基础知识,这样才可以在类比中借助原有知识推理出新的内容高中生积累的知识越丰富、越充足,在应用类比思想上就越轻松所以,在日常教学环节中,高中数学教师不能单纯地向学生传授数学解题方法、解题策略,还要充分考虑学生的知识积累、生成情况,引导学生在学习中积累原始知识,并找到原始知识与数学思想方法之间的关联,从而在遇到问题时快速想到相应的思想方法、知识形式,促进学习效率的提高
由于高中生的数学思维存在不完善、不成熟的情况,故类比思想对部分学生来说是比较高的思维活动,他们很难凭借自身能力找出知识、问题的内在关联,实现对问题的处理对此,高中数学教师在课堂上要适时引导学生开展小组合作交流活动,注重小组合理搭配,构建轻松的学习氛围,引导学生参与合作交流,让学生相互交流、展示自己,在合作中共同发现知识的内在联系,强化类比思维
在高中数学教学中,教师还要注意引导学生科学地对待类比思想,在课堂上从培养学生能力的角度入手,对学生的类比思想进行培养,调动学生的学习积极性,让学生在主动探索中掌握类比思想,最大限度地发挥类比思想的作用
5 总 结
综上所述,随着我国现代教育事业的快速发展,各界对高中数学教学的要求也逐渐提高在高中数学教学中,教师要特别注重对传统教学模式的改革创新,以此满足学生的发展需求类比思想是一种比较科学的教育方式,将其应用到高中数学教学活动中,可以全面拓展学生的数学思维,拓宽学生的知识面,构建知识框架,对学生的良好发展有很大帮助
