薄壁复合材料圆筒稳定性模拟分析研究
2022-09-16王旻昱
王旻昱
(天津核工业理化工程研究院,天津 300180)
0 引言
圆柱壳体是高速旋转专用设备中的重要部件,高速运转时承受巨大的旋转载荷,因此圆柱壳需要具有足够大的环向强度,并提供一定的轴向刚度。纤维增强树脂基复合材料具有高比强度、高比刚度、质量轻、抗疲劳性强等优点,目前复合材料圆筒已应用于旋转机械,结构为多层缠绕,包括角度层和环向层[1-4]。对于转速较高的旋转机械,为提高复合材料圆柱壳体的承载能力,圆柱壳成型后需要对筒体施加一定的预应力,以保证高速运转下其强度满足设计要求,如果施加预应力过大可能导致圆柱壳的屈曲失稳,影响整体性能,因此有必要开展复合材料圆柱壳体稳定性的研究。
圆柱壳体的稳定性问题国内外已开展过大量的研究,大部分研究对象为金属壳体,余军昌对圆柱壳体受外力作用下进行有限元分析,并将结果与理论计算值进行比较分析,说明有限元软件可以成为分析容器稳定性的一种方法[4];崔伟通过对多组尺寸薄壁短圆筒进行外压稳定性实验,并利用有限元ANSYS对模型进行分析,分析了模拟值、实验数据值以及理论值三者之间的关系[5]。
上述研究证明了有限元方法对圆柱壳体稳定性分析的适用性。对于复合材料圆筒,材料本身具有各向异性,结构为多角度缠绕铺层,影响因素较多,因此对其稳定性进行解析,分析较为复杂。本文采用有限元方法,通过数值模拟的方法分析复合材料圆柱壳稳定性问题,确定铺层角度、铺层顺序对稳定性的影响规律。
1 计算模型建立
本文利用有限元软件ANSYS进行分析,在Workbench平台中,ACP组件具有全面的复合材料产品设计分析功能,适用于壳模型的分析计算。有限元分析过程主要包括三个步骤:前处理、求解、后处理,本文通过ACP组件进行几何尺寸确定、复合材料定义等前处理流程,再导出到Mechanical模块完成后续有限元分析[6]。
复合材料圆柱壳体直径150 mm,长度500 mm,壁厚2.1 mm。铺层结构包括角度为±α的螺旋缠绕层和环向层,以一定的铺层顺序缠绕成型。材料方面均使用T700级碳纤维复合材料,材料参数在表1中列出。

表1 T700级碳纤维复合材料基础材料参数
利用ACP模块划分网格,定义复合材料过程中确定圆柱坐标系的轴向为铺层参考方向,设定铺层角度。得到铺层结构如图1所示。

图1 圆柱壳铺层结构示意图
根据实际情况定义边界条件,约束壳体两端三个方向的平动位移,对壳体施加一定大小的外压。约束条件的施加如2图所示。

图2 圆柱壳施加约束
2 稳定性分析
圆筒壳体在均布外压的作用下,会受到环向和轴向的压缩应力,存在一个小于材料屈服极限的压应力,使壳体失去原有的形状,形成局部凹陷、局部凸起的波形,这种现象称为壳体的失稳。此时的压应力即为圆筒壳体的屈曲临界载荷。
特征值屈曲分析属于结构线性分析,可用于预测理想线弹性结构的理论屈曲强度。其方程为下式:
([K]+λ[S])[φ]=0
(1)
其中[K]表示刚度矩阵,[S]代表应力刚度矩阵,[φ]表示位移特征矢量,λ表示特征值或载荷因子。上式为线性屈曲的求解方程,λ与载荷F相乘可得到屈曲临界载荷。
2.1 特征值计算结果
对建立的复合材料圆筒模型施加1.5 MPa的外压,通过Block Lanczos方法提取模型的前十阶模态。其特征值见表2。
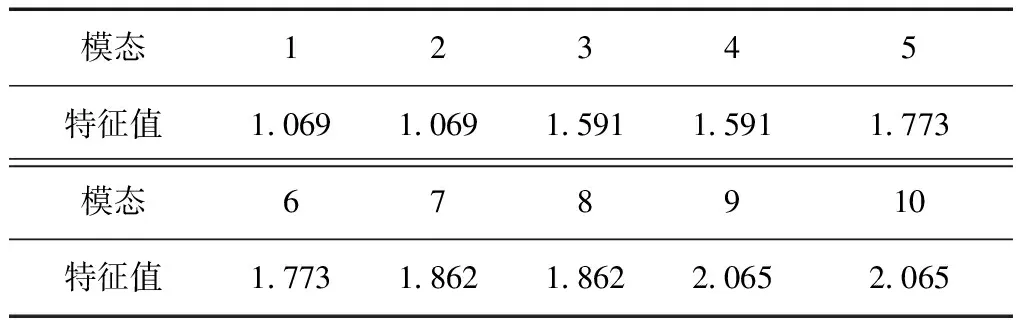
表2 复合材料圆筒前十阶模态特征值
根据计算结果,前十阶模态中每2阶模态特征值相同,图3和图4为前2阶模态图,可以看到2阶模态只是屈曲形态的方向不同。第1阶和第2阶模态的特征值最小,即为圆筒失稳临界压力对应的特征值,计算结果为1.605 MPa,圆筒失稳波数为3。

图3 第1阶模态图
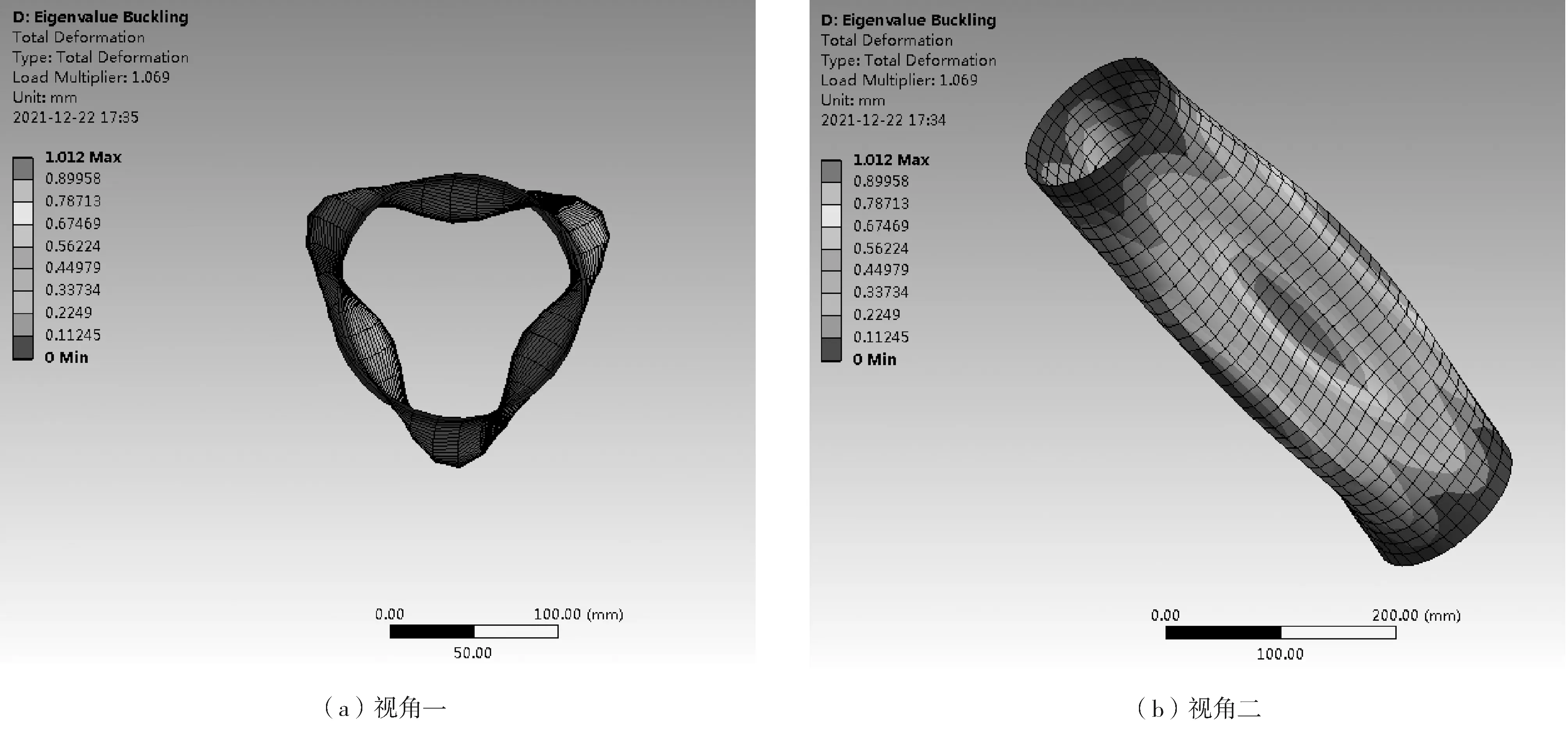
图4 第2阶模态图
2.2 铺层厚度对圆筒临界压力影响
复合材料圆筒总厚度和铺层顺序不变,改变角度层与环向层的厚度比,计算不同铺层厚度对圆筒临界压力的影响,计算结果见表3。绘制环向层与角度层厚度比与临界压力的关系如图5所示。
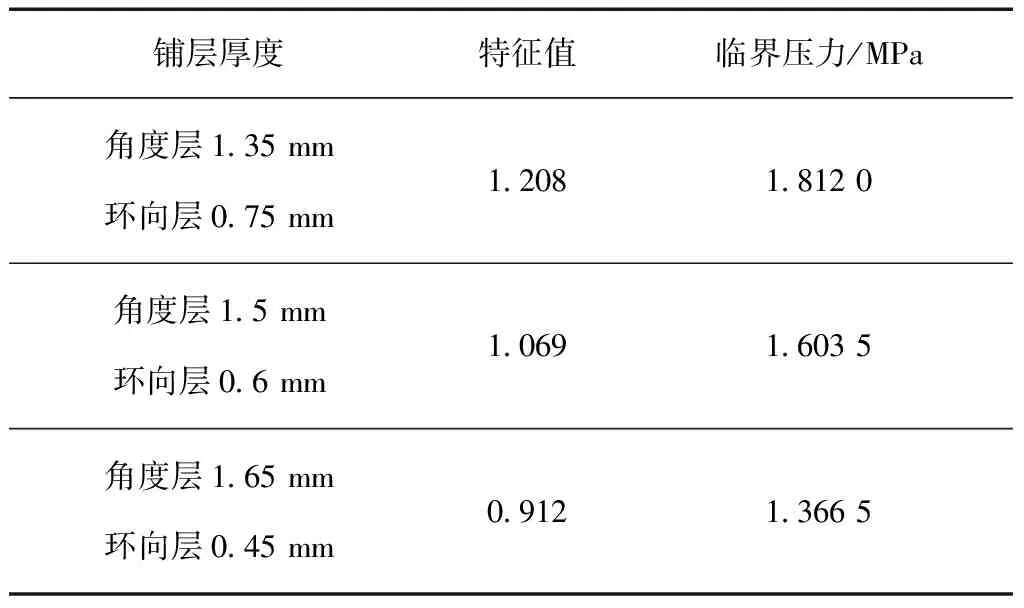
表3 不同铺层厚度圆筒失稳临界压力

图5 铺层厚度比与临界压力关系
根据计算结果,环向层厚度占比越大,复合材料圆筒的失稳临界压力越大,临界压力与环向层、角度层厚度比基本为线性关系。
2.3 铺层角度对圆筒临界压力影响
在复合材料圆筒环向层与角度层厚度和铺层顺序不变的情况下,在65 °~80 °范围内修改复合材料圆筒角度层铺层角度,计算不同铺层角度的复合材料圆筒的失稳临界压力。计算结果见表4。
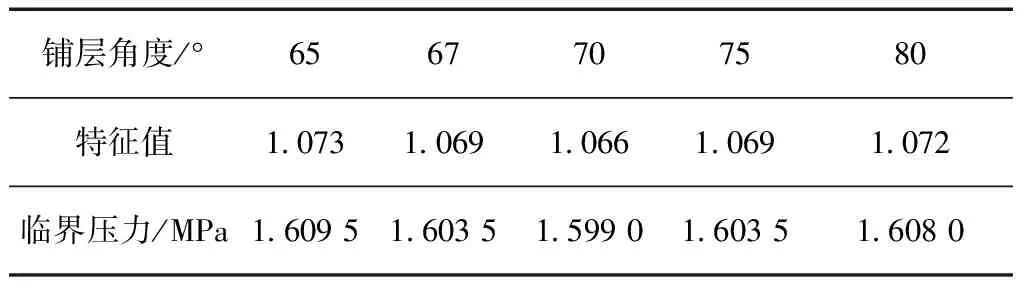
表4 不同铺层角度圆筒失稳临界压力
根据计算结果,在65 °~80 °范围内改变角度层铺层角度,复合材料圆筒的失稳临界压力基本没有变化,数值稳定在1.6 MPa。
2.3 铺层顺序对圆筒临界压力影响
保持环向层与角度层厚度和铺层角度不变,分析环向层和角度层的铺层顺序对圆筒临界压力的影响。复合材料圆筒包括2层角度层和3层环向层,选择了5种不同铺层顺序计算复合材料圆筒的失稳临界压力。计算结果见表5。

表5 不同铺层顺序圆筒失稳临界压力
上述计算表明,环向层与角度层的铺层顺序对复合材料圆筒临界压力影响较大,75 °/0 °/0 °/0 °/75 °铺层临界压力最小,0 °/0 °/75 °/75 °/0 °铺层临界压力最大,最大值约为最小值的3倍。
3 结论
本文采用有限元方法对复合材料圆筒的稳定性问题进行了分析研究,建立有限元壳体模型,通过特征值法计算失稳临界压力,并分析铺层角度、铺层顺序对复合材料圆筒稳定性的影响。得到以下结论:
(1)圆筒失稳临界压力与环向层和角度层的厚度比基本为线性关系,环向层厚度占比越大,复合材料圆筒的失稳临界压力越大。
(2)圆筒的环向层与角度层厚度和铺层顺序不变,在65 °~80 °范围内,改变角度层的缠绕角度对复合材料圆筒的失稳临界压力没有影响。
(3)圆筒的环向层与角度层厚度和铺层角度不变,改变铺层顺序对复合材料圆筒临界压力存在影响,采用不同铺层顺序的圆筒临界压力相差较大。
