新型固体氧化物燃料电池连接件的结构设计与数值仿真

支训廷 ,王家堂 ,苗 鹤* ,尹明明 ,肖柳胜 ,户睿淦 ,袁金良

（1.宁波大学 海运学院,浙江 宁波 315832;2.中国地质大学(武汉) 材料与化学学院,湖北 武汉 430074）

固体氧化物燃料电池(SOFC)是一种将反应气体中的化学能直接转化成电能的装置,具有发电效率高、原料成本低、噪音小等优点,是目前新能源领域研究热点之一[1-2].SOFC 结构主要包括板式和管式.与管式SOFC 相比,板式SOFC 具有功率密度高、结构紧凑等优点,受到广泛关注.其中,连接件是板式SOFC 一个关键部件,其传质面积、反应气体的流速、压力和浓度分布等因素直接影响电池的输出功率.因此,人们通常采用优化连接件结构来增加电池传质面积占比,改善反应气体流速和浓度分布的均匀度,进而提高燃料电池的输出功率.

板式SOFC 连接件的流道主要有平直型、蛇形及离散型等[3-5].文献[6-7]报道了采用变截面平直流道结构可提高电池的功率密度及输出功率.平直流道结构流道设计简单,但容易造成气体分布严重不均,导致SOFC 发电效率下降[8-9].文献[10-11]研究了蛇形结构,发现改变蛇形流场流道尺寸能显著提高电池的平均电流密度.但蛇形流场的流道较长,会造成较大的压降,影响其输出功率[12-13].而离散型流场结构能增强反应气体的扰动,增加反应气体在离散单元所覆盖区域下的渗透量,获得较高的功率密度,因此近几年受到了有关学者的青睐[14-16],其中连接件结构是电池性能优劣的关键.文献[17-18]发现,不连续对称圆柱体结构可提高流场分布的均匀性.文献[19]设计了弯月状凹凸结构,提高了反应气体分布的均匀性.Atyabi 等[20]设计的六棱柱体结构增强了氧气向气体扩散层的传递,提高了电池的传质能力.Li 等[21]使用柱形连接件使电堆在850 ℃时的功率密度提高至0.72 W·cm-2.高祥[22]研究发现,相对于传统连接体,离散式交叉形连接件结构使SOFC 电池堆输出电流密度增加了20.6%.但在电池的传质能力、电流密度等方面还存在一些问题,如不合理的离散结构会使反应气体产生涡流,导致燃料发生短路;较小的压降会影响电池的扩散传质能力.

针对上述问题,本文提出一种新型的离散型连接件结构,即A 型连接件(由若干等腰三角形区域组成,而且等腰三角形区域交错布置).采用COMSOL Multiphysics 数值模拟仿真平台,模拟了由A型连接件构成的三维SOFC性能,分析了电池模型的气体速度场、气体压力场、气体浓度场对电池性能的影响,改进了离散体形状与布置方式,优化了流场的均匀性,提高了反应气体的利用率.与平直流道型连接件(B 型连接件)对比发现,A 型连接件电池堆的最大输出功率提升了61.27%,这可为提升电池性能提供参考.

1 数值模型

1.1 几何模型和参数

本研究建立的A 型和B 型连接件的几何结构和尺寸如图1 所示.模型分别由电解质、多孔气体扩散电极和气体流道组成,电解质在阴极和阳极之间,形成“三明治”结构.

图1 SOFC 电池的几何模型

工作条件下数值模型求解方程主要包括动量、质量、能量、电荷等控制方程,以及Nernst、Butler-Volmer、交换电流密度、欧姆定律等电化学反应方程[23-26].

物质传递控制方程为:

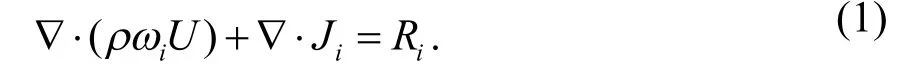
反应气体虽然在电极上持续反应,但总物质质量保持守恒.守恒方程为:

能量守恒控制方程为:

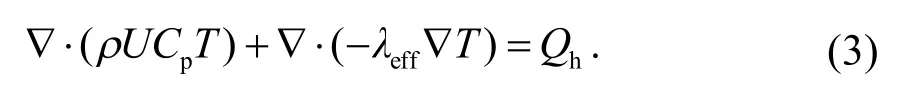
电荷守恒方程为:

式中: ∇是哈密顿算子,表示该物理量的梯度;ρ是混合气体密度,kg·m-3;ωi是气体i的质量分数;U是流速,m·s-1;Ji是气体i的扩散通量,kg·(m2·s)-1;Ri是气体i在电化学反应中消耗速度或生成速度,kg·(m3·s)-1;Qbr是气体质量源项,kg·(m3·s)-1;Qh是电池运行各类热量的总和,W·m-3;Cp是气体定压比热容,J·(kg·K)-1;λeff是导热系数,W·(m·K)-1;和为电子和离子有效电导率,S·m-1;φelec和φion为随着反应进行所形成的电子电势和离子电势,V;Sa为发生反应的活性比表面积,m2·g-1;E0是理想电池电压,V;P是气体分压,P0是标准大气压;R是摩尔气体常数;T是绝对温度;F是法拉第常数;ne为反应发生时所迁移的电子数;i是电流密度,A·m-2;i0是交换电流密度,A·m-2;ηact是活化极化损耗;β是传输系数;iloc,a是阳极局部电流密度,A·m-2;i0,a是阳极交换电流密度,A·m-2;CR是原物质影响系数;CO是氧化物质影响系数;η是活化极化过电位;是阴极传递系数;是阳极传递系数;iv,c是阴极局部电流密度,A·m-2;av是活性比表面积;i0,c是阴极交换电流密度,A·m-2;为电池中的阴极气体流道;CO2,ref为氧化物质的参考影响系数;Ct为电池运行温度的影响系数.

数值模型所涉及的主要物理参数为[23-26]:i0,a为1166.2 A·m-2;i0,c为4 637.4 A·m-2;av为102 500 m2·g-1;阳极对电子有效传导系数为2 149.2 S·m-1;阴极对电子有效传导系数为5 093 S·m-1;阳极对离子有效传导系数为2.266 9 S·m-1;阴极对离子有效传导系数为2.266 9 S·m-1;电解质对离子有效传导系数为2.266 9 S·m-1;连接件对电子有效传导系数为310.93 S·m-1;H2-H2O 扩散系数为8.5×10-4m2·s-1;O2-H2O 扩散系数为2.45×10-4m2·s-1;O2-N2扩散系数为1.92×10-4m2·s-1;N2-H2O 扩散系数为2.45×10-4m2·s-1;孔隙率为0.4;β为0.5;为2;为1.5;阳极出口压力和阴极出口压力均为0.

假设数值模型反应气体均为不可压缩的理想气体,多孔电极的材质均匀且各向同性,电池内部的气体流动均为层流流动.电池工作在恒定温度800 ℃.电池采用氢气和空气作为阳极和阴极的入口气体,气体压力设置在流道出口处,即背压方式.

1.2 模型验证

对所建立的A 模型进行网格无关性和科学性验证.通过减少和增加网格数测试网格的独立性.采用862 410、727 330、60 260、530 400、47 680个网格用COMSOL Multiphysics 软件模拟计算模型A,在0.8 V 电压下得到电流密度分别为9 020.5、9 019.8、9 018.6、9 014.2、9 012.1 A·m-2共5 个模型的电池输出功率密度误差小于1%.选择网格数为530 400 时既能确保计算精度,又能减少模拟计算量.因此,以下计算中模型A 和B 均采用530 400个网格.为了验证数值模型的科学性,模型A 采用与文献[18]中相同参数,结果对比如图2 所示.数值计算结果与实验测量结果之间的误差小于1%,说明本文采用的数值分析方法可靠.

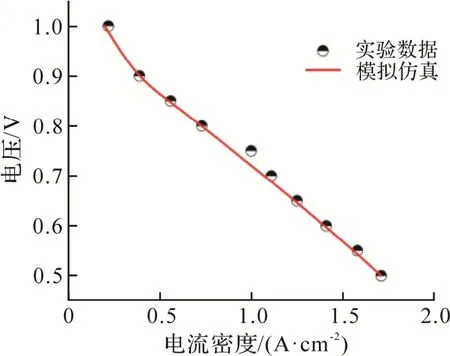
图2 数值计算与实验数据对比结果[18]

2 结果与讨论

2.1 气体速度场对比

图3 为流道内速度场分布.由于流动阻力和气体本身的扩散特性,流道中反应气体在流动过程中逐渐减少.当反应气体达到多孔电极扩散层时,受电极低渗透率影响,反应气体速度场迅速减小.同时,气体本身的黏性系数也会影响气流分布,在流道壁面形成边界层,流动中心的流速比周围靠近壁面的流速大,最终导致反应气体到达电极扩散层壁面时流速很小.

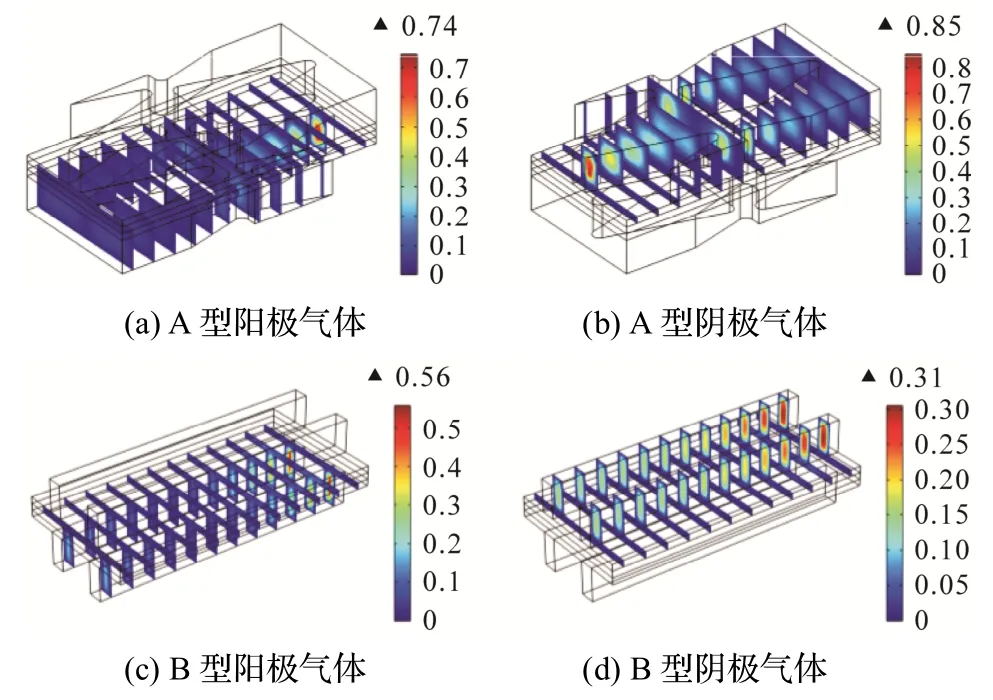
图3 A 型与B 型气体流速场分布(单位: m·s-1)

图4 是2 种连接件所构成电池的气体速度场对比.从图4 可知,A 型连接件阳极流道气体的最大流速为0.74 m·s-1,大于B 型连接件的最大流速(0.56 m·s-1);阴极流道气体的最大流速为0.85 m·s-1,大于B 型连接件的最大流速(0.31 m·s-1).A 型连接件流道的尺寸先增后减再增,往复变化,因此形成气体流道截面规律性渐变,导致流道内阳极气体流速呈现先增后减再增的趋势;而阴极流速呈现先减后增再减的趋势.表明A 型连接件阳极和阴极流道气体均具有较大的流速,有利于提高反应气体的传质能力,提升电池性能.

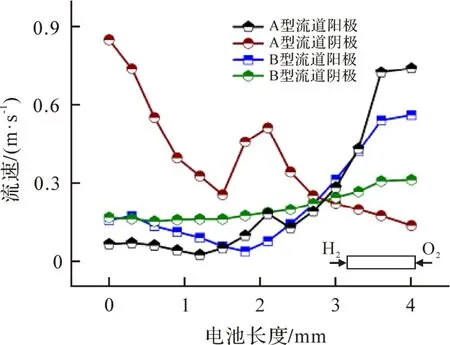
图4 A 型与B 型连接件气体流速场对比

2.2 气体压力场对比

燃料电池工作时,反应气体需足够压力才能保证反应气体的流速,提高反应速率.不同结构连接件的流动阻力不同,不同流道设计模式下实际阻力存在一定差异.当流道内产生较大压降时,空压机的功率增加,功率损耗随之增加,导致燃料电池整体性能降低.流道进出口压降可反映流道流阻大小.图5 为2 种连接件流道气体的压力分布.

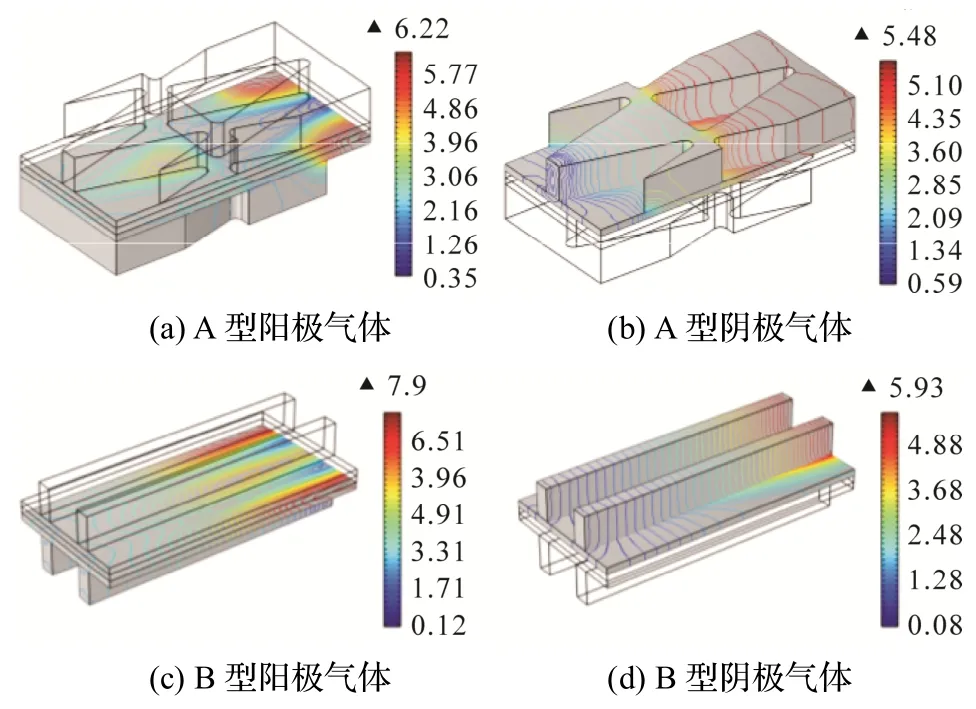
图5 A 型与B 型连接件气体压力场分布(单位: Pa)

图6 是2 种连接件电池气体压力场对比.从图6 可知,在流道内部沿着气体行进方向流道压力不断下降,A 型连接件阳极流道压降为5.87 Pa,阴极流道压降为4.89 Pa.B 型连接件阳极流道压降为7.78 Pa,阴极流道压降为5.85 Pa.A 型连接件的阳极和阴极流道压降均低于B型连接件,说明A型连接件气体流道的阻力较小,更有利于气体的流动,可减小空压机的功率损耗,提升燃料电池的性能.

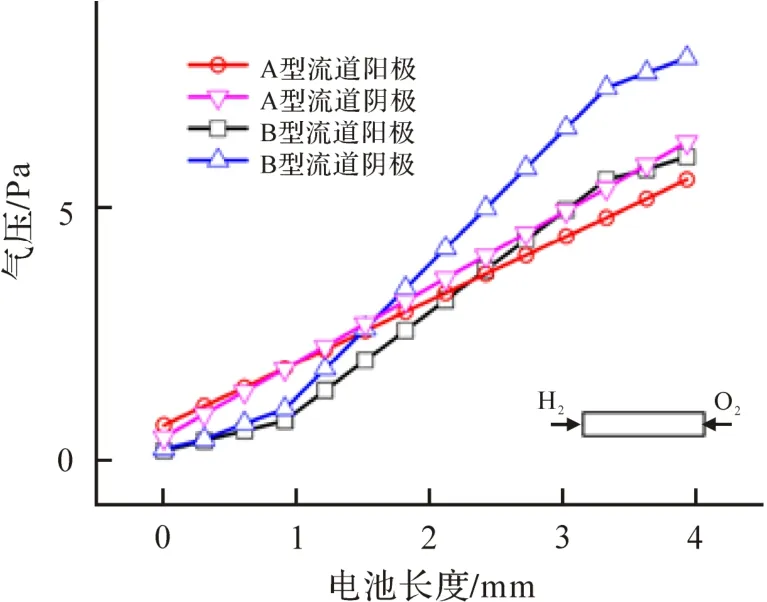
图6 A 型与B 型的气体压力场对比

2.3 气体浓度场对比

在固体氧化物燃料电池中,氧气浓度在进气口前半部分迅速下降,之后速度趋于平缓.这主要是因为随着反应进行阴极流道中氧气摩尔分数变化速率随之加快.据化学动力学可知,化学反应速率与反应物浓度成正比.当氧气消耗后,浓度下降,其反应速率随之变慢,氧气消耗速度会减小.对于氢气,燃料入口附近的氢气浓度大,阳极处的反应速度大于阴极处.据反应动力学原理,当氢气浓度下降时,其反应速率随之变慢,氢气消耗速度减小.

图7 是2 种连接件所构成电池的气体浓度场分布.从图7 可发现,A 型连接件流道区域显示高浓度状态,且浓度分布比较均匀.

图7 A 型与B 型连接件气体浓度场分布

图8 是2 种连接件所构成电池的气体浓度场对比.从图8 可知,A 型连接件阴极和阳极的气体浓度变化较为缓慢,说明A型连接件流道比B型显示出更强的传质能力.

图8 A 型与B 型连接件气体浓度场对比

2.4 电池输出电流、电压及功率性能对比

在电池运行过程中,输出功率作为反映SOFC工作性能的重要参数,直接反映了SOFC 的输出能力和工作稳定性.电池的输出功率主要取决于电流密度,其本质是电化学反应速率.反应气体的浓度分布是影响电流密度的关键因素.

图9 为2 种连接件所构成电池在不同电压下电流密度和输出功率.

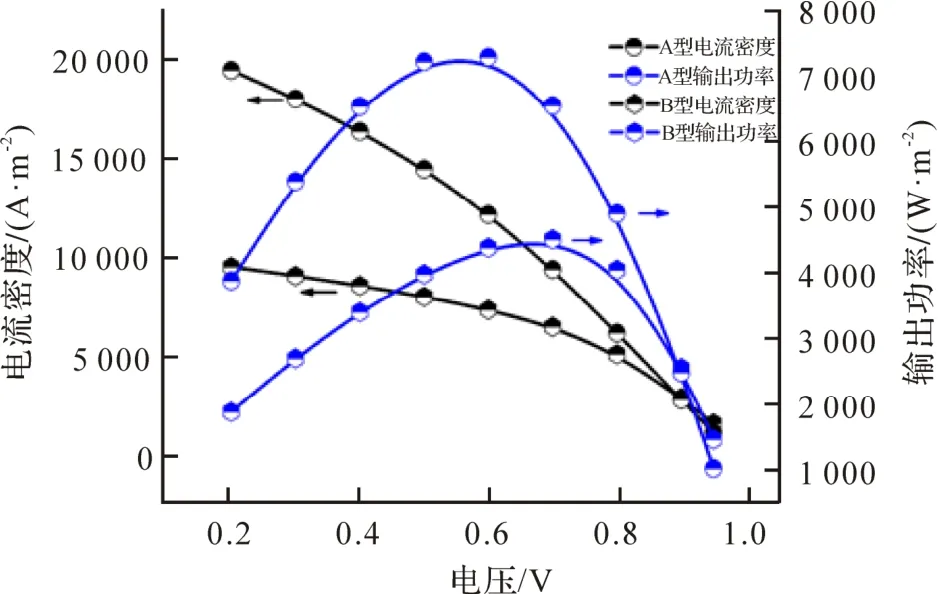
图9 A 型与B 型电流、电压及功率性能对比

从图9 可知,2 种连接件呈现出相同的变化趋势.随着电压增大,电流密度均随之减小,输出功率先增后减;A 型连接件电池的最大电流密度为19 389.253 A·m-2,B 型连接件电池的最大电流密度为9 466.127 A·m-2;A 型连接件电池的最大输出功率为7 267.09 W·m-2,B型连接件电池的最大输出功率为4 506.11W·m-2.与B 型相比,A 型的最大输出功率提高了61.27%.

3 结语

本文设计了一种由等腰三角形区域交错布置而成的A 型离散连接件,对该连接件构成的电池模型进行了数值模拟,并与平直流道型连接件进行比较.结果发现,A 型离散连接件构成的电池模型流道内的气体流速较大,反应气体分布更均匀,具有更强的传质能力.采用A 型离散连接件的电池模型的阳极气体流速约为平直流道型连接件电池模型的1.32 倍,阴极气体流速约为2.74 倍,最大输出功率提升了61.27%.