工业物联网中基于SMDP的协同卸载方案
2022-09-16赵尚维康
赵尚维康,孙 君
(南京邮电大学 江苏省无线通信实验室,江苏 南京 210003)
0 引 言
近些年来,工业物联网(IIoT)作为一种新的范式,在无线通信和微电子领域得到了广泛的关注。工业物联网连接了大量移动数字设备、制造机器、工业设备等,这些设备不断产生大量的数据和信号,用于传感、控制、系统维护和数据分析[1]。与此同时,由于现代智能设备对网络时延要求越来越高[2],边缘计算技术受到了广泛的关注[3]。边缘计算技术的基本思想是将云网络中的一些用户面功能下沉到网络边缘靠近用户的边缘节点,当用户访问网络中的一些基本功能时,访问和回传信息所经历的传输路径更短,从而降低时延[4-6]。为了将一部分工业应用任务卸载到具有足够计算资源的计算系统上执行[7],该文在工业物联网系统中引入边缘计算,利用多接入边缘计算(MEC)服务器强大的CPU处理器为密集的计算任务提供算力支持。由于MEC服务器计算资源有限,这种方案需要考虑计算任务卸载和资源分配的决策问题。
关于计算任务卸载和资源分配决策问题,国内外研究学者提出过多种算法。例如文献[8]中提出基于交替方向乘子法(ADMM)框架,将卸载决策、频谱分配、计算资源分配和缓存决策作为优化变量,然后采用拉格朗日乘子迭代的方式找到分配决策问题的最优解[9-11]。文献[12-14]中提出了与之类似的衍生算法,考虑了扩展计算卸载决策的范围,做卸载决策优化时考虑了MEC之间进行任务卸载的水平协作。但这些方法存在缺陷,采用拉格朗日迭代法进行系统决策优化的算法复杂度过高,且由于引入了二进制变量的决策行为,这一操作会导致额外的损失。文献[15]提出了通过遗传算法对决策事件集不断进行交叉变换和突变操作来得到最优解的方法。但缺点是资源利用率改善不大。除此之外,一些学者把系统决策过程建模为马尔可夫决策过程,利用马尔可夫状态转移的模型逐步迭代找到最优解。比如文献[16]在移动边缘计算环境中,把系统中目前被占用的计算资源量建模为状态空间,在多个UE之间决定是否在MEC上执行卸载任务。文献[17]中同时考虑正在执行的计算任务数,扩充了系统状态空间和可能发生的事件空间。但这些方法未考虑与周围MEC服务器的协作问题。文献[18]将M/M/s排队模型运用于计算任务卸载中,把多个MEC服务器的计算资源联合分配,但这种分配过程系统性能的随机性太高。文献[19]在M个MEC服务器联合进行计算任务的卸载模型下提出了最小负载卸载算法,但仅考虑了对系统卸载成功率的改善,忽略了计算任务卸载过程中对于其他性能的提升。文献[20]在集群化MEC网络中提出基于模拟退火算法的分配算法,其以最小化业务请求的传播时延为目标将M个MEC服务器中的虚拟资源联合分配,但该算法忽略了集群MEC网络中计算任务在MEC服务器中的传输时延对系统性能的影响,实际上,在IIoT这类对时延极其敏感的场景,该时延往往不可忽视。
为解决以上所提问题,该文研究了IIoT场景下系统时延和能耗总收益最大化的资源分配问题。
1 系统模型与问题建模
1.1 系统描述
图1描述了一个典型的IIoT系统,该系统由小区基站、小区中架设的MEC服务器和众多工业设备组成。IIoT系统中,当工业设备产生了计算请求时,设备可以将计算任务卸载到部署了MEC服务器的网络边缘接入点,由MEC服务器对任务进行处理,同时,由于MEC服务器之间通过有线链路连接,MEC之间的数据往返传输时间极短,MEC之间可以共享有限的计算资源。
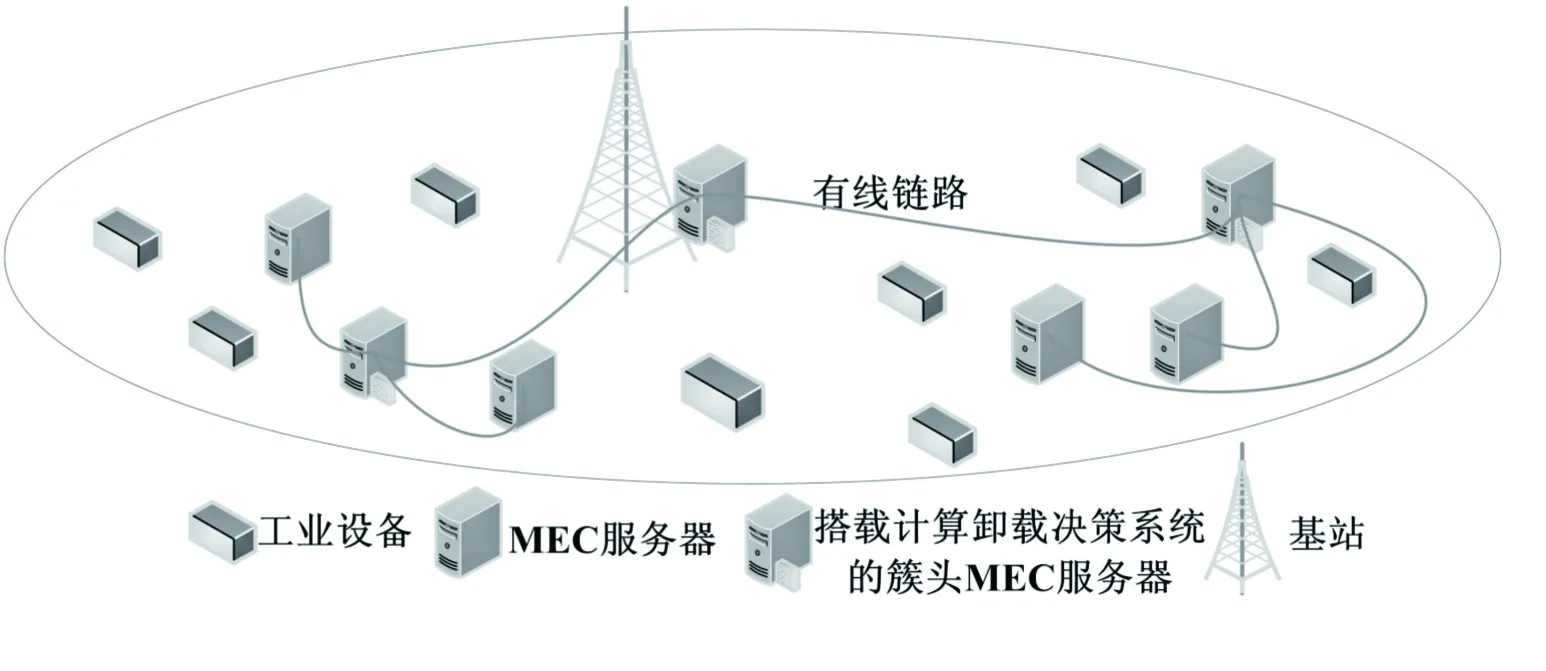
图1 系统部署场景
基于上述分析,在小区内架设N个MEC服务器。通过网络功能虚拟化(NFV)技术把MEC中的计算资源虚拟集成为若干个RU。该文假设每个MEC服务器拥有M个计算能力相同的RU。计算任务服务请求的速率可视为服从参数为λp的泊松分布,MEC服务器所拥有的RU处理完成计算任务的速率可视为服从参数为μp的指数分布[16]。
为提高MEC系统的资源利用率并利用MEC系统内的有线链路缩短数据往返的传输时间,把小区中的MEC服务器按照地理位置聚类为若干个簇,将相邻的L个MEC服务器聚类为一个簇,且将这L个MEC服务器中距离其他各MEC服务器距离之和最短的MEC服务器定义为簇的头部,由其充当控制单元执行决策算法的计算并把优化决策传递到簇内各个成员。。
1.2 基于SMDP的协同卸载系统
该系统采取决策的过程,实质上是通过分析簇内计算资源信息然后选择使系统获得最大效益的行为。这是一个序列决策问题,这一问题很适合采用机器学习中的强化学习(RL)来解决。在无线通信传输系统中,马尔可夫决策过程(MDP)是在随机控制过程中对智能体建模的经典方法。在IIoT这类场景设备请求计算任务卸载的行为可视为一个半马尔可夫过程[16]。SMDP正适合解决这类两次决策间隔时间是连续且为独立同分布随机变量的决策问题。
处理SMDP问题需要分析系统的状态空间、行为空间、奖励函数和转移概率。该文将MEC服务器内计算资源被占用的情况定义为系统的状态空间,将一事件发生时系统所采取的卸载行为定义为行为空间,根据系统处理计算任务的时间和成本定义奖励函数,通过分析系统的状态空间和行为空间可以得出系统内的状态转移概率。下文将对SMDP的这四个关键要素进行详尽的描述和分析。
1.2.1 状态空间
状态空间反映簇内的计算资源信息与系统当前的情况,是系统选择决策行为的重要依据。该文以簇内每个MEC服务器内计算资源被占用的情况为依据定义状态空间S。状态空间中参数事件e表示接下来到来的事件,系统需要根据当前状态下发生的事件来进行决策。综上,定义的状态空间为:
S={s|s=(k1,k2,…,km,…,kL,e)}
(1)
其中,符号km,m∈[1,L]为簇中序号为m的MEC已被占用的RU数,km≤M,符号M为MEC所拥有的RU的最大数量,符号L为该MEC簇的大小,用该参数来表征计算资源被占用的情况。
其中的事件e表示为:
e∈ε={A1,A2,…,Ai,…,AL,
D1,D2,…,Dj,…,DL}
(2)
其中,符号Ai,i∈[1,L]用于描述簇内序号为i的MEC服务器的服务范围内是否产生了卸载服务的请求,符号Dj,j∈[1,L]表示序号为j的MEC内一项计算任务完成并释放了一个RU单元。
1.2.2 行为空间
当一个事件发生时,系统需要依据当前的状态和发生的事件做出决策行为,系统中所有可以被采取的决策行为a包含于行为空间A中。
A={-1,0,1,2,…,m,…,L}
(3)
其中,A=-1表示此时一项计算任务完成并成功释放计算资源空间;A=m表示将当前到来的计算任务卸载请求卸载到第m个MEC服务器进行处理,通过任务分解技术可以统一分配一个RU进行任务处理;A=0表示拒绝当前到来的计算任务卸载请求。
1.2.3 奖励函数
奖励函数是系统在当前状态下采取某一确定行为的回报值。该文定义利润函数为采取当前行为所减少的系统处理计算任务所耗费的时间。此外簇内的计算资源被使用会带来额外的成本,一旦簇内MEC服务器的计算资源被使用,在计算资源被占用的时间内都会产生电力成本和MEC服务器硬件的维护成本,这一成本的大小与计算资源被占用的情况有关。
因此对于一个给定的行为a,奖励函数为:
r(s,a)=k(s,a)-g(s,a)
(4)
其中,
k(s,a)=
(5)
其中,
(6)
符号k(s,a)表示状态s下采取行为a得到的利润,其反映了采取行为A=m所减少的系统处理该计算任务所耗费的时间,符号βd为减少的耗费时间的单位利润,符号T为设备本地处理该计算任务的单位时间,符号δ1为两个相邻MEC间传递最小任务单元的传输时延,|m-i|δ1表示计算任务从簇内第m个MEC传输到第i个MEC所花费的传输时间,符号g(s,a)为维持状态s的成本,由状态s下的计算资源占用率和事件持续时间联合决定。符号βe为MEC在单位时间内产生的单位损耗成本,符号τ(s,a)为当前状态s内事件e的持续时间,为前一状态到后一状态的间隔时间,该间隔时间服从指数分布,其期望为:
(7)
其中,符号α为连续时间折扣因子,符号σ(s,a)为事件发生率,其值:
(8)
通过奖励函数,协同卸载决策系统可以分析得出当前状态下的最佳行为。
2 问题求解
2.1 协同卸载决策的状态转移
事件发生会引起状态的转移,状态转移取决于系统当前状态s和当前采取的行为策略a。下文按照发生的事件e的不同对它们的状态转移过程分别进行讨论。
(1)若s状态下发生的事件为一个计算任务卸载请求到来时,当前状态s可以表示为:
s={s|s=(k1,k2,…,kL,e=Ai)}
(9)
该文用符号s'来表示状态s经过行为a后下一状态,并定义从s到s'的转移概率为P(s'|s,a)。当一个计算任务卸载请求到来时,若接受该计算任务卸载请求,簇内计算资源需要被分配给计算任务,系统状态会发生相应变化,此外,由于系统状态的变化,下一时刻事件发生的概率也会发生变化,由σ(s,a)→σ'(s,a),
(10)
下一时刻的发生事件率分别代表了下一时刻事件e∈{A1,A2,…,AL}到来的速率和事件e∈{D1,D2,…,DL}到来的速率,通过以上分析,可以得到以下转移概率矩阵:
P(s'|s,a)=
(11)
(2)若s状态下发生的事件为一个被卸载的计算任务完成时,与上述分析同理,当前状态s下转移概率可以通过以下转移概率矩阵计算:
P(s'|s,a)=
(12)
2.2 折扣奖励模型
对于一个确定的策略π:S→A,借助奖励函数基于长期效益期望定义了状态值函数。
(13)
式(13)可以通过贝尔曼方程(Bellman Equation)转化为下式[17]:
(14)
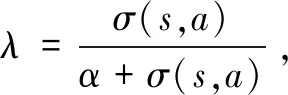
2.3 决策系统的迭代求解
由于贝尔曼方程中可迭代项s与s'的存在,计算任务卸载的决策子问题中具有公共的子子问题,因此该文采用动态规划中的值迭代算法来进行卸载决策的优化,避免了重叠子子问题中不必要的计算工作。详细的描述如下:
算法1:状态值迭代算法。
输入:系统状态集S,系统行动集A,转移概率矩阵P(s'|s,a),收益函数r(s,a),收敛系数ε>0,迭代次数k
输出:最佳策略集π*
1:初始化:对于S中每一个状态s,v(s)→0,k=0
2: while‖vk+1(s)-vk(s)‖>ε
3: forsinS
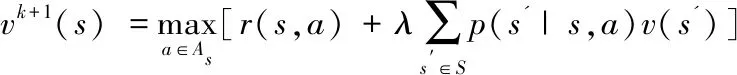
5:k=k+1
7: end
8: end
9: forsinS
11: end
基于平均收益模型,可以得到系统的平均效益函数[17]:
(15)
通过值迭代算法,可以得到状态值收敛后系统采取的最佳策略π*,通过π*,就可以得到系统最佳效益:
g*=gπ*
(16)
3 仿真分析
对所提的基于SMDP的协同卸载算法基于Python平台进行了仿真实验。仿真主要参数见表1。仿真实验中将所提算法与最小负载算法[19]、模拟退火算法[20]进行了比较,仿真对比了这些卸载决策算法下的拒绝服务率和平均效益。

表1 仿真主要参数设置
图2展示了不同计算任务卸载请求速率λp下三种算法在拒绝服务率和系统效益上的性能,其他相关参数μp=4,M=8,L=5保持不变。
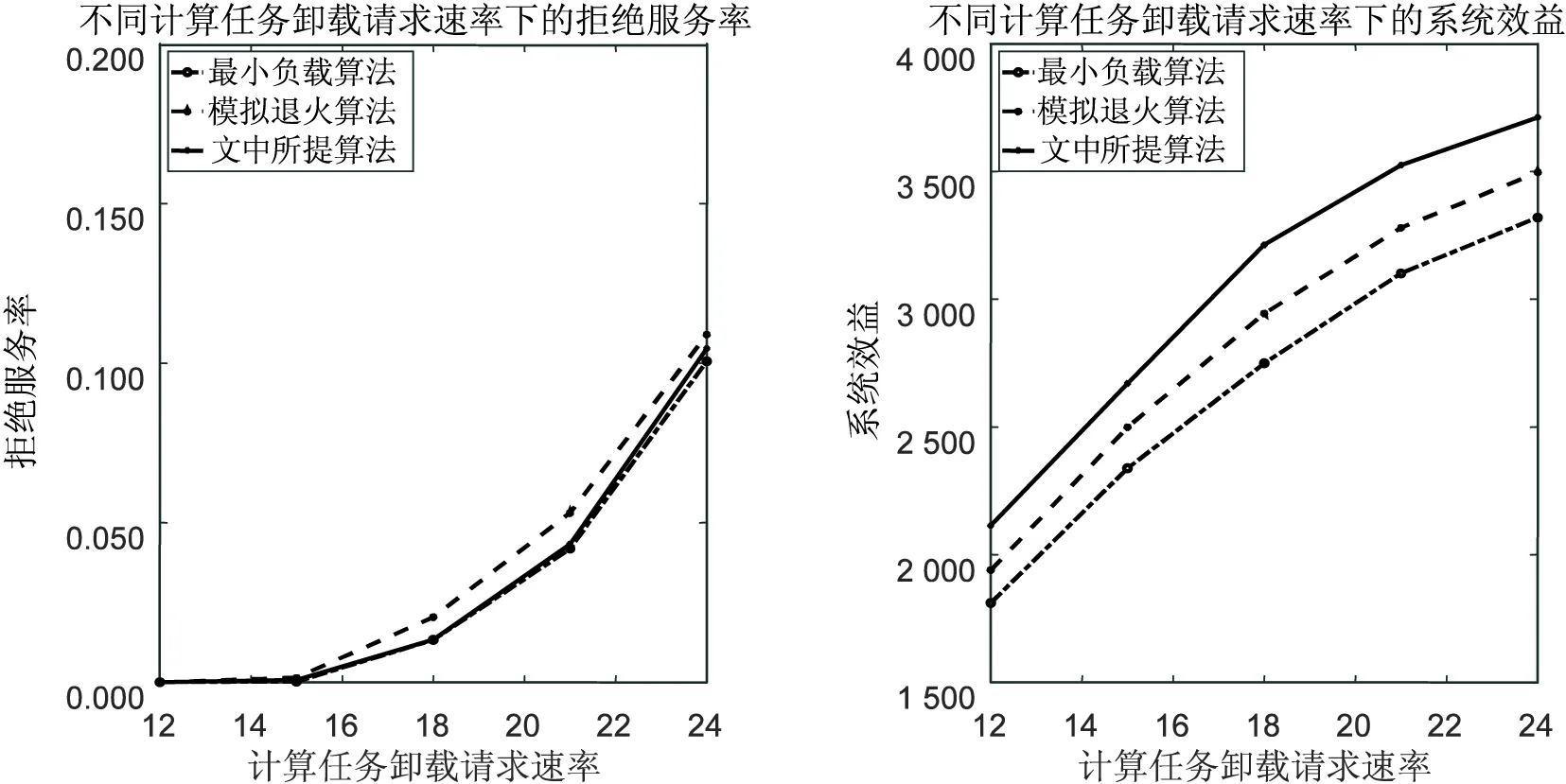
图2 不同计算任务卸载请求速率下的拒绝服务率和系统效益
将三种算法纵向对比可以发现,最小负载算法在拒绝服务率上表现不错,但从系统效益图可以看到相对其他两种算法其决策所产生的系统平均效益并不显著,与之对比,模拟退火算法拥有最糟糕的拒绝服务率,而所提出的基于SMDP的算法缓解了模拟退火算法的高拒绝服务率,且在系统效益上展示出了相对卓越的性能。
图3展示了不同协同MEC数量L下三种算法在拒绝服务率和系统效益上的性能,其他相关参数λp=20,μp=4,M=8保持不变。

图3 不同协同MEC数量下的拒绝服务率和系统效益
将三种算法纵向对比可以发现,L=3时,所提出的SMDP算法拒绝服务率偏高,但随着L数量的提升,所提基于SMDP的决策算法的拒绝服务率逐渐收敛,L=6时,所提算法与最小负载算法相差无几,从系统效益图可以看到,基于SMDP的卸载算法相比于其他两种算法明显取得了更高的系统效益。
4 结束语
针对IIoT系统中计算资源紧缺的问题,在IIoT系统中引入了边缘计算技术,提出一种基于SMDP的协同卸载模型。仿真通过与最小负载算法、模拟退火算法对比表明,所提出的基于SMDP的方案优化了系统拒绝服务率和系统效益的折中、获得了系统性能的显著提升。
