基于信息熵的多Agent 协同观测轨迹优化方法*

夏琪琪，杨惠珍*，王 越

（1.西北工业大学航海学院，西安 710072；2.水下信息与控制重点实验室，西安 710072）

0 引言

多智能体系统协同观测是指多智能体对一个移动目标进行跟踪，每个智能体利用搭载的传感器探测目标，得到目标观测信息，通过融合多个智能体的目标观测值，从而得到更准确的目标状态估值。对于自主水下航行器等类型的智能体来说，传感器固装在智能体上，随着智能体的移动而移动，进而改变智能体对目标的探测，因此，探测与智能体的航迹变化是耦合的。

基于探测与航迹耦合的现象，协调设计目标跟踪滤波器和航迹控制器是一种解决手段。文献［3］以Fisher 信息矩阵（fisher information matrix，FIM）行列式为目标函数，优化平台运动方向，从而获得目标状态估计的最小不确定性。文献［4］提出类似的信息论方法，以互信息为目标函数，将最优观测运动问题建模成部分可观马尔科夫过程，并给出基于最优剪枝的求解方法。文献［5］在研究协同搜索问题时，以最大化平台信息收益为目的，采用分布式求解框架优化无人机（unmanned aerial vehicle，UAV）运动行为。文献［6］针对移动目标估计问题，为了最大化互信息，提高估计精度，设计了仅有方位角测量的多机器人协同导引方法。文献［7］以目标位置协方差矩阵行列式为目标函数，采用梯度下降法对基于测向测距组合传感器的多平台观测轨迹进行设计。文献［8］在文献［7］的基础上，考虑了多平台之间对目标状态估计的一致性问题，引入一致性估计方法对目标状态进行分布式估计，在此基础上，再采用梯度下降法对UAV 运动轨迹进行优化。但由于没有考虑平台的运动学约束问题，所采用的梯度下降法易陷入局部最小点。文献［9］设计了一种基于预测信息的在线航迹规划，将滚动时域与遗传算法结合起来优化航行器轨迹。文献［10］引入条件熵，设计了一种基于传感器和运动概率模型的滚动时域最优控制，通过分析效用函数的结构来减少计算量，但未考虑对状态估计的性能评价。文献［11］研究了基于信息熵的多UAV 目标跟踪控制方法，采用滚动时域优化（receding horizon optimal，RHO）的方法求解最优控制量。本课题组将编队运动和队形设计分开考虑，以FIM 矩阵行列式为目标函数优化多智能体的编队队形，并设计控制器控制智能体按照最优队形运动，从而获得最优的目标状态估计。

本文针对此问题，研究了一种基于信息熵的轨迹优化算法，通过优化信息熵来求解每个智能体的最优角速率控制量，使得多智能体在跟踪移动目标过程中沿着优化的航迹运动，从而获得最优的目标状态估计。

1 问题描述

假设有N 个移动智能体，每个智能体装载被动式传感器，仅能探测到移动目标的方位信息，智能体间共享目标信息进行协同探测。如图1 所示，智能体用三角形表示，目标T 用圆形表示。其中，p表示智能体j 在二维平面的位置，φ为第j 个智能体的速度方向，θ代表智能体j 的传感器探测目标得到的方位信息。期望对多个智能体的轨迹进行优化，从而获得最优的目标状态估计。下面分别对多智能体和目标组成的系统进行分析并建立相应的数学模型。

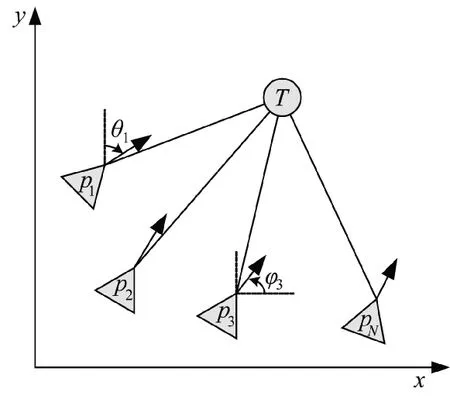
图1 基于纯方位信息的多智能体目标跟踪示意图

1.1 移动智能体运动模型

1.2 目标运动模型

常见的目标运动模型主要有匀速运动和角速度恒定的常速转弯运动。利用这些模型获得的信息作为系统所能得到的关于目标运动的先验信息，在此基础上结合智能体所携带的传感器对目标进行定位，将获得相对方位角信息作为后验信息，从而获得目标的运动状态信息。

目标运动的数学模型为：

1.3 传感器观测模型

假设在k 时刻，第j 个智能体的传感器可以获得对目标方位角的测量值为：

2 基于UIF 的集中式目标状态融合估计

无色信息滤波算法（unscented information filter，UIF）通过在EIF（扩展卡尔曼信息滤波）结构中嵌入一种无色变换方法实现，该方法源于sigma 点滤波器，其中包括无迹卡尔曼滤波（UKF）算法。UIF 的滤波步骤可以参照文献［13］，此处仅列出相关信息计算的步骤。第j 个传感器对目标信息状态向量和信息矩阵的预测方程为：

图2 集中式融合示意图

3 基于信息熵的目标状态估计性能指标函数

3.1 信息熵的概念

由以上公式可知，条件熵的含义为在随机变量已知的条件下，随机变量G 的不确定性；而互信息是随机变量G 包含随机变量F 信息量的度量，也是在给定随机变量F 知识的条件下，原随机变量G 不确定度的缩减量。在滤波跟踪领域，互信息主要用来描述取得观测值后，目标状态估计值不确定性的减小量。因此，在本文中，为了更好地对目标状态进行估计，选取互信息作为优化评价指标。

3.2 基于互信息的优化指标函数

由式（22）可以看出，最大化互信息等同于最大化Fisher 信息矩阵的行列式。随着估计误差的收敛，导致阵的行列式数量级很大，不利于比较。由于信息在数据融合过程中会丢失部分内容，而互信息可以为融合滤波的评估过程和贡献提供评价标准，因此，本文基于互信息来确立优化指标，由于C 为常数，故定义目标跟踪系统的优化指标函数为：

4 基于滚动时域优化的协同观测轨迹优化算法

滚动时域优化（RHO）方法是一种在滚动时域内实时计算最优控制的预测控制方法，由于对模型精度要求不高和具有强鲁棒性等特点，被广泛地应用于各种领域。RHO 方法通过设计代价函数，将状态估计问题转换为带约束的有限时域优化问题，利用有限时域内采集的信息估计目标状态，能够有效地解决实时决策问题，减轻预测误差的负面影响。

多智能体协同观测轨迹优化问题可以描述为：

即，求解J当最大时，满足速度和转向角速度约束的最优控制输入u。具体算法步骤如下：

1）已知k 时刻目标的运动状态为x，预测目标在［k+1，k+T］时间段内的运动状态为：

2）根据智能体的状态x（k）预测其在［k+1，k+T］时间段内T 步控制序列为：

3）采用基于无色信息滤波（UIF）的的集中式融合估计算法（见表1）优化控制序列，得到智能体的最优控制角度变化率序列：

表1 基于UIF 的集中式融合估计算法

4）截取控制角变化率序列的前σ（1≤σ≤T）段，在时长为σ 的时间里，用u［k+1，k+σ］来控制智能体的运动角度。

5）在k+σ 时刻，重复进行步骤1）和步骤2）。

5 仿真实验与结果分析

实验中使用2 个移动智能体跟踪目标，其角度变化率范围为［-0.1 rad/s，0.1 rad/s］；目标的运动模型有匀速直线运动和匀速率转弯运动，多智能体协同跟踪目标采用表1 的UIF 算法，设定RHO 算法中的=20，σ=1。进行下面两个仿真。

仿真实验1：目标做匀速直线运动

在实验中，两个移动智能体的初始位置为（x，y）=（-10，0），（x，y）=（5，-10）。两个智能体的速度为2 m/s，初始运动控制角度皆为π/4。

由图3（a）可知，当目标做匀速直线运动时，智能体1 和智能体2 都能持续地跟踪目标；由图3（b）可知，在跟踪过程中用于优化的目标函数J的值随时间不断增大到最大值后保持稳定，表明在已知观测值Z的条件下，对目标状态估计x的确定性越来越大；由图3（c）可知，在初始状态时滤波轨迹与真实轨迹有一定偏差，随着算法的迭代，滤波轨迹与目标的真实轨迹几乎重合；由图3（d）可以看出，系统误差随时间变化呈振荡减小的趋势，并保持在很小的范围。

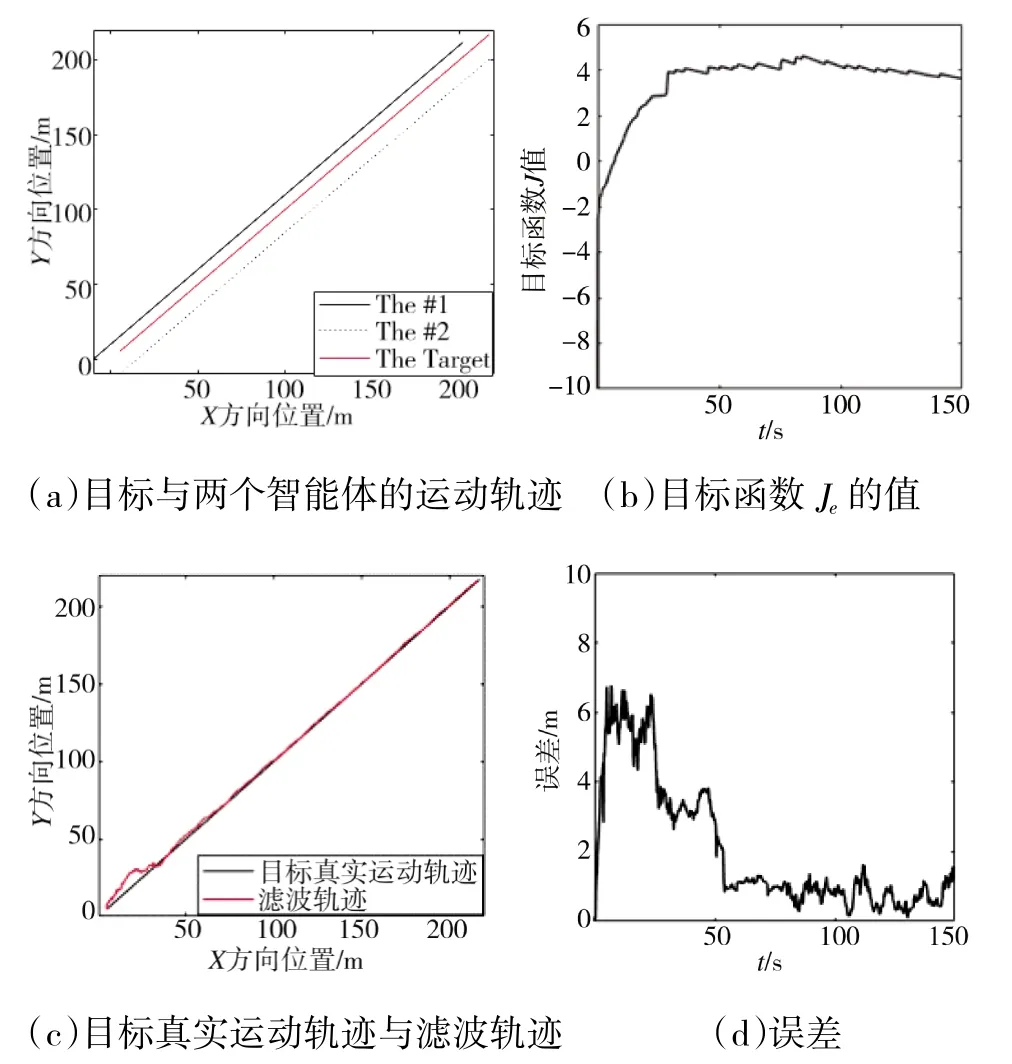
图3 目标做匀速直线运动

仿真实验2：目标做匀速率转弯运动

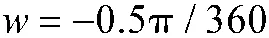
由图4（a）可知，当目标做匀速率转弯运动时，智能体1 和智能体2 能持续地跟踪目标；由图4（b）可知，优化目标函数J的值随时间不断增大，表明系统对目标状态估计x的确定性越来越大；由图4（c）可知，滤波轨迹与目标的真实轨迹有较小偏差，随着算法的迭代，滤波轨迹与目标的真实轨迹几乎重合；由图4（d）可以看出，系统误差随时间变化持续减小，误差降低到1 m 以内。

图4 目标做匀速率转弯运动

由上面两组仿真的结果可知，不论目标做匀速直线运动还是匀速率转弯运动，多智能体系统都能持续跟踪目标，且目标函数值持续增长最后保持稳定，这表明系统能够保持优化的协同观测轨迹。在仿真当中可以看到，该系统目标跟踪误差值随着算法的迭代持续下降，这说明基于信息熵的多智能体协同观测轨迹优化设计能够减少估计误差，维持对目标的观测。

6 结论

本文针对多个移动传感智能体协同跟踪单目标的问题，研究了一种基于信息熵的协同目标跟踪轨迹优化方法，改进的思路在基本RHO 算法的基础上，引入互信息作为目标状态融合估计的性能评价指标。仿真结果表明多个智能体能够持续跟踪目标获取其状态估计，跟踪误差随算法的迭代运行持续减小，证实了算法的有效性。文中面向最优目标状态的轨迹优化方法建立在集中式多平台传感器信息处理的基础上，后续将深入研究在分布式多Agent 协同观测系统中目标函数的选取问题。