爆炸冲击波信号的降噪处理*

2022-09-16熊振宇裴东兴崔春生

火力与指挥控制 2022年8期

梁晶，熊振宇，裴东兴，崔春生

（中北大学，太原 030051）

0 引言

爆炸冲击波信号具有上升沿陡峭，呈指数形式衰减，正压持续时间较长等特点，下页图1 是典型的非平稳信号。冲击波信号在频谱上分布广泛，能量主要集中于低频段，在高频段占比较低。在实际的爆炸冲击波试验中受震动冲击、强电磁场、高温等恶劣的测试环境影响，捕获的冲击波信号中通常会混入一定的环境噪声，同时传感器的敏感元件、传感元件输出的电信号，在测试系统的模拟部分会不可避免地引入干扰与高频噪声。为减小上述因素的影响，需要对实测冲击波数据进行一定的降噪处理。

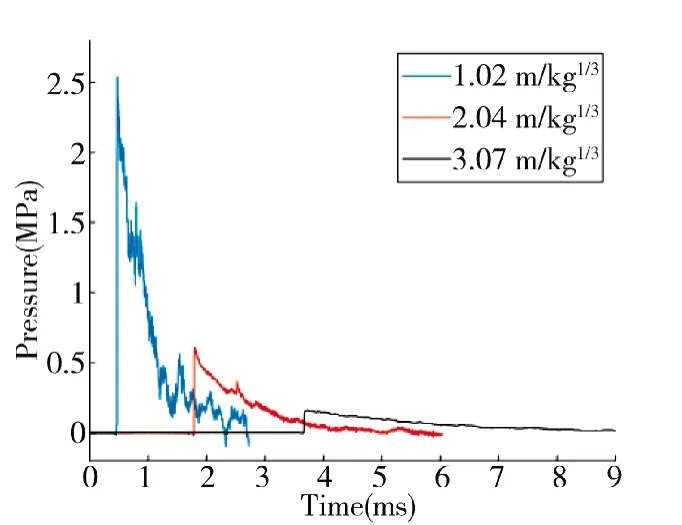
图1 实测冲击波超压信号，波形从左至右分别为比例距离在1.02 m/kg1/3，2.04 m/kg1/3，3.07 m/kg1/3 处地面测点捕获值，信号采样率为1 MHz

工程中一般采用数字低通滤波器去除信号中的噪声与干扰，文献［5-6］就以40 kHz 作为截止频率，搭建各类FIR 与IIR 数字滤波器对冲击波数据进行了处理与分析。实测的冲击波信号在时域中存在大量的尖峰与突变，这些区域含有丰富的高频信号，能够体现毁伤工况下信号的部分特点。由于高频信号与噪声的频带存在混叠，如果采用低通数字滤波器处理，会导致捕获的冲击波数据过于平滑，丢失部分有效信息，影响毁伤参数的判别与计算。

近些年随着非平稳信号处理技术的发展，小波分析、EMD、VMD-WT 等降噪方法获得了广泛关注与应用。小波阈值是一种成熟且广泛使用的降噪算法，根据信号和噪声在小波分解后的各系数中分布特性的不同，通过一定的规则对含有噪声的信号系数进行阈值量化处理，去除噪声并保留真实信号。

EMD（经验模态分解）是Huang 提出的一种用于分析非线性与非平稳信号的方法，该方法可以自适应地将信号分解到有限的固有模态函数中（IMF），通过将全部IMF 分量相加可获得原始信号。EMD 算法在分解过程存在模态混叠现象，表现为某些IMF 分量中会出现不同时间尺度的成分。针对该现象，Wu 等提出了EEMD 算法，通过添加不同的白噪声，减小EMD 算法在分解过程中由极值点跳变引起的混叠问题。但是EEMD 算法也存在：残余噪声引起重构信号畸变；初始参数的不同导致信号分解层数有所差异等不足。

EMD 及EEMD 算法分解出的IMF 分量按频率由高至低排列，因此，可通过针对若干分量进行处理并重构，实现原信号的低通滤波。传统的降噪方法通过直接去除一些高频IMF 分量实现信号的去噪，这可能会导致信号中的有效成分丢失，同时造成重构信号存在失真现象。为避免直接剔除高频IMF 分量导致的信号丢失有效成分与畸变等问题，文献［9-11］提出了一系列基于EMD 或EEMD 的联合降噪方法。由于EMD 及EEMD 算法存在的模态混叠、重构信号畸变等现象。采用基于EMD 或EEMD 的联合降噪方法，在对冲击波信号进行降噪时效果并不理想。

针对上述问题，本文提出了CEEMDAN-小波联合降噪处理方法，对爆炸冲击波信号进行降噪处理，用于提高测试数据的准确性与可靠性。

1 CEEMDAN - 小波阈值联合降噪方法

CEEMDAN-小波阈值联合降噪（简称为“联合降噪”）算法是传统EMD 降噪算法的一种改良，该方法由两部分组成。第1 部分对原始信号进行CEEMDAN 分解，第2 部分对分解后的部分IMF 分量进行小波阈值降噪处理，处理后对各分量进行重构实现原始信号的降噪。

原始信号经过CEEMDAN 分解后，得到了一组频率由高至低排列的IMF 分量，文献［13］将各IMF分量自相关函数的标准差作为指标，用于衡量该分量是否由噪声主导，本文将采用这一判别标准。

图2 CEEMDAN 分解后IMF 与剩余分量

2 信号分析与噪声模型建立

2.1 含噪冲击波压力-时间模型

冲击波超压值随时间变换的规律可采用修正的Friedlander 公式描述（式4），式中p为环境气压；ΔP 为理论超压峰值；为正压时间；α 为衰减系数。其中，衰减系数α 可通过式（5）确定，超压峰值根据GJB 6390.3-2008 采用Sadovskii 经验公式进行计算，正压作用时间参数选用姬建荣等提出的TNT 爆炸冲击波正压时间修正公式计算。

修正Friedlander 公式：

在确定等效TNT 当量、测点距离、材料系数等参数的条件下，可依据上述公式得到理论压力-时间曲线。以下本文将对实测信号进行分析，并讨论如何向理论超压曲线中添加噪声。仍然以图1 中比例距离在3.07 m/kg处测点捕获的信号为例，选用sym8 小波基对信号进行6 层小波分解与重构，重构后误差为3.641×10失真程度极低，能够满足信号分析的精度要求，重构后细节分量d4～d1 绘制在图3 中。

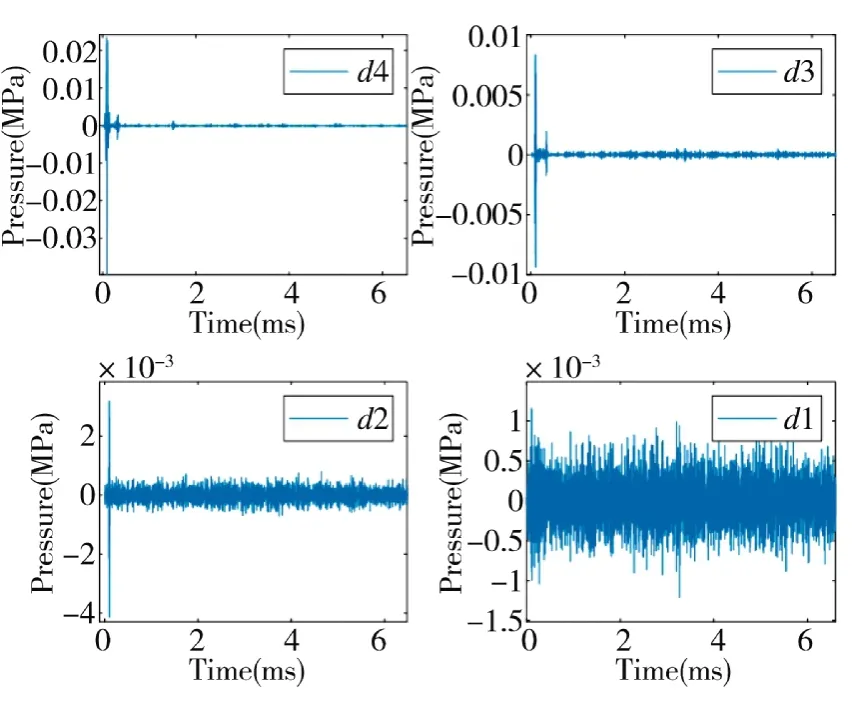
图3 信号的分层重构

图中d4～d3 为信号的62.5 kHz～125 kHz 中频部分，占有0.055%的信号能量。这两个频段的信号在0.109 ms～0.391 ms 处存在幅值较大的震荡情况，这一区域主要反映了冲击波信号中尖峰或突变信号的高频成分。d1、d2 是信号的高频部分，分别对应250 kHz～500 kHz 与125 kHz～250 kHz 频段，可以看出与其他细节分量相比，d1、d2 频段的能量在整个时域中分布比较均匀、压力值较低，可以认为这两个频段主要由噪声与干扰信号构成。

将d1 的概率密度函数绘制在图4 中，通过与多种拟合的分布曲线对比，T 分布曲线与d1 的概率密度函数重合性最大，通过构造符合该T 分布参数的序列，进行滤波处理，可获得符合d1 频段信号规律的高频噪声，同理计算d2 频段的噪声，将两构造的噪声相加便获得了3.07 m/kg处实测信号的近似高频段噪声。以此类推对1.02 m/kg，2.04 m/kg处实测信号进行同样处理。

图4 d1 概率密度函数

假定装药的几何中心距离刚性地面1.5 m；材料系数η 为1；p=0.101 3 MPa；计算比例距离在1.02 m/kg、2.04 m/kg、3.07 m/kg处的理论压力-时间曲线，根据上文对实测信号的噪声分析，对不同比例距离的理论曲线分别混入对应的高频段噪声，得到含噪的3 类信号模型，如图5 所示。从左至右将1.02 m/kg、2.04 m/kg、3.07 m/kg处含噪模型分别命名为模型A，B，C。

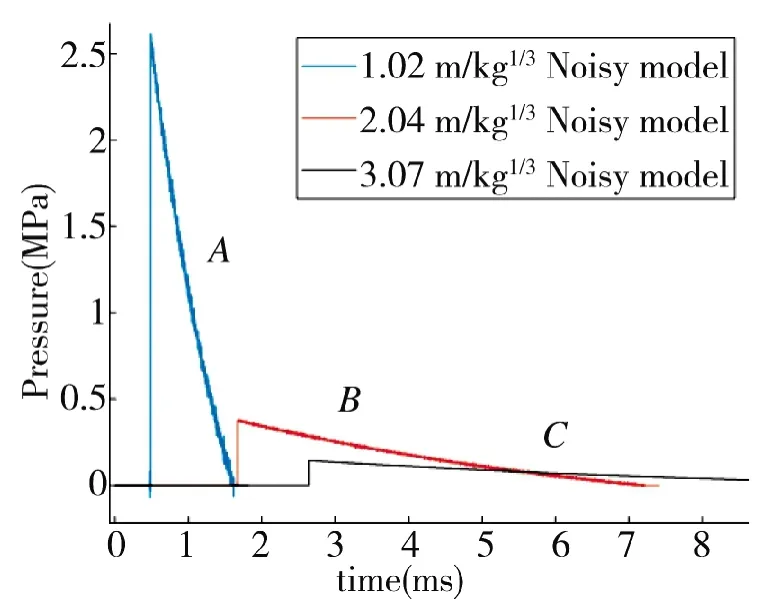
图5 含噪冲击波压力时间模型

2.2 降噪效果评价指标

本文引入了信噪比（SNR）与均方误差（MSE）来量化不同算法对含噪模型的处理效果。信噪比用于衡量信号与噪声的比值，SNR 值越大信号中噪声的含量越小。均方误差是两个序列之间距离平方和的均值，MSE 值越小两序列的偏离程度越低。

信噪比SNR 公式：

均方误差MSE 公式：

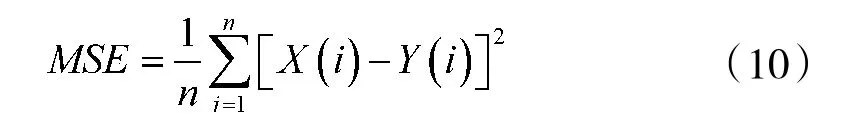
式中，X 为不含噪声的模型序列，Y 为进行对比的序列，n 是序列的长度。计算上节构建的A、B、C 3 个比例距离下模型的评价指标，并统计至表1 中。可以发现比例距离较近的A、B 模型信噪比偏低，分别为32.786 dB 与33.46 dB，同时均方误差较高，与之相比3.07 m/kg1/3 处模型的信噪比更高，均方误差偏小。这符合冲击波测试中，近场测点受测试环境影响较大，捕获信号中含有大量噪声与干扰，而远场测点相对而言受影响较小的实际情况。

表1 含噪模型的评价指标

3 实验及验证

3.1 含噪声模型的降噪实验

分别采用Bessel 低通滤波、Butterworth 低通滤波、EMD 降噪以及联合降噪（CEEMDAN- 小波阈值联合降噪）方法对上文中构建的A、B、C 含噪冲击波模型进行降噪处理，得到的降噪指标记录在表2 与表3 中。在联合降噪方法中，小波基选为sym8，分解层数为2 层，阈值估计规则为Bayes，硬阈值函数去噪。数字滤波器的阶数定为6，截止频率选择40 kHz。

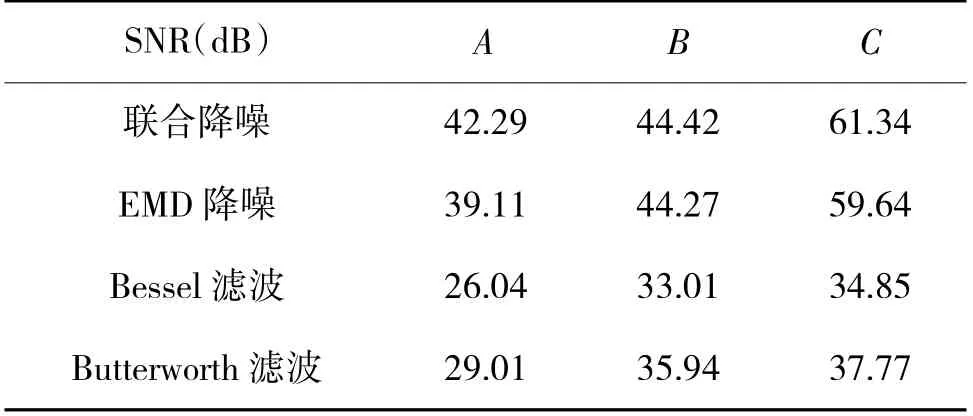
表2 降噪后模型SNR 指标

表3 降噪后模型MSE 指标

表2 中各方法处理后各模型的SNR 指标从高至低分别为联合降噪、EMD 降噪、Butterworth 低通滤波、Bessel 低通滤波。联合降噪方法处理后的信噪比提升最高，与原始含噪模型相比增加了9.51 dB、10.96 dB、10.03 dB，与EMD 降噪方法相比提升了8.13%、0.34%、2.85%。表3 中的MSE 指标也可获得相似的结论，联合降噪方法处理后MSE 指标是4 种处理方法中最低的。与原始指标相比，联合降噪方法处理后的MSE 值分别降低了88.62%、91.95%、88.74%。EMD 降噪处理后的指标与联合降噪比较接近，但仍存在9.26%的差距。

同时从上表中可以发现，模型经过Bessel、Butterworth 数字低通滤波器处理后，SNR 指标整体上呈下降趋势，MSE 出现不同程度的上升。该现象的主要原因之一是，数字滤波器在设计时各频率分量的延迟时间不同，造成滤波后信号存在一定的相位失真；另一原因则是冲击波信号模型的上升沿十分陡峭，高频分量丰富，低通滤波后信号会出现一定程度的畸变现象。

综合不同比例距离下含噪模型的降噪处理结果可以看出，Bessel、Butterworth 数字低通滤波器的降噪指标较差，这与滤波器本身特性相关。而联合降噪与EMD 降噪方法均能够降低、减小模型中的噪声含量，与EMD 降噪算法相比，联合降噪法虽然在运算时间与资源占用上有一定劣势，但该方法解决了EMD 降噪算法中存在的模态混叠与重构信号失真等问题，并且在模型降噪实验中获得了更好的处理结果。以下本文将在实测冲击波信号中验证CEEMDAN-小波阈值联合降噪方法的降噪能力。

3.2 实测信号验证

为验证CEEMDAN- 小波阈值联合降噪方法在实测信号中的表现，对图1 中所示1.02 m/kg、2.04 m/kg、3.07 m/kg处地面测点捕获的冲击波信号进行降噪处理，处理效果图绘制于图6 中。

图6 实测信号的降噪处理

从图6 中原始信号及其联合降噪处理后的图像对比来看，处理后的信号在时域中的波动明显降低，信号中的高频毛刺得到了有效抑制，该结论在3个比例距离下的实测信号处理中均有不同程度的体现。

从图6（c）超压峰值区域采用EMD 降噪、Bessel滤波、联合降噪处理后的对比结果来看，Bessel 低通滤波处理后信号出现了明显的相位失真，同时原始信号中存在的尖峰、突变等高频信息丢失，这在比例距离较近的前两个信号中表现较为明显。EMD 降噪算法对相位影响较小，但该算法受频谱混叠影响，而且直接去除高频IMF 分量，会造成真实信号中高频信息的丢失，也容易导致重构信号出现畸变。在第3 个原始信号（original-3）的EMD 降噪处理后，重构信号在0.11 ms～0.13 ms 内出现原始信号不存在的尖峰区域。

与数字滤波器和EMD 降噪算法相比，联合降噪算法几乎没有相位失真的问题，并且较好地保留了原始信号中存在的尖峰、突变等信息。从毁伤评估角度来看，原始信号的超压峰值为2.539、0.608、0.161 MPa，比冲量为1 196.37、509.44、344.05 Pa·S；联合降噪算法处理后超压峰值为2.540、0.604、0.160 MPa，比冲量：1193.39、509.23、344.03 Pa·S，处理前后对毁伤评估指标的影响较小。

综合上述结论，CEEMDAN-小波阈值联合降噪方法，能够有效地去除非平稳信号中的噪声，尽可能地保留了信号中的高频成分信息。对于爆炸冲击波信号而言是比较理想的降噪方法。