关于泡利矩阵的几点讨论
2022-09-16黄兴奎
黄兴奎
(荆楚理工学院 数理学院,湖北 荆门 448000)
0 引言
泡利矩阵是量子力学中的重要矩阵,目前所见文献主要讨论它的各种导出方法、在不同表象中的表示、解析量子力学中的典型计算问题等等。实际上,泡利矩阵是在讨论电子自旋时引入的,不仅对于研究自旋问题、处理相对论性的狄拉克方程时非常方便,而且在量子信息、量子光学等新兴学科中也有重要应用,可以从逻辑上实现量子非门X、量子位相门P(θ)、Hadamard门H,利用合适的脉冲就能从物理上实现上述量子门,从而为量子计算奠定必要的基础。因此,讨论泡利矩阵的性质,在量子力学理论中的基础作用,以及在量子信息中的应用,有助于加深对于泡利矩阵的理解。
1 泡利矩阵的基本形式


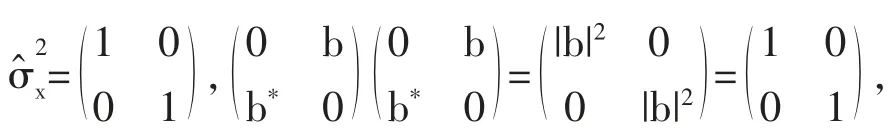
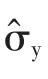
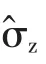


2 泡利矩阵的基本性质
为了后面讨论问题的方便,简单介绍一下泡利矩阵的基本性质。
(1)不对易性
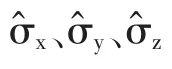

(2)反对易性
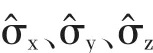
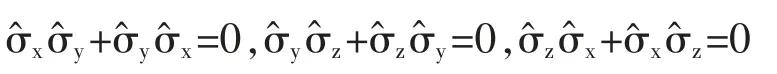
(3)自逆性
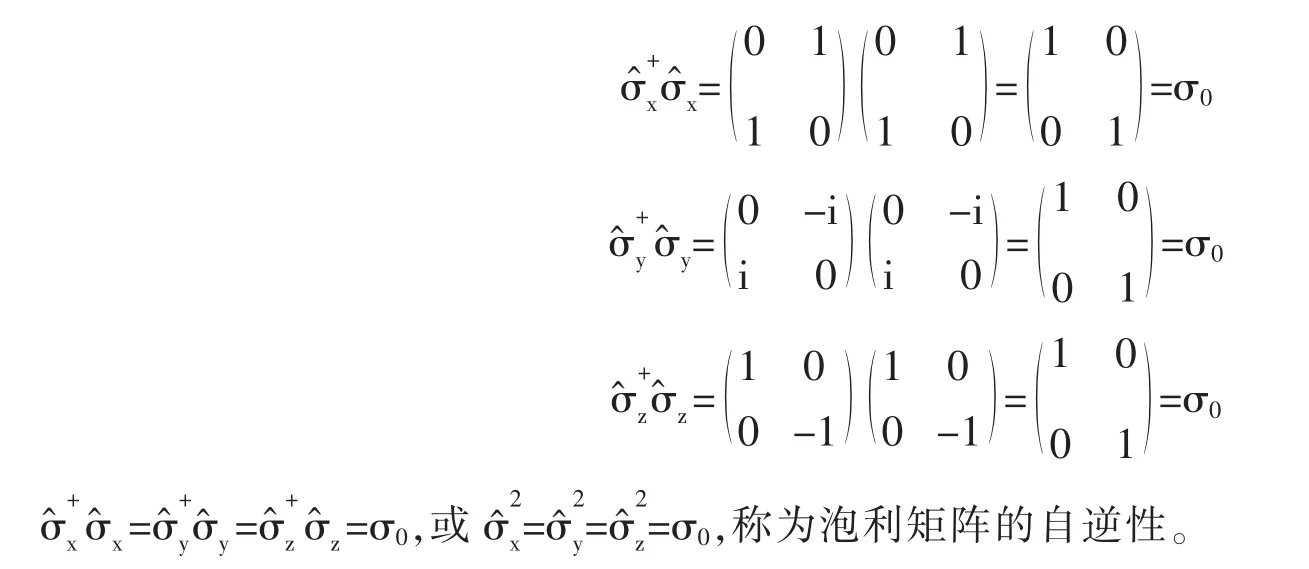
(4)零迹性
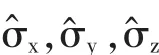
3 泡利矩阵在量子力学理论中的应用
3.1 展开任意厄米算符
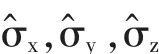
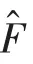
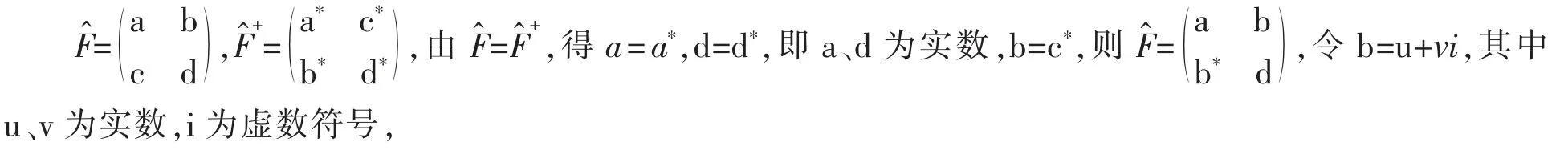
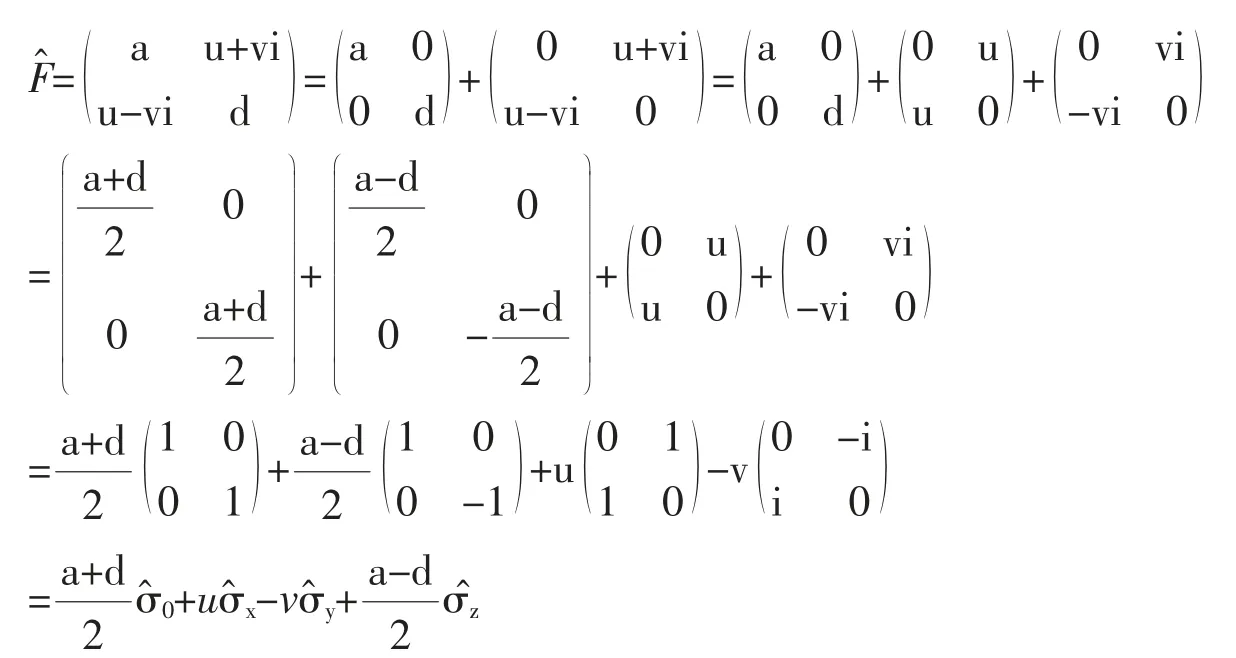

3.2 研究电子或其它粒子的自旋问题
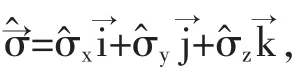

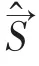
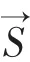

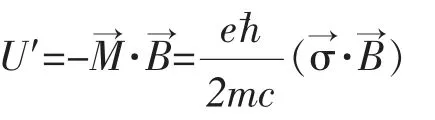
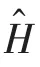
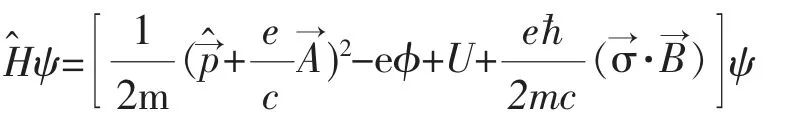

3.3 处理相对论性的狄拉克方程
薛定谔方程只适用于低能或非相对论的情况。研究高速运动的高能粒子,必须同时考虑狭义相对论和洛伦兹不变性。由于薛定谔方程对时间和空间的导数分别是一阶和二阶的,因此不是洛伦兹不变的。自旋是电子内禀的属性,在非相对论情形下,泡利方程将自旋作为一种新的自由度添加到薛定谔方程上处理。在相对论情形下,狄拉克方程将自旋这个内禀自由度很自然地体现在该方程的旋量结构上,不仅如此,自旋与轨道耦合,自旋与自旋的耦合都可以包含在方程之中,而这一切,都离不开泡利算符的正确应用。
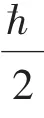
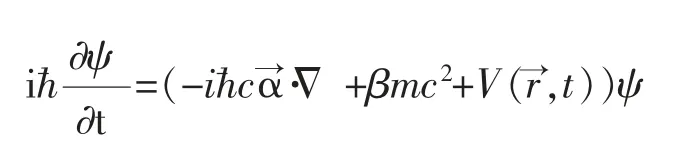
对定态问题,
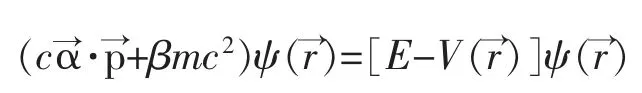

4 泡利矩阵在量子计算中的应用
量子逻辑门将输入量子态变换成输出量子态,单量子比特逻辑门是实现量子逻辑操作的基础。常见的单量子比特门有量子非门X、量子位相门P(θ)、Hadamard门H。下面讨论如何利用泡利矩阵实现这几个门的逻辑功能,并简单介绍其物理实现方法。
4.1 量子非门X
量子非门X的功能:将原子状态由上能态|1〉变换成下能态|0〉或由下能态|0〉变换成上能态|1〉,即X|1〉=|0〉,X|0〉=|1〉,由于
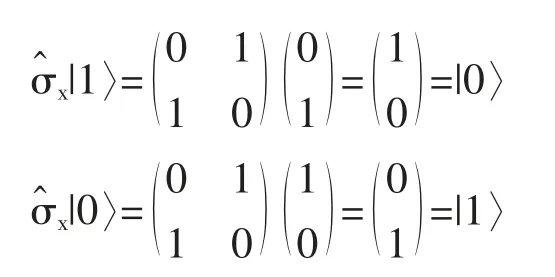
4.2 量子位相门P(θ)
量子位相门P(θ)的功能:P(θ)|0〉=|0〉,P(θ)|1〉=e|1〉。

4.3 Hadamard门H
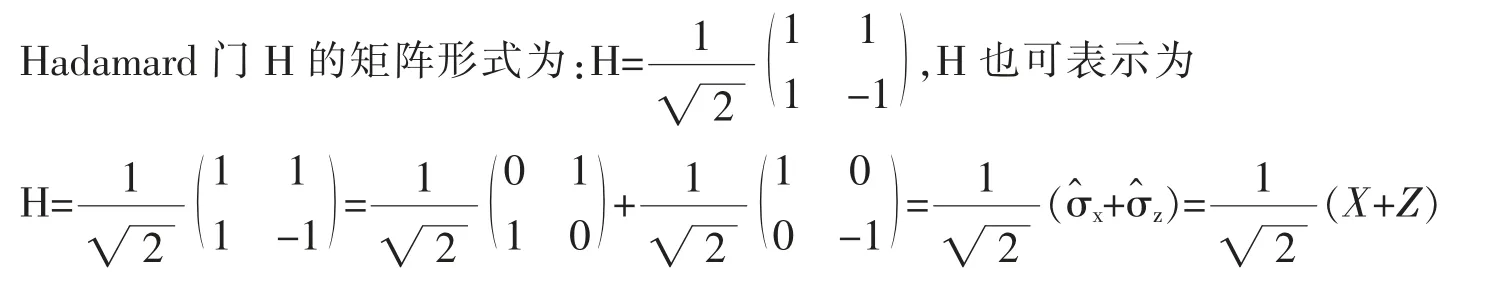
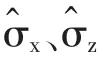
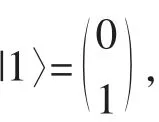
初始时处于上能态|ψ(0)〉=|1〉,则t时刻原子的量子态为:

为讨论方便取φ=0,则

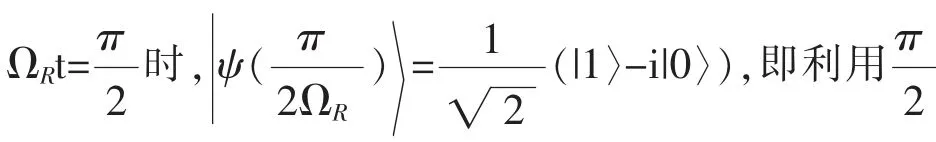
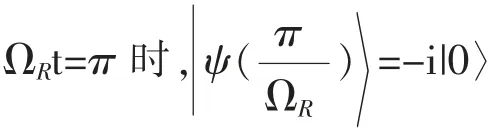
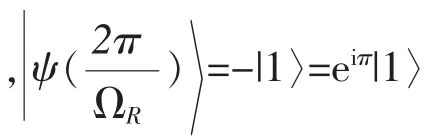
类似地,可以讨论原子初始处于下能态|ψ(0)〉=|0〉的情况,这些结果在量子逻辑门的实现中均有重要的应用。
5 结论