基于神经网络对房价预测的研究分析

郑伟鹏 司亚超

(河北建筑工程学院，河北 张家口 075000)

0 引 言

住房满足是使人民获得幸福感的重要因素.近些年来随着人民对住房需求的增高，我国的住房建筑面积也出现递增趋势，由于房价受到了诸多因素的影响，人们在买房时候很难考虑到影响房屋价格的主要因素，如果有一个模型能准确的根据影响房价的因素去预测房价趋势，将会高效的帮助人们找到房价规律[4-5].

20世纪40年代首次提出了“M-P神经网络模型”.在此之后提出MLP(多层感知机)模型和BP(Backward propagation)神经网络模型.其中BP神经网络的出现有效解决了多层神经网络隐藏层中权重学习问题.本文中我们将根据影响房屋价格的因素并结合BP神经网络的模型来实现对房屋价格的预测[1].

1 数据处理

1.1 数据集介绍

实现人工神经网络(神经网络)模型对房价的预测需要大量的数据训练模型.由于我国房价数据难以收集以及一些不可量化因素的存在所以本文中将使用1990年美国人口普查下的加利福尼亚州的房屋价格等数据进行预测，该数据集一共包含20000多个样本，其中部分数据样本如表一所示.该样本数据中包含8个特征：人均收入、房屋年龄、房间数、卧室数、房区人口数、房屋居住人数、房屋经度、房屋纬度.房价中位数是神经网络模型所要预测的结果，其余的8个变量均为特征变量，是影响房价中位数的重要因素.如图1样本数据热力图所示房间数这个特征与房屋价格的相关性系数达到了0.846两者之间具有较强的相关性，也就是说房间数量是影响当前房屋价格的重要因素.

表1 影响房价特征的数据样本

图1 样本特征的热力图

1.2 数据处理

在对数据进行训练之前，需要对数据进行一些处理操作.通过求得数据集的均值、方差、最大值、最小值等来找到当前部分的整体指标，然后再通过归一化处理(如表2所示)将数据放缩到(-1，1)的区间上.

表2 归一化处理后的数据样本

使用归一化处理数据的好处主要有两点：一是可以加快模型的收敛速度，较大的数据在训练过程中可能出现梯度爆炸，数据通过归一化处理可以防止在梯度下降过程中模型的迭代速度较慢.二是可以提高模型的准确度由于这八个变量中的具有不同的数量级，如表1所示的5个样本中房区人口数的平均值为868，而平均卧室量的平均值为1.样本数据中不同特征之间数量级相差太大，可能会导致训练过程中数值较高的特征对网络权重的影响比较大，削弱了数值小的特征对结果的影响.为了保证神经网络在训练时对样本不同特征之间的“公平性”所以需要对样本数据进行归一化处理.

2 神经网络模型

2.1 神经网络模型

神经网络通常定义为三部分:输入层、隐藏层、输出层.其中输入数据作为第一层，神经网络预测的结果作为最后一层，输入层和输出层之间的统称为隐藏层.这三层的结合模拟了生物学神经网络结构，神经网络模型如图2所示.

2.2 前向传播

神经网络的前向传播可以简单的理解为矩阵相乘.神经网络节点模型如图3所示，W1、W2、W3作为神经网络的输入，这些输入与该分支的权重x1、x2、x3分别相乘然后累加得到输出y.因为y是输入值与权重值相乘得到的线性值，所以需要再通过非线性函数S用来模拟神经元传递信号的阈值处理.最终得到的值A就是经过这个神经网络节点的结果.

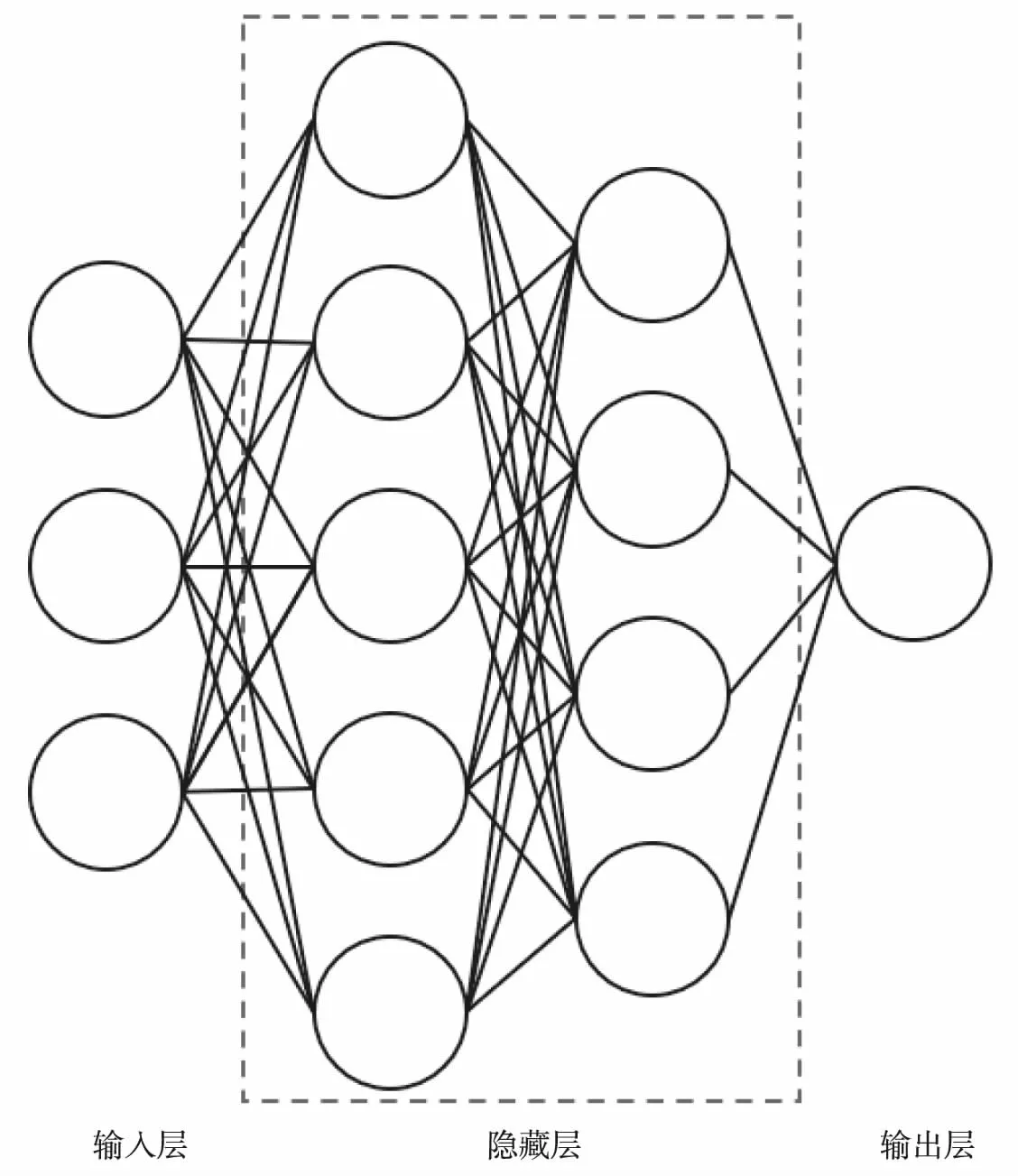
图2 神经网络模型

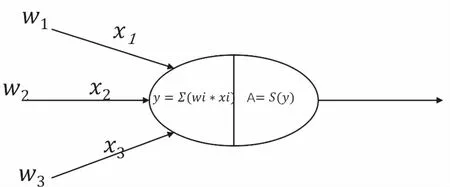
图3 神经网络结节点图

2.3 反向传播

样本数据在经过神经网络运算后会输出相应的预测值，为了提高神经网络的准确度需要更新神经网络的权重，通常需要将预期值和神经网络模型输出值代入到损失函数中进行计算，然后根据链式求导法则，由输出层向输入层去更新神经网络各层之间节点的权重，使得权重和输入的数据计算出的结果能够接近预测的数值，从求误差到更新权重的过程我们就称为神经网络的反向传播.神经网络预测模型重常用的损失函数是交叉熵损失函数(公式1)和均方差损失函数(公式2).

(1)

(2)

3 实 验

在本次实验中输入层的格式统一是[32,8](一次处理32个样本数据，每个样本数据有8个特征)，输入层的第一个参数是根据电脑性能决定的，神经网络一次处理样本数据的数量，在电脑性能得到保证的情况下该值越大就会使得神经网络模型训练的速度越快，这个参数并不会影响神经网络模型的精准度.第二参数是训练的样本的特征决定的，本文选取数据集的特征是8所以该值就是数据特征数量，因为计算机是二进制所以隐藏层节点的设置为2的倍数.

神经网络模型隐藏层的选取则在2、3层.如果神经网络模型的层数太少则可能导致神经网络的参数太少无法很好的拟合样本数据中的特征得到准确的预测值，如果隐藏层数太多则可能导致网络模型的性能下降.为了提高网络模型的鲁棒性，本文中的所有实验在第二个隐藏层添加了Dropout随机失活函数，随机将部分隐含层节点的权重归零，由于每次迭代受影响的节点不同，因此各节点的“重要性”会被平衡这样会使得神经网络模型更加的健壮.

在神经网络模型优化中本实验选择了SGD(Stochastic Gradient Descent)优化器，相比其他优化器SGD优化器在计算中不易于陷入局部极值点.损失函数则选用了均方差损失函数，因为均方差相比于交叉熵损失函数更加适合回归问题.

实验参数如图表3所示，当神经网络的隐藏层数为2且每个节点的个数为64时神经网络模型取得66.97%的准确度，此时对应测试集的预测图如图3所示.

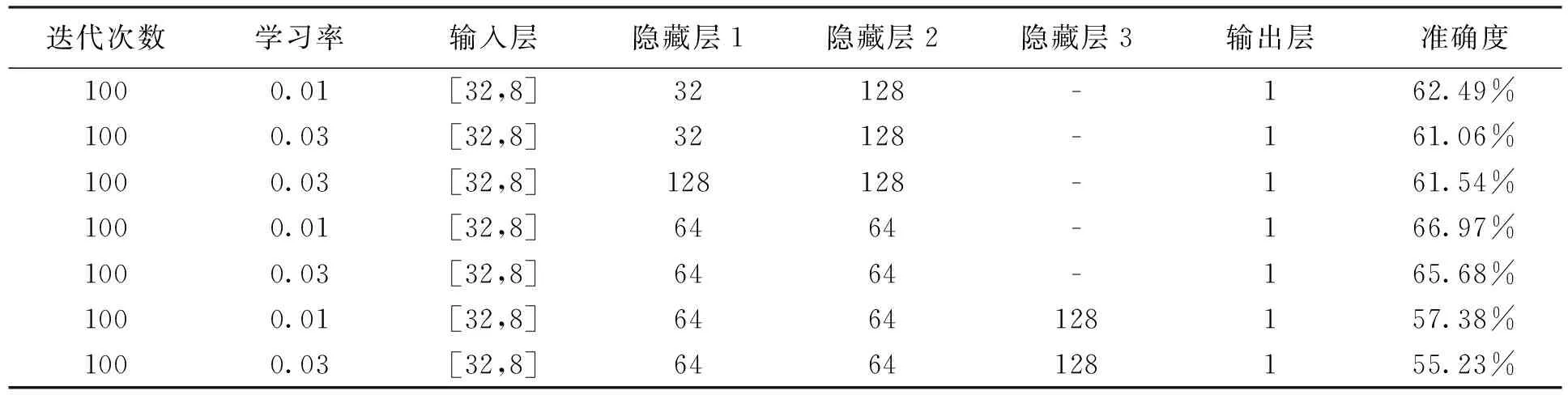
表3 实验参数

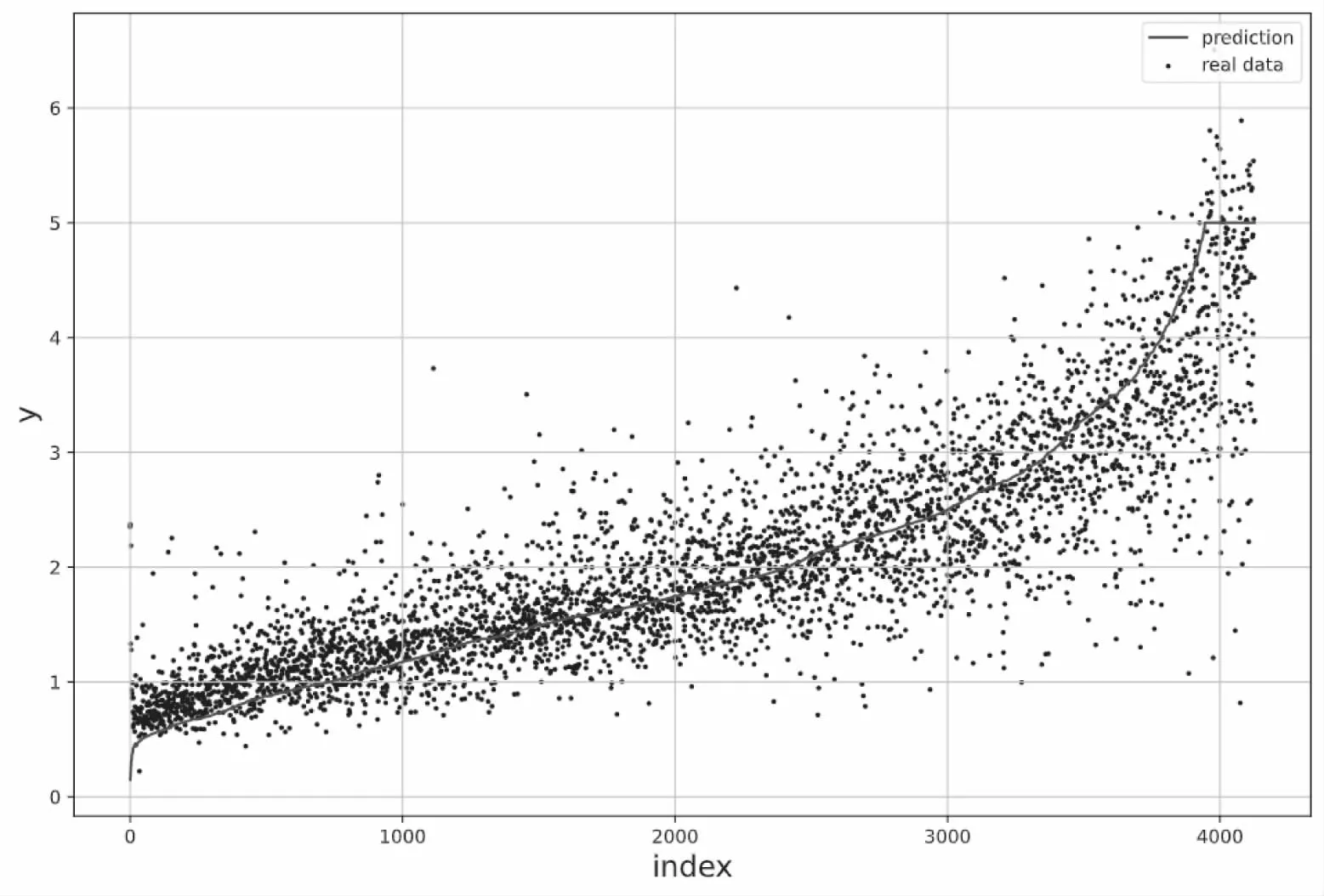
图4 神经网络预测曲线

4 结束语

本文通过加利福尼亚州的房屋价格数据作为实验数据证实了神经网络对房价预测的良好表现，针对于大规模多特征的房价数据神经网络有着较好的拟合能力.在未来的研究中，如果可以量化影响我国房价的因素，神经网络模型对于我国的房价的预测将会达到一个不错的效果.