高速铁路板式轨道和大地的振动预测及对连续轨道板模型的讨论
2022-09-15彭宇豪圣小珍张皓迪岳松涛
彭宇豪,圣小珍,张皓迪,岳松涛
(1.上海工程技术大学 城市轨道交通学院, 上海 201620;2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
随着铁路附近建筑用地的增加以及公众对振动和噪声问题认识的提高,铁路引起的环境振动问题受到人们的广泛关注,成为影响高速铁路和城市铁路网可持续发展的重要问题之一。因此开展对环境振动的研究十分必要,其中一个重要方面,就是铁路环境振动的预测。
已有许多研究者建立铁路环境振动预测模型。预测模型包括经验模型、数值模型和解析模型。对轨道结构和大地做一些简化,可以建立具有高计算效率的解析(或半解析)模型,通过这些解析模型的分析计算,揭示铁路环境振动的特性。Dieterman[1]认为当列车速度接近弹性半空间的临界速度时,会激发大地的特征波,使大地的振动水平显著上升。文献[2-4]基于传递矩阵法建立了固定和移动荷载作用下环境振动的解析模型,系统响应在频率-波数域中求解。轨道被简化成沿着纵向(轨道延伸方向)不变的结构,土壤为水平分层结构且服从线弹性假设。和振兴[5]使用文献[2-3]的方法,将轨道板假设成无限长的梁,研究了板式轨道交通引起的环境振动问题。
现有的解析模型通常将轨道系统简化成沿着纵向不变的结构,即2.5D结构。但实际上钢轨的周期离散支承、轨道板的分段浇筑或预制轨道板的铺设,都使得轨道结构是一个周期结构。Hussein等[6]基于周期结构理论考虑轨道板的离散分布,但分析仅针对于地下轨道交通。对铺设在大地表面的高速铁路,考虑轨道/大地结构周期特性的地面板式轨道交通环境振动预测模型还有待建立。同时,已有的预测模型将不连续的轨道板简化为连续无限长的欧拉-伯努利梁,此简化对大地振动的影响并未得到充分的研究。本文将轨道/大地系统作为一个无限长的周期结构,建立地面的板式轨道交通诱发的环境振动预测模型,同时考虑钢轨的离散支承和轨道板的离散分布。通过傅里叶变换、周期结构理论和频率-波数域中大地的动柔度求解系统的响应,其中边界自由的轨道板的振动使用模态叠加法表示,模态叠加系数在频率-空间域中求解。通过将预测结果与已有模型预测结果进行对比,明确了轨道板简化对环境振动预测的影响。
1 轨道/大地系统运动微分方程及对移动简化荷载响应的求解
已有研究表明,在轨道板下使用低刚度的减振垫,可以减少振动向轨下系统的传递,控制高速列车运行引起的环境振动问题[7-8]。本节针对这样的减振型板式轨道建立运动微分方程并进行求解。轨道/大地系统见图1,包括钢轨、轨道板和混凝土底座。钢轨由离散的弹簧(扣件系统)支承,轨道板下的减振层表示为连续分布的弹簧。钢轨和混凝土底座分别简化为无限长的铁木辛柯梁和欧拉-伯努利梁,而边界自由的轨道板则表示为有限长的欧拉-伯努利梁。通常认为,钢轨在高频激励下会发生剪切变形,铁木辛柯梁比欧拉-伯努利梁更适合于确定钢轨在高频下的动力响应,但在低频下它们是等效的。对自由的标准60钢轨的研究表明,欧拉-伯努利梁理论可以适用于大约300 Hz以下的振动。然而,文献[9]表明,由于钢轨不是自由钢轨,而是受到来自扣件的横向力的作用,这些横向力所产生的剪切变形使得欧拉-伯努利梁理论即使是在频率很低时也会产生较大的误差。本文认为将钢轨简化为铁木辛柯梁比欧拉-伯努利梁更为合适。如图1所示,轨道/大地系统在纵向是一个无限长的周期结构,周期为L。假定每个轨道板上有K个扣件,扣件间距为l。第j个子周期位于[jL,(j+1)L],包含了第j个轨道板,其中j=-∞,…,0,…,+∞。x轴的原点位于第0个子周期轨道板的左端。

图1 轨道/大地系统示意图
当移动速度为c,频率为Ω的简谐激励P0eiΩt作用在钢轨上,钢轨的振动可表示为
(1)
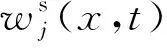
将式(1)对x和t作傅里叶变换,得
(2)
式中:对x的傅里叶变换记为“-”,对应波数β;对t的傅里叶变换标记为“^”,对应频率f。
根据周期结构理论可得[10-12]
(3)
式中:
β*=(Ω-2πf)/c
(4)
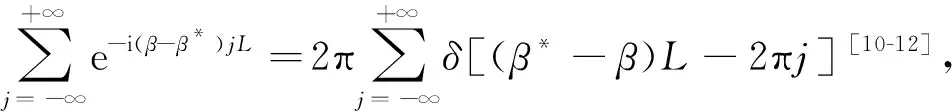
(5)
令
根据在转动方向上钢轨垫片的动刚度kψ=bs2kP/12(bs为垫片长度),并由式(5)可得频率-波数域中钢轨的位移为
(6)
将式(6)对波数β作傅里叶逆变换得到钢轨的位移频谱
式中:
βj=β*-2πj/L
(8)
第0个子周期内轨道板的振动位移可以通过模态叠加法表达为
(9)
其中,
φs(ξ)=cosh(λsξ)+cos(λsξ)-
Fs[sinh(λsξ)+sin(λsξ)]
Fs=[sinh(λsL)+sin(λsL)]/
[cosh(λsL)-cos(λsL)]s≥3
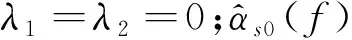
仅考虑轨道板的前S阶模态,对应的第S阶固有频率需满足远大于大地振动关注的频率范围(人体可感知的振动为1~80 Hz,大地振动导致的二次结构噪声为20~250 Hz)。
将式(9)代入式(7)可得
(10)
式中:
(11)
as(x,f)=
(12)
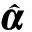
矩阵是未知的,由第0个子周期内钢轨在扣件位置处的位移频谱组成,将在式(13)~式(34)中求解。
(13)
式中:

(14)

(15)

(16)
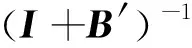
(17)
式(17)为钢轨的位移频谱,下面将用类似的方法求解混凝土底座的频谱。首先定义矩形窗函数为
(18)
则在x∈(-∞,+∞),混凝土底座的振动微分方程可表示为
(19)
式中:EBIB为混凝土底座的弯曲刚度;mB为单位长度混凝土底座的质量;k1为单位长度减振层的刚度;Fg(x,t)为大地对混凝土底座的作用力。
将式(19)对x和t作傅里叶变换并由式(2)得
(20)
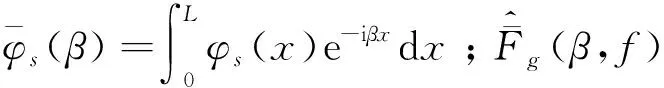
(21)
式中:γ为y方向上的波数。
在y= 0处,大地表面和轨道混凝土底座的位移存在连续性
(22)
将式(22)代入式(20)得
(23)
式中:
(24)
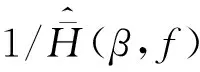
将式(23)对波数β作傅里叶逆变换可得到混凝土底座的位移频谱
(25)
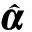
对第0个子周期内的轨道板(即j=0),其振动微分方程为
(26)
式中:ESIS为轨道板的弯曲刚度;mS为单位长度轨道板的质量。
将式(26)对t作傅里叶变换并代入式(25)(混凝土底座的位移频谱)得
0≤x≤L
(27)
将式(27)两边同乘第m阶振型函数φm(x),并利用振型函数的正交性可得
(28)
式中:
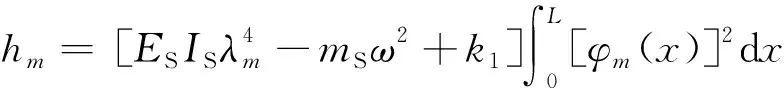
(29)
(30)
将式(28)中的m由1取到S可得以下的线性代数方程组
(31)
令
C2qR
(32)
式(31)可简写为
(33)
根据式(13)和式(33),可以得到轨道板的模态叠加系数
(34)
将式(34)代入式(17),即可得到钢轨的位移频谱

(35)
式中:
根据式(11)~式(12)、式(14)~式(16),式(35)可进一步表达为
(36)
其中,
将式(36)对频率f作傅里叶逆变换可得时间-空间域中大地的稳态响应,且根据式(4),2πf=Ω-βc=ω,2πdf=-cdβ,大地的响应最终可表示为(β*用β替代)
(37)
在随荷载移动的坐标系中,将x方向的坐标定义为x′=x-x0-ct。因此,式(37)变为
(38)
式中:x′=x-x0-ct为移动坐标系中x方向的坐标,表示响应点相对于移动荷载的位置[10-12];方括号中的项在表示移动坐标系中,频率为Ω的单位移动简谐激励下钢轨的位移导纳,它是一个关于时间t的周期函数,周期为L/c(即荷载通过一个子周期所需的时间)。
联立式(20)~式(23)、式(34),并对波数β和γ作傅里叶逆变换,得到大地表面的位移频谱为
(39)
式中:
(40)
由于多普勒效应,即使荷载以单个简谐频率振动,钢轨和大地的频谱都包含了一个范围的频率成分。对于已有的模型(将轨道/大地系统简化为2.5D结构),轨道和大地的频谱幅值关于x是独立的[2-3],而本文将轨道/大地系统作为一个周期结构,钢轨和大地的位移频谱幅值则与位置坐标x相关。
2 算例及分析
2.1 轨道结构和大地参数
本节基于上述推导研究周期的轨道/大地结构的临界速度、大地频谱以及钢轨导纳,并将结果与轨道板假设成连续无限长梁时的结果对比,明确了轨道板简化对系统响应的影响。采用的轨道参数见表1,其中减振层刚度参考文献[14],为k1=4×107N/m。

表1 轨道系统参数
大地参数见表2。由于仅考虑较低的频率范围(0~250 Hz),经过验算,关于j的无穷级数可以只考虑对j=-10,…,0,…,10的各项。对边界自由的轨道板,考虑前18阶模态,即S=18,对应固有频率为2 171 Hz,远高于大地振动所分析的频率范围,能够保证计算精度。
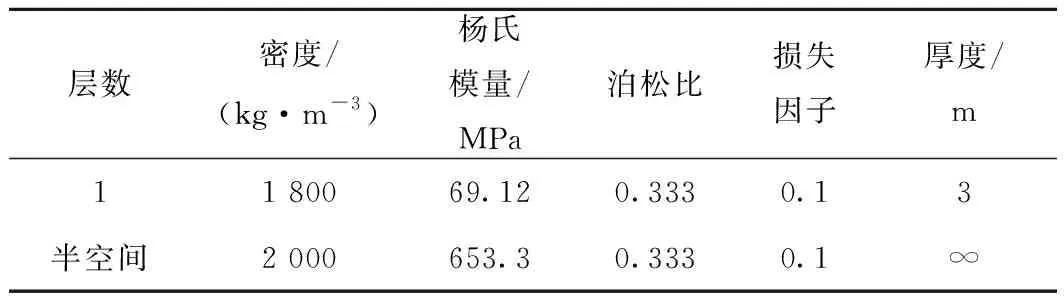
表2 大地参数
2.2 轴荷载临界速度
不同速度的单位轴荷载作用下,刚性地基上周期的轨道系统中钢轨最大位移-荷载速度曲线(上)及其频散曲线(下,亮黄曲线),见图2。对于考虑轨道板离散的周期轨道结构,存在多个峰值速度,而且随着荷载速度的降低,峰值大小明显降低同时曲线逐渐趋于平滑。图2(b)中的频散曲线存在曲线聚散(即两条频散曲线靠近又分开)现象,图2(a)中峰值速度对应的荷载-速度线(在频散图上满足“频率=波数×荷载速度/(2π)”的直线)总是穿过频散曲线的聚散点(233 m/s),或者与频散曲线相切(111 m/s和71 m/s)。频散曲线聚散现象在其他领域被广泛地研究,它和系统一种类似共振的行为有关[15]。而在荷载-速度线与频散曲线的切点(f0,k0)处,相速度为cp=2πf0/k0,群速度为cg=2π∂f/∂k∣(f0,k0),且在切点处移动荷载的速度c=cp=cg,此时相速度与群速度重叠,这通常是2.5D轨道/大地结构临界速度的产生机制[16]。图3为移动坐标系下大地最大位移-荷载速度曲线,其中周期的轨道/大地结构对应的曲线也出现了多个峰值速度。236 m/s处的峰值与图2(a)中233 m/s的峰值相对应,主要是周期的轨道系统引起的。180 m/s左右的峰值是主要由大地导致的,但被轨道系统影响。将轨道板假设为连续无限长的结构在一定程度上加强了轨道/大地系统,故预测出的临界速度(182 m/s)略高于轨道板离散时的结果(177 m/s)。周期的轨道/大地模型预测出了多个峰值速度,这与轨道板连续模型的结果存在明显的差别。

图2 刚性地基上周期轨道的钢轨最大位移-荷载速度及频散关系
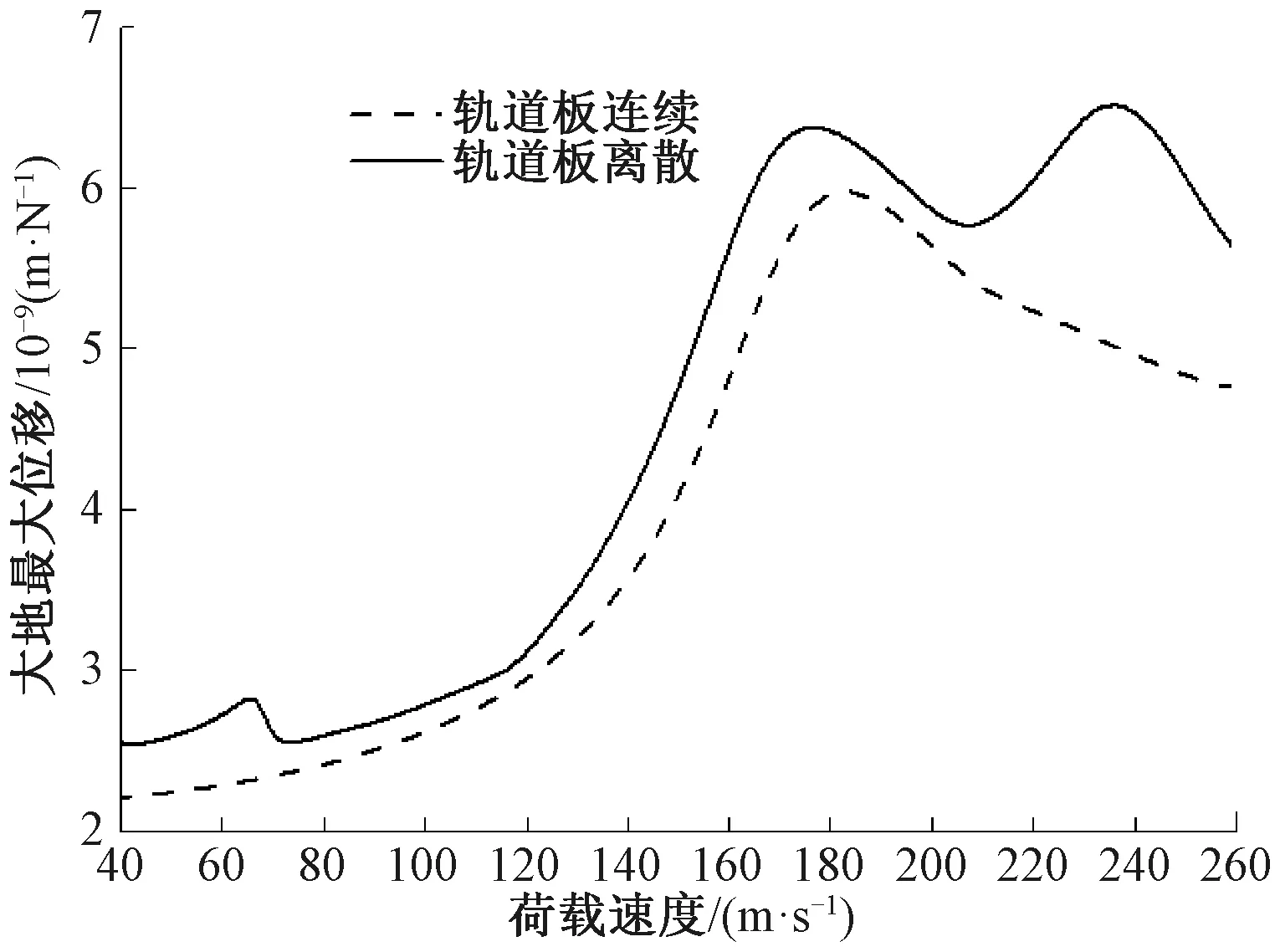
图3 大地表面最大位移-荷载速度曲线
2.3 移动简谐荷载产生的振动谱
为分析离散轨道板对系统响应的影响,首先对刚性地基上的轨道板作模态分析,减振层用等效的弹簧表示。轨道板的前5阶模态振型(彩色云图)及其固有频率见图4,前两阶模态为刚体模态,轨道板在减振层上作刚性的平动和转动,其余的模态为轨道板的弯曲模态。图4中轨道板振型对应的固有频率皆位于大地振动所关注的频率范围之内。

图4 轨道板模态及其固有频率
在荷载速度100 m/s激励频率60 Hz的单位简谐激励下,大地的频谱见图5。轨道板离散时大地频谱曲线在31.7 Hz出现了额外的峰值,图4中轨道板在33.4 Hz处也存在一弯曲模态。因此大地频谱在31.7 Hz的峰值主要是减振层上自由轨道板的弯曲模态导致的。轨道板弯曲模态对钢轨的响应也有明显的影响,将在2.4节详细地分析。当轨道板被假设成无限长时,轨道/大地系统为波导结构,在频谱曲线上有两个尖锐的峰值,这是多普勒效应的典型特征。而实际上轨道板为离散结构,即轨道/大地系统是周期结构,具有不同的波导特性(存在通带和阻带),故两条频谱曲线存在明显的差别。

图5 大地频谱
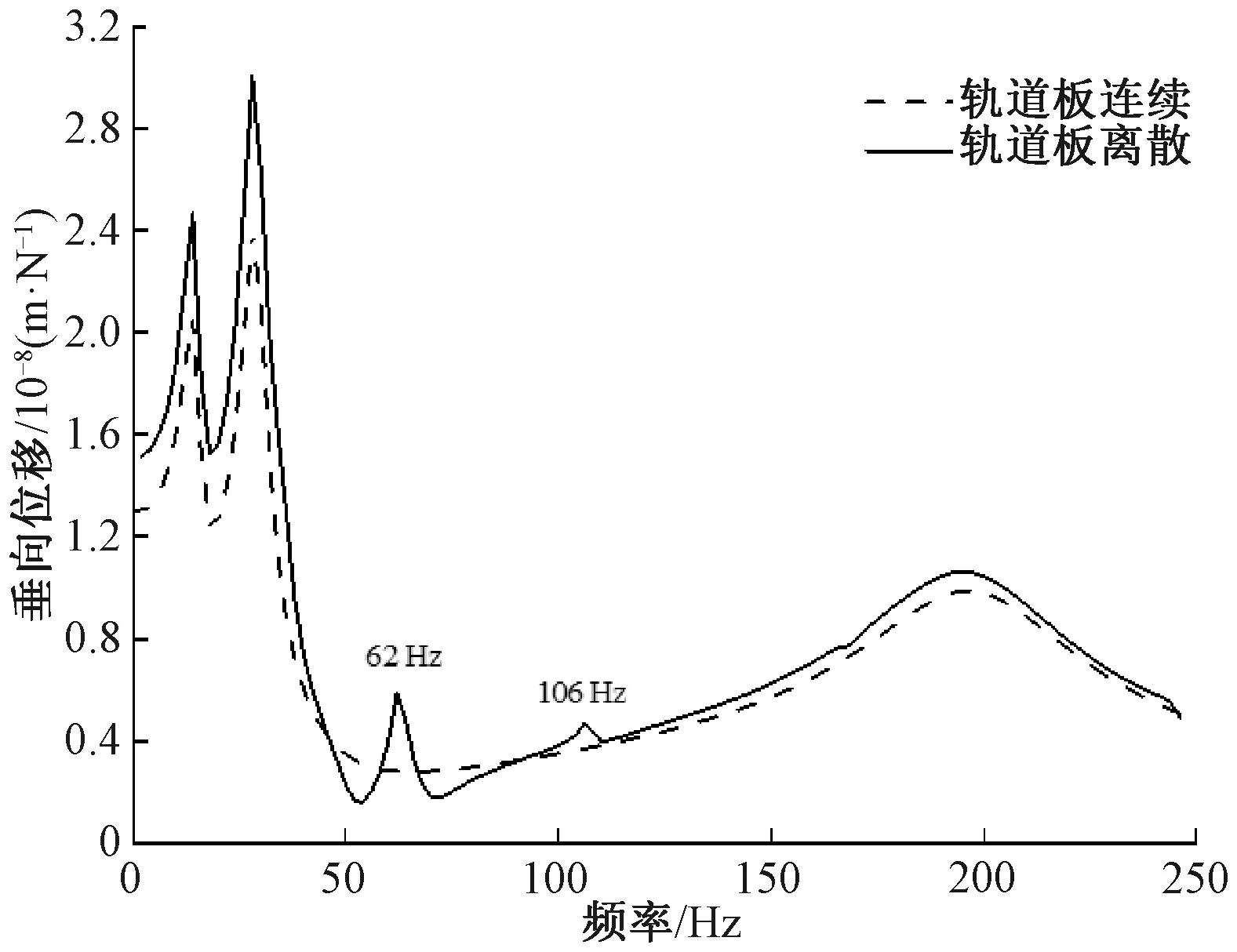
图6 钢轨导纳
2.4 轨道结构和大地的频响特性
移动坐标系下的钢轨导纳见图6,其中x′=x0=0,c=0,t=0。图6中在频率为28、195 Hz的峰值处钢轨振动类似于一个二自由度系统,峰值频率与二自由度系统的固有频率相吻合。在14 Hz处的峰值主要由层状大地的固有振动引起的,但同时被轨道系统所影响。与轨道板离散的情况相比,将轨道板假设为无限长时提高了轨道板的弯曲刚度,所以在14、28 Hz处轨道板离散时钢轨导纳具有更高的峰值。当频率提高到195 Hz时,钢轨主要在钢轨垫片上振动,轨道板是连续或离散对钢轨导纳的影响不大。轨道板离散时,钢轨导纳在62、102 Hz有额外的峰值,图4中轨道板在56.9、100.2 Hz也存在相应的弯曲模态,所以钢轨导纳在62、102 Hz的峰值仍与轨道板的弯曲模态有关。轨道板被假设成无限长时对钢轨导纳的影响会影响轮轨力的计算,进而影响大地响应的预测。
3 结论
本文基于傅里叶变换、周期结构理论和频率-波数域中大地的动柔度建立了更接近实际结构的地面板式轨道交通诱发的环境振动预测模型,即考虑了钢轨的离散支承和轨道板的离散分布,对比了本文模型与简化模型的对大地振动预测的差别。已有的模型通常将轨道/大地系统简化为纵向均匀的2.5D结构,而本文将其视为无限长的周期结构,以一减振型无砟轨道为例,通过将本文模型与简化模型的预测结果作对比,明确了将不连续轨道板假设成连续无限长的欧拉-伯努利梁对临界速度、大地频谱和钢轨导纳预测存在以下影响:
(1)对于临界速度,简化模型仅预测出了一个临界速度,其产生机制为相速度与群速度的重叠,周期的轨道/大地结构存在多个峰值速度(临界速度),其产生机制除了是相速度与群速度的重叠,还与频散曲线的聚散现象有关。
(2)对于大地频谱,简化模型中轨道/大地结构是一个波导结构,本文将其作为更符合实际的周期结构,具有不同的波导特性(存在通带和阻带),因此两种模型预测的大地频谱也会不同。离散轨道板的弯曲模态会导致大地的频谱响应出现相应的峰值,如大地频谱在31.7 Hz的峰值对应轨道板在33.4 Hz处的弯曲模态。
(3)对于钢轨导纳,与简化模型相比,本文模型中边界自由的轨道板的弯曲模态会也使钢轨导纳曲线出现相应峰值,如钢轨导纳在62、106 Hz处的峰值,对应轨道板在56.9、100.2 Hz的弯曲模态。
