用于频域参数识别选线方法的频点提取模型研究

郭平，唐兴强，李凯恩，石定中，罗玉珠，张磊

（云南电网有限责任公司临沧供电局，云南 临沧 677000）

0 前言

常见的配电网的结构往往是中性点直接接地，这就会导致在出现单向接地问题之后，接地点与中性点之间产生短路问题，从而在接地点出现较大的电流，最终导致设备出现故障或者损毁设备，这就使得供电系统的安全性下降，在对配电网设计的过程中应尽量减少这种问题，对应用中性点接地技术的应用当中应主要安全问题，尽力将此技术作为维护电网经济与安全保障的重要屏障[1]。

我国拥有较为复杂的配电网结构设计，往往在电流接地系统出现问题之后，只能产生非常微小的信号故障，所以在我国检测配电网故障就成了一个难以解决的问题，这也就导致了近些年来如何采用自动化技术检测配电故障成为了一个热门研究话题。但是目前我国大多数配电网对此技术的应用能力并不强，主要体现在可靠性和准确性不佳，所以我们应将精力放在选线方法的研究上[2]。另外在当前形势下电缆的市场价格逐渐降低，我国城镇化政策逐渐落实，导致了电缆的应用量和线缆混合应用数量大幅攀升，进一步加大了配电网线路的设计问题，增大了困难性，提高线缆选择的要求。综上所述，我国目前在电路故障与设计方面虽然有丰厚的成果，但是仍然有较多的问题值得深入分析，在如何解决故障的领域中加大研究力度。

1 频点信息的提取方法概述

做好选线工作首先就要做好参数识别，第一步就是要辨识信号，要通过信号当中频点信息来分析出故障问题，这也是本文的选线方法中的核心。世界范围内比较常见的方法是矩阵束法、傅里叶变换法、Hilbert-Huang变换法、Prony算法等等形式[3]。

在上述的方法当中，傅里叶变换法是最为传统的算法，但是这种方法的缺点也比较明显，容易出现较大的算法误差，最终导致栅栏效应的出现，从而在构建信号时出现频谱泄漏；Prony算法也往往有较大的运算误差，在处理信号时可能导致出现较大的虚假模态，并且运用这种方法还容易导致信号被噪声干扰等问题，也存在泄露误差的可能；Hilbert-Huang变换法有着诸多优点，其中最明显的优点是能够捕捉信号的瞬时状态，但是这种方法也有着容易漏辨的明显问题；矩阵束算法是一种较为先进的算法，这种算法的优点是不存在漏辨或者泄露误差、频谱泄漏的问题，并且这种方法还有着复杂程度低，不容易被噪声干扰的优点。

2 基于奇异熵定阶的矩阵束算法

将衰减指数记为n个，其线性表达式为[3]：

式中：y(t)记为响应参数；y0(t)为信号：ε(t)为噪声；si为振荡，另有式si=-αi+jωi，其中：αi记为衰减程度；ωi为角幅度；Ri为第i个振荡模态的复幅值，且可以认为Ri的相角等于相应信号与该模态的相角差。

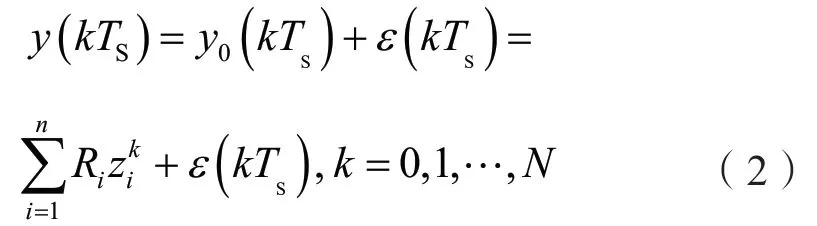
式中：Ts记为采集信号时间；N是采样点数。

将上述(2)式中角频率ωi、模态复幅值Ri、衰减因子αi以及模态阶数n提出模态辨识的概念。每当电力系统运行时出现故障，在采集信号时要考虑抗噪声干扰，还要筛选故障信号当中的衰减非整次数谐波与非周期量，所以在式(2)中，ε(kTs)≠0。下文将对模态辨识的问题进行简单描述。

要想计算模态阶数n，应用噪声信号y(kTs)构造Hankel矩阵Y：

梅赛德斯-奔驰新一代C级轿车让我有机会感受到了德国豪华汽车品牌的最新科技成果，也让我领略到了C级轿车销售火爆的真正原因。

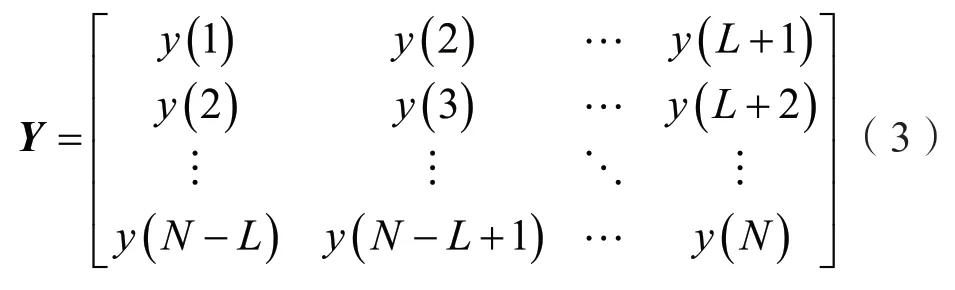
式中，适当选择参数L可以帮助抗噪声，计算zi的方差，计算束的参数范围，一般是N/3-N/2，Hankel矩阵Y的阶数为(N-L)×(L+1)[4]。

将Y分解，有：

上述式中，U和V阶数为(N-L)和(L+1)；Σ阶数(N-L)×(L+1)，Y奇异值产生σi且降序排列，满足σ1≥σ2≥…≥σm。

令m=min{N-L,L+1}，可以构建奇异普序列βi，其公式为：

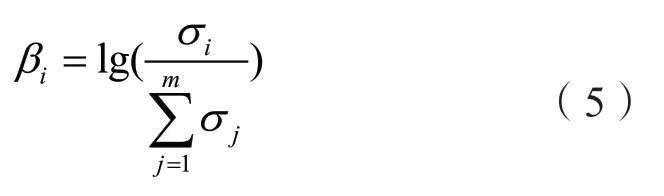
本方法的优势在于可以通过奇异熵的数值来得到信号的饱和强度，将奇异熵增量设为i阶：

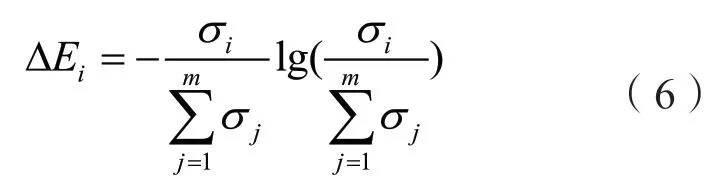
信号中有效信息比例较高时，ΔEi会明显发生值的改变，进入有界值。然后在ΔEi当中找到拐点，与其相对的i值为模态阶数n，在拐点当中由于误差的原因会产生奇异熵增量，这一部分数值应完全忽略，所以奇异熵增量在信号噪声较大的背景下可以帮助捕捉有效信号，并且该方法有助于确定模态阶数n。

首先确定n的值，在矩阵Σ中列出前n列构成阵Σ'：

从式(7)中可知，矩阵Σ'的阶数为(N-L)×n，这当中的前n行指的是n阶对角阵，该对角阵的含义是对角元素为矩阵Y的前n个奇异值，此外的数值均为0。这样就可以以该矩阵来分析过滤噪声，加强信号的辨识度。

利用矩阵Σ'来构造两个Hankel矩阵，分别是Y1和Y2，该矩阵和原本的Y相比噪声有所降低，两矩阵式为：

在上述式(8)和式(9)中，首先先从V中取出前n列构成矩阵V'，再从矩阵V'中取出前L行构成矩阵V1，取出后L行构成矩阵V2。显然，V1和V2的阶数均为L×n，Y1和Y2的阶数均为(N-L)×L。

Y1和Y2当中的元素为过滤噪声之后的参数，即上述式当中的y0(t)构成。将式（8）和式（9）展开有：

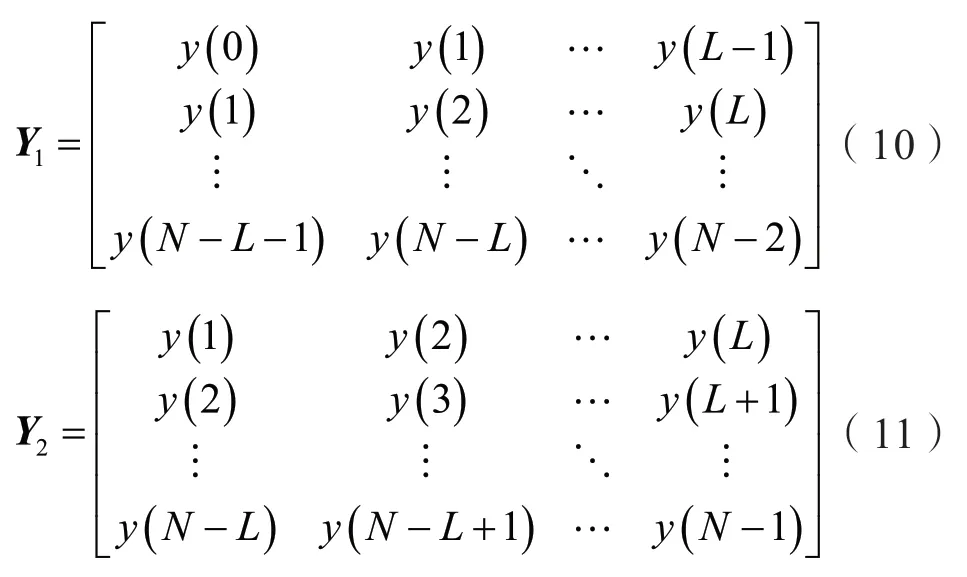
由Y1和Y2构造矩阵束Y2-λY1，并将y0(kTs)=代入整理得：

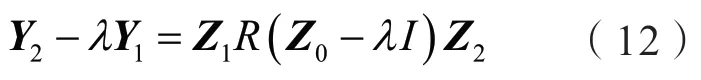
式中，

根据上述式（12）我们可知，通过数值λ可以确定矩阵束Y2-λY1的秩，也就是说当λ不是矩阵Z0的对角元素zi时，其秩为Z0的阶数；而当λ等于某一个对角元素zi时，矩阵Z0-λI的第i行元素为零，消去该行，则矩阵束Y2-λY1，的秩与之前相比，其值减1。因此，矩阵Z0的对角元素可以视为矩阵束Y2-λY1，的广义特征值。

图1所示为本文所介绍的奇异熵增量与矩阵束算法结合的原理和运算过程的简介，同时也是上文当中介绍的算法的图示流程[5]。

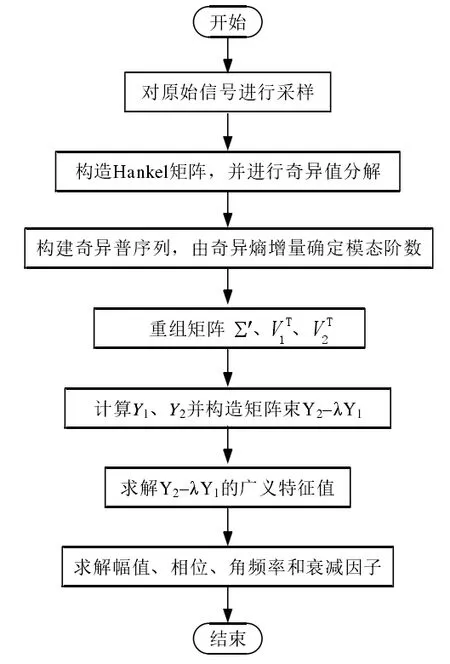
图1 奇异熵矩阵束算法的流程

3 算例分析

为了测试奇异熵增量结合矩阵束这种方法的准确度和真实性，首先列出一个衰减震荡序列，如式（17）所示，通过此式来计算出该方法的辨识能力：

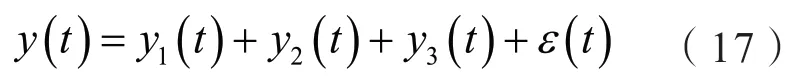
式中，y1(t)是工频信号；y2(t)是含有3次谐波的信号；y3(t)是含有非整数次谐波的信号；ε(t)为白噪声信号。上述信号表达列举的式为：

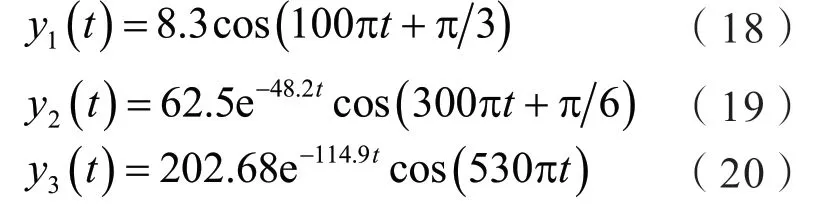
通过上述算式最终可得到的信号y(t)并非周期性信号。利用奇异熵定阶矩阵算法在不同的数据窗和采用频率的情况下进行总结分析，最终得到的分析统计数据如表1所示。在该计算当中，衰减因子、相位的误差均为绝对误差。

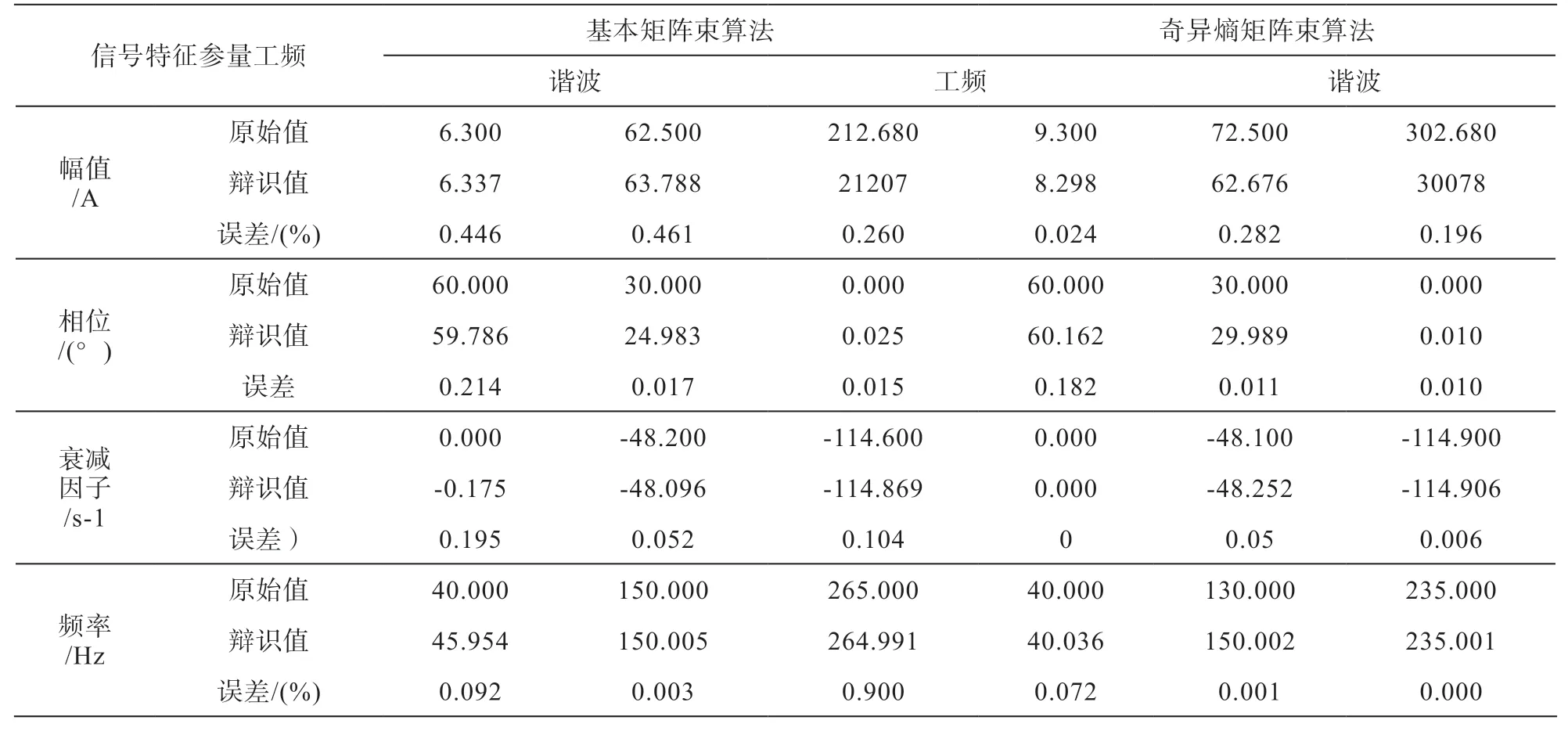
表1 两种算法的辨识结果对比

依照表1当中统计结果我们可以得知，信号当中的噪声幅度越大，比例越高，则奇异熵矩阵算法对信号特征的提取和捕捉的效果就越是精准。所以该方法既能降低运算的复杂性，又能降低虚假模态出现的可能。

4 结束语

本文主要介绍了奇异熵定阶的矩阵束算法来对频点信息进行提取，为了获得更加准确的模态阶数，在原始的矩阵束算法的基础之上提出了改进后算法的流程图，并且还提供了仿真计算例，验证本文的计算方法时候有效。