传感器故障检测与隔离算法研究
2022-09-15王兵见陈麒元
王兵见,陈 可,陈麒元
(1.交通运输部公路科学研究院,北京市 100088;2.天津市政工程设计研究总院有限公司,天津市 300000)
0 引 言
桥梁结构安全监测系统自身及其监测对象——桥梁结构都是复杂的非线性系统。该系统面对的挑战一方面是如何对庞大且丰富的监测数据进行误差处理,提高观测数据的置信度;另一方面是如何对这些数据进行分析,提取出与结构正常使用和承载能力状态有关的本征响应和发展规律,并基于多源数据来诊断桥梁的健康状态,进行科学预警。由于传感器采集的监测信息格式复杂、信息量大,如果不能有效地对这些数据进行处理,将影响评估的准确性,产生错误预警信息或漏报预警,从而导致不必要的交通阻断或者是结构失效,造成灾难性后果。
1 gpICA基本原理
由Herault等[1]于1985年提出的独立元分析(Independent Component Analysis,ICA)是一种未知源信号提取方法,已成功应用于信号处理、生物工程、医学图像、语音增强、遥感和数据挖掘等领域。ICA算法无需任何训练数据或这些信号的先验知识即可估计未知源。初出的简单的线性独立元模型仅在线性环境中有效工作[2],常规非线性独立元分析存在求解复杂和解的非唯一性等问题[3],因而研究人员聚焦于在常规模型中引入约束,形成子模型,以寻求解的唯一性。
近些年发展了许多基于线性独立元分析的故障检测技术,但是简单的线性独立分量分析算法仅在线性混合环境中有效工作。
桥梁系统是复杂的非线性系统,简单的线性独立元分析方法无法准确检测出SHM系统中的传感器故障。Nguyan等[4]提出一种几何后非线性独立元分析方法(gpICA)。该方法可以分为2个阶段:第一阶段,利用几何后非线性(PNL)算法对采集的数据进行线性化;第二阶段,通过快速独立元分析(FastICA)进行线性分离。该方法从多维空间的角度来考虑非线性盲源分离的问题,在多维空间中,非线性混合信号的三维图形是一个曲面,而混合信号为线性时,三维图形是一个平面。因此,将非线性混合转变为线性混合的目标就变成将一个曲面变换为一个平面的过程。
1.1 几何P NL混合模型
gpICA方法包括2个阶段:线性化阶段、线性分离阶段。几何PNL算法即对源信号完成线性转化。几何PNL模型混合和解混的过程见图1。
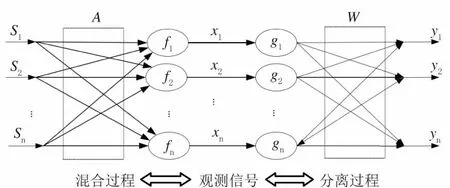
图1 几何P NL混合模型
几何PNL模型混合和解混过程可以表示为:
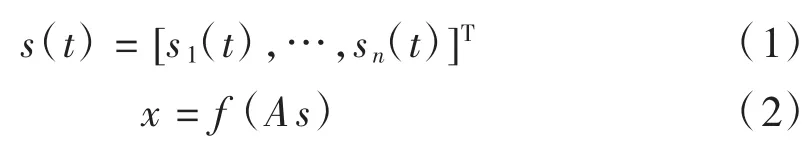
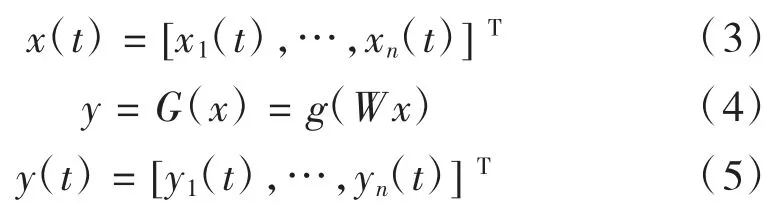
式(1)中:s为n个未知源信号。式(2)中:A为混合矩阵;f为非线性函数,代表非线性混合过程。式(3)中:x为混合信号,即传感器所得到的实际数据。为了估计源信号s,需要建立一个称为分离系统的逆系统,如式(4)所示,其中g是f的非线性反函数;W是A的逆矩阵,代表线性解混过程。式(5)中:y是s的估计值。
几何PNL算法的基本思想:在多维空间中,线性混合可以由平面表示,而非线性混合通常可以由曲面表示,所以非线性转化为线性即将曲面转化为平面。几何PNL算法的技术路线见图2。

图2 几何P NL算法的技术路线图
1.2 快速独立元分析(Fas tICA)
FastICA算法,又称固定点算法,是一种快速寻优迭代算法,与普通的神经网络算法不同的是这种算法采用了批处理的方式,即在每一步迭代中有大量的样本数据参与运算。目前算法有基于峭度、基于似然最大、基于负熵最大等形式,本文采用的是基于负熵最大的算法。
根据中心极限定理,1组均值和方差为同一数量级的随机变量共同作用的结果必接近于高斯分布。因此,在分离过程中,可通过对分离结果的非高斯性度量来表示分离结果间的相互独立性,当非高斯性度量达到最大时,则表明已完成对各独立分量的分离。由信息论理论可知:在所有等方差的随机变量中,高斯变量的熵最大,因而可以利用熵来度量非高斯性,常用熵的修正形式,即负熵来度量。
负熵Ng(Y)的定义为:
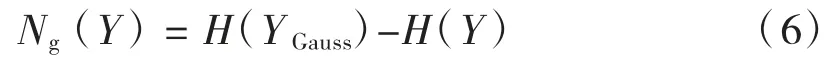
式中:H(YGauss)是一与Y具有相同方差的高斯随机变量;H(·)为随机变量的微分熵。
在源函数未知的情况下,无法知道Y的概率密度,常采用以下近似公式进行估计:
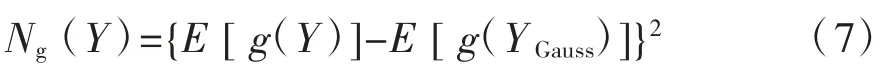
式中:E(·)为均值运算;g(·)为非线性函数,可取g1(y)=tanh(a1y),或g2(y)=yexp(-y2/2),g3(y)=y3等非线性函数,这里,1≤a1≤2,通常取a1=1。
简化后就可以得到FastICA算法的迭代公式:
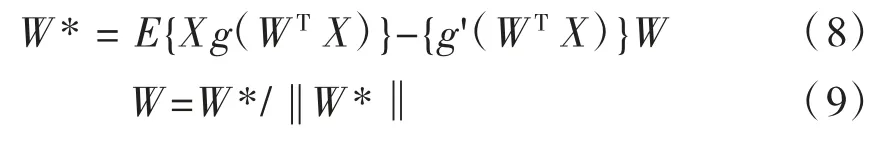
式中:W*为W的新值;W为分离矩阵。
2 基于gpICA的传感器故障检测与隔离
2.1 传感器故障数学模型
国外学者Kulla[5]总结了固定偏差、线性偏差、恒增益、精度下降、卡死、白噪声卡死和零线漂移7种监测数据失效类型。固定偏差、线性偏差、恒增益和精度退化通常称为软故障,其中传感器部分失效;卡死、白噪声卡死和零线漂移3种故障为完全故障,通常称为硬故障。
2.2 基于gpICA的传感器故障检测
通过计算每个主元的无穷范数的大小排序,选取d个主元,则可以得到Wd(选取d个W的主元行)和We(W去除Wd剩余的矩阵)。对于在某一时刻新的采样数据xnew,可以计算独立向量[6]:
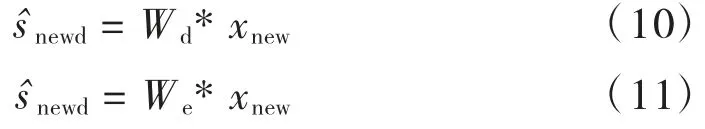
gpICA基于如下3个统计量进行故障检测[7]:统计量I2、I2e和SPE。其中I2用来表征模型内部的变化;SPE用来表征模型外残差的变化;当选择的独立元个数不恰当时,I2e能够补偿选择的误差。通过核密度估计法确定其阈值,当超过阈值时即传感器出现故障。3个统计量为:
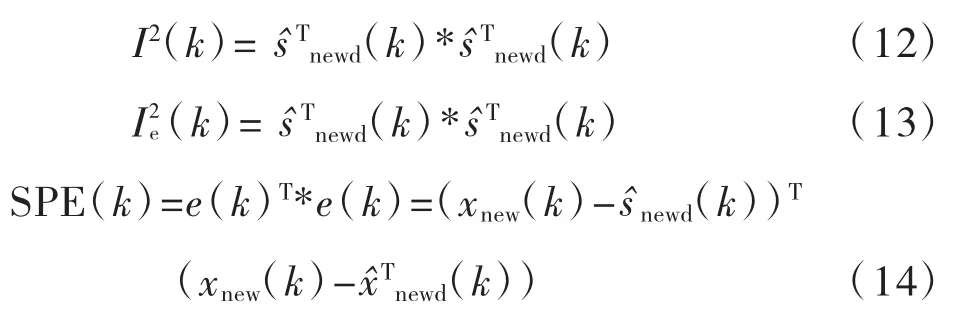
2.3 基于gpICA的传感器故障隔离
在gpICA中,用下面的公式表征对监控统计量的贡献:
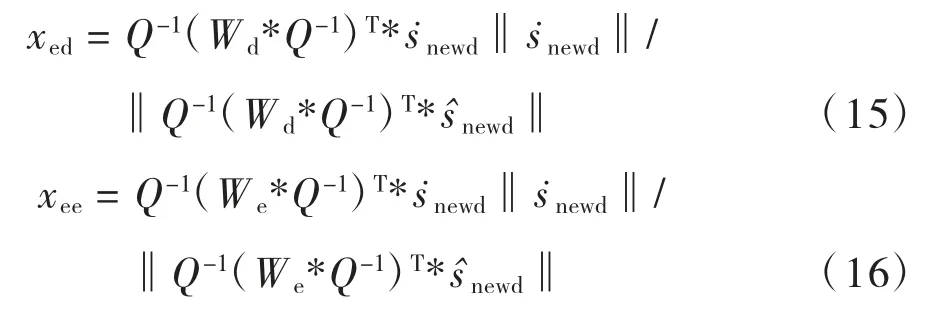
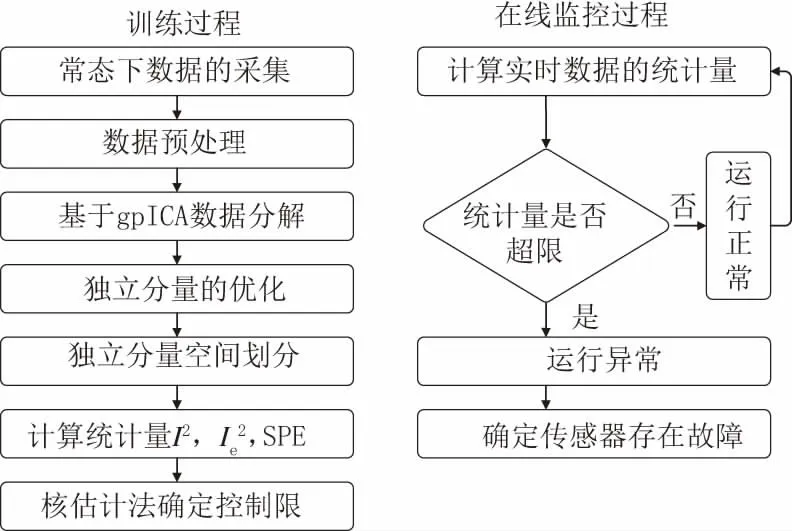
图3 故障检测流程图
式中:Q-1为矩阵求逆。
同样的方法可以得到变量对SPE的贡献。
3 算例分析
某3跨连续梁,弹性模量E=3×1010N/m2,泊松比μ=0.3,密度ρ=2 500 kg/m3;模型尺寸为梁长80 m,截面为矩形,尺寸为0.6 m×0.6 m。将3跨连续梁均分为80个单元,即每个单元长度为1 m。采用随机荷载作为连续梁的激励,使用Newmark-β法计算连续梁的加速度时程响应。假设加速度传感器布设在距离桥梁左端支座6 m、12 m、30 m、40 m处,分别编号为1、2、3、4,如图4所示。
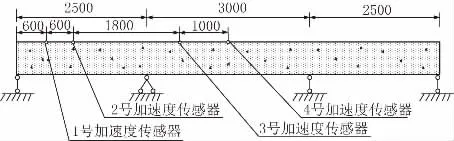
图4 传感器布置图(单位:cm)
3.1 故障数据工况模拟
在实际情况中,很多个传感器同时发生故障的概率很小,所以仅讨论1个传感器发生故障的情况。试验过程中假设结构完好,仅传感器发生故障。工况1为2号传感器发生线性偏差故障的情况;工况2为3号传感器发生恒增益故障的情况。传感器工况见表1。
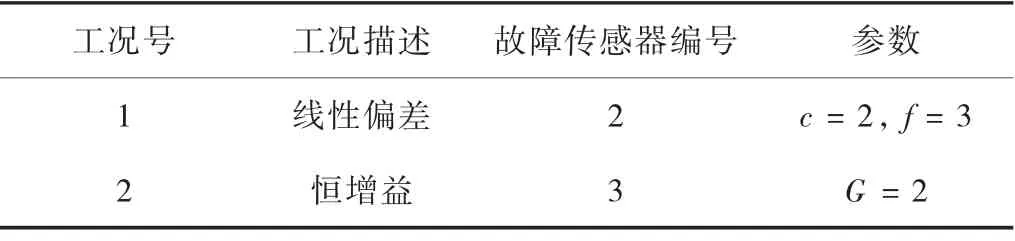
表1 传感器工况
3.2 基于gpICA的故障检测
采用MATLAB软件,首先生成100条随机荷载作为激励施加于结构。其中前50条结构响应数据用于ICA训练;第51至100条分别用于数据训练后的自动检测传感器故障。传感器故障检测时,不需要补偿误差,通过I2和SPE统计量即可准确检测传感器故障。
在工况1下,经ICA检验后,其I2统计量和SPE统计量结果见图5,其中细直线(y=0附近的直线)为各统计量置信度α=99%的阈值。由图5可知:I2统计量大部分的点均已超限,超限率为80%;SPE统计量均已超限(其中表示“SPE统计量控制限”的直线与y=0坐标重合)。因此,可以判断该过程中存在故障。
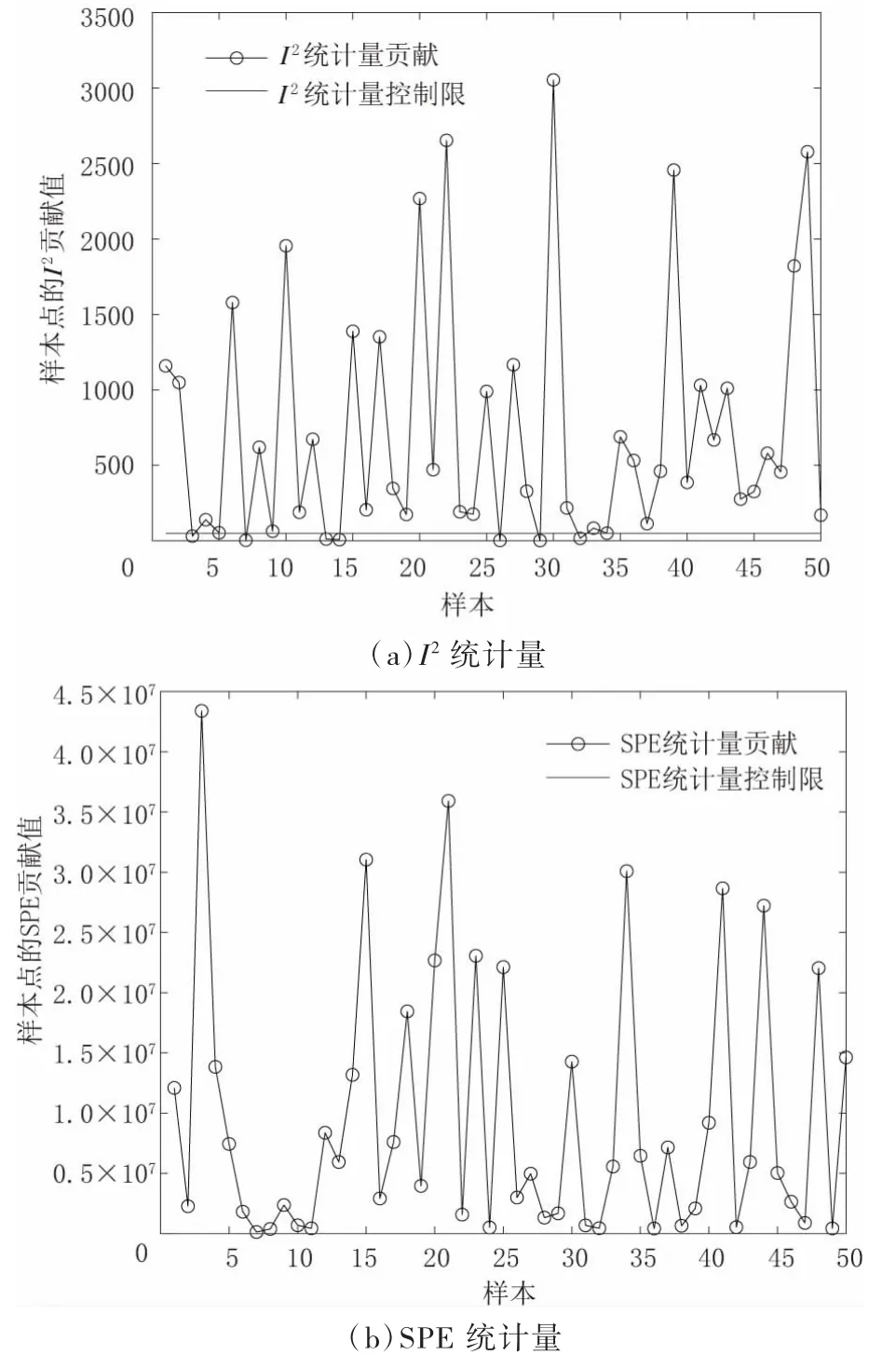
图5 工况1下ICA检验统计量
在工况2下,经ICA检验后,其I2统计量与SPE统计量结果见图6,其中细直线为各统计量置信度α=99%的阈值。由图6可知,虽然SPE统计量超限不明显,但I2统计量所有的点均已超限,超限率为100%,因此可以判断该过程中存在故障。
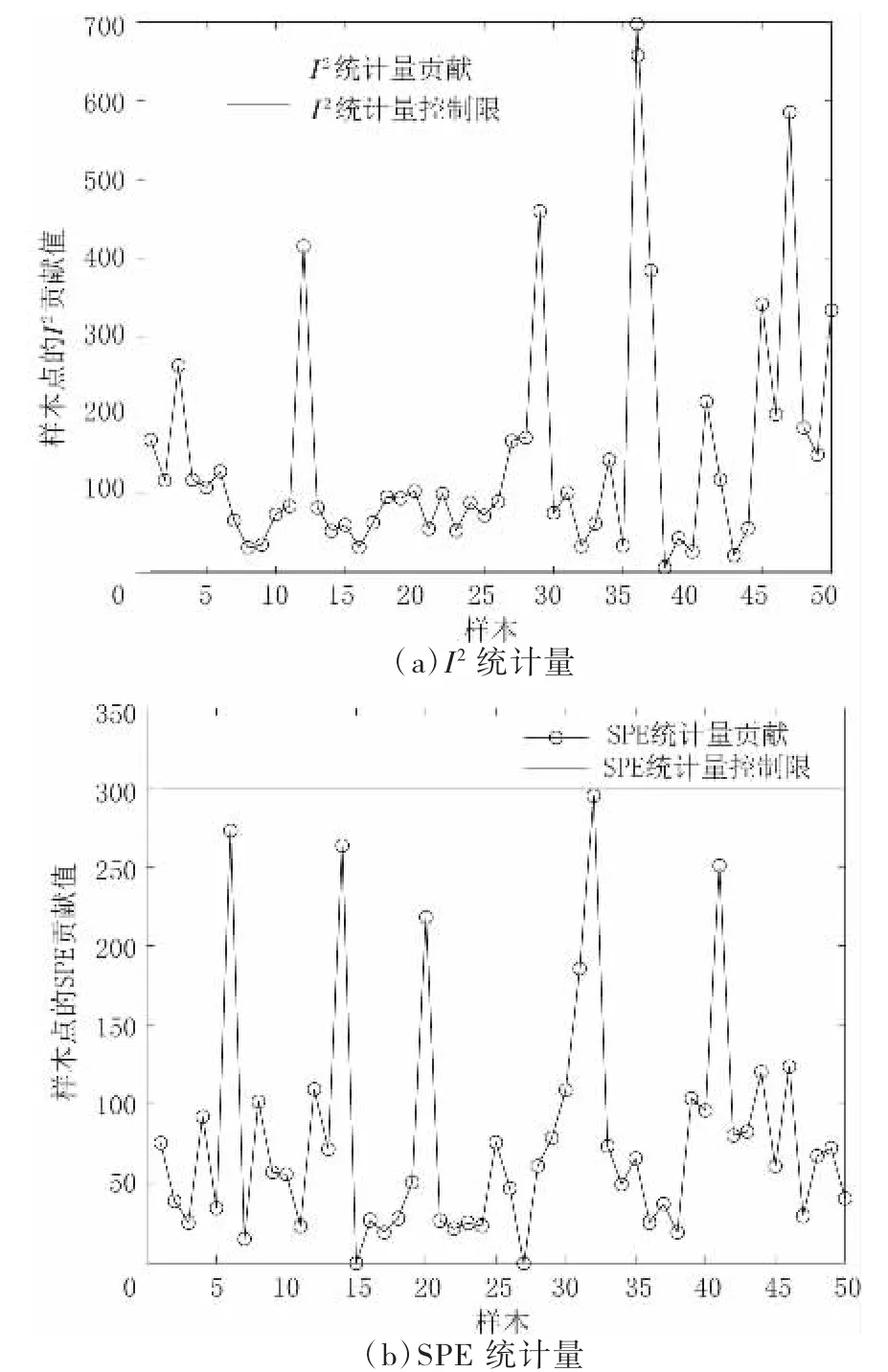
图6 工况2下ICA检验统计量
3.3 基于gpICA的故障隔离
传感器故障隔离时,共模拟10个传感器,布设在距离桥梁左端支座6 m、12 m、18 m、32 m、40 m、50 m、58 m、64 m、70 m和76 m处,编号为1~10。
故障传感器布置图见图7。
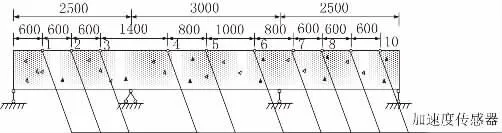
图7 故障传感器布置图(单位:cm)
设置工况1,仅1号传感器存在故障,其他传感器均正常。图8为传感器变量对I2、、SPE统计量的贡献值,可以看出所有贡献统计量均是1号传感器最高,可定位1号传感器为故障传感器。
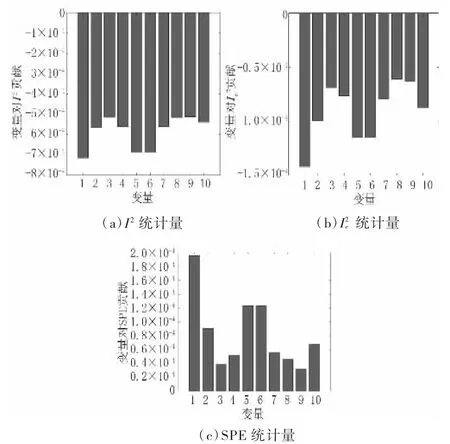
图8 传感器变量对I2、I2e、S P E统计量的贡献值
4 结语
本文提出了一种基于几何后非线性独立元分析方法(gpICA)的传感器故障检测与隔离算法。通过引入几何后非线性混合模型,将非线性监测数据转化为线性数据,再利用快速独立元分析(FastICA)方法对监控统计量进行计算。基于监控统计量与阈值的比较来实现传感器故障检测,通过计算监测数据对监控统计量的贡献度,得以确定具体故障传感器。最终通过MATLAB软件进行数值模拟,实现了模拟故障传感器的检测和隔离。该算法相比传统的线性ICA故障检测具有更高的故障检测率,更适用于桥梁健康监测系统的故障检测与隔离。
