多振型反应谱法分析减隔震桥梁

朱 锋

（北京迈达斯技术有限公司，北京市 100073）

0 引 言

反应谱法是一种拟动力分析方法，本质依然是静力法，理论上不具备分析边界非线性性能的能力。但其由于分析效率高，且荷载（作用）明确，依然是桥梁抗震分析的主要分析手段。针对减隔震桥梁，新规范通过迭代求解支座等效刚度及全桥阻尼比，并同步修正反应谱谱值，避免了时程分析的复杂性的同时，极大地提高了减隔震桥梁的设计效率。

1 工程概况

本桥位于某高速公路上，跨度布置为两联3×32 m。上部结构采用预应力混凝土连续箱梁，梁高1.6 m，主梁采用单箱三室结构。下部结构采用矩形桥墩，其中中墩采用1.8 m×1.8 m断面，交接墩采用1.3 m×1.6 m断面；中墩处不设盖梁，交接墩处设置盖梁。支座采用摩擦摆支座。下部基础采用桩基接承台基础，每个桥墩下设4根钻孔灌注桩，桩径1.5 m，各墩桩长均为50 m。

本桥地震相关控制指标为：地震分区特征周期0.4 s，场地类别Ⅱ类，抗震设防烈度Ⅷ度（0.2g）。

本次分析采用MidasCivil程序（版本号2020v2.1），共建立梁单元587个、边界480个。桩基础根据土体比例系数采用弹性连续梁理论建立。计算模型简图如图1所示。

图1 计算模型简图

2 多振型反应谱法分析

2.1 迭代思路

由于减隔震支座的刚度不是线性刚度（定值），而反应谱分析方法本身无法进行变刚度计算，故采用多振型反应谱法进行减隔震桥梁分析需要进行迭代计算。主要迭代思路在《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）中有明确的说明，在此不再赘述。其核心思想是根据每次迭代步骤计算所得的支座位移计算各支座的等效刚度和全桥等效阻尼比。上述等效刚度作为下次计算支座的线性刚度，全桥等效阻尼比作为下次计算所需谱值的相关参数。特别需要注意的是，全桥阻尼比计算后，新的迭代步骤所取谱值分为两部分。第一部分为阻尼比为5%计算所得谱值，第二部分谱值根据上次迭代计算所得全桥阻尼比算得。两部分的分割点为上次计算所得桥梁基本周期的0.8倍。全桥等效阻尼比和等效刚度的计算公式如下所示[1]。

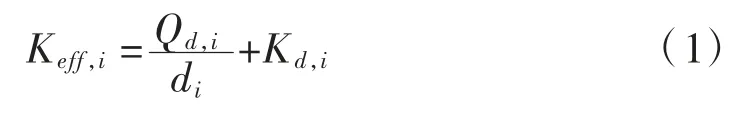
式中：Keff，i为第i个桥墩、桥台上的减隔震支座的等效刚度，kN/m；Qd，i为第i个桥墩、桥台上的减隔震支座的特征强度，kN；di为第i个桥墩、桥台上的减隔震支座的水平位移，m；Kd，i为第i个桥墩、桥台上的减隔震支座的屈服后刚度，kN/m。

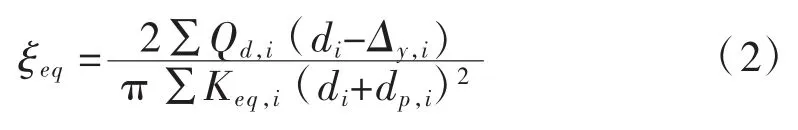
式中：ξeq为减隔震桥梁的全桥阻尼比；Δy，i为第i个桥墩、桥台上的减隔震支座的屈服位移，m；Keq，i为第i个桥墩、桥台与其上减隔震支座等效弹簧串联后的组合刚度值，kN/m；dp，i为每个桥墩、桥台顶部的水平位移。

2.2 迭代数据整理

第一次计算支座刚度取屈服前刚度，全桥阻尼比取0.05。据此计算所得支座位移及后续计算结果见表1。

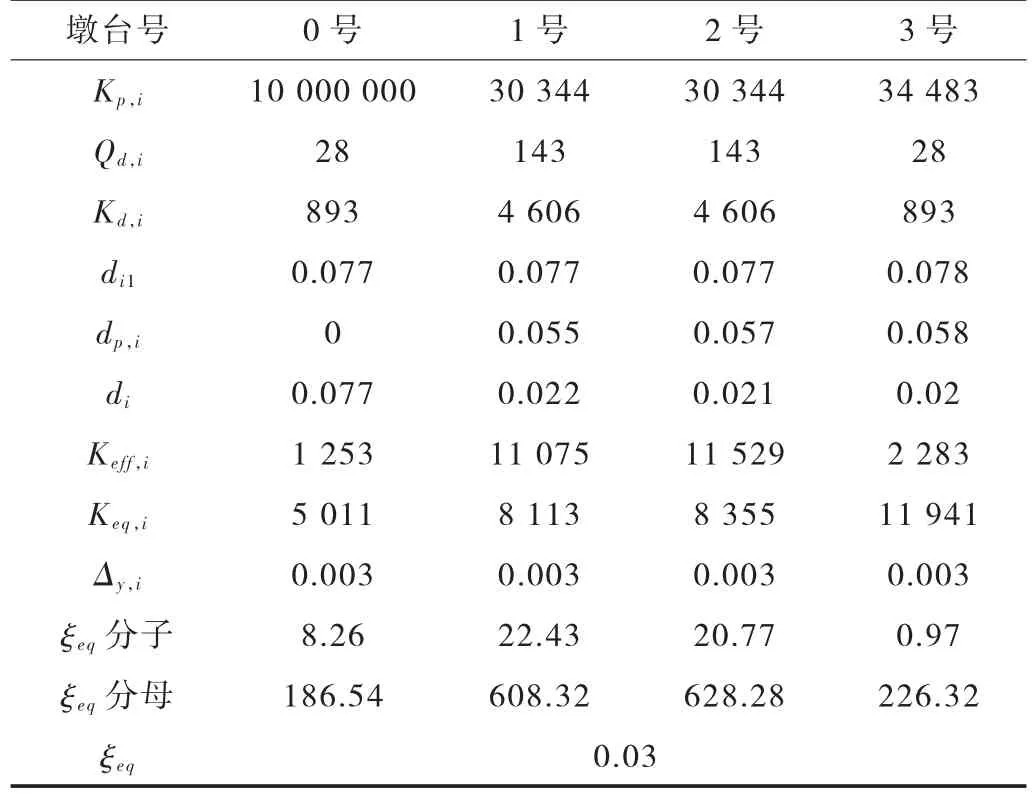
表1 第一次迭代计算 单位：kN/m

根据规范迭代思路，迭代5次后相关参数见表2。较第4次迭代计算所得支座位移，各墩台位置均小于规范规定两次迭代位移差在3%以内的要求。

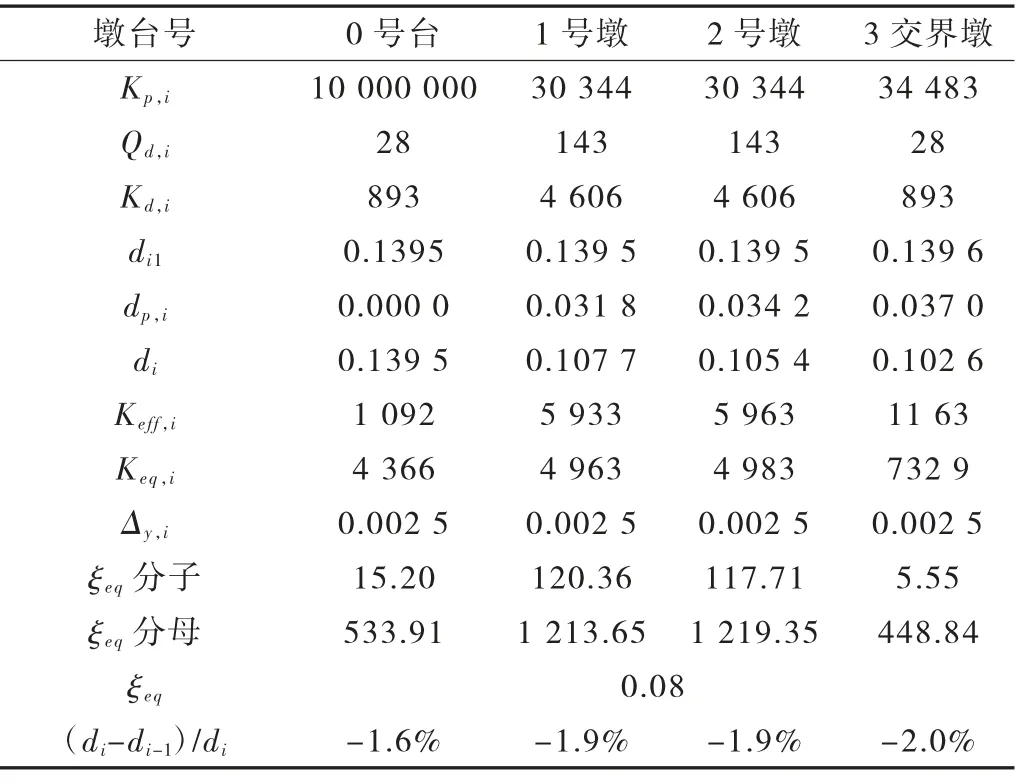
表2 第五次迭代结果 单位：kN/m

上述表格均为支座等效刚度的计算过程，迭代过程中还需要不断修正每次计算所取用的反应谱值。表3为5次迭代中反应谱值计算所需相关参数的变化情况。

表3 反应谱值计算参数 单位：s

3 与非线性时程分析法的比较

3.1 人工拟合地震波

时程分析与反应谱分析的较大不同是荷载（作用）的来源不同。反应谱分析规范中有明确的谱值计算方法，而时程分析需要做地震安全性评价或者人工拟合地震波。本项目未做安评，故采用人工拟合地震波的方式取用地震波。人工拟合地震波根据《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）的相关条文规定必须满足两条要求,地震波转换为反应谱后与设计谱的相对误差必须小于5%或绝对误差小于0.1。按照上述要求，本项目选取地震波如图2所示。地震波持续时间为20 s，最大加速度为0.259 4g。

图2 地震波时程数据（单位：m/s 2）

3.2 迭代支座阻尼比及刚度

时程分析可以有效地计算减隔震支座的非线性特性。与反应谱分析不同，时程分析结构的阻尼特性也可以通过阻尼矩阵体现。计算结果可以得到如图3所示的减隔震支座真实滞回曲线。

图3 地震波时程数据

时程分析阻尼考虑方法一般分为应变能因子法和瑞丽阻尼法。对于减隔震桥梁，由于不同振型的阻尼比严格意义上是不同的，此值也很难精确计算，故采用应变能因子法更为便利。

应变能因子法计算时需要输入结构不同部分的阻尼比。本例除减隔震支座，其余部分阻尼比均为0.05，减隔震支座的阻尼比通过迭代计算得到。每次迭代支座阻尼比根据计算所得支座位移通过《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）的相关公式计算得到。与此同时，支座的等效刚度也在迭代中予以修正，等效刚度的计算方法为本次支座计算最大位移处剪力与位移的比值。

第一次计算支座的刚度取初始刚度，支座阻尼比取0.05。据此计算所得支座位移以及等效阻尼比见表4。

表4 第一次迭代计算结果 单位：kN/m

根据上述支座位移计算所得减隔震支座等效刚度与等效阻尼比，下次迭代所得位移及阻尼比见表5。

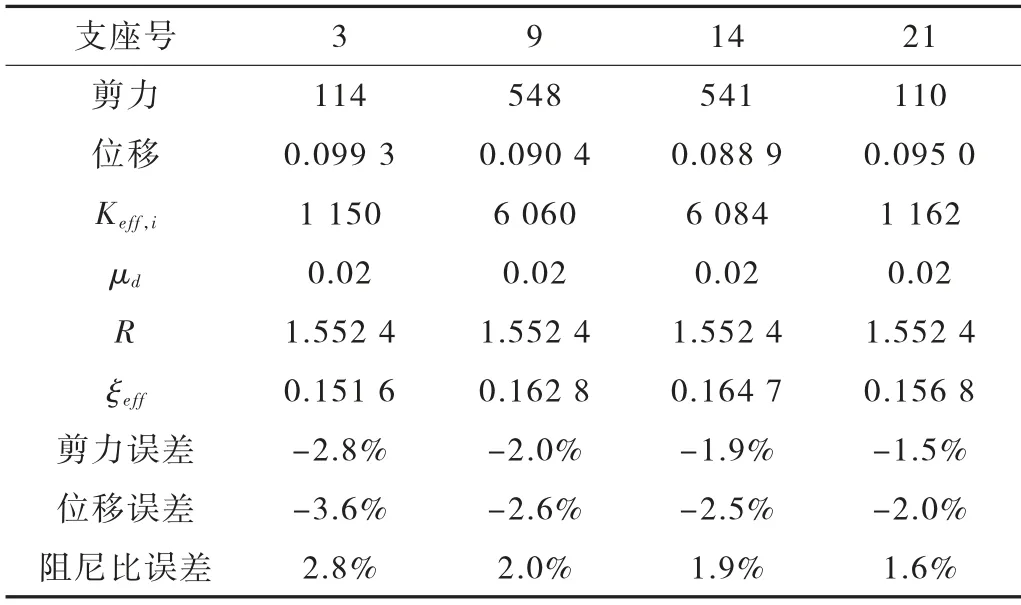
表5 第二次迭代计算结果 单位：kN/m

通过上述计算可知，阻尼比的迭代收敛速度是非常快的，最终对比也将以第二次计算所得结果与反应谱结果进行比较。

3.3 时程与反应谱结果对比

反应谱与时程本质上是两种不同的方法计算同一结构，其最终效应由于受到地震波与反应谱作用不同，线性近似计算与非线性直接求解动力微分方程的方法不同，最终结果也必然存在差异。本例基于规范给出的迭代算法，并自拟地震波，经计算后支座位移与墩底弯矩两者的差异见表6、表7。

表6 支座位移对比 单位：m

表7 墩底弯矩对比 单位：kN/m

从表中不难看出，反应谱较时程结果偏大。表6中0号台结果过大的原因是模型中模拟0号桥台是将桥台本身的刚度考虑为无穷大，而其余墩台桥墩顶或盖梁顶皆有一定的位移。表中支座位移为支座顶底节点位移差，最终造成0号台支座位移较大。

4 结语

（1）多振型反应谱法作为一种简单高效的分析方法，在新规范中被引入，有效地解决了时程分析相对复杂的问题。通过本文算例演示可以发现，这种方法只需每次迭代时计算减隔震支座的有效刚度和全桥等效阻尼比即可用线性方法分析非线性问题。

（2）时程分析减隔震桥梁依然存在迭代计算的问题，阻尼计算方法可以采用应变能因子法，从本文的算例可以看出迭代的收敛速度很快。

（3）从反应谱与时程分析的比较结果看，本例中反应谱分析的结果要大于时程分析的结果，对于后续的结构设计是保守的。虽然规范中没有明确说明减隔震桥梁反应谱分析与时程分析结果的差异必须满足的合理范围，为了避免反应谱分析结果出现过于保守的情况，可自拟地震波进行时程分析，并与反应谱分析做必要的比较。