可见光通信星座整形与人工智能解调技术

蔡济帆/CAI Jifan，徐增熠/XU Zengyi，迟楠/CHI Nan

（复旦大学，中国 上海 200433）

可见光通信是一种新兴的无线通信方法，它是在可见光谱段进行数据通信的技术。中国信息通信研究院发布的《6G总体愿景与潜在关键技术》白皮书提到，可见光通信具有免授权、高保密、绿色无辐射等特点，适用于室内应用场景，可作为室内网络覆盖的有效补充。此外，可见光通信也可应用于水下通信、空间通信等特殊场景，以及医院、加油站、地下矿场等电磁敏感场景。发光二极管（LED）因其具有集照明和通信于一体的独特功能而越来越受到学者们的关注。因此，基于LED的可见光通信技术是当前全球的研究热点。

虽然可见光频段有极其丰富的频谱资源，但是目前LED可见光通信系统仍然受限于光电器件的调制带宽、非线性噪声、水下光功率快速衰减等因素。这对高速大功率可见光通信的研究和实现提出挑战。目前可见光通信的研究内容主要有两个方面：从硬件上提高调制带宽，或者利用算法对信号进行非线性补偿。其中，后者因为无须改变硬件设备而广受欢迎。例如，星座点几何整形（GS）技术可通过增加星座点之间的最小欧氏距离来减小解调时被误判的可能性，并在平均功率受限的情况下降低信号的峰均比，进而减小系统整体的非线性。ZHAO J.等提出GS-8QAM（QAM是指正交振幅调制）以改善传统8QAM的性能。由于在星间、星地和水下可见光通信中常常出现信号平均功率受限的情况，GS算法将在未来可见光通信系统中广泛应用。近年来随着深度学习技术的提升和大量运用，不断有研究借鉴相关成果以提升通信系统性能。CHEN H.等提出一种名为基于深度神经网络（DNN）的时频联合后均衡器（TFDNet）的非线性弹性学习后均衡器，该均衡器的性能优于传统的后均衡器。还有学者提出一种基于双支流异构神经网络（TTHNet）的信道仿真器，这种仿真器适用于估计水下可见光通信（UVLC）的单载波和多载波调制信道。随后，HU F.等证明了使用函数链接人工神经网络（FLANN）进行非线性补偿的优异性能。以上研究结果表明，神经网络可以替代传统通信系统中依靠公式建模的某些环节，高精度拟合非线性的映射关系。但是目前仅使用神经网络完成高速信号从波形到符号的完整解调过程的研究还相对较少。使用神经网络代替传统解调策略将极大简化系统的处理流程，降低相关硬件设备的复杂度，并且可以实现多种不同信号的解调处理。

本文提出了一种新型的几何整形编码算法，使星座点间的汉明距离达到局部最小值。这种近似于格雷编码的编码方式有很大的格雷增益，即在相同误码率的情况下具有更小的误比特率。此外，本文还使用DNN处理接收信号，代替了信号在接收端的匹配滤波、下变换、解调和解码的全过程。该技术使系统性能更加优越，它是未来可见光通信中一项很有潜力的技术。

1 技术原理与实验装置

1.1 星座点几何整形编码算法

几何整形最基本的思路就是增加星座点之间的最小欧氏距离，降低信号功率的峰均比（PAPR），其目的是减小通信系统中的码间串扰和非线性效应。增大欧氏距离可以减少星座点之间的串扰，从而降低解调时被误判的可能性。减小PAPR可以在峰值受限的情况下尽可能提高平均功率，增大星座点间的距离，提升信噪比。PAPR的计算方法如公式（1）所示。

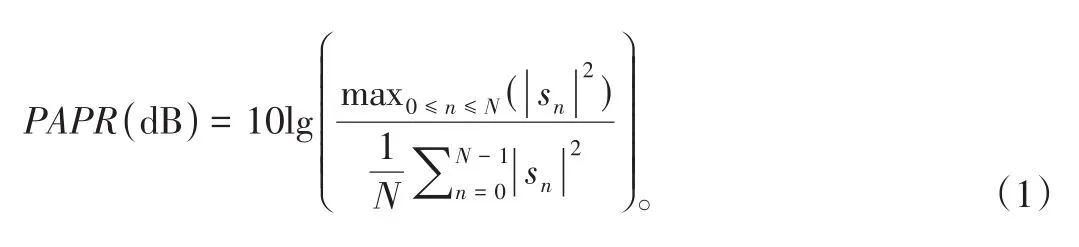
图1（a）展示了64QAM和64APSK星座点以及它们对应的编码方式。其中，64QAM采用格雷编码，而64APSK借鉴国际卫星通信标准（DVB）-S.2的排布方式，从内到外一共有4个环，每个环的星座点个数分别为4、12、20、28。由于64QAM可以满足格雷编码，且其编码已经是最优解，而几何整形64APSK无法满足格雷编码，因此我们需要使用一定的算法使其无限接近格雷编码，即汉明距离最小。由于64APSK的编码映射方式有64的阶乘种，我们不可能遍历寻找全局的最优解，因此我们选择贪婪算法寻找局部最优解，对其编码方式进行改进。首先，我们把最大的迭代次数和待训练的64APSK送入网络并初始化星座点的编码。为了简化汉明距离的计算过程，考虑到每个星座点被误判成最邻近点的概率最大，我们仅计算每个星座点和欧式距离最近点之间的汉明距离。因此在本文所提算法中，我们首先随机选择、两个星座点并将它们各自的邻居求出，即集合Q和Q。随后使用异或运算分别计算、两点此时的汉明距离并求和，记为Hd；然后将、星座点位置进行交换，计算交换后的汉明距离并求和，记为Hd。如果交换后汉明距离减小，则交换两个星座点；如果交换后汉明距离不变或增大，则不交换。根据以上算法，在经过大约2 000次迭代后，汉明距离不再减小，对应的编码结果也在图1（a）中给出。

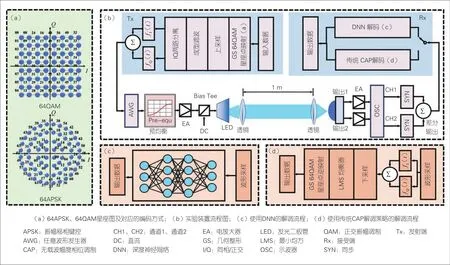
图1 可见光通信系统实验流程图

1.2 无载波幅度相位调制（CAP）解码技术

CAP是一种多维多阶的调制技术，它在20世纪70年代首先由贝尔实验室提出。采用这种调制技术，可以在有限带宽的条件下实现高频谱效率的传输。CAP在调制过程并没有和载波相乘，而是直接和两个相互正交的成型滤波器进行卷积以形成带通脉冲信号。该技术能够改变同相和正交支路的波形反应所传递的数据流，因此CAP也被称为“无载波”。

如图1所示，在发射端，二进制的数字信号首先进行阶数为的QAM格式调制以提高频谱效率，接着经过上采样、奈奎斯特滤波后被分成同相/正交（I/Q）两路。此时信号不与正余弦副载波相乘而是分别通过一对正交成型滤波器进行滤波，这是CAP与副载波调制最大的区别。这一对正交成型滤波器（也被称为希尔伯特滤波器对）通过平方根生余弦脉冲和正余弦函数分别相乘构造，是发射模块中最重要的结构。信号经过IQ分路后，与两个滤波器叠加的过程可以由式（2）给出。

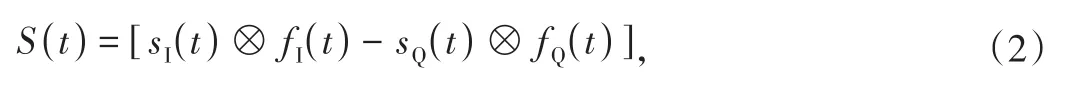
其中，()和()分别表示信号经过IQ分路后的两路正交信号。()和()表示一对正交成型滤波器，()表示最终的发射信号，符号⊗为卷积操作。

在接收端，经过信道后的光信号被PIN（P-I-N型二极管）直接探测，电信号被发送到两个和输入端完全相同的匹配滤波器中。IQ两路信号分离的过程如公式（3）—（4）所示。其中，()为接收到的波形信号，()和()表示一对匹配滤波器，()和()为输出的两路信号，它们在经过后均衡和QAM解调后便能恢复原始的发送数据。

1.3 DNN解码技术

由于神经网络拥有强大的数据处理能力，因此我们可以在接收端使用一个DNN解码器来代替传统CAP解码的所有步骤，包括IQ分路、下采样、后均衡、解调等，如图1所示。DNN的信号处理过程包括一个输入层、若干个隐藏层和一个输出层。输入波形数据并在输出处得到解调后的符号，即可完成信号的借条过程。隐藏层的结构决定了网络可以在输入和输出参数之间建立复杂的联系：神经元的连接方式决定了上一层神经元向下一层正向传播时的传播方向及加权求和。在传播至下一层后，每一个神经元都会使用特定的非线性函数进行加权和映射，以获得自身的输出。由于参数（神经元层数、每层的神经元数、非线性函数的选择等）过多，没有固定的规则来决定应该使用多少个隐藏层以及每个隐藏层应该有多少个神经元。这通常需要凭借人的调参经验、相关实验或其他先验知识来解决这个问题。

1.4 实验装置

图1展示了我们搭建的实验平台。在实验设置中，我们使用MATLAB产生64QAM和64APSK信号，然后将其加载到任意波形发生器（Tektronix AWG710B，4.2 GSa/s）中。信号首先通过前向均衡板补偿高频成分的损失，然后进入放大器（ZHL-2-8-S+）放大信号，紧接着通过一个偏置三通（ZFBT-4R2GW-FT+），为蓝光LED提供直流驱动电流。光信号在通过1 m的传输距离后由一个PIN接收机接收。接收机产生两路相反的信号，在放大、同步后相减即可得到差分信号，用以消除系统产生的共模噪声。最后我们用示波器（DSO9404A，20 GSa/s） 对信号进行采样。在离线数字信号处理方面，我们采用两种不同的方式（传统的CAP解码和深度神经网络解码）进行解码，同时将原始信息恢复出来并比较两种解码器的优劣。

2 实验与结果分析

实验的第1项任务是完成神经网络的调参。由于信号的前后码元会互相干扰，根据以往实验的经验，我们将抽头数taps设置为39，即考虑当前码元前后各19个码元的影响。因为在发射端我们对数据进行了4倍上采样，所以DNN的输入应该为156个神经元。我们使用DNN拟合星座点的I路和Q路坐标，因此DNN的输出有2个神经元。为了确定网络的隐藏层个数，我们分别测试了2层隐藏层、3层隐藏层、4层隐藏层的效果，其中每个隐藏层神经元的个数均为39，测试结果如图2（a）所示。从图中我们可以看到，3种情况的误码率（BER）都低于CAP解调，且3层隐藏层的效果最好，其次是3层，最后是2层。这是因为当隐藏层数量较少时，网络没有足够的复杂度来学习数据之间的规律；而当隐藏层数量较多时，反向传播过程中网络没有足够的梯度来寻找最优解。因此我们将隐藏层的数量设置为3。

紧接着我们需要确定3个隐藏层中每层神经元的个数。为此，我们分别测试隐藏层神经元个数在（156，156，156）、（39，39，39）和（39，78，78）下的结果，并且将其与CAP的结果作比较，如图2（b）所示。可以看出，（156，156，156）排列的BER只在非线性区低于CAP，效果最差；（39，39，39）和（39，78，78）排列的BER在所有区域都低于CAP，并且（39，78，78）的效果最好。因此，39、78、78分别为3个隐藏层的神经元个数。

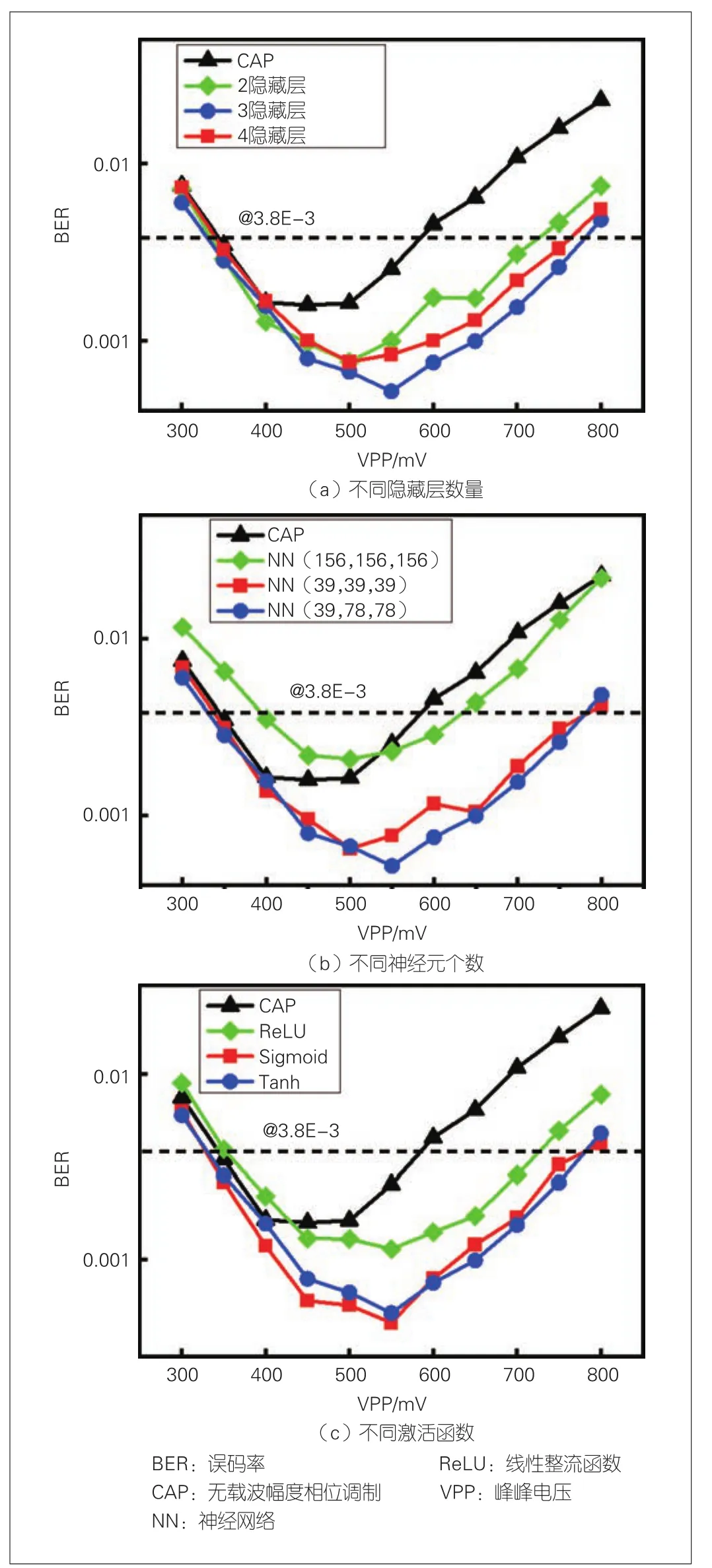
图2 不同神经网络参数得到的BER随VPP的变化曲线

在调参过程的最后，我们比较了不同非线性激活函数下网络对非线性的处理能力。我们分别测试了线性整流函数（ReLU）、Sigmoid和Tanh的效果，并将它们与CAP作比较，结果如图2（c）所示。可以看出，在峰峰电压（VPP）小于400 mV时ReLU的BER高于CAP，效果最差，而Sigmoid和Tanh在所有范围内的BER都低于CAP。因此，根据图2（c）可知，在VPP低于550 mV时，激活函数被设置为Sigmoid；在VPP高于550 mV时，激活函数被设置为Tanh。

实验的第2项内容为测试调参后网络在通信系统中的性能表现。为了能清楚地看出DNN在线性区和非线性区的处理效果，在偏置电流为150 mA的条件下，我们从300 mV到800 mV遍历驱动电压。在传统CAP解调和DNN处理下64APSK和64QAM的BER如图3所示。可以看出，无论是64QAM还是64APSK，DNN在低电压的线性区效果和CAP相似，而在高电压的非线性区，DNN的效果明显优于CAP。这说明CAP解调可以处理线性区大部分的码间串扰，而在非线性区DNN展示出了超过传统CAP解调方式的非线性处理能力。以7%冗余的前向纠错（FEC）可以工作的最高误码率作为门限（BER=3.8E-3），在使用DNN的解码后，64APSK VPP的工作区间从250 mV提升到450 mV，64QAM VPP的工作区间从220 mV提升到360 mV。同时，64APSK的性能要优于64QAM。在使用传统最小均方算法（LMS）后，64APSK的工作范围比64QAM大30 mV；在使用DNN后，64APSK的工作范围比64QAM大90 mV。

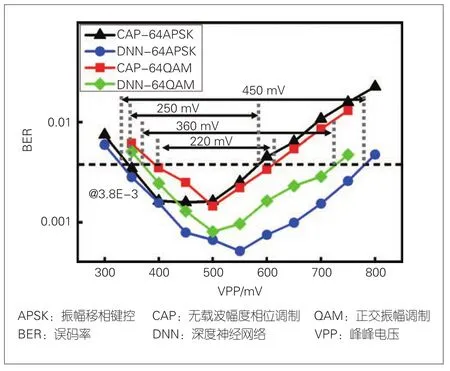
图3 CAP和DNN解码后64APSK和64QAM的BER曲线

为了更进一步地比较APSK和QAM在水下通信的效果，我们将VPP从250 mV遍历到750 mV，并将偏置电流从70 mA遍历到170 mA，同时给出BER的热力图，如图4所示。图4（a）和图4（c）分别为CAP解调后APSK和QAM的热力图。其中，白线圈出了BER等于2E-3的范围，并用以指代不同调制格式和不同解码方式下的系统工作范围。从图4可以看出，APSK的工作范围主要集中在高电流区，即高功率的非线性区，因而能承受更高电流带来的非线性效应压力。由于水下可见光功率衰减得很快，因此使用APSK进行高功率传输将会获得比QAM更大的传输距离和更高的传输容量。图4（b）和图4（d）分别是使用DNN解码处理后的BER热力图。可以看出，相比于CAP解调，APSK和QAM的工作范围得到进一步扩大，同时，工作区间向着更大电压和更大电流的方向移动。这说明我们的DNN神经网络对于高功率的非线性区域有更好的处理效果。

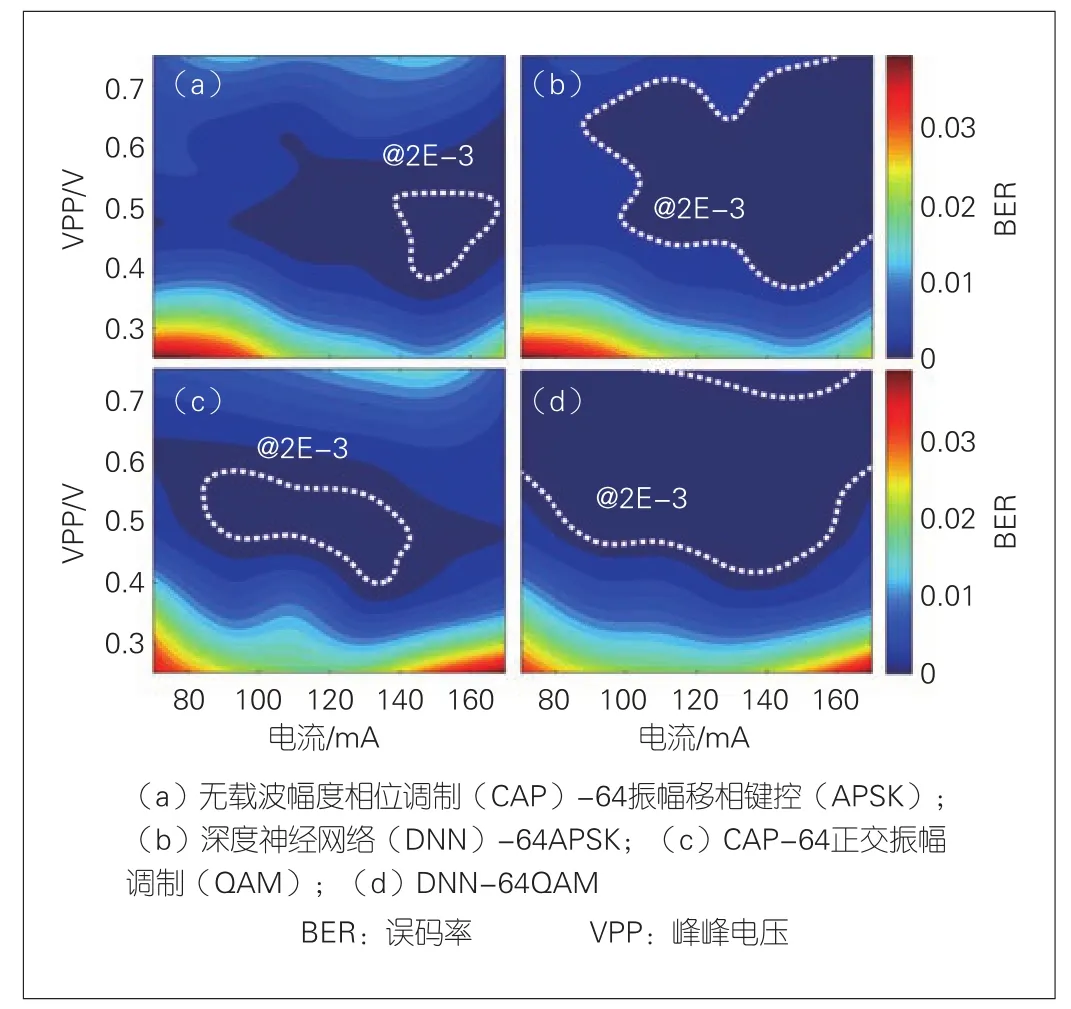
图4 不同驱动电压和偏置电流下BER的热力图

在通信性能测试的最后一项实验中，我们在驱动电压为500 mV、偏置电流为150 mA的条件下提高数据的传输速率，并以7%FEC作为门限，测试数据可以达到的最高传输速率。为了更好地观察传输效果，我们把BER转化为值。从图5中可以看出，在64APSK的调制和DNN解码下，数据的传输速率可以达到3.21 Gbit/s。它比CAP-64APSK的传输速率快了75 Mbit/s，比DNN-64QAM的传输速率快了120 Mbit/s。相比于CAP解调，DNN处理后信号的值最大可提升0.7 dB（传输速率为3.15 Gbit/s时），且64APSK的提升效果比64QAM更显著。因此DNN-64APSK最适合用于大功率的可见光通信。图5还给出了在比特率等于3.15 Gbit/s时64APSK和64QAM的星座图。

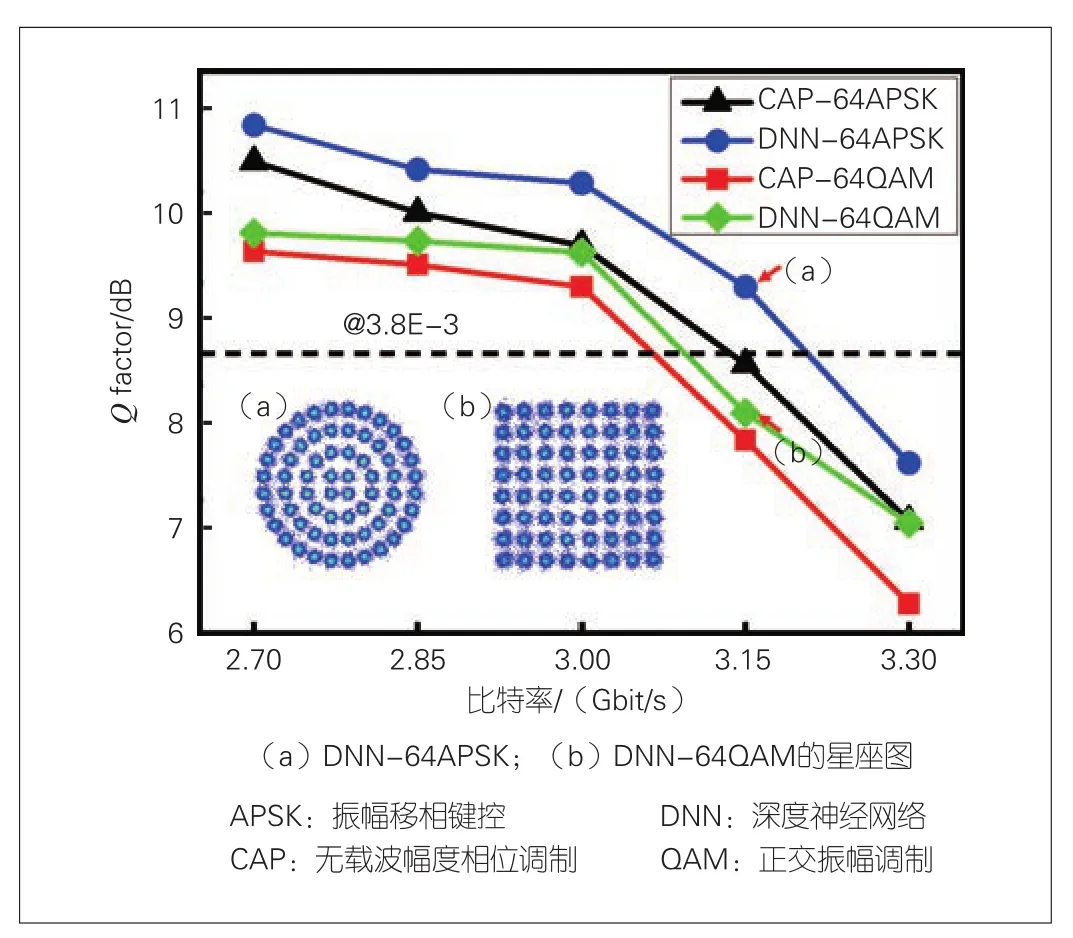
图5 Q值随比特率的变化曲线；在比特率为3.15 Gbit/s时

3 结束语

在本文中，我们提出了一种基于贪婪算法的几何整形编码方式，并使用了一个3层隐藏层的DNN神经网络作为接收端的解码器。在实验中，我们分别使用了64QAM和64APSK调制并且比较了两者在CAP解码和DNN解码下的传输效果。实验结果表明，在使用了DNN解码后，64APSK电压的工作区间从250 mV提升到450 mV，64QAM电压的工作区间从220 mV提升到360 mV。同时，APSK对偏置电流有更大的承受能力，适用于高功率传输。在传输速率上，使用64APSK调制和DNN的解码后，数据的传输速率可达到3.21 Gbit/s。它比CAP-64APSK的传输速率快75 Mbit/s，比DNN-64QAM的传输速率快120 Mbit/s。可以看出，我们使用DNN神经网络成功替代了传统通信CAP解码的下采样、后均衡、解调等全过程，并且系统性能更加优越。它是未来可见光通信中一项很有潜力和前景的技术。