振动基柔顺驱动打磨机器人的力/位混合控制研究

尤子成，王志刚，郭宇飞

(1.武汉科技大学，冶金装备及其控制教育部重点实验室，湖北武汉 430081;2.武汉科技大学，机器人与智能系统研究院，湖北武汉 430081)

0 前言

随着对机器人技术研究的不断加深，打磨机器人广泛应用于磨削加工领域。机器人打磨相比于人工打磨具有连续工作时间长、效率高等优点。通过对打磨机器人进行力控制或者位置控制可提升打磨精度，保证打磨件质量。国内外学者对机器人打磨加工的研究主要集中在打磨机制和工艺、轨迹规划、力控制算法及系统开发等几个方面。

打磨机器人不仅要求其末端打磨机构能按照预定的轨迹行走，更要求其打磨机构对加工件保持恒力打磨。目前，主要的力控制方法分为力/位混合控制与阻抗控制。这两种方法都是通过主动控制方式，使打磨机构与加工件接触时存在柔顺特性。阻抗控制是将机械臂系统建立为等效阻抗模型，当机械臂末端与环境产生接触力时或实际运动轨迹发生偏差时，阻抗模型会产生反馈信号对位置或力进行调节。力/位混合控制是将机械臂末端在笛卡尔坐标系下进行正交分解，在2个子方向上分别进行力控制和位置控制。文献[9]采用滑模控制对力进行控制，可在外界环境刚度突然发生变化的情况下保持恒力打磨。文献[10]采用模糊PID控制算法提高了接触力稳定性。

打磨机器人通常被安装在固定基座上对打磨件进行打磨，但对于大型的加工件，如飞机叶片、航天器机身、薄壁工件等，打磨机器人在打磨抛光作业时需移动打磨。然而，移动打磨会产生基础振动从而影响打磨、抛光精度，同时长时间打磨会对关节造成损伤。文献[11]在机械臂末端添加智能执行器以控制接触力，达到抑制振动的效果。文献[12]对受到振动的机械臂采取分段线性反馈控制，减少了振动造成的影响。

在打磨机器人加工过程中，机械臂末端与环境之间会产生持续性碰撞，接触力反馈回关节，从而对关节造成一定的损伤。为避免机械臂关节的损伤，在机械臂末端与电机之间添加扭簧柔顺装置即串联弹性驱动器(Series Elastic Actuators,SEA)。文献[16]中空间机器人在捕获其余航天器过程时，通过在电机与关节之间串联弹性驱动器及自抗扰控制方案，避免了关节受到冲击力。文献[17]设计了一种弹簧阻尼缓冲装置，避免关节受到载荷冲击被破坏。但添加弹簧类装置也会造成关节的振动，需对柔性关节的振动进行抑制。学者们对此进行了许多研究，奇异摄动法是重要方法之一。通过奇异摄动法可将刚柔耦合系统分为不同时间尺度的2个子系统，分别对它们设计控制器，从而实现系统的控制。文献[18]对传统SEA机械臂进行改进，采用干扰观测器提高系统的鲁棒性。文献[19]对柔性空间机械臂系统引入奇异摄动法，将系统分为快、慢2个子系统，慢变子系统采用状态观测器进行控制，快变子系统采用差值反馈法进行控制，抑制了系统的弹性振动及外部干扰。

本文作者针对打磨机器人，考虑基础振动、转动关节柔性，建立打磨机器人动力学模型。采用奇异摄动法将系统分为快、慢2个子系统，快变子系统采用速度差值反馈控制法，慢变子系统采用力/位混合控制。力/位混合控制中，力控制采用PID控制，位置控制采用神经网络鲁棒控制器控制，研究打磨机器人在基础振动的情况下，保持恒力打磨及轨迹的准确跟踪。

1 打磨机器人建模与奇异摄动模型

1.1 打磨机器人动力学模型

以柔性关节刚性臂打磨机器人为研究对象，打磨机构与机械臂末端相连，其简化模型如图1所示。柔性关节处的电机输出轴与关节部分通过线形扭簧连接，如图2所示。

图1 机械臂简化模型示意

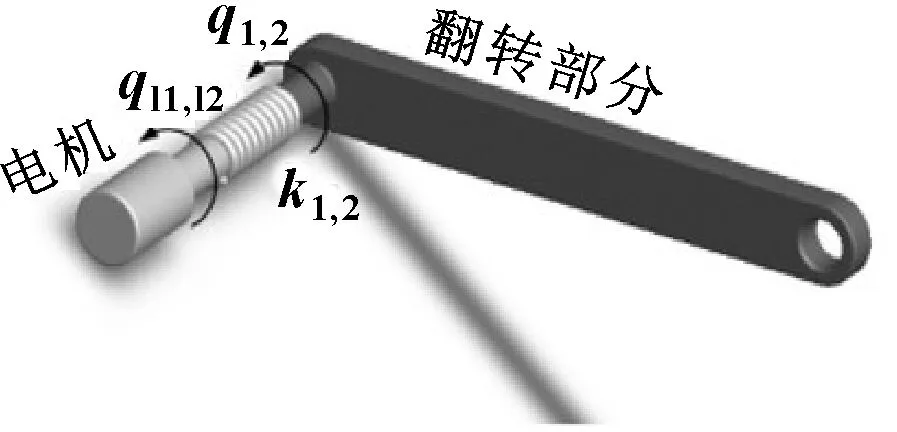
图2 柔性关节简化示意

基于以上简化模型，用拉格朗日法建立动力学方程为

(1)

其中:()为惯性矩阵；()为离心力和哥氏力矩阵；()为系统重力矩阵；为传动部分的刚度矩阵；()为转动关节柔性产生的附加惯量矩阵，也是一个正定对称矩阵；为柔性关节产生的附加坐标;为关节的角位移；为驱动力向量。各项表达式分别为

=

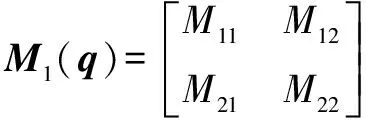
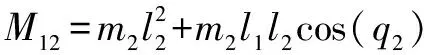
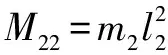
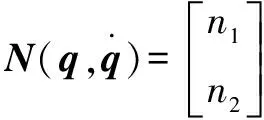
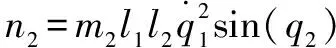
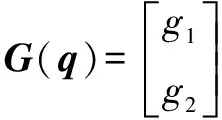
=(+)cos()+cos(+)

=cos(+)

式中：、分别为关节1和2处等效到电机轴的转动惯量。

1.2 奇异摄动模型

柔性关节的转动会引起系统的弹性振动，因而会对系统的位置控制以及力控制产生影响。所以，针对打磨机器人系统设计的控制率不仅要保持力控制和位置控制的稳定，还要抑制柔性关节所引起的振动。在系统中引入奇异摄动法，将刚柔耦合系统分解为快、慢2个时间尺度子系统，分别对这2个子系统设计控制率，最后将慢变控制率与快变控制率相加可得到系统的总控制率。

定义柔性力变量为

=(-)

(2)

引入摄动参数，定义新的刚度矩阵：

=

(3)

将柔性力变量和新刚度矩阵代入式(1)，求得系统的奇异摄动模型为

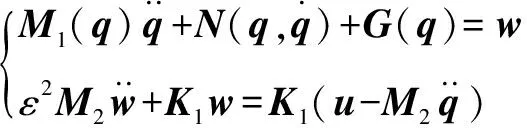
(4)

分别对奇异摄动模型中的快、慢子系统进行求解。

1.2.1 慢时变子系统

由式(4)可知，令摄动参数=0,可求得慢时变刚性系统变量为

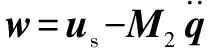
(5)

将式(5)代入式(4)中的第1个公式，可以得出慢时变子系统的动力学方程：

(6)

通过对比刚性二自由度机械臂模型，可知在不考虑柔性的前提下，慢时变子系统动力学方程与前者一致。

1.2.2 快时变子系统

将式(4)中的第1个公式进行变形得：

(7)

将式(7)代入式(4)的第2个公式，得：

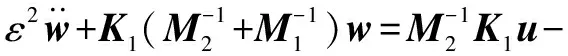
(8)

将=0代入式(8)，可得：

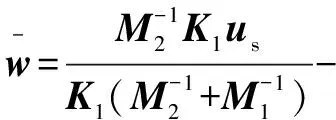
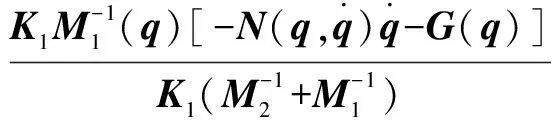
(9)

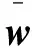
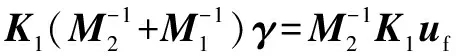
(10)

式中：=-为快时变子系统的广义控制量。

(11)

2 控制器的设计

2.1 混合控制

通过前文可知，只需将快、慢2个子系统的2个控制率相加即可得到系统的控制率：

=+

(12)

通过慢时变子系统控制率，实现打磨机器人的力控和位置控制；通过快时变子系统控制率实现柔性关节的振动抑制。混合控制器原理如图3所示。

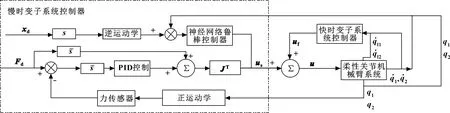
图3 打磨机器人混合控制原理

2.2 快时变子系统的控制率

分别对快、慢子系统进行设计，设计的快时变子系统的控制率为

(13)

式中：=/,为正定对角矩阵。根据关节的实际角速度与电机输出的角速度差对系统进行反馈控制，以保证系统稳定。

2.3 慢时变子系统的控制

由前述可知，采用奇异摄动法对系统进行分解，分解后的慢时变子系统与刚性系统无区别。针对打磨机器人在工作中会受到振动的影响，利用力/位混合控制对打磨机进行力控和位控，在位置控制中提升系统的控制精度和鲁棒性。

2.3.1 力控制

将打磨机器人末端与环境的接触模型等效于弹簧模型，由胡克定律可知：

=(-)

(14)

式中:为环境刚度;为打磨头在工作空间的实际位置;为打磨头在打磨件上的位置。

由于机械臂与环境存在接触，为保持机械臂的稳定工作状态，需对关节角施加一定的关节扭矩，则可将机械臂力控环的动力学方程由式(6)改写为

(15)

式中：为接触力通过雅可比矩阵映射在关节空间上的扭矩。接触力与驱动力矩的关系为

=

(16)

式中:为雅可比矩阵的转置矩阵，具体公式为

=-sin()-sin(+)

=-sin(+)

=cos()+cos(+)

=cos(+)

对力控环采用PID控制方法进行控制，式(16)改写为

(17)

式中:、、分别为PID控制的3个参数；为选择矩阵；为理论输入力。

2.3.2 实际工作空间位置与关节的转换

为方便对打磨机器人进行控制，需将笛卡尔坐标系下机械臂末端运动轨迹转换至关节坐标系下表示。由图1可得关节角位移和与机械臂在实际工作空间中的坐标和之间的关系：

(18)

由式(18)可得：

(19)

根据余弦定理以及的位置关系可得：

(20)

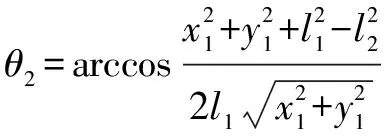
(21)

可得：

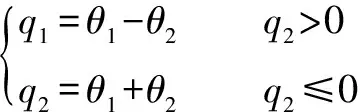
(22)

2.3.3 位置控制

为避免基础振动对位置控制的干扰，在式(6)的基础上引入干扰项，新的动力学方程为

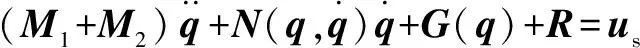
(23)

式中:为干扰项。

令=+,将式(23)变形为

(24)

定义跟踪误差=-，为理论关节角，设计前馈控制率为

(25)

式中:为反馈控制率。将式(25)代入式(24)中得：

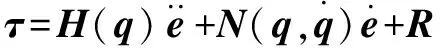
(26)

使用RBF神经网络对扰动进行逼近：

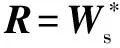
(27)

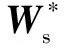
将式(27)代入式(26)中得：

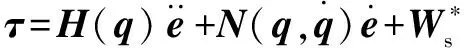
(28)

定义1:

(29)

式中:为常数且大于0。

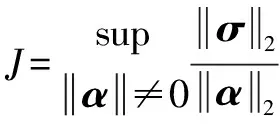
(30)

式中:是的范数，越小，系统的鲁棒性越好。

(31)

将式(28)代入式(29)，得：

(32)

式(32)可化简为式(31)的格式，具体变量如下：

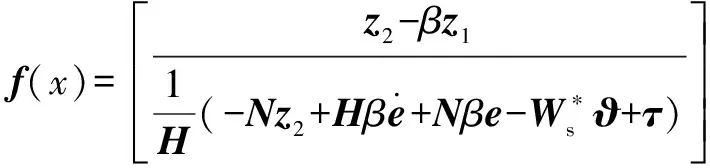
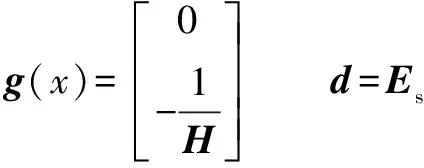
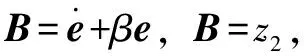
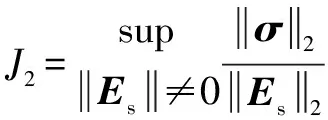
设计慢时变子系统设计自适应调整率为

(33)

式中:为大于0的常数。

设计反馈系统的控制率为

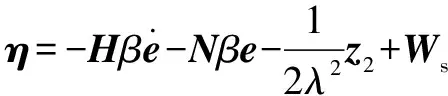
(34)

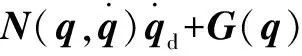
(35)

2.3.4 稳定性证明

对系统的稳定性进行证明，定义Lyapunov函数为

(36)

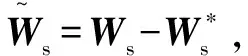
(37)

将式(32)中的第2个公式与式(33)代入式(37)得：

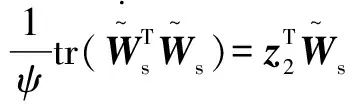
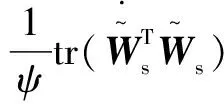
由HJI定理，可定义：

(38)

则有：

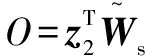
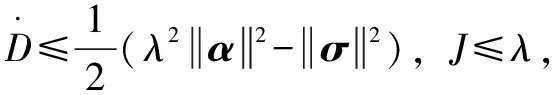
3 仿真与分析

为验证所设计的控制器对存在基础振动时打磨机器人控制的有效性，设计2组数值仿真实验，采用MATLAB/Simulink进行对照分析。第1组：基础振动时，快变控制器打开，慢变控制器中位置控制设置为PD控制，力控制设置为PID控制，检验机械臂末端在工作空间的轨迹跟踪、关节1位置跟踪、关节2位置跟踪以及力的恒定效果；第2组：存在基础振动时，通过关、开快变子系统，设置慢变子系统控制器中位置控制率为神经网络鲁棒控制器，力控为PID控制器，检验系统能否抑制基础振动，实现对期望轨迹和期望力的跟踪响应。施加的基础振动信号如图4所示，系统模型所取的参数和神经网络参数如表1所示。

图4 振动信号

表1 系统模型参数与神经网络参数

图5—图8所示为位置控制为PD控制时，机械臂末端理论轨迹跟踪、关节1(qd1)位置跟踪、关节2(qd2)位置跟踪、期望力的跟踪结果。可知:打磨机器人在作业时，PD控制对振动的振幅和频率有一定的抑制效果，但是其轨迹跟踪出现明显的波动，跟踪效果不理想，与此同时力跟踪出现了明显的超调。

图5 PD控制时机械臂末端位置跟踪 图6 PD控制时关节1位置跟踪

图7 PD控制时关节2位置跟踪 图8 PD控制时力跟踪

图9—图12所示为关闭快时变控制器时机械臂的位置、关节、力跟踪结果。可知：不控制柔性关节振动时，轨迹跟踪及关节1和关节2的位置跟踪明显出现了持续的振动，且打磨力出现明显的超调和振动，但相比于PD控制，神经网络鲁棒控制器对基础振动有着较强的抑制能力，其实际末端轨迹可较好地跟踪理论轨迹。

图9 快变控制器关闭时机械臂末端位置跟踪 图10 快变控制器关闭时关节1位置跟踪

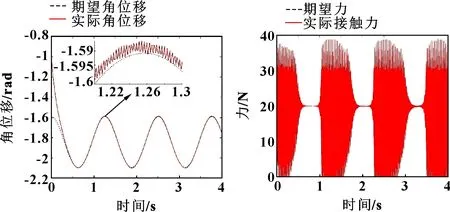
图11 快变控制器关闭时关节2位置跟踪 图12 快变控制器关闭时力跟踪

图13—图16所示为开启快变控制器时机械臂末端的位置、关节、力跟踪结果。可知：机械臂末端轨迹及关节1和关节2有着精确的跟踪效果，相比于关闭快变控制器时轨迹跟踪的效果，快变控制器开启时对柔性关节的振动有很好的抑制作用；其接触力保持在(20±0.1)N内(20 N为理论力)，满足工作要求，保证了加工件的质量。

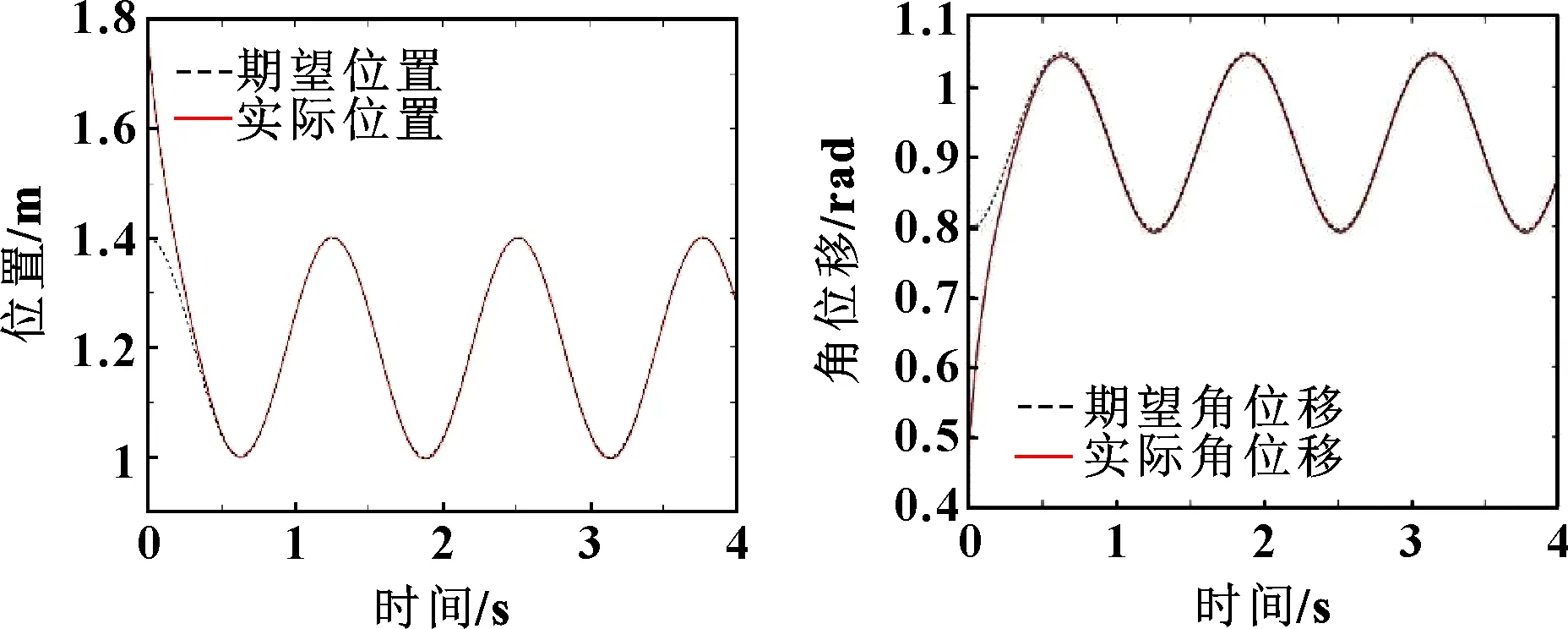
图13 快变控制器打开时机械臂末端位置跟踪 图14 快变控制器打开时关节1位置跟踪

图15 快变控制器打开时关节2位置跟踪 图16 快变控制器打开时力跟踪

4 结束语

对存在外界基础扰动及关节受到力冲击的打磨机器人控制进行了研究，主要结论如下：

(1)在打磨机器人的实际作业中，需保持恒力打磨，但在受到基础振动后，通过传统PD或PID控制难以抑制振动，轨迹跟踪和力跟踪都出现了明显的超调，而通过神经网络鲁棒控制器可以对振动造成的干扰进行抑制，达到工作要求；

(2)在传统刚性打磨机器人的基础上添加柔顺驱动，缓冲了机械臂末端与环境接触时的碰撞力，减少对打磨机器人关节的损伤。但柔顺驱动的引入带来了柔性关节的振动，可以通过奇异摄动法设计控制器对振动进行抑制。结果表明：所设计的控制器能克服打磨机器人在作业时受到的振动影响及抑制柔性关节的振动，实现打磨机器人的轨迹跟踪和恒力打磨。