利用压裂施工停泵压力数据计算裂缝高度

2022-09-14赵立安王志愿修春红贾国龙

非常规油气 2022年5期

关键词：压裂液井筒渗流

赵立安,王志愿,修春红,贾国龙

(中国石油大港油田,天津 300280)

0 引言

水力压裂已成为致密油气及非常规油气开发的核心技术[1]，由于储层、井型及压裂工艺等不相同，地层中的裂缝形态也千差万别[2]，压裂形态的表征成为压裂过程中重要组成部分[3]。

对压裂效果的监测主要有微地震法[4]、电位法[5]及分布式光纤监测[6]，这类裂缝监测方法不仅投入大，而且施工复杂[7]。

对压裂效果评估的另一类方法是对压裂施工数据进行分析，开展压裂效果评价。Nolte[8-11]对压力施工数据进行研究，提出了G函数方法、线性流分析、双对数分析法等。这些分析方法可以得到闭合压力、滤失系数、裂缝半长及地层渗透率等，但分析得出的裂缝半长及渗透率只是一个估算值。Soliman[12]根据脉冲双线性流、线性流和径向流在双对数导数曲线中的斜率分别为1/4，1/2和0进行数据解释分析，这类分析除了获得流体摩阻参数，还可以获得裂缝半长，但裂缝半长需要已知地层渗透率。

采用试井分析方法分析压后停泵压降数据也得到较多应用[13-15]，这类分析都采用试井中的裂缝井试井模型，可以获得裂缝半长及渗透率等。

温杰雄[16]等提出采用滤波方法过滤掉水锤压力波而保留渗流压力，再将井口压力考虑变排量及变密度(加砂)折算到井底压力，由井底渗流压力解释分析得到地层渗透率及裂缝半长。

前人所做工作均为通过压力反演方法得到裂缝半长及渗透率等，但裂缝高度无法得到，这是当前采用压力对压后效果评价最大缺陷。该文在温杰雄等提出的利用压裂施工停泵数据分析基础上，将井筒及裂缝中流体压缩性与达西定律相结合计算裂缝高度，为采用压力施工数据评价压后效果提供新参数。

1 基本理论

1.1 压裂期间的裂缝压力分布公式

压裂是一个十分复杂过程，但从地层压力分布的角度可以将这一过程简化，为此采用如下假设：

1)油藏各向同性且为等厚度；

2)省略压裂过程，假定地层中有一条垂直裂缝；

3)压裂液沿裂缝瞬间注入到地层，之后井筒及裂缝中的压裂液向地层渗流；

4)多孔介质中的流体满足达西流动；

5)地层中的流体及岩石为微可压缩。

根据以上假设，根据李熙喆[17]等的研究可以得到瞬时点源时的压力分布表达式为：

(1)

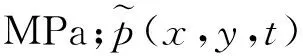
式(1)是地层中点源的压力分布，如果将裂缝看做无限个点源，则沿x轴对点源积分可以得到裂缝井产生的压力分布。图1所示为垂直裂缝井坐标系及点源积分示意图，图2所示为垂直裂缝与井筒位置示意图。对于垂直裂缝井，假设沿裂缝方向为x轴，且注入时刻τ=0，注入量为Vm，这样式(1)中ζ=0,且δν=Vm/(2xfh)。通过对式(1)沿x轴积分，得到垂直裂缝井的压力分布p(x,y,t)。

图1 垂直裂缝井坐标系及点源积分示意图Fig.1 Coordinate system and point source integral diagram of vertical fracture well

图2 垂直裂缝与井筒位置示意图Fig.2 Vertical fracture and wellbore position diagram

式(2)给出了压裂液进入地层后不同时刻的压力分布表达式，利用这一表达式可以计算压裂后地层压力漏斗，图3和图4分别是同一时刻不同裂缝半长时的压力漏斗。从图中可以看出：裂缝附近是一个高压区，远离井筒，压力降低且裂缝半长对压力漏斗影响较大。正是由于压力漏斗的存在，才导致压裂停泵后井底压力随时间减小。

图3 裂缝半长为50 m的压力漏斗Fig.3 Pressure funnel with half length of 50 m

图4 裂缝半长为100 m的压力漏斗Fig.4 Pressure funnel with half length of 100 m

(2)

通过定义无因次参数，可以得到无因次压力，见式(3)：

(3)

地层无量纲压力表达式(3)中，取xD=0,yD=0，可以得到垂直裂缝井瞬时注入时的无量纲井底压力,见式(4)：

(4)

式(4)可以作为压裂停泵期间压降分析的图版，通过对实际停泵压降压力拟合，获得地层渗透率、裂缝半长等。

1.2 裂缝高度的计算

压裂停泵后压力液分布在地层、井筒及裂缝中，由于井筒及裂缝中的压力高于地层中的压力，井筒及裂缝中的压裂液渗流到地层，假设井筒及裂缝空间体积不变，渗流到地层中流体由于压裂液的压缩性使得井底压力降低，根据压裂液压缩系数，定义:

(5)

对方程(5)积分可以得到

V=V0exp[-Cf(p0-p)]

(6)

式中：Cf为压裂液的压缩系数，1/MPa；p0为停泵时刻的压力，MPa；p为停泵t时间的压力，MPa；V0为井筒与裂缝的体积之和，也是压力为p0时的压裂液体积，m3，计算见式(7)。

V0=Vw+2xf·h·w

(7)

式中：Vw为井筒体积，m3；xf为停泵压力解释的裂缝半长，m；h为压裂液漏失的高度，m；w为裂缝宽度，m；V为压力为p时的压裂液体积，m3。

由于停泵后井筒中的流体处于禁止状态，停泵时间t小时，井口压力由p0降为p，其压差(p0-p)与井底压力差相同。压差导致的压裂液体积差(V-V0)就是停泵后裂缝进入地层的压裂液量，可以根据达西定律计算得到。

(8)

式中：VL为停泵时间t小时的压裂液漏失量，m3；k为停泵压力解释的渗透率，μm2；μ为压裂液的黏度，mPa·s。

根据式(6)及式(7),由流体压缩产生的体积差为：

ΔV=(Vw+2xf·h·w){1-exp[-Cf(p0-p)]}

(9)

式(9)和式(8)得到的体积相等，这样就可以得到裂缝漏失高度h的表达式为：

(10)

式(10)中∂p(x,y=w/2,τ)/∂y可通过式(2)得到，对式(2)y方向求偏导数，并在y=w/2处取值，最终可以得到：

(11)

式(10)中的时间t可以取最大的停泵时间Δtmax(停泵时刻为Δt=0)，由于式(10)中每个表达式都有对应的公式，同时部分表达式是特殊函数，并且涉及到时间和x轴的积分运算，可以通过编制计算程序实现对裂缝高度的求解。因此，当通过停泵压降分析得到裂缝半长及渗透率等参数后，由停泵压降曲线中最大时间及对应的最大压降值，就可以计算出裂缝高度。

2 实例分析

这是国内一口致密油压裂井，对井段4 173.0～4 170.0 m和4 115.0～4 113.0 m进行主压裂。最高施工压力为73 MPa，施工排量逐级提升至9.4 m3/min，分别加入3%，3%，5%的粉陶段塞，4%，4%，4%的低密度细陶段塞，连续加砂6%，8%，10%，施工压力69～73 MPa，共加砂40 m3(粉陶2.5 m3、低密度细陶37.5 m3)，压裂层共用液1 800 m3(滑溜水183 m3，基液1 617 m3)，压后停泵压力56.1 MPa，停泵压力梯度为0.028 7 MPa/m。图5所示为该井压裂层的压力施工曲线，对图5中的停泵压降段进行分析，获得渗透率及裂缝半长等参数后，再由式(10)计算裂缝高度。

图6是压裂停泵后前30 s压力随时间变化图，可以看出最高压力约为70 MPa，而最低压力约为45 MPa，压力数据出现震荡，这就是典型的压裂停泵水击所导致[18]，直接使用停泵后的压力数据，由于数据存在剧烈震荡无法获得正确的压力导数曲线。通过滤波技术过滤掉水击压力[19-21]，滤波后的压力本质上就是压裂液通过裂缝进入地层导致压力降落，由于该压力反应的是地层渗流特征，所以可以反演地层渗透率及裂缝半长等。

图6 停泵后前30 s压力图Fig.6 Pressure chart of first 30 seconds after pump-off

图7是该井滤波后停泵压降双对数压力及导数拟合图，可以看出滤波后的压力曲线存在井筒存储段、裂缝线性流段等导数曲线主要特征段，采用2条裂缝模型进行解释反演。通过时间及压力拟合值可以得到SRV区域的渗透率k=4.71×10-3μm2，裂缝半长xf1=63.37 m，xf2=122.6 m，裂缝壁面机械表皮Sm=0.16，说明裂缝壁面由于支撑剂形成部分堵塞。这与图7中压力导数有较高的峰值相匹配。