基于季节-WNN组合模型的煤矿事故预测
2022-09-14郭进平周国悦晏承园
郭进平,周国悦,晏承园
(西安建筑科技大学资源工程学院,陕西 西安 710055)
实现经济增长与保证安全生产是我国国民经济建设面临的两大根本性问题[1]。通过现有安全状况预测未来安全演化趋势,在预测结果的基础上合理有效加强各方面建设,提高本质安全水平,是实现安全生产的有效途径[2-3]。很多学者在安全预测方面已做了大量研究,原始时间序列的安全预测模型方面,一些学者提出了基于偏最小二乘回归法、灰色系统法、马尔可夫链法、贝叶斯法等传统的预测模型及其组合模型[4-8],以挖掘导致事故的高频因素组合及事故突出程度与因素之间的关系。但传统预测模型难以找出系统多元因素与生产事故的非线性交互关系,不能提取对安全预测有利的因素,预测效果不佳。为了提高安全预测精度,有学者提出基于数据分解技术的安全组合预测模型。范忠洲等[9]以全国水上交通事故数据作为样本,建立了灰色BP神经网络组合预测模型,提高了水上交通事故数的预测精度。WU等[10]利用经验模态分解法(EMD)将非平稳原始时间序列分解为高频信号和低频信号,用GM模型预测高频信号序列,用ARMA模型预测低频信号序列,通过叠加各子序列的预测结果,构建了EMD-GM-ARMA模型,为矿山安全生产状况提供高精度、高稳定性的预测。梁文娟等[11]通过建立差分自回归移动平均模型(ARIMA)、最小二乘支持向量机模型(LS-SVM)和BP神经网络模型(BPNN)的组合模型,对某航空公司运输的月度飞行事故进行了预测分析。这类组合预测的方法虽在一定程度上解决了安全时间序列高复杂度的问题,提高了预测精度,但这类方法较多考虑了安全事故发生的离散性和偶然性[12]。事实上,生产领域安全状况受复杂的自然因素和社会因素共同作用影响,存在明显的季节性特征。韩国旭等[13]通过收集陕西省生产安全月度死亡人数数据,发现其具有明显的季节性特征,建立了基于季节性因素的灰色时序模型。袁婧[14]分析施工中存在季节性因素,提出应对特殊情况的应急准备,并展开有效分析,从而为保障工程施工安全和质量提供依据。目前,季节性事故逐渐呈多发趋势,表现出概率高、突发性强、预防难度大的特点,但目前对于这方面的研究并不深入。
本文以我国2015—2020年的煤矿事故死亡人数的月度数据为样本,考虑安全生产过程中的季节效应,通过X-12-ARIMA模型进行季节调整,将事故死亡人数的时间序列分解为平稳时间序列和季节因子序列,季节因子序列每年呈现相同规律,基于小波神经网络(wavelet neural network,WNN)模型对平稳时间序列进行预测。并对比分析当前几种比较典型的预测模型的预测结果,验证季节-WNN组合预测模型的预测精度,以此反映出煤矿生产事故发生的季节性特征,达到良好的预测效果,从而为我国煤矿生产事故的预测提供一种思路。
1 季节-WNN组合模型
1.1 季节调整
季节调整是指对原始月度或季度时间序列中隐含的季节性因素影响进行修正或消除的过程[15],季节调整可以通过X-12-ARIMA模型来实现,采用Eviews软件实现编制程序对时间序列进行季节调整,其过程可分为建模、季节调整和诊断三个阶段[16],如图1所示。

图1 X-12-ARIMA模型结构图Fig.1 Structure drawing of X-12-ARIMA model
1.2 小波神经网络
小波神经网络(WNN)模型的结合方式一般有两种:一种是辅助型结合,另一种是紧密型结合[17-18]。 本文采用紧密型WNN模型,其学习算法为梯度下降法,共有三层,分别为输入层、隐含层和输出层。 拓扑结构如图2所示,其中,X1,X2,…,Xt为WNN模型的输入参数,H1,H2,…,Hj为隐含层传递函数,Y1,Y2,…,Yk为输入值经网络传输后的相应输出值,wij和wjk为网络各层之间的连接权值。

图2 WNN模型结构图Fig.2 Structure diagram of WNN model
1.3 季节-WNN组合模型原理
运用组合预测法[19]将X-12-ARIMA模型与WNN模型进行综合,组建出一种季节-WNN组合模型,其建模步骤如图3所示。

图3 季节-WNN组合预测建模原理Fig.3 Modeling principle of seasonal-WNN combined prediction
1) 将原始数据的时间序列按时间顺序排列成一组随机变量,记为{Xt,t=1,2,…,N},N代表时间的集合。用X-12-ARIMA模型进行分解,得到一个季节调整值序列SA和一个季节因子序列SF,关系式见式(1)和式(2)。
SA=TtIR
(1)
式中:Tt为长期趋势序列;IR为不规则变动因素序列。

(2)
式中:n为时间序列的滑动平均项数;k为季节周期,若k=4,则表示时间序列为季度数据,若k=12,则表示时间序列为月度数据[20]。

3) WNN模型参数权值修正及训练步骤如下所述。
步骤1:设置输入层与隐含层的连接权重值wij,得到隐含层输入参数hj,见式(3)。
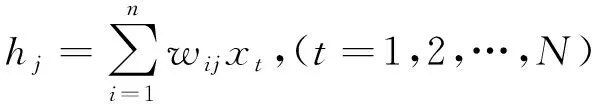
(3)
长期趋势序列Tt与时间t的关系式见式(4)。
Tt=a+bt
(4)
式中:a为平移因子;b为伸缩因子。
由此,调整小波基函数的平移因子a与伸缩因子b,得到隐含层输出参数Hj见式(5)。
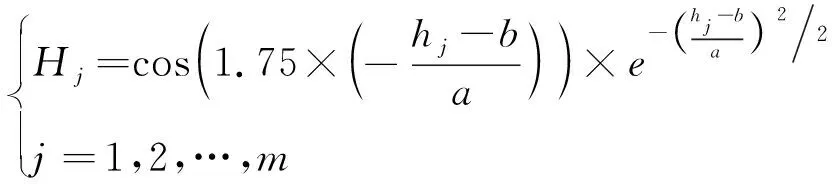
(5)

步骤2:设置隐含层与输出层的连接权重值wjk,得到最终的输出层输出参数Yk表达式见式(6)。

(6)
在控制过程中,实时以WNN模型输出预测值与真实值的差值为依据对WNN模型进行误差分析。通过使预测输出不断接近实际数值,提高预测精度来进行权值修正。 相应的误差函数E见式(7)。

(7)
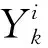
根据得到的误差E来修正网络连接权重值wij、wjk及平移因子a与伸缩因子b。参数修正公式见式(8)~式(11)。
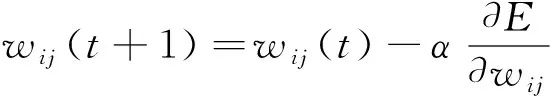
(8)

(9)

(10)
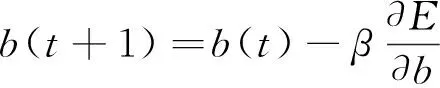
(11)
式中,α和β分别为wij、wjk和a、b的学习速率。
4) 对WNN模型参数权值修正及训练步骤进行判断,误差达到最小时则结束预测,否则返回重新计算,直到达到预测精度为止。

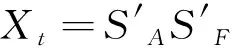
(12)
经过X-12-ARIMA模型进行季节优化调整,再通过WNN预测模型研究,比较各分量的周期变化规律,可以充分揭示出时间序列的结构,掌握其主要的波动特征,以此分析季节因素对安全事故的影响。而且,建立的季节-WNN组合预测模型在研究这种季节因素影响下时间序列的周期波动方面,可有效对数据中的噪声扰动进行排除,具有单一时序方法所无法企及的优势[21]。
2 实例应用
2.1 样本数据来源
本文研究数据来源于国家统计局每年公布的我国煤矿事故死亡人数。由于季节调整模型要求数据必须为月度数据或季度数据,为保证分析结果的准确性和时效性,以2015—2020年每个月的死亡人数作为原始数据样本。将原数据分为两部分:2015年1月—2019年12月的数据用作训练集以构建模型;2020年1月—2020年12月的数据作为测试集来验证模型的预测精度。
表1为2015年1月—2020年12月我国煤矿事故死亡人数的月度数据。由表1可知,事故频发时段多在秋季,死亡人数最多的月份在每年11月;冬季12月份较多,死亡人数最少的月份在每年2月;春季在3月—4月返工时期,事故频发;夏季整体事故数量偏少,月平均死亡人数低于30人,煤矿事故死亡人数整体呈现较为明显的季节性特征。需要注意的是,2020年1月—5月受新冠疫情影响,大多数煤矿企业相继停工停产,煤矿事故每月死亡人数明显低于以往年份。随着疫情得到控制,从2020年6月起煤矿逐渐恢复生产,死亡人数又逐渐增多,继而呈现出与以往相同的季节性特征。

表1 2015—2020年全国煤矿事故死亡人数月度数据Table 1 Monthly coal mine fatalities from 2015 to 2020 单位:人
2.2 季节性校验
根据煤矿事故死亡人数的季节性特征,对其原始数据进行识别,得到全国煤矿事故死亡人数的原始时间序列,如图4所示,其中,横坐标代表时间轴,纵坐标代表死亡人数波动情况。

图4 2015—2020年全国煤矿事故死亡人数原始时间序列图Fig.4 Raw time series chart of coal mine fatalitiesin China from 2015 to 2020
对2015—2020年全国煤矿事故死亡人数时间序列进行自相关分析,结果见图5。由图5可知,显著性水平(Prob)小于0.05,这说明煤矿事故死亡人数时间序列与季节性因素显著相关,即存在明显的季节性特征。
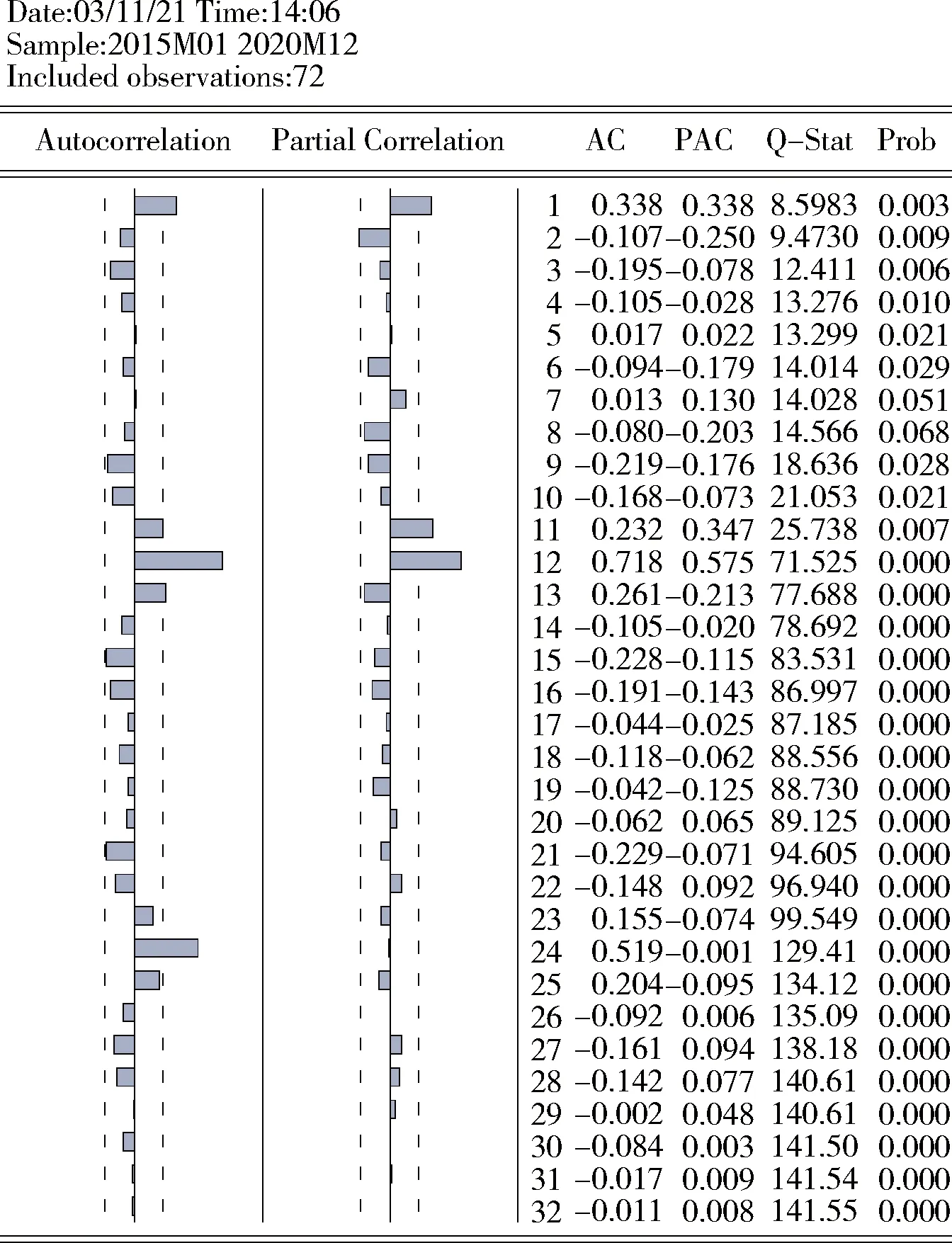
图5 月度死亡人数时间序列自相关检验图Fig.5 Auto-correlation test chart of time seriesof monthly deaths
运用X-12-ARIMA模型对煤矿事故死亡人数时间序列进行季节调整,得到季节调整时间序列图(图6)。由图6(a)可知,季节因子存在周期性变动,每年的第一季度为事故发生最低峰,第四季度为事故发生最高峰。这可能是由于季节变换致使作业环境变化或受春节前后产能调整的影响,员工心理或生理发生微妙变化,容易引起安全事故,导致每年的第四季度事故频发,并以此为时间节点引起季节性周期波动。由图6(b)可知,不规则变动影响因素呈现一种无规律可循的变动,可能包括心理生理影响、气候变化等偶然性因素。由图6(c)可知,剔除季节因素后的时间序列呈现波动特征,此过程时间序列仍处于非平稳状态,还无法进行控制及预测。由图6(d)可知,煤矿事故死亡人数长期波动情况总体呈现非线性降低趋势。
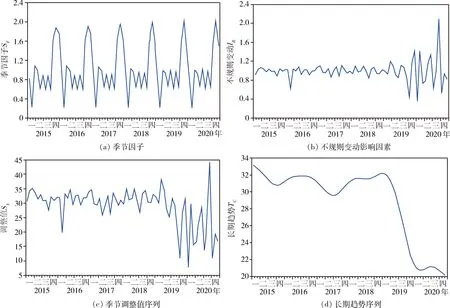
图6 季节调整时间序列图Fig.6 Seasonal adjusted time series diagram
在完成季节调整后,对季节调整值SA进行假设检验。图7为季节调整值SA的假设检验结果,可以看出t-Statistic等于-8.989 022,均小于1%、5%、10%水平下t-Statistic的值,拒绝原假设,认为SA没有单位根,且显著性水平(Prob)小于0.001,说明被调整后的季节调整值时间序列是平稳的。

图7 季节调整值SA检验结果Fig.7 Test results of seasonal adjusted values SA
2.3 季节-WNN组合预测模型可靠性分析
将季节调整值序列小波预测后,按乘法模型与季节因子序列组合得到新的预测时间序列,获取煤矿事故死亡人数的预测结果如图8所示。
由图8可知,单一的WNN模型的预测值与煤矿事故死亡人数真实值相差较大,平均相对误差约为19.62%。 进行季节调整之后,结合WNN模型建立的组合预测模型,通过对2015年1月—2019年12月之间全国煤矿事故死亡人数进行学习训练,发现其训练值与真实值基本一致,均方误差仅为1.86%。对2020年煤矿月度死亡人数进行预测,发现季节-WNN组合模型的预测值与真实值基本吻合,平均相对误差也只有1.11%,说明在考虑安全生产的季节效应后可有效提高安全预测的精度,达到良好的预测效果。

图8 季节-WNN组合预测模型趋势图Fig.8 Trend chart of seasonal-WNN combinedprediction model
2.4 多种预测模型对比分析
选用灰色系统模型、BP神经网络模型等对2019—2020年数据进行预测分析,通过对各个预测模型的误差和稳定性进行分析,分别计算出预测模型相应的平均绝对差值(MAD)、平均相对误差(MAPE)、均方误差(MAE)、均方根误差(RMSE),结果见表2。

表2 各模型预测精度检验结果Table 2 Test results of prediction accuracy of each model
为了更形象直观地突显预测模型的预测效果,图9和图10分别为灰色系统模型和BP神经网络模型与季节调整相结合的构建组合,对其预测结果进行对比分析。
图9为灰色系统模型与季节-灰色系统组合预测模型预测图。其中,煤矿事故死亡人数的真实值呈现波动变化;单一灰色系统模型进行预测的预测值与真实值相差甚远,平均相对误差为46.74%,均方误差高达233.43%,未达到预测效果;季节调整后的灰色系统模型预测值,虽未达到预测目的,但平均相对误差下降29.71%,均方误差下降44.75%,精度有所提升。但相比季节-WNN组合模型,灰色系统模型与季节-灰色系统组合预测模型预测精度较低,不适合对煤矿事故死亡人数进行安全预测。
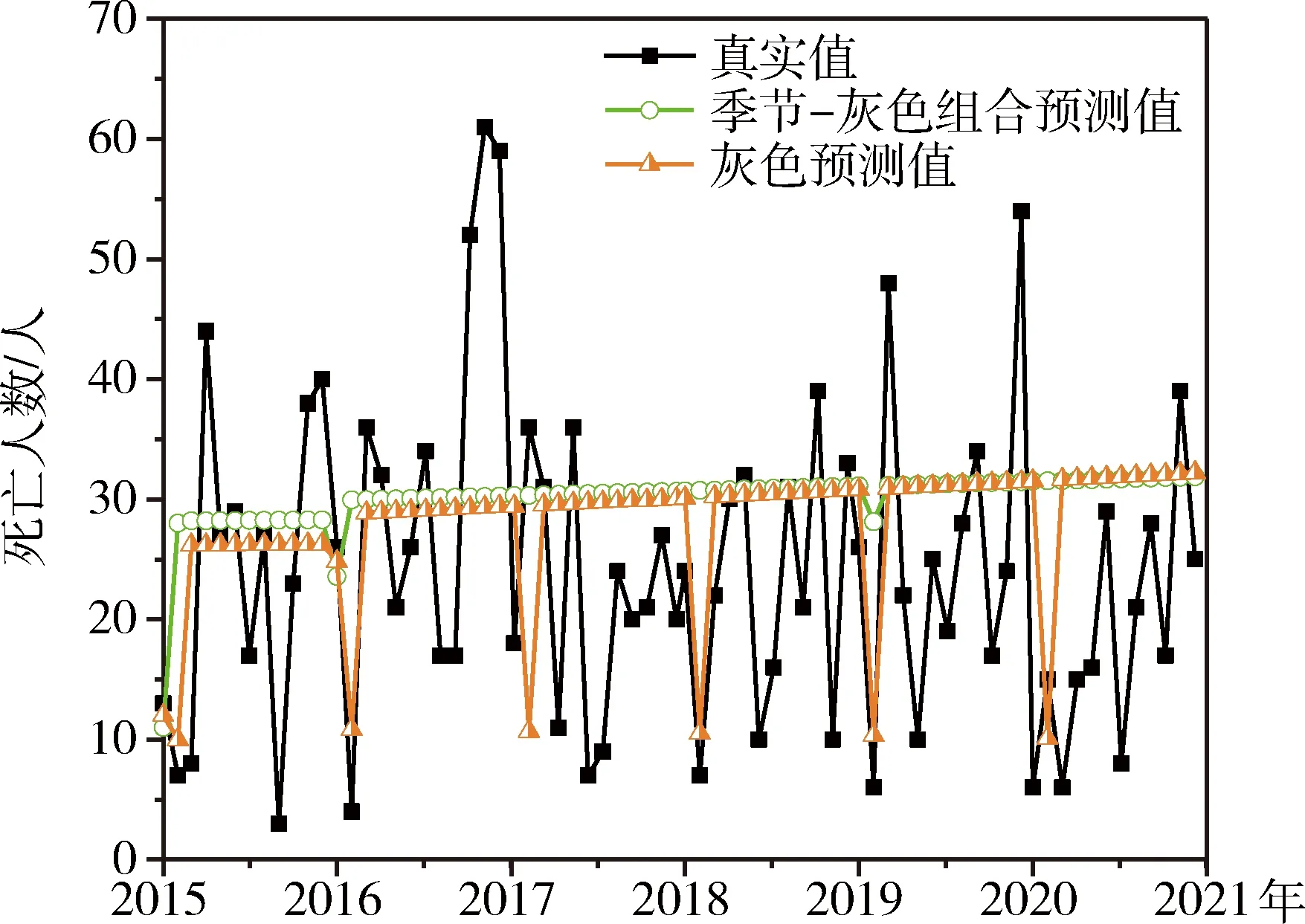
图9 灰色系统模型与季节-灰色系统组合模型预测趋势图Fig.9 Forecast trend chart of grey system model andseasonal-grey system combination model
图10为BP神经网络模型与季节-BP神经网络组合模型预测趋势图。 由图10可知,BP神经网络模型预测值波动幅度较大,平均相对误差为13.19%,
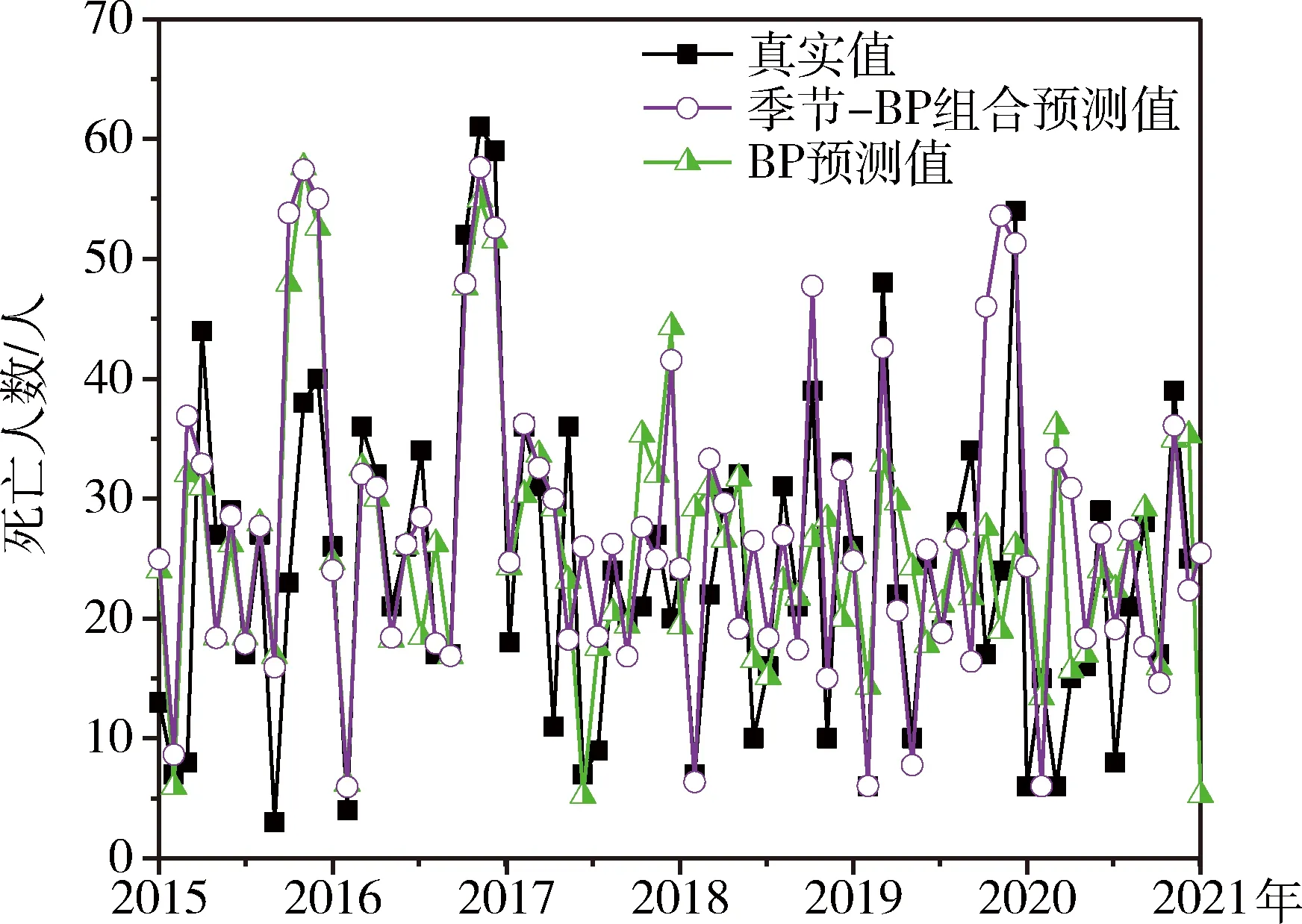
图10 BP神经网络模型与季节-BP神经网络组合模型预测趋势图Fig.10 Prediction trend chart of BP neural network modeland seasonal-BP neural network combination model
均方误差在10%以上,大部分预测值与真实值相差较大,预测效果较差;结合季节调整后的BP神经网络预测模型预测值,平均相对误差降至2.73%,均方误差也只有6.34%,只有小部分预测值与真实值相差较大,预测结果明显较单一,BP神经网络模型预测更为精确。季节-BP神经网络组合预测模型也适合对煤矿事故死亡人数进行安全预测。但相比季节-WNN组合模型,其预测精度仍有待提高。
单一的预测模型由于未排除季节波动的影响,事故死亡人数往往可能存在偶然性,且数据基数较小,因此比季节调整后的预测模型的预测误差更大。而在经过季节调整后,这些单一的预测模型预测精度明显都大幅提升,其中季节-WNN组合模型的整体误差和实际偏差均比其他预测模型的精度更高。季节-WNN组合模型较好地结合了小波变换和时间序列模型的优势,利用X-12-ARIMA模型进行季节调整得到的季节性因素和周期性特征,使得该模型对于时间序列的发展变化趋势刻画较为精确。此外,在季节-WNN组合模型应用过程中还发现,该组合预测模型从小样本数据着手,进行短期预测,使得建模较为简便,短期预测方面表现良好,能够削减因为死亡人数随机性和波动性引起的精度降低等问题,有着很好的应用前景。
3 结 论
1) 通过收集数据分析发现,我国煤矿事故受季节因素的影响较为明显,将安全事故视为按时间次序排列的随机变量序列,而任何时间序列均可通过合理的函数变换后,形成趋势变换和季节周期变换。采用X-12-ARIMA模型对煤矿事故的原始时间序列进行季节调整,运用WNN模型进行函数变换,并将两者相结合进行预测分析,这对于考虑安全生产的季节效应进行安全预测提供了一个新的途径。
2) 本文所建立的季节-WNN组合模型,平均相对误差为1.11%,均方误差为1.86%,说明该组合预测模型预测稳定性较好,预测精度较高,且季节-WNN组合模型从小样本数据着手,建模更为简便,短期预测效果良好,可为煤矿安全决策提供相关理论依据。
3) 通过对我国煤矿事故死亡人数近五年的月度数据组建多模型进行预测分析,运用X-12-ARIMA模型排除季节因素对时间序列的影响,再结合不同预测模型预测的效果好于未经过季节调整的单一预测模型的预测效果。季节-WNN组合模型的预测结果比其他几种预测模型的平均相对误差及均方误差更低,说明其预测精度更高,能较好地反映安全生产过程中受季节因素影响所呈现的规律性变化,有效预测复杂事故系统的发展趋势变化。虽然该组合预测模型短期预测效果显著,但中长期预测精度仍需深入研究。
