含有Kappa 分布电子的多组分等离子体中的 (3+1) 维非线性离子声波

林麦麦 蒋蕾 宋秋影 付颖捷 王明月 文慧珊 于腾萱

(西北师范大学物理与电子工程学院,兰州 730070)

应用约化摄动法推导得到用来描述含有Kappa 分布电子的多组分复杂等离子体中非线性离子声孤波的Zakharov-Kuznetsov (ZK)方程.进而获得了非线性离子声孤波的非线性强度随系统参数的变化规律.同时,利用Sagdeev 势方法求得Sagdeev 势函数,明确了系统参数对含有Kappa 分布电子的多组分复杂等离子体相图、Sagdeev 势函数及非线性离子声孤波的振幅与宽度等传播特征的重要影响.

1 引言

近年来,多组分等离子体的理论研究在物理学各个领域皆有广泛应用,而复杂等离子体中非线性波的研究也是等离子体物理学的热门课题之一[1-6].例如,EI-Taibany 等[7]利用分岔原理研究了孤立波的非线性特性,并首次探讨了双流体复杂等离子体的引力和极化力对尘埃声波结构的影响;Moinuddin等[8]研究了碰撞产生的非线性波和孤立波的冲击特性;Prasad 等[9]首次探讨了电子-离子磁化太阳风等离子体中离子声波解的分岔问题,揭示了离子声波的周期解、超周期解、扭结解、反扭结解、压缩孤立波解和稀疏孤立波解的存在性;Hameed 等[10]研究了非均匀无碰撞、呈Kappa 分布电子且带有尘埃电荷涨落的离子-电子对等离子体中的尘埃声波.与此同时,关于Kappa 电子分布对等离子体非线性波的影响,也受到众多科技工作者的关注[11-13].1992 年,Summers 等[14]在空间等离子体中观测到粒子分布具有非麦克斯韦高能量,可以利用Kappa分布进行建模;Alam 等[15]研究了尘埃声波在含有Kappa 分布电子的复杂等离子体中的斜碰撞效应;Abbasi 等[16]探讨了热黏性流体离子和不同温度的Kappa 分布电子组成的磁旋转等离子体中离子声孤波的非线性特征.

本文研究了含有Kappa 电子分布的多组分复杂等离子体中的(3+1)维非线性离子声波.首先,利用约化摄动法推导得到用来描述(3+1)维非线性离子声波的Zakharov-Kuznetsov (ZK)方程.并通过数值方法讨论Kappa 电子分布及平衡状态下,多种粒子的数密度对ZK 方程非线性系数的影响.然后,利用Sagdeev 势方法得到二维自治系统及Sagdeev 势函数,并借助数值模拟获得系统相图,Sagdeev 势及孤立波的振幅、宽度和波型随Kappa 电子分布和其他系统参数的基本变化规律.

2 基本方程

为了研究含有Kappa 电子分布的多组分复杂等离子体中(3+1)维非线性离子声波的传播特征.假设复杂等离子体由正离子、负离子、离子束和含有Kappa 分布的电子组成,依据大量的空间观测和实验室等离子体检测,在多组分等离子体中由于多种物理过程的出现,导致等离子体中存在着诸如正离子、负离子、离子束和偏离麦克斯韦分布而呈现Kappa 分布的电子,这些粒子对多组分等离子体中非线性波的运动特征存在显著的影响[17].正离子、负离子、离子束遵循麦克斯韦分布[18-21],本文重点分析电子的Kappa 分布对复杂等离子体中离子声波传播的影响.流体力学是离子声波理论研究的方法之一.忽略粒子间的相互碰撞作用,依据磁流体理论,假设多组分的等离子体流体随3 个空间坐标x,y,z和1 个时间坐标t演化,从而给出非线性离子声波的无量纲化演化方程[17]:

其中κ表示Kappa 分布系数.

基于线性化方法和平面波解法,假设

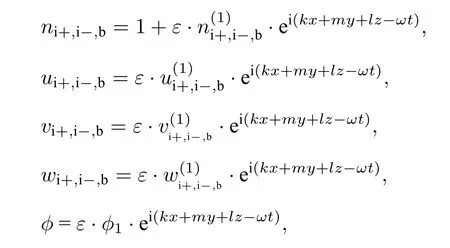
可求得线性波的色散关系为

3 约化摄动法求解ZK 方程

利用约化摄动法研究含有Kappa 电子的多组分复杂等离子体中(3+1)维非线性离子声波的传播特征.首先,对(1)式—(6)式中的自变量进行坐标伸展变换:ξ=ε·x,η=ε·y,τ=ε3·t,ς=ε·(z-v0·t),其中ε为表征非线性强度的小参数,v0为相速度.原始方程组为无量纲化方程组,约化摄动法中引入ε(0＜ε ＜1),可依据无量纲化的具体过程完成多个量的量级确定.由于大于四阶的小量对系统影响较小,为方便计算,将方程中各未知量进行摄动展开:

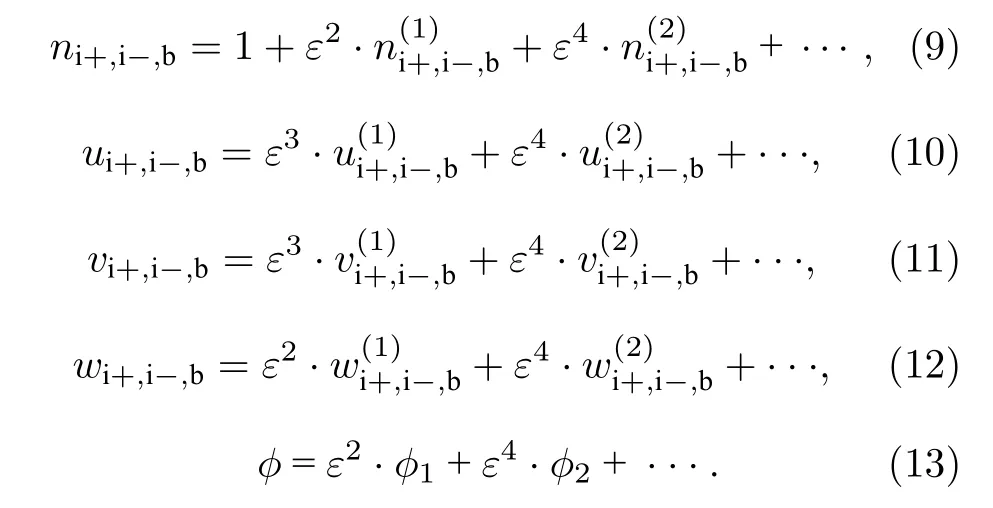
将(9)式—(13)式代入(1)式—(6)式,在ε的最低次幂下有

在ε的较高次幂下,有

在ε的最高次幂下,获得用来描述含有Kappa分布电子的复杂等离子体中(3+1)维非线性离子声波的ZK 方程:

接下来,利用数值方法讨论Kappa 电子分布及平衡状态下多种粒子的数密度对ZK 方程的非线性系数A的影响.图1 给出了系统参数µi+,µi-,µb取不同值时,非线性系数A随电子的Kappa 分布系数κ的变化规律.如图1 所示,A随着κ增大而减小,而其他参数的取值对A的影响则各不相同.从图1(a)和图1(c)可以看出,非线性系数A随着µi+,µb的增大而增大.由可知,当平衡状态下的正离子数密度、离子束密度增多而电子数密度降低时,离子声波的非线性强度A将逐步增强;图1(b)表明非线性系数A随着µi-的增大而减小,考虑到当平衡状态下负离子数密度增大时,非线性系数A将减小.综上所述,图1 表明在含有Kappa 电子的多组分复杂等离子体中,平衡状态下的正、负离子和离子束的数密度和Kappa 电子分布数均对(3+1)维非线性离子声波的非线性系数存在不可忽视的重要影响.

图1 非线性系数A 随Kappa 分布电子数 κ 的变化规律Fig.1.Nonlinear coefficient A with respect to the Kappa distributed electron κ .

4 Sagdeev 势函数及孤立波解

假设ZK 方程有孤立波解ϕ1=ϕ1(θ),θ=lξ+mη+pς -u0τ,其中l,m,p分别为ξ,η,ς三个方向的波数,u0为非线性波的速度,则ZK 方程变形为

(14)式可简化为二维自治系统:

其中,

图2 为二维自治系统(15)式的相图随着Kappa电子分布系数κ的变化图,其中其他系统参数取值分别为α=1,β=0.7,p=m=l=0.4,u0=0.2 .由于p,l,m对孤波振幅均有影响,所以取适当值使得振幅处于恰当范围更有益于数据分析,模拟实验中可以得到p=m=l=0.4 时图形最优[17-20].由图2(a)可以看出,在含有Kappa 电子分布的多组分复杂等离子体系统中同时存在线性波解、非线性波解和孤立波解3 类轨道.通过对图2(a)—(c)进行比对,系统相图表明当系统参数取值不同时,线性波解和非线性波解会出现在含有Kappa分布电子的多组分等离子体系统中波动过程的两个不同时间段,并表现出线性波、非线性波和孤立波3 种不同的波动行为特征.复杂等离子体系统中所含的Kappa 电子分布数的改变,只会影响系统相图中不同类型离子声波解的存在范围,而不会改变系统相图中不同类型离子声波解存在的基本属性.

图3—图5 描绘了系统相图随系统参数µi+,µi-和µb的基本变化,其结论与图2 基本类似.考虑到,这意味着对于含有Kappa 电子分布的多组分复杂等离子体而言,系统平衡状态时的正、负离子和离子束数密度,以及电子数密度的不同,只会使系统相图中不同类型离子声波解的存在范围发生改变,而不会导致系统相图中离子声波的线性波解、非线性波解和孤立波解这3 种不同类型的波解结构发生改变.

图2 系统相图随Kappa 电子分布数 κ 的变化Fig.2.The variations of system phase diagram with Kappa electron distribution number κ .

图3 系统相图随 µ i+ 的变化Fig.3.The variations of system phase diagram with µ i+ .

图4 系统相图随 µ i- 的变化Fig.4.The variations of system phase diagram with µ i- .

图5 系统相图随 µb 的变化Fig.5.The variations of system phase diagram with µb .

其中,Sagdeev 势函数形式为

图6 给出了Sagdeev 势函数随不同参数的变化规律.图6(a)—图6(d)中Sagdeev 势曲线与横轴均存在交点ϕm,且ϕm＞0,这表明该系统仅存在压缩型孤立波.表1 为 Sagdeev 势V(ϕ)=0,µi+,µi-,µb,κ取不同值时,对应振幅的大小.

表1 Sagdeev 势 V (ϕ)=0,µ i+,µ i-,µ b,κ 取不同值时,对应振幅的大小Table 1. Amplitude of solitary waves with respect to µ i+,µ i-,µ b,κ at Sagdeev potential V (ϕ)=0 .

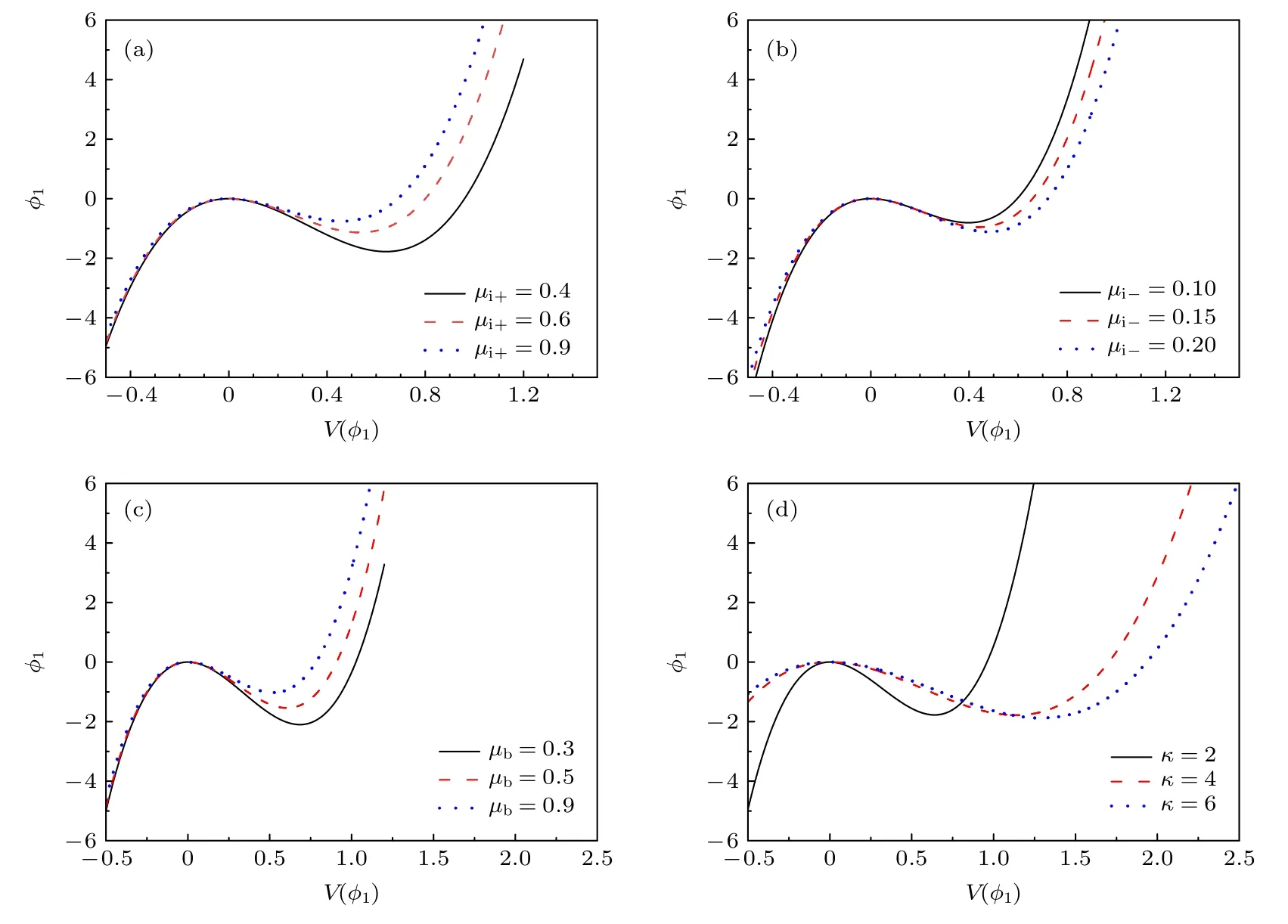
图6 Sagdeev 势函数 V (ϕ1) 的变化规律Fig.6.The variations of Sagdeev potential function V (ϕ1) .

孤波振幅随着µi+,µb的增大及µi-,κ的减小而减小.根据数据分析可知,随着µi+的增大振幅减小幅度越来越小,随着µi-增大,振幅变大的幅度比较均匀,随着µb的增加,振幅减小的幅度较为均匀,而随着κ的增加,振幅减小的幅度越来越小.由于多组分复杂等离子体系统中.这说明: 当多组分复杂等离子体系统中所含的Kappa 电子分布数、负离子数密度的增大时,系统中的压缩型孤立波的振幅将减小;随着正离子数密度、离子束数密度的增大振幅减小,随着κ的增加,振幅减小的幅度越来越大.另外,若平衡状态下的正离子和离子束数密度降低,而负离子束密度和Kappa 电子分布数增加,则导致孤立波的振幅增大,与此同时,孤立波振幅的改变与正离子、负离子和离子束数密度的改变紧密相关.以上结论表明: 复杂等离子体系统中的多种因素均对Sagdeev势函数及孤立波的波形特征存在重要影响.

对Sagdeev 势方程(16)式进行求解,可得到的孤立波解形式为

其中

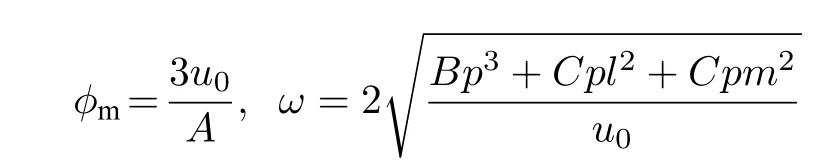
分别为孤立波的振幅与宽度.

图7 孤波振幅 ϕ m 随Kappa 分布电子数 κ 的变化规律Fig.7.The amplitude of solitary waves ϕ m with respect to the Kappa distributed electron number κ .

图9 给出了孤立波的波形随系统参数的变化趋势,其他参数取值分别为p=l=m=0.4,u0=0.5 .图9 显示当系统参数µi+,µi-,µb和κ取值各不相同时,该系统中仅存在振幅大于0 的压缩型孤立波.该结论与Sagdeev 势函数的分析结果一致.由图9(a),(c)可以看出,当系统参数µi+和µb增加时,孤立波振幅减小且宽度增大;而µi-和 Kappa电子分布数κ增加时,孤立波振幅增大且宽度减小.以上结果与图6—图8 中的结论一致.综上所述,含有Kappa 电子分布的多组分复杂等离子体系统中仅存在压缩型孤立波,且系统中正、负离子和离子束的数密度以及电子Kappa 分布情况均对非线性离子声孤波的振幅,宽度及波形存在不可忽略的重要影响.

图8 孤波宽度 ω 随系统参数 µb 的变化规律Fig.8.The variations of the solitary wave’s width ω with respect to the parameter µb .

图9 孤立波 ϕ 1 的波形变化规律Fig.9.Waveform variation law of the solitary waves ϕ 1 .

5 结论

本文研究了含有Kappa 电子分布的多组分复杂等离子体中离子声孤波.利用约化摄动法求得用来描述非线性离子声波的ZK 方程,通过分析与讨论从理论上研究了不同参数对非线性系数的影响.结果表明,非线性强度随着正离子、离子束数密度的增大而增大,随负离子数密度和Kappa 电子分布数κ增大而减小;平衡状态时,孤立波振幅随着正离子、离子束数密度的增大而减小,随负离子数密度和Kappa 电子分布数κ增大而增大;孤立波宽度随正离子、离子束数密度的增大而增大,随负离子数密度和Kappa 电子分布数κ增大而减小.与此同时,还利用Sagdeev 势方法求解得到二维自治系统和Sagdeev 势函数,通过数值模拟给出的相图显示: 多组分复杂等离子体系统中存在非线性波解、线性波解和孤立波解,且孤立波具有振幅大于0的压缩型特征,与此对应的Sagdeev 势函数的变化规律与相图结果一致.通过进一步深入讨论,不难发现: 多组分复杂等离子体系统中的多种系统参数,包括平衡状态下的正、负离子和离子束数密度以及Kappa 电子分布数等,均对非线性离子声孤波的振幅、宽度和波形存在不可忽视的重要影响.本文利用约化摄动法所获得的非线性离子声孤波的演化特征随Kappa 分布系数的变化规律,与其他方法所得的非线性系数孤立波随Kappa 分布系数的变化规律保持一致[22].