基于SO 分子振转能级计算其宏观气体摩尔热容*

文琳 樊群超† 蹇君 范志祥‡ 李会东 付佳 马杰 谢锋

1) (西华大学理学院,高性能科学计算省高校重点实验室,成都 610039)

2) (山西大学物理电子工程学院,量子光学与光量子器件国家重点实验室,太原 030006)

3) (清华大学核能与新能源技术研究所,先进核能技术协同创新中心,先进反应堆工程与安全教育部重点实验室,北京 100804)

本文在研究SO 宏观气体摩尔热容的工作中,进一步考虑了分子内部的转动贡献,通过联立能获得分子某电子态完全振动能级的变分代数法 (variational algebraic method,VAM) 和RKR (Rydberg-Klein-Rees) 方法构建了SO 电子基态的势能函数,解析求解获得了该体系的振转能级,进而采用量子统计系综理论计算得到了300—6000 K 温度范围内SO 宏观气体的摩尔热容.将本文的计算结果与其他几种理论模型的计算结果进行比较分析,结果表明: 当采用基于全程势能曲线求解的完全振转能级来计算热力学性质时,得到的摩尔热容与实验结果更为吻合.本文利用分子完全振转能级计算摩尔热容的思路,弥补了前一阶段工作中仅采用近似模型表征分子转动行为来计算热容的不足,为基于微观统计过程求解宏观热力学量提供了新的研究范式.

1 引言

在涉及化学反应的许多应用中,物质的热力学性质尤为重要[1].摩尔热容是系统最基本的热力学量之一,实验中常常测定的就是热容值,掌握系统的热容对明确物质的宏观演化过程和规律具有重要意义[2].

在研究由许多粒子以及一些物质组成的宏观系统时,可以借助统计物理学通过对特定数量粒子的动态量进行统计平均来预测系统的热力学性质[3],即通过分子微观性质构造配分函数进而得到系统的宏观热力学性质.因此,配分函数的构建与精确计算对系统宏观热力学量的研究至关重要,而近年来人们对配分函数的研究也取得了丰硕成果.早在1988 年,Irwin[4]就得到了基于最小二乘法的配分函数多项式,计算获得了冷恒星大气状态方程的解,但对高温部分的配分函数却难以有效预测;2003 年,Fischer 等[5]使用插值法计算了70—3000 K 温度范围内HITRAN 数据库中所有分子总的内部配分函数,为气体宏观热力学性质的研究提供了宝贵的参考数据;2009 年,伍冬兰等[6]采用麦克劳林和谐振子近似,通过乘积近似模型构造了20—6000 K温度范围内SiO2分子总的配分函数.2016 年,贾春生课题组[7]基于改进的Manning-Rosen 势能函数计算得到了双原子分子的振动配分函数,并进一步计算了7Li2分子电子态的振动平均能、振动比热、振动自由能和振动熵等热力学性质;同年,Maltsev 等[8]发展了使用Morse 势和远距离静电吸引势来计算分子内部配分函数的模型,并以此模型计算获得了ArH 和ArH+分子的宏观热容、熵、焓等热力学量[9];2017 年,Ikot 等[10]使用非相对论量子力学框架下的渐近迭代法计算得到了K2分子电子基态的振动能谱,进而构建了体系的振动配分函数,最后计算获得了该分子的振动内能、振动自由能、振动熵和振动热容.同年,王小霞等[11]采用第一性原理方法,通过配分函数研究了H2的振动态,并且计算了其吸附态的熵;2019 年,Maltsev 等[12]利用原子间相互作用势模型,计算了298.15—10000 K温度范围内和Ar2分子的配分函数,并进一步得到了系统的热力学函数.2020 年,Horchani 和Jelassi[13]利用改进的Rosen-Morse 势分析了量子修正对Cs2分子振动配分函数的影响,并与经典配分函数进行了比较,计算得到了系统的振动平均能、振动比热、振动自由能、振动熵等相关热力学性质.2021 年,Ziga 等[14]对Pachucki 和Komasa 确定的从头算绝热势能函数的束缚能级进行变分处理,获得了分子氢同位素准束缚的振转能级,进而计算了体系的配分函数,最后获得了系统的自由能、热容、熵等热力学量.

上述研究为人们获得精确的配分函数,以求解系统的宏观热力学性质做出了重要贡献,给出了一条利用分子的微观振转信息建立配分函数,进而预测体系宏观热力学量的有效途径.却仍然存在以下两个问题有待完善: 一是随着温度升高,分子内部运动更为复杂,难以准确预测高温状态下的配分函数和热容;二是由于实验条件的限制,难以获得较为完整的转动能级信息,这给准确求解分子转动行为对其宏观气体热力学性质的影响带来了一定困难.

在前期的研究工作中,课题组基于变分代数法(variational algebraic method,VAM)[15]得到的完全振动能级,构造了SO 分子基态的振动配分函数,并由此获得了仅与该分子微观振动效应相关的宏观热力学量[16].随后,为了进一步考虑分子转动行为对热力学量的影响,课题组将麦克劳林近似模型[17]作为转动贡献构建了转动配分函数,通过乘积近似构造了NO 分子总的内部配分函数,从而计算获得了体系的宏观热力学性质[18].实际上,以上这种转动效应的近似处理给计算结果带来了不小的误差,为了解决这个问题,本文在前期研究工作的基础上,利用VAM 与RKR (Rydberg-Klein-Rees)[19-21]方法,首先构建了体系包含高激发态振转行为在内的全程势能曲线,然后求解一维薛定谔方程获得其完全振转能级,从而建立体系总的配分函数,最后借助量子统计系综理论[22]计算得到了系统的宏观摩尔热容.

2 理论与方法

利用分子精确的微观能级结构有效构造体系的配分函数,从而借助量子统计系综理论获得分子的宏观热力学量,是人们从理论上正确预测体系热力学性质的重要方法之一.对于给定的某双原子分子电子态,可利用VAM 方法获得其完全振动能级和振动光谱常数,振动能级的表达形式为[15]

对于某分子电子态,实验上往往能够测得精确的低激发态振动能级.因此,在实验测得的n个振动能级中选取m个能级代入(2)式,可以得到N=组振动光谱常数,再利用相应的物理判据[15]可选择一组最优的光谱常数和完全振动能级.

基于以上VAM 方法获得的完全振动能级和振动光谱常数,借助RKR[19-21]方法和部分实验转动光谱常数,构建体系精确的势能曲线,再通过求解如下体现了势能曲线与振转能级之间定量关系的薛定谔方程[23]得到体系的完全振转能级[24]:

式中,gi表示能级简并度;εi为第i个能级;ε0为最低能级;玻尔兹曼常数kB=1.380651 × 10—23J/K.若不考虑核自旋相互作用,分子的能量可用电子能量、振动能量和转动能量三部分来进行表示[27-29].此时,分子内部配分函数还可以表示为

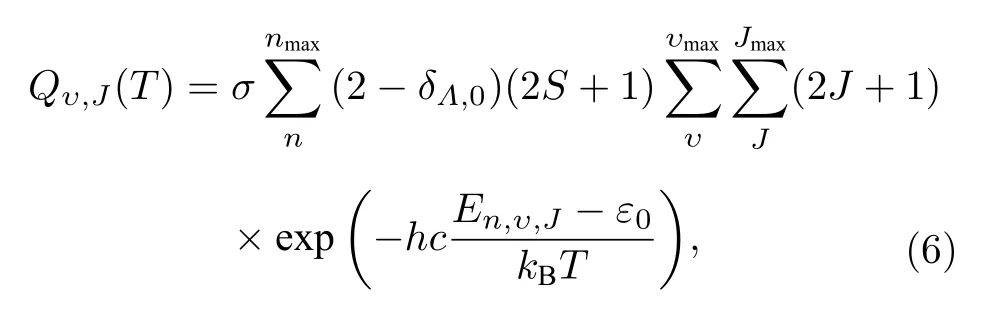
式中,σ是对称因子 (同核分子取σ=1/2,异核分子为σ=1 ); (2-δΛ,0)(2S+1) 表示电子简并度,Λ是电子轨道角动量投影到核间轴上的量子数;S是电子自旋角动量量子数; (2J+1) 表示转动简并度;c表示光速;En,υ,J为量子态 (n,υ,J) 的能量,假定分子均处于基态,那么Eυ,J即为基态分子的能量.

除分子内部运动外,分子平动也会对其宏观热力学量产生影响.当给定分子占据的空间体积V时,还可以给出其平动配分函数为[30]

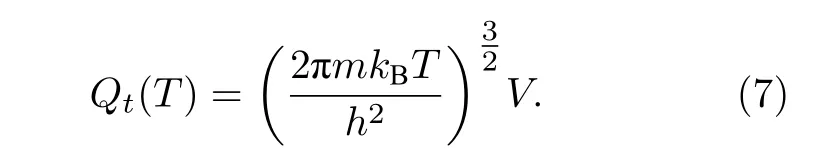
联立(6)式和(7)式,以及理想气体状态方程PV=n′RT(其中n′为摩尔数),可以得到体系总的配分函数:

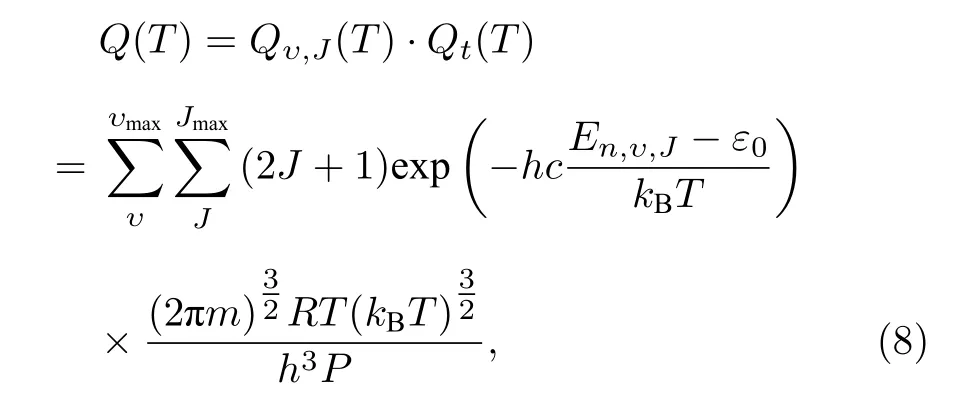
P为压强;普适气体常数R=8.31441 J/(mol·K).

利用构造的配分函数,通过量子统计系综理论即可求得体系的摩尔热容Cm:

其中NA(=6.022252 × 1023/mol) 是阿伏伽德罗常数.

上述方法通过构建精确的双原子分子势能曲线,求解一维薛定谔方程,使用得到的振转能级对体系的配分函数进行计算,再结合量子统计系综理论,对其宏观热力学量进行求解.其关键在于,通过构建精确的势能曲线求解获得了实验上难以测量的双原子分子完全振转能级,使得可以直接计算分子的振转行为对其宏观热力学量的贡献.相对于前期工作中采用近似模型表征转动行为的计算方式,物理模型得到了更合理的优化,同时进一步提高了计算结果的精确度.

3 应用与讨论

SO 是人们熟知的双原子分子,为大气主要污染物之一,是一种短寿命的自由基中间体[31],同时也是重要的星际分子之一[31-33].获得大气气体独特的热力学性质是高温混合气体[29]热力学模型的重要理论支撑,可用于探索星际气体组成的关键信息.本文从SO 分子电子基态的实验振动能级和转动光谱常数出发,采用一系列理论计算方法,研究了SO 宏观气体的摩尔热容.

首先,根据SO 分子X3Σ-(电子基态) 的26 个实验振动能级[34],使用VAM 方法计算了该体系的振动光谱常数和完全振动能级,光谱常数列于表1中.表1 还列出了完全活性空间自洽场 (complete active space self-consistent field,CASSCF);单、双组态相互作用 (singles and doubles configuration interaction,CI-SD);四阶Møller-Plesset 微扰理论的单、双、四元替换 (the fourth order Møller-Plesset perturbation theory with single,double,and quadruple substitutions,MP4SDQ)[35]等三组不同方法和实验测量得到的振动光谱常数.由表1 可知,实验及其他理论方法仅能获得两个振动光谱常数,且理论值与实验值相差较大.VAM 方法所得光谱常数比其他几种理论方法的结果更为接近实验值.

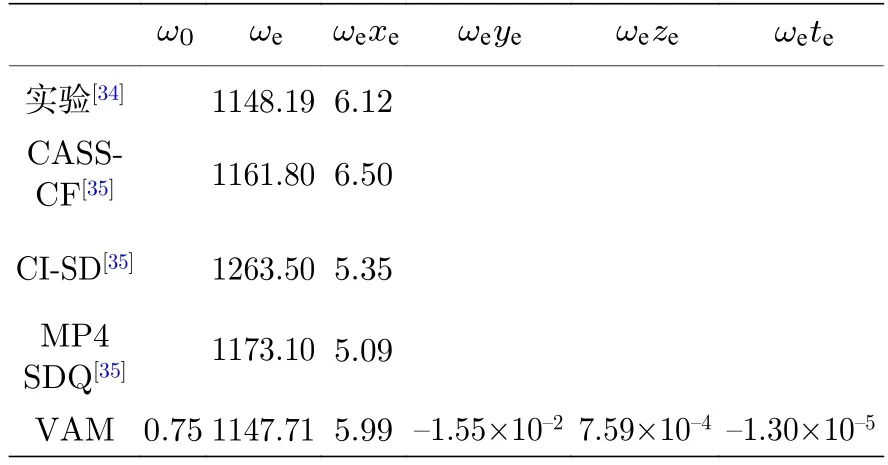
表1 不同方法所得SO 分子电子基态的振动光谱常数(单位: cm—1)Table 1. Vibrational spectral constants of SO in the ground electronic state obtained by different methods (in cm—1).

然后结合VAM 振动光谱常数和利用Bυ实验值[36]拟合得到的7 个转动光谱常数,通过RKR 方法得到了SO 分子电子基态的势能曲线数据.图1为本文获得的势能曲线和实验RKR 势能曲线[34]的对比图.由图1 可以看出,基于VAM 和RKR 方法构建的势能曲线不仅在短程区域与实验RKR吻合得很好,还计算得到了SO 分子长程区域的势能数据,离解区域也很好地趋近实验离解能=43792.00cm—1[34].

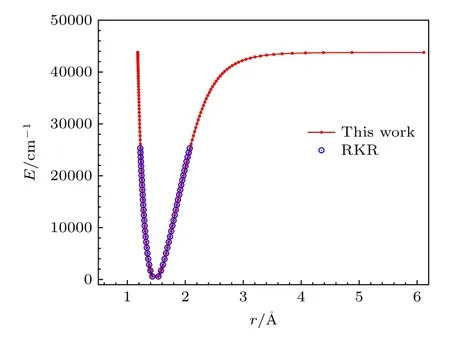
图1 基 于VAM 和RKR 方法构 建的势 能曲线 与实验 势能曲线的对比Fig.1.Comparisons of the potential energy curves constructed based on the VAM and RKR method with those experimentally.

通过LEVEL 程序利用获得的势能曲线求解一维薛定谔方程,得到了SO 分子电子基态的完全振转能级,构造获得了体系总的配分函数.随后,借助量子统计系综理论,使用不同构造形式的配分函数分别计算了300—6000 K 温度范围内SO 气体的摩尔热容: 利用乘积近似模型计算得到的热容[18](前者以实验振动能级作为振动贡献,后者以VAM 完全振动能级作为振动贡献;转动部分均采用麦克劳林近似公式[17]);基于实验振转能级计算获得的热容;本文基于完全振转能级计算得到的热容,由表示.

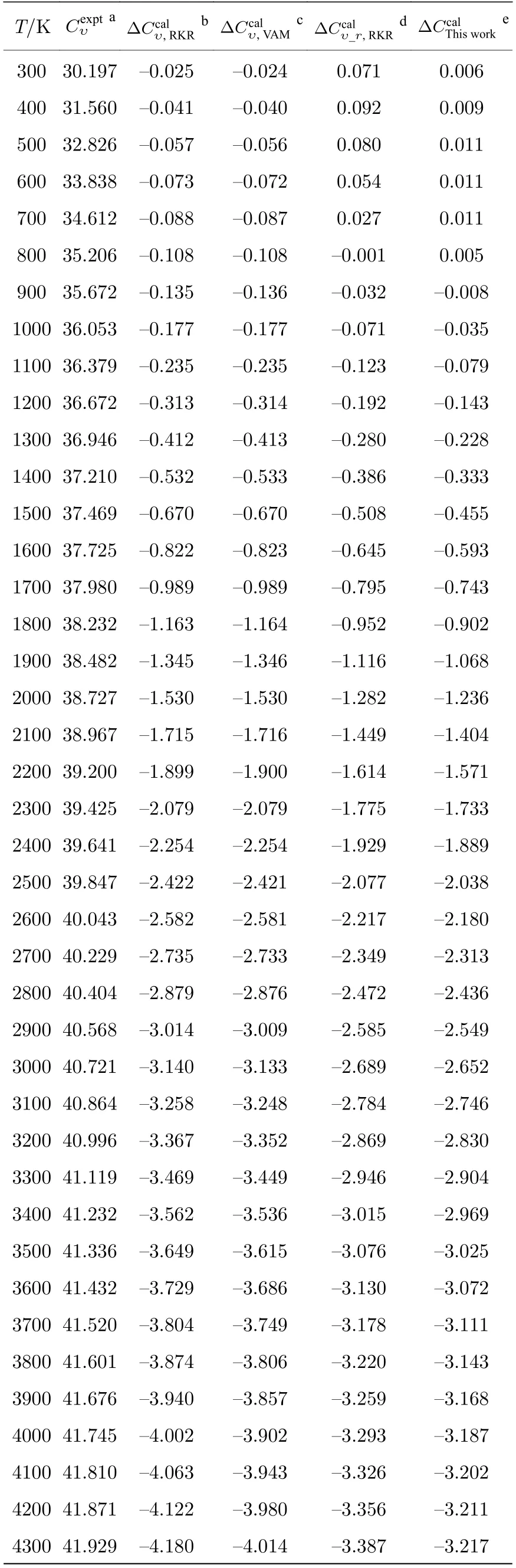
表2 不同摩 尔热容 与实验 值的误 差 (单 位:J·mol—1·K—1)Table 2. Errors between different molar heat capacities and observed experimentally (in J·mol—1·K—1).

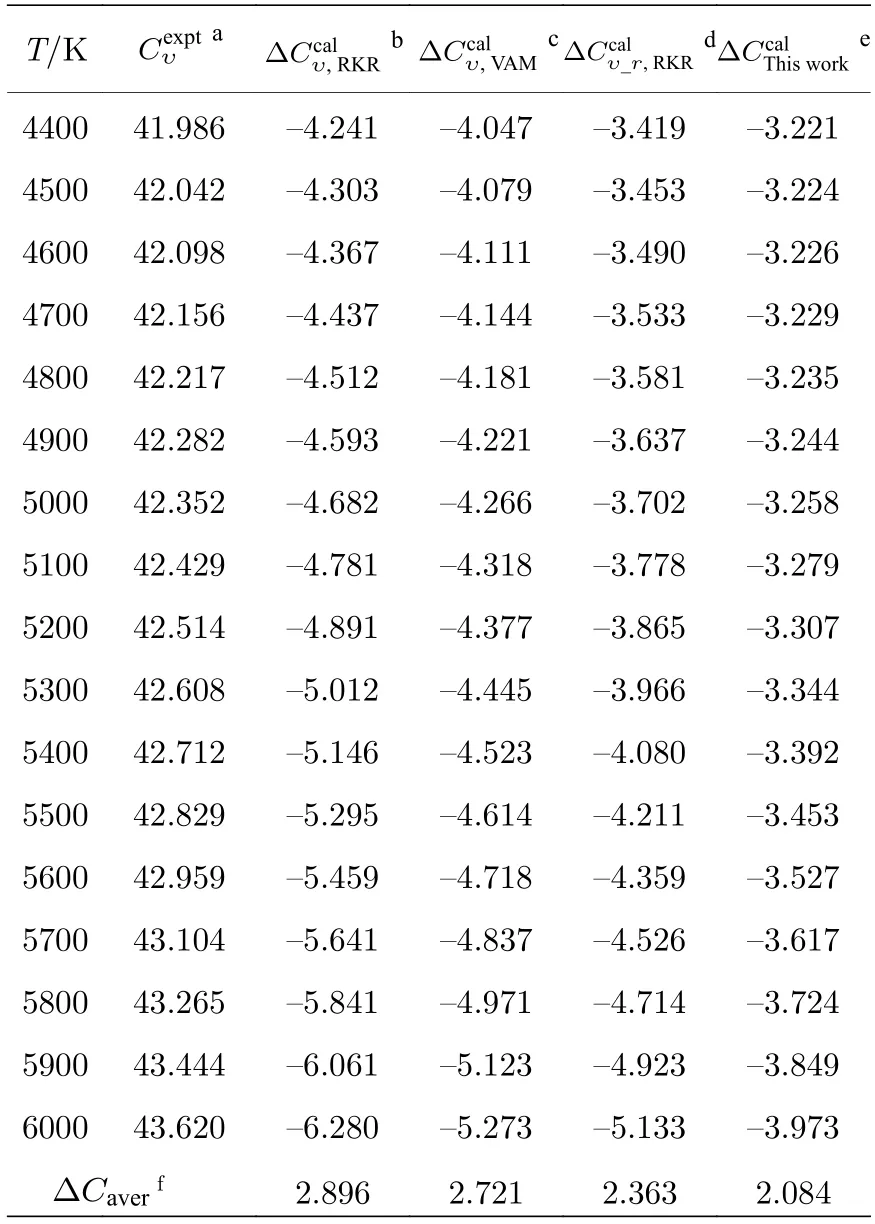
表2 （续）不同摩尔热容与实验值的误差 (单位:J·mol—1·K—1)Table 2 (continued).Errors between different molar heat capacities and observed experimentally (in J·mol—1·K—1)

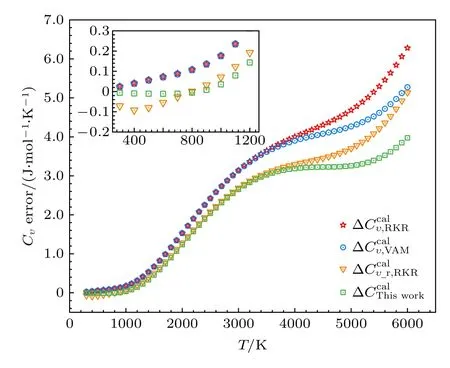
图2 不同摩尔热容误差的比较Fig.2.Comparisons of the errors of different molar heat capacities.

4 结论

本文基于课题组前期有关双原子分子配分函数的研究,对转动部分贡献进行了改进,计算获得了SO 分子宏观气体的摩尔热容.采用课题组建立的VAM 方法,借助实验上测得的26 个精确的振动能级计算得到了可以表征完全振动能级的振动光谱常数.再结合实验Bυ值拟合得到的7 个转动光谱常数反演获得了包含分子高激发态振转行为的全程势能曲线,对其求解薛定谔方程得到了体系的完全振转能级,最后通过量子统计系综理论计算了SO 气体的宏观摩尔热容.与其他理论模型所得结果作比较发现,通过振转能级直接计算热容比采用乘积近似模型获得的结果更为接近实验值,且采用完全振转能级比采用实验获得的有限振转能级获得了更优的结果.本文的方法既包含了完整的微观行为信息,又考虑了振转耦合效应,计算结果较前期方法所得结果更接近实验值,能较好还原双原子分子气体的宏观摩尔热容.