As/HfS2 范德瓦耳斯异质结电子光学特性及量子调控效应*

张仑 陈红丽 义钰 张振华

(长沙理工大学,柔性电子材料基因工程湖南省重点实验室,长沙 410114)

两种或两种以上的单层材料堆垛成范德瓦耳斯异质结是实现理想电子及光电子器件的有效策略.本文选用As 单层及HfS2 单层,采用6 种堆垛方式构建As/HfS2 异质结,并选取最稳结构,利用杂化泛函HSE06 系统地研究了其电子和光学性质以及量子调控效应.计算发现,As/HfS2 本征异质结为Ⅱ型能带对齐半导体,且相对两单层带隙(＞2.0 eV)能明显减小(约0.84 eV),特别是价带偏移(VBO)和导带偏移(CBO)可分别高达1.48 eV 和1.31 eV,非常有利于研发高性能光电器件和太阳能电池.垂直应变能有效调节异质结的能带结构,拉伸时带隙增大,并出现间接带隙到直接带隙的转变现象,而压缩时,带隙迅速减少直到金属相发生.外加电场可以灵活地调控异质结的带隙及能带对齐方式,使异质结实现Ⅰ型、Ⅱ型和Ⅲ型之间的转变.此外,As/HfS2异质结在可见光区域有较强的光吸收能力,且可通过外加电场和垂直应变获得进一步提高.这些结果表明As/HfS2 异质结构在电子器件、光电子器件和光伏电池领域具有潜在的应用前景.

1 引言

近年来,新兴二维材料由于其优异的物理性质[1-4]引发了人们的研究热潮,石墨烯[5]、h-BN 单层[6]、硅烯[7]、磷烯[8]、过渡金属硫化物(TMDs)[9]等相继被制备成功.然而,这些二维材料也存在某些缺陷,如石墨烯和硅烯虽具有很高的迁移率(约104cm²/(V·s)),但它们是零带隙半金属(semi-metal)[3,10],相关晶体管的开关比很低;而h-BN 单层带隙过大,限制了其作为电子器件的实际应用;典型过渡金属硫化物MoS2,虽然具有中等大小的直接带隙(约有1.8 eV)[10],且相关晶体管的开关比很高,但其载流子迁移率不高[11],电流承载能力较弱;磷烯载流子迁移率较高,但暴露在空气中很容易被氧化.所以,为了突破单一材料的这些局限性,由两种及以上二维材料构建成的范德瓦耳斯异质结被广泛研究[12,13],它不仅能保留各单层材料的优良性质,也能获得优于单层材料的电子结构和光学性质,预期在光电器件[4,14]、电池领域[15]和光催化[16-18]等方面有着光明的应用前景.例如,基于MXene/GaN范德瓦耳斯异质结的紫外(UV)光电二极管[19]在弱紫外光下的峰值量子效率可提高到 99%以上,且在355 nm 紫外光照射下的功率转换效率高达7.33%.MnS/MoS2范德瓦耳斯异质结内置电场能增强Li+/Na+插层动力学,以提高电荷输运能力[20].而Cu2WS4/NiTiO3异质结[21]在可见光波长范围内具有很高的量子效率(AQE).目前,实验上可以通过多种方法制备异质结,如 PET stamp 法[22,23]、化学气相沉积法[24]等.

最近制备成功的砷烯(As 烯,As 单层)[25-26],具有α相和β相结构,其中β相单层是六边形蜂窝状结构,能稳定存在于空气中,易于制备.研究发现,它是间接带隙半导体,带隙约为2.2 eV,在室温下,As 单层具有高载流子迁移率特性(约103cm²/(V·s)),其相关晶体管的开/关比可达约104[25].它的光吸收范围从可见光覆盖到紫外光区域,然而对可见光的吸收较弱[26],可以通过设计缺陷[27-29]、掺杂[30,31]、表面功能化[32]和构建异质结[32]等方法调节它的电子结构.As 烯与InSe 组成的异质结[32]在2%的垂直应变下,能获得更高的载流子迁移率.HfS2是典型的过渡金属硫族化合物,具有三明治结构[33-35].HfS2相关晶体管具有优异的电流开关比(约107),并具有超过890 A/W 的超高光响应[36].HfS2纳米片可以作为一种潜在的水分解光催化剂[37,38].Graphene/HfS2异质结[39]用于电池电极,具有较高的充放电效率.WTe2/HfS2异质结[40]为Ⅲ型能带对齐,可用于隧道场效应晶体管.

As 单层与HfS2单层具有优异的光电性质,但它们的相关异质结尚未被研究,因此,本文设计As/HfS2异质结,并利用密度泛函理论系统地研究其几何结构、电子性质、光学性质以及量子调控效应.计算发现: 本征As/HfS2异质结为Ⅱ型半导体,且带隙相对两单层明显减小,特别是较大的价带偏移和导带偏移有利于研发高性能光电器件和太阳能电池.垂直应变能有效调节异质结的能带结构,特别是带隙.外加电场可以灵活地调控异质结的带隙及能带对齐方式,使异质结实现Ⅰ型、Ⅱ型和Ⅲ型之间的转变.另外,As/HfS2异质结在可见光区有较高的光吸收能力,且可以通过外加电场和垂直应变获得进一步提高.

2 计算方法

单层及异质结的几何优化、结构稳定性的评估、电子及光电特性的计算均利用基于密度泛函理论(DFT)的第一性原理方法,并在Atomistix Tool Kit (ATK)[41]软件包中实现,此软件包已广泛用于纳米结构的计算[42-48].为了求解Kohn-Sham 方程,用Troullier-Martin 模守恒赝势表示原子实对价电子的作用以及原子轨道的线性组合展开价电子波函数,基函数组选用DZP(double ζ+polarization).考虑杂化函数HSE06 计算其精度高于广义梯度近似(GGA)中的PBE 计算,本文电子结构计算均采用HSE06 函数.同时,我们利用Grimme的DFT-D2 函数修正异质结层间的范德瓦耳斯(vdW)作用[49].计算的能量截断半径(mesh cutoff)设为150 Ry (1 Ry=13.6056923 eV),简约布里渊区的在x,y,z方向上的k点取样采用21×21×1网格,其中x和y方向为二维晶体周期性延伸方向.与二维晶体垂直的z方向设置25 Å (1 Å=0.1 nm)真空层,以消除模型和“像”的相互作用.几何结构弛豫收敛标准为原子间相互作用力小于0.01 eV/Å以及晶格之间的应力小于0.01 GPa.能量收敛标准为10-5eV.所有的计算都在几何结构优化之后进行,为简单起见,体系的费米能级设置为零.

3 结果与讨论

3.1 As/HfS2 异质结构建及稳定性

As 和HfS2单层的原子结构如图1(a),(b)所示,As 单层(见图1(a))为六边形蜂窝状褶皱结构.本文优化的晶格常数为3.62 Å,褶皱高度为1.41 Å.HfS2单层(见图1(b)),有着与其他过渡金属硫化物类似的“三明治”结构,即Hf 原子平面夹在两个S 原子平面之间,优化的Hf—S 键长为2.55 Å,晶格常数为3.65 Å,单层高度为2.85 Å.这两个单层的优化几何参数,与之前的报道一致[50,36,40,51].As和HfS2单层的能带结构如图1(c)—(f)所示.利用PBE 计算,发现As 单层为间接带隙为1.64 eV 的半导体(图1(c)),HfS2则为直接带隙为1.29 eV 的半导体(图1(d)).而HSE06 计算表明: As 单层为间接带隙为2.32 eV 的半导体(图1(e)),而HfS2的带隙为直接带隙为2.04 eV 的半导体(图1(f)).显然,HSE06 计算的带隙比PBE 计算的结果高出0.7 eV 左右,即PBE 计算低估带隙,这是PBE 计算普遍存在的问题,但HSE06 计算与实验结果更为接近[32,36,51],因此在后续计算中,采用HSE06 函数计算体系的电子结构.

采用2×2 的As 层超胞(包含7 个原子)和2×2 的HfS2层超胞(包含11 个原子)构建As/HfS2范德瓦耳斯异质结,其晶格失配率约为1%,较小的晶格失配能避免较大的晶格应变的发生,使计算结果更加接近真实的实验情况.对于As/HfS2范德瓦耳斯异质结,可将HfS2单层视为固定不动的衬底,As 单层置于上面,且可通过平移和旋转调整As 原子相对HfS2单层的位置,得到对齐方式不同的异质结.考虑6 种堆垛方式,命名为A1—A3及B1—B3,如图1(g)—(l)所示,其中A1为As 单层的下层左边As 原子位于HfS2单层的上层S 原子正上方;A2为As 单层的下层左边As 原子位于HfS2单层的中间层Hf 原子正上方;A3为As 单层的下层一个As 原子位于HfS2单层的上、中层Hf—S键中心的正上方.对于B1—B3,考虑将As 单层沿与单层垂直的z轴旋转180°,并通过在HfS2单层平面上平移而获得,其中B1为As 单层的上层As原子位于HfS2单层中层Hf 原子的正上方,B2为As 单层的上层As 原子位于HfS2单层的上层S 原子的正上方,B3为As 单层的上层As 原子位于HfS2单层的上、中层Hf—S 键中心的正上方.

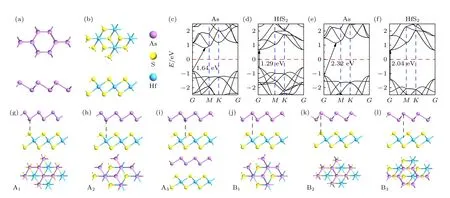
图1 (a) As 单层正视图和侧视图;(b) HfS2 单层正视图和侧视图;(c) PBE 计算的As 单层能带结构;(d) PBE 计算的HfS2 单层能带结构;(e) HSE06 计算的As 单层能带结构;(f) HSE06 计算的HfS2 单层能带结构;(g)—(l) As/HfS2 异质结的6 种堆叠方式,分别称为A1—A3 和B1—B3Fig.1.(a) Top and side view of As monolayer;(b) top and side view of HfS2 monolayer;(c) band structure of As monolayer by PBE calculation;(d) band structure of HfS2 monolayer by PBE calculation;(e) band structure of As monolayer by HSE06 calculation;(f) band structure of HfS2 monolayer by HSE06 calculation;(g)—(l) six stacking for As/HfS2 heterostructure,called as A1—A3 and B1—B3, respectively.

为了检验这6 种堆垛的能量稳定性,在结构优化后计算它们的结合能,定义为

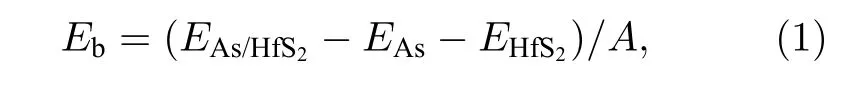
其中EAs/HfS2为As/HfS2异质结的总能量,EAs,EHfS2分别为As 单层及HfS2单层的总能量,A为异质结的面积.计算结果如表1 所列.显然,结合能分布在—8.81— —16.19 meV/Å2范围内,均为负值,表明无论哪一种堆垛,对应的异质结都是稳定的.同时可以看出不同堆垛的结合能相差较大,这意味着As 层在HfS2层上面较难自发滑动.计算的6 种堆垛的层间距也列于表1 中,其值落在3.0—3.6 Å之间,明显大于As 原子与S 原子的共价半径之和,即本文设计的结构的确是在As/HfS2界面没有化学成键的范德瓦耳斯异质结.从表1 还可以看出结合能随层间距的变化规律,即大(小)的层间距对应高(低)的结合能,这是容易理解的,因为层间范德瓦耳斯作用主要表现为吸引力,层间距越小,意味吸引力越大,所以结合能越低,体系越稳定,如层间距为最小值3.0Å时,异质结B2具有最低的结合能—16.19 meV/Å2,即B2为最稳构型的异质结.因此,下文研究选取B2为代表研究其电子及光学性质.

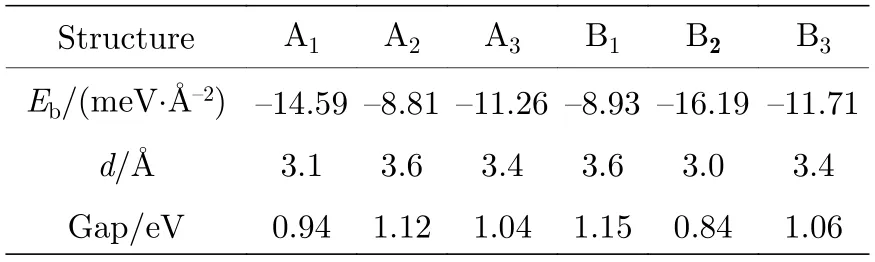
表1 不同堆叠异质结的结合能、层间距和带隙Table 1. The binding energy,interlayer spacing and band gap for various stacking configurations.

为了更直观地呈现所研究结构的成键特性,计算As 单层、HfS2单层及相关异质结(B2)的电子局域函数(ELF),如图2(a)所示.红色对应的ELF值接近1,为高度局域的电子分布,而蓝色对应的ELF 值接近0,表明电子在这些区域是高度离域的,所以ELF 图可用于确定成键类型.显然,无论是As 单层、HfS2单层或相关异质结,共价键都发生在单层内,异质结层间无共价结合,即层间为范德瓦耳斯结合.

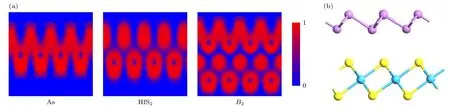
图2 (a) As 与HfS2 单层以及As/HfS2 异质结的电子局域函数(ELF);(b) B2 堆叠的Forcite 淬火的分子动力学模拟以检验结构的热稳定性Fig.2.(a) The electronic localization function (ELF) of As and HfS2 monolayers and As/HfS2 heterostructure;(b) Forcite quenching molecular dynamics simulation for the B2 stacking to examine the structural thermal stability.

为了检验异质结的热稳定性,对优化后的B2异质结进行Forcite 淬火分子动力学模拟,执行5 个退火循环,每个退火循环初始温度设置为300 K,最高温度为500 K,将300—500 K 分为6 个温度梯度,每个温度梯度设置120 个动力学步数,通过7.2 ps 退火循环处理,结果如图2(b)所示.显然异质结并未发生显著的结构变形或局部重组,仍保持优化后结构的完整性,说明本文研究的模型具有优良的热稳定性.

3.2 异质结电子结构

图3(a)所示为HSE06 计算的B2异质结的投影能带结构以及原子和轨道投影态密度.可见,B2异质结为准直接带隙半导体,其带隙约为0.84 eV,明显小于As 和HfS2单层的带隙(＞2.0 eV).见图1(e)—(f),也计算了其他堆垛的As/HfS2的带隙(见表1),其值落在0.94—1.15 eV 范围,显然,都比As 和HfS2单层的带隙小很多.众所周知,小带隙半导体材料有利于光的吸收及研发光学器件.从图3(a)还可以看出,VBM(价带顶)由As 层所贡献,CBM(导带底)由HfS2层所贡献,且轨道杂化较弱,表现为II 型能带对齐,这能有效促进电子-空穴对在空间上高效分离,从而抑制载流子复合,能够用于研发高效的光电器件[19,52]和太阳能电池[53].图3(a)中的原子投影态密度表明: 异质结的CBM 主要由Hf和S 原子的轨道组成,而VBM 处除少量S 原子态外,主要由As 原子的轨道组成.图3(a)轨道投影态密度表明: VBM 处少量的杂化情况是S 原子的3p 轨道与As 原子的4p 轨道能量较为接近,从而发生轨道杂化.图3(b)给出了异质结CBM 及VBM的Bloch 态(图3(b)),进一步证实VBM 态定域在As 层,而CBM 态分布于HfS2层.

为了解异质结的能带对齐的物理机理,图3(c)给出了异质结B2的能带对齐情况.As 单层的功函数WAs=—3.79 eV,而HfS2单层功函数WHfS2=—4.90 eV,所以As 单层的功函数低于HfS2单层,意味着当两个单层材料形成异质结时,电子将从As 层流向HfS2层,空穴从HfS2层扩散到As 层,使得HfS2单层和As 单层的费米能级分别上移和下移,同时形成内建电场,其方向为As 层指向HfS2层.最终体系平衡后,异质结的功函数WAs/HfS2=—4.33 eV,且实现了Ⅱ型能带对齐.此外,能带偏移情况也是衡量光电子器件性能的重要指标,导带偏移(CBO,即As 单层与HfS2单层的CBM 之差)和价带偏移(VBO,即As 单层与HfS2单层的VBM 之差)分别为1.48 eV 和1.31 eV.大的CBO 及VBO 值有利于光生电子从As 单层的导带流向HfS2层的导带,以及空穴从HfS2价带转移到As 层价带,既保证了光生电子-空穴的空间有效分离,也延长了层间激子的寿命.

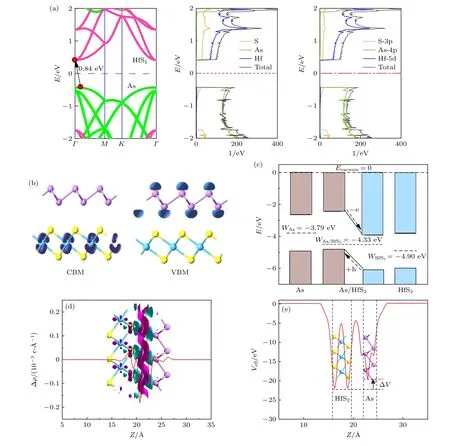
图3 (a) As/HfS2 异质结投影能带结构及投影态密度;(b) CBM 与VBM 的Bloch 态,等值面为0.035 e/Å3;(c) As/HfS2 异质结能带对齐;(d) 沿z 轴电荷密度差及三维电荷密度差,红色和蓝色分别代表电荷积累和消耗,等值面为3.5×10—4 e/Å3;(e) 沿z 轴方向有效势(eV)分布Fig.3.(a) Projected band structure and projected state density of As/HfS2 heterostructure;(b) Bloch state for CBM and VBM,the isosurface is set to 0.035 e/A3;(c) band alignment for As/HfS2 heterostructure;(d) charge density difference along the z-axis and three-dimensional charge density difference,red and blue respectively represent charge accumulation and depletion,the isosurface is set to 3.5×10—4 e/Å3,and (e) electrostatic potential distribution along the z-axis.

为进一步分析其电荷的分布,还计算了异质结B2沿z轴方向的电荷密度差,定义为

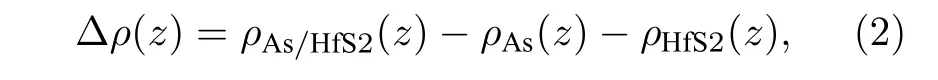
其中ρAs/HfS2(z) ,ρAs(z)和ρHfS2(z) 分别为异质结、As 单层、HfS2单层在z点的电荷密度,正值和负值分别表明该区域积累和失去电荷.同时也计算三维电荷密度差,定义为

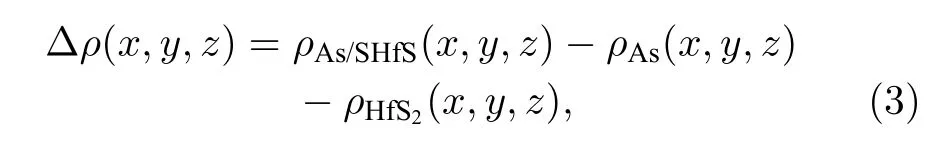
其中ρAs/SHfS(x,y,z) ,ρAs(x,y,z) 和ρHfS2(x,y,z) 分别为异质结、As 层、HfS2层在(x,y,z)点的电荷密度,计算结果如图3(d)所示,其中红色代表电荷的积累,绿色代表电荷的减少.总体上讲,HfS2层得到电子,As 层失去电子,并且在层间出现了明显的电荷累积(层间电偶极子).

图3(e)所示为异质结的有效势分布,可以看到HfS2中的势阱几乎对称地分布在两S 原子层,这是因为Hf 原子的电负性低于S 原子,所以Hf 原子层的电子转移到两S 原子层,且通过势阱来禁锢电子.As 原子层也有明显的势阱用于禁锢电子.As 层势阱底比HfS2层势阱底高出一个值ΔV,这意味着As 层电子能向HfS2层隧穿.在异质结界面处存在一个高而宽的势垒阻止电子隧穿,所以层间转移的电子数量是较少的,这与计算的电荷密度差完全一致(图3(d)).

3.3 垂直应变效应

本节研究垂直应对变异质结B2电子性质的影响.垂直应变定义为:ε=d-d0,其中d为施加应力后的层间距,d0为优化平衡层间距,因此ε的正(负)表示对异质结施加的是拉伸(压缩)应变.图4(a)红色曲线为异质结结合能随应变变化情况,能量最低点为应变为ε=0 时的情况.当拉伸或压缩发生时,结合能增大,即系统的能量稳定性受到明显影响,这是可以理解的.特别是压缩发生后,结合能迅速增大,这是因为随着层间距减小,两单层原子之间静电排斥力快速上升.而拉伸过程中,结合能缓慢增大,这是因为随着层间距增大,两单层原子之间静电吸引力缓慢提升的结果.图4(a)绿色曲线呈现异质结的带隙随应变的演化,其中绿色实心圆表示间接带隙,空心圆表示直接带隙.可以看出,拉伸时带隙先迅速增大,且在ε=0.3 Å后,带隙缓慢增大.有趣的是,在ε=0.3 Å这个转折点后,异质结出现间接带隙到直接带隙的转变.而压缩时带隙迅速减小,当ε=—0.8 Å时出现半导体到金属(黄色空心三角形表示金属)的过渡.总之,从ε=—0.8 Å到ε=0.8 Å过程来看,异质结的带隙随层间距增大单调增大,且出现间接带隙到直接带隙的转变.为了了解这些变化的细节,如图4(c)给出了ε=±0.8 Å,±0.3 Å及±0.1 Å时的能带结构.显然,CBM 始终位于G点,但对应的能量位置随层间距增大不断向上移动,而VBM 态(红色圆点)位于G—M之间,但对应的能量位置随层间距增大不断向下移动,从而导致异质结的带隙随层间距增大而单调增大.特别是随着层间距增大,VBM态也不断向G点移动,在ε=0.3 Å处,VBM 态刚好位于G点,从而导致直接带隙的出现,并持续到ε=0.8 Å.

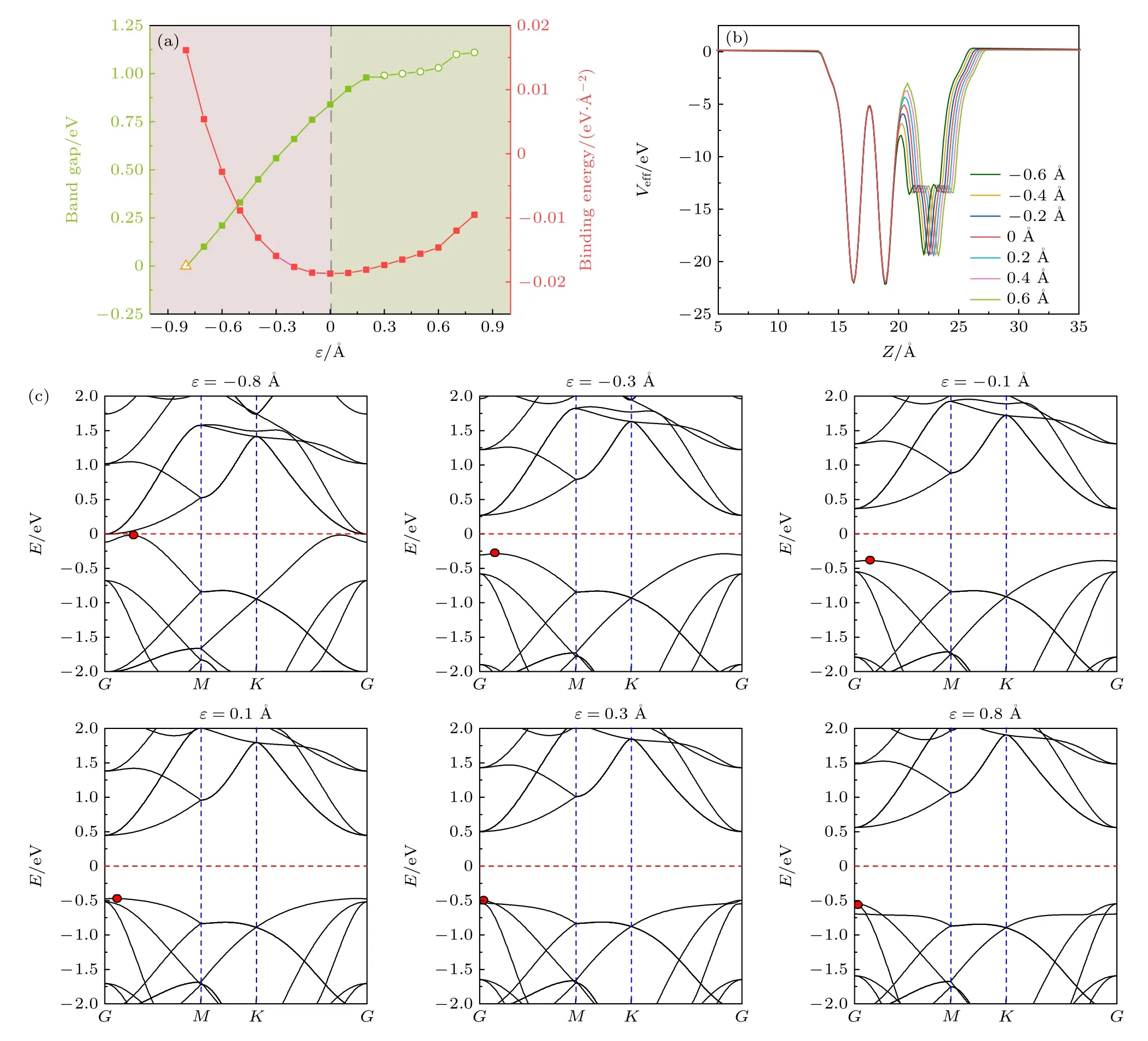
图4 (a)带隙及结合能随应变的变化;(b) 应变 ε=—0.6,—0.4,—0.2,0,0.2,0.4,0.6 Å 时有效势的变化;(c) 应变ε=—0.8,—0.3,—0.1,0.1,0.3,0.8 Å 时异质结的能带结构,最高导带上的红点代表VBM 的位置Fig.4.(a) Band gap and binding energy changes with strain;(b) the effective potential distribution along z-axis at ε=—0.6,—0.4,—0.2,0,0.2,0.4 and 0.6 Å,respectively;(c) the As/HfS2 band structure at ε=—0.8,—0.3,—0.1,0.1,0.3 and 0.8 Å,respectively,the red dot at top conduction band indicates the VBM position.

为了理解带隙及整个电子结构随层间距的变化,计算了异质结的层间距依赖性的有效势分布,如图4(b)所示,可以看出,层间距对界面势垒具有明显的调控效应,即拉伸后,随着层间距的增大,层间势垒增大,而压缩时,随着层间距的减小,层间势垒减小.这些变化导致两单层的静电势能差随层间距变化.如前所述,CBM 与VBM 位于两层不同的材料,所以导致CBM 与VBM 随层间距相向或相反移动,即带隙变化.能带结构随层间距变化也与层间电子转移密切相关,所以我们计算了ε=—0.6,—0.2,0.2 及0.6 Å时的三维电荷密度差,如图5 所示.可以看出压缩(拉伸)时,有较多(少)的电子转移,这与层间距减小(增大)使层间势垒变小(大)密切相关,因为小的层间势垒更有利于电子的转移.不同层间距,电荷转移不同,使得层间内建电场不同,进而使异质结内静电势分布不同,从而导致差异性的能带结构.

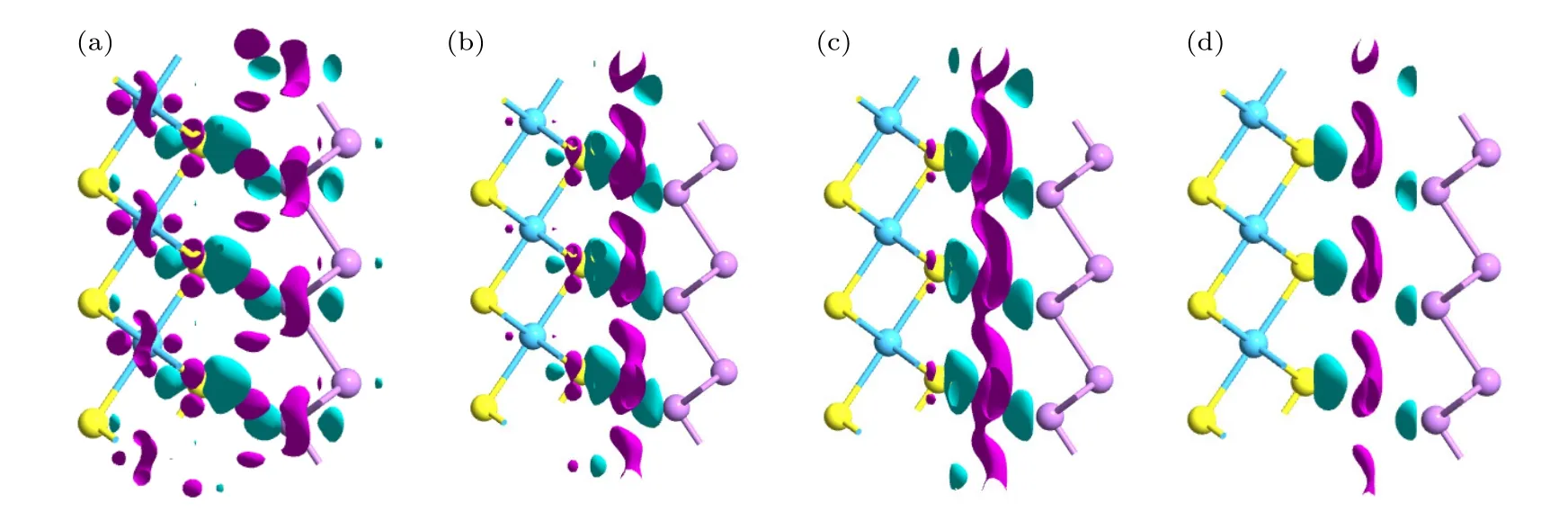
图5 不同垂直应变时的三维电荷密度差 (a) ε=—0.6 Å;(b) ε=—0.2 Å;(c) ε=0.2 Å;(d) ε=0.6 ÅFig.5.Three dimensional charge density difference at (a) ε=—0.6 Å,(b) ε=—0.2 Å,(c) ε=0.2 Å,(d) ε=0.6 Å,respectively.

3.4 电场调控

外加电场是调控异质结电子结构的有效方法之一[54].本文施加一个垂直外电场Eext,其正方向定义为As 层指向HfS2层(与内建电场同相),如图6(a)所示,反之,称为反(负)方向电场.图6(b),(c)所示分别为计算的异质结带隙和两单层带边(CBM 及VBM)随电场的变化曲线.可以看出,当正向电场满足0≤Eext≤0.95 V/Å时(图中Ⅲ区),异质结带隙随电场单调增大,此时VBM 由As 层所贡献,CBM 由HfS2层贡献,保持II 型能带对齐;当外电场满足 0.95 V/Å＜Eext≤ 1.2 V/Å时(Ⅳ区),带隙保持不变,VBM 和CBM 均由HfS2层贡献,这时异质结是转变为I 型能带对齐;当电场Eext＞1.2 V/Å(Ⅴ区),带隙单调减小,VBM 由HfS2层贡献,CBM 由As 烯层贡献,右转变为II 型能带对齐.施加反向电场时,当电场在—0.8 V/Å＜Eext≤0 V/Å的范围内(Ⅱ区),带隙随反向电场增大而单调变小,但仍为Ⅱ型能带对齐;在—1.2 V/Å＜Eext＜—0.8 V/Å区间(Ⅰ区),带隙变为0,表现为Ⅲ型能带对齐.总之,外加电场可以灵活调控异质结的带隙及能带对齐方式,能使异质结实现Ⅰ型、Ⅱ型和Ⅲ型之间的转变.不同能带对齐方式,异质结有不同的应用,例如: Ⅰ-型异质结能使电子和空穴高效复合,可应用于纳米光电器件;Ⅱ-型异质结有利于肖特基场效应晶体管、压电效应等方面的应用;Ⅲ-型异质结在隧穿场效应管方面具有重要的应用前景.因此,带隙及能带对齐方式可调的异质结,在电子及光电子领域具有巨大的应用潜力.

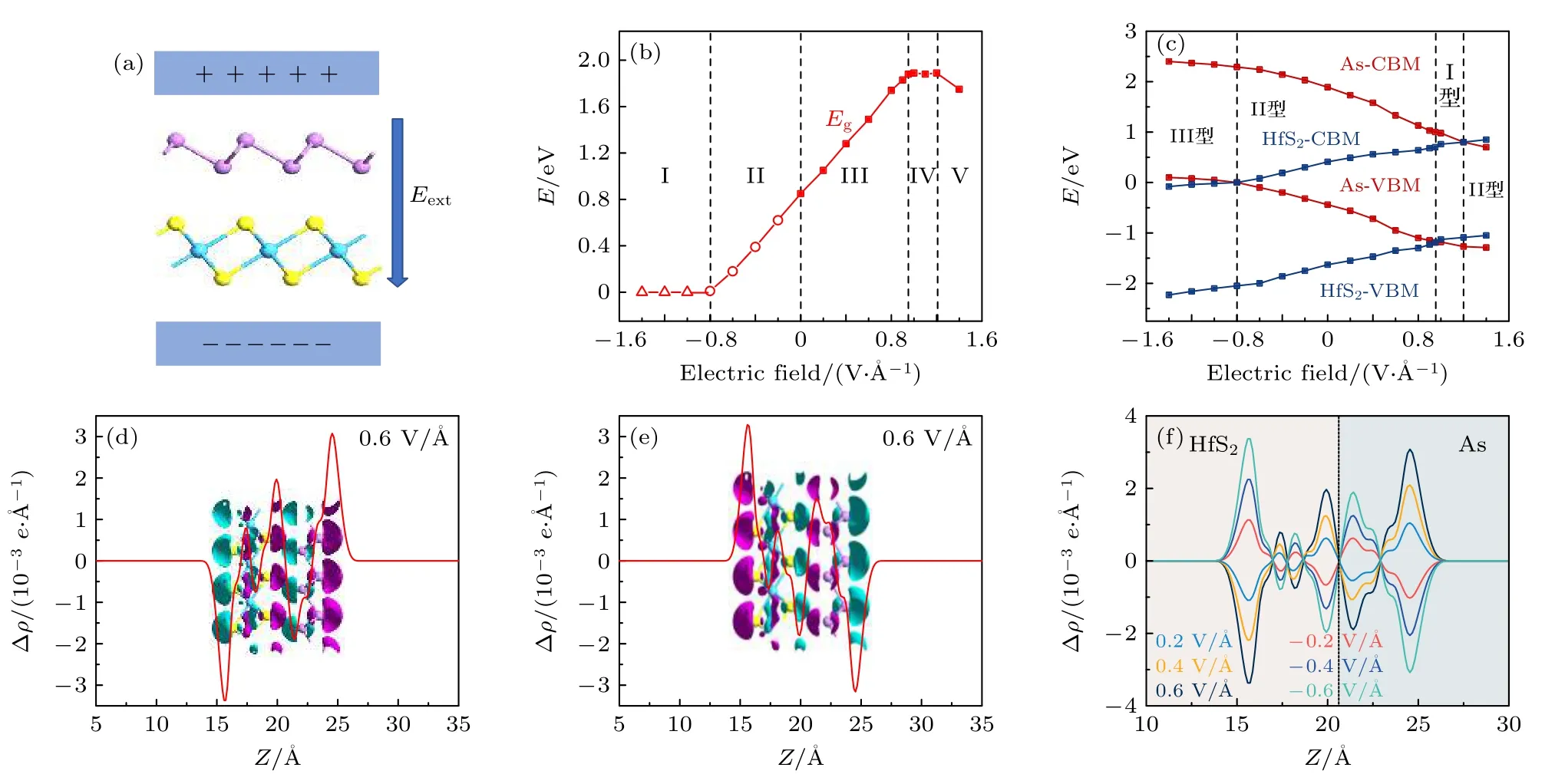
图6 (a) 异质结外加电场方向示意图;(b)异质结带隙随外电场变化;(c) As 与HfS2 单层带边(VBM 及CBM)位置以及能带对齐方式随外电场的变化;(d) 0.6 V/Å电场时,异质结的电荷密度差;(e) —0.6 V/Å电场时,异质结的电荷密度差;(f) 异质结电荷密度差随电场的变化趋势Fig.6.(a) Schematic diagram of applied external electric field on heterostructure;(b) band gap variation of heterostructure with electric field;(c) evolution of band edges (VBM and CBM) for As and HfS2 monolayers and heterostructure and its band alignment manner with electric field.The charge density difference of heterostructure at: (d) Eext=0.6 eV/Å,(e) Eext=—0.6 eV/Å,and(f) various electric field.

图6(c)中两单层带边(CBM 及VBM)随电场的变化是很容易理解的.施加外电场导致两单层产生局部静电势能差: ΔEsp=qEextd0,d0为平衡层间距.当电场为正向时,HfS2单层的局部静电势能升高,所以其CBM 及VBM 向上移动,而As 单层的局部静电势能降低,所以其CBM 及VBM 向下移动.当施加反向电场时,情况恰恰相反,即As 单层的局部静电势能高于HfS2单层的局部静电势能,因此随着电场反向增大,其CBM 及VBM移动的方向与正向电场时相反.这样能看到两单层的CBM 及VBM 随电场(无论正负)是单调变化的.由于两单层的CBM 及VBM 随电场变化的4 条曲线存在交叉点,从而分成了多个区域(见图6(c)),所以出现了外电场依赖性的不同能带对齐类型,即出现Ⅰ型、Ⅱ型和Ⅲ型的能带对齐.

为进一步了解在电场作用下异质结电荷的转移情况,计算了不同电场下异质结沿z-方向的电荷密度差及3D 电荷密度差,如图6(d)—(f)所示.可以看到当Eext=0.6 V/Å时,As 层获得电子,而HfS2层去失电子(图6(d));在Eext=—0.6 V/Å时,情况恰恰相反,即As 层去失电子,HfS2层获得电子(图6(e)).这是由于外加电场远大于内建电场,所以电子在外电场作用下的漂移移动起决定作用,在正(负)向电场的作用下,电子从HfS2(As)层漂移到As(HfS2)层.其他电场作用下,两单层得失电子的情况与Eext=±0.6 eV/Å相同,仅仅只是转移数量上的区别,显然,电场越强(无论正或负方向),电荷转移(漂移)越明显.

3.5 光学性质

一般来说,由于带隙减小,Ⅱ型异质结的光吸收能力相比于各单层材料会提升.光吸收系数α表征光穿过物体每经过单位长度能量被吸收的比例,可由动态介电响应函数ε(ω)求得:

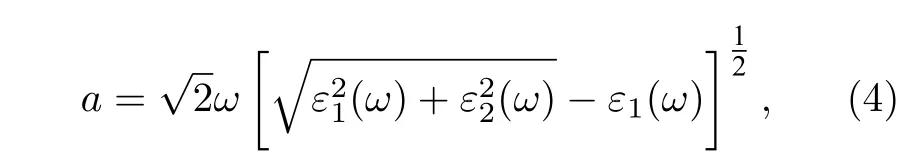
其中ε1(ω) 和ε2(ω) 分别代表介电函数ε(ω) 的实部和虚部.介电常数的实部表示宏观的极化程度,虚部表示介电效应发生时的损耗.光吸收系数随能量的变化如图7 所示.计算发现光吸收是平面上各向同性的,但在垂直方向上吸收系数不同,分别用αII及α⊥表示.

图7(a),(b)分别为 As 单层、HfS2单层和异质结在垂直和平行方向上的吸收光谱,并以能量为自变量(能量范围在1.64—3.19 eV 为可见光,大于3.19 eV 为紫外光,小于1.64 eV 为红外光).其中红色曲线为As 单层的光吸收系数,绿色曲线为HfS2单层的光吸收系数,黑色曲线为 As/HfS2异质结的光吸收系数.由此可知,As 单层在垂直方向上(α⊥)仅能吸收部分紫外光谱,几乎不能吸收可见光和红外光;而平行方向上(αII)对紫外光有较强的吸收.对于HfS2单层,不管是在平行方向还是垂直方向,其主要吸收位置皆为紫外和部分可见光区域.构建异质结后,其在可见光和红外光区域的光吸收能力(αII及α⊥)比单层材料显著提高.特别是当垂直照射时,在能量为1.82 eV(红光)、2.50 eV(绿光)、3.00 eV(紫光)、3.86 eV(紫外光)和4.58 eV(紫外光)处具有吸收峰,且达到104,这些吸收峰来源于电子的带间跃迁.平行方向上,在可见光区域的光吸附也有一定的提高,达到105.总之,异质结对可见光的吸收能力明显提高.众所周知,在太阳光谱中,紫外光谱所占的能量比例是最少的(约5%),可见光和红外光占了绝大部分,这就意味不管在垂直方向还是平行方向,As/HfS2异质结对太阳能的吸收与转化能力有明显提高.

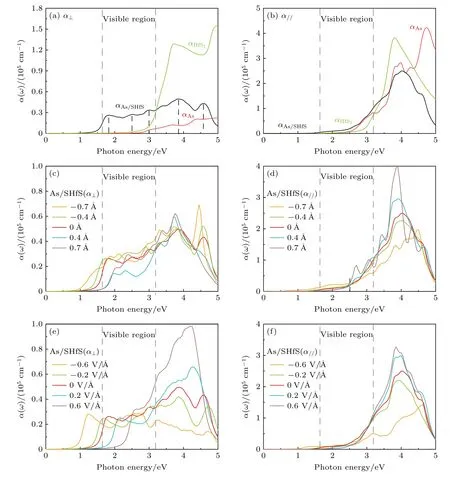
图7 光吸收系数及调控效应 (a),(b)单层及本征异质结;(c),(d)应变调控的异质结;(e),(f)电场调控的异质结Fig.7.Light absorption coefficients and tuning effects: (a),(b) The monolayer and intrinsic heterostructure;(b),(c) strain tuning effects;(e),(f) the electric field tuning effects .

为进一步了解量子调控对光吸收的影响,分别计算了施加层间应变及外加电场时的光吸收系数.图7(c),(d)所示为光吸收系数的层间应变效应,当垂直压缩异质结时,无论是在垂直方向还是平行方向上,光的吸收边相对于未压缩异质结的吸收边发生了明显的红移,并且在绿光(2.51 eV)到紫外的范围内,平行方向上光吸收能力相比未压缩时显著提升;当拉伸层间距时,垂直方向上吸附边红移,而在平行方向上,大约在绿光(2.51 eV)到紫外的范围内,光吸收能力相比未压缩时略有减小,但在红外到绿光的范围内,光吸收能力提升.图7(e),(f)所示为光吸收系数的外电场效应,可以看出,不管是平行还是垂直方向,负向电场都可以使吸附边红移,正向电场使吸附边蓝移.因此,负向电场使异质结对红外光吸收范围和强度增大,正向电场使异质结对紫外光的吸收强度上升.

4 总结

本工作考虑了6 种堆叠方式构建As/HfS2范德瓦耳斯异质结,并选取最稳结构,利用基于密度泛函理论的第一原理方法系统研究了电子和光学性质以及量子调控效应.计算发现,本征异质结为Ⅱ型能带对齐半导体,其带隙为约0.84 eV,相对两单层(带隙＞2.0 eV)明显缩小,特别是导带偏移(VBO)和价带偏移(CBO)可分别高达1.48 eV和1.31 eV,能有效促进电子-空穴对在空间上高效分离,从而有效抑制载流子复合,有利于研发高效的光电器件和太阳能电池.垂直应变能有效调节异质结的能带结构,拉伸时带隙增大,并出现间接带隙到直接带隙的转变,而压缩时带隙迅速减小直到金属相发生.外加电场可以灵活地调控异质结的带隙及能带对齐方式,使异质结实现Ⅰ型、Ⅱ型和Ⅲ型之间的转变.另外,As/HfS2异质结在可见光区有较高的光吸收能力,且可以通过外加电场和垂直应变获得进一步提高.这些理论预测表明,As/HfS2异质结具有优异的物理特性以及灵活可调的电学和光学特性,在纳米电子及光电器件应用方面具有重要的应用潜力.