铁电极化翻转对硅烯异质结中电子性质的调控*

丁俊 文黎巍 李瑞雪 张英

1) (河南工程学院理学院,郑州 451191)

2) (北京师范大学物理系,北京 100875)

硅烯是硅原子蜂窝状排列构成的二维材料,由于其层内硅原子不在同一平面上而易受到电场等调控,近年来成为理论和实验研究的一个热点.借助于第一性原理计算方法,详细研究了硅烯和二维铁电材料In2S3单层材料异质结的堆垛形式和电子结构.计算结果表明,硅烯和 I n2S3 可以形成稳定的异质结,I n2S3 衬底的自发铁电极化对硅烯能带有显著调控作用.铁电极化方向向上时,自发极化电场和衬底的共同作用在狄拉克点打开能隙,K 和K′点贝利曲率符号相反,对应能谷霍尔效应态.铁电极化方向向下时,硅烯和 I n2S3 之间间距变小,费米能级有能带穿过,对应金属态.研究结果对铁电调控硅烯二维异质结提供参考,为硅烯异质结在信息存储领域的应用指明方向.

1 引言

石墨烯是碳原子在二维六角格子上紧密排列形成,相邻碳原子之间形成sp2杂化轨道,π —π 键作用使得石墨烯的电子结构在布里渊区K和K′点形成狄拉克锥结构.六角格子还具有能谷自由度,具有很多特殊性质因而受到广泛关注,在一定条件下可以利用能谷自由度实现能谷分辨的电流控制,在能谷电子学领域得到应用[1].与石墨烯类似,硅烯是由单层硅原子在六角格子上排列形成的二维材料,但与石墨烯不同的是硅烯中原胞内的两个硅原子不再处于同一平面而形成翘曲结构,两个原子在垂直方向上有0.44 Å的高度差,这种翘曲结构导致硅烯具有介于sp2和sp3之间的杂化轨道,较强的面内 π —π 键仍然使其保持了狄拉克电子特性,面外的σ—π 键显著增强了自旋轨道耦合作用,使得硅烯可以实现量子化自旋霍尔效应[2,3].

石墨烯等二维材料没有能隙,而可调控的能隙是这类二维材料在设计和优化新型电子器件过程中的必备条件.普通半导体材料受限晶体结构,能隙基本不受电场影响,电场虽然不能在单层石墨烯能带狄拉克点打开能隙,但是在双层石墨烯里面,电场破环了AB子格子对称性,可以在双层石墨烯里面实现连续可调控的调控能隙变化,在石墨烯场效应管等纳米电子学器件研究方面有巨大潜力[4,5].对于硅烯,由于翘曲结构的存在,电场不但可以直接调控单层硅烯的能隙、狄拉克电子的质量,在不同的电场条件下还可以实现普通绝缘体和拓扑非平庸绝缘体之间的转变,在引入磁性后,电场还可以在硅烯中实现对自旋和能谷自由度的控制,实现电场调控能谷分辨的量子化反常霍尔效应、量子化自旋霍尔效应等拓扑态,加上硅烯与目前硅基微电子技术方面更好的兼容性,为硅烯在未来自旋电子学和能谷电子学应用方面奠定坚实基础[6-14].

由于硅烯不像石墨烯一样存在天然多层结构,所以不能采用机械剥离的方法来制备.多层大面积硅烯主要是通过在银等贵金属表面外延生长来制备[15,16],然而金属衬底并不利于硅烯在新型纳米器件中的应用.利用分子束外延技术,可以实现大面积单层硅烯在二维绝缘体 M oS2表面外延生长,开辟了非金属衬底生长硅烯的先河[17].最近,实验上已经实现利用石墨烯对硅烯进行保护并构筑稳定的石墨烯-硅烯异质结[18],为硅烯异质结器件应用重新注入活力.二维材料由于在一个方向上尺寸受到限制,本身就具有奇特性质,如果可以选用不同的二维材料堆叠形成异质结,就有可能成为研究更多新奇物理现象的平台.近年来大规模可控外延生长技术的进步,推动二维材料异质结的发展,目前已经在隧穿晶体管、光探测、发光二极管、自旋电子学等方面设计出性能优异的异质结器件[19,20].

铁电材料一般都是绝缘体,除了具有自发铁电极化,还有高介电系数、高压电系数等特点,被广泛用来作为衬底以调节二维材料性质.在衬底极化翻转过程中,可以实现对二维材料载流子浓度的调控,也可以构建铁电场效应管、铁电隧道结等,与拓扑材料构成的异质结中还可以实现对拓扑绝缘体的非易失、可逆调控[21-26].最近,二维铁电材料以SnTe,C uInP2S6,I n2Se3等为代 表受到 广泛关注,特别是 I n2Se3,不但同时具有面内面外耦合在一起的自发铁电极化,还可以在外电场作用下实现极化翻转[27-32].基于此,本文研究二维铁电材料与硅烯构成的异质结,探讨界面效应及铁电极化翻转对硅烯有什么影响.

2 研究方法

第一性原理计算采用基于密度泛函理论和投影缀加平面波赝势方法的VASP 软件包[33],计算中使用广义梯度近似(GGA) 处理电子与电子之间的交换关联相互作用[34].电子波函数采用平面波展开,平面波截断能取为400 eV,布里渊区K点网格采用12 × 12 × 1 Monkhorst-Pack 方案划分.在不同堆垛结构计算过程中保持晶格不变但所有原子都进行弛豫,弛豫过程采用共轭梯度方法寻找能量基态,力的收敛标准为0.005 eV/Å.为了正确处理二维材料层间较弱的相互作用,采用了DFTD3 范德瓦耳斯力修正方法[35],同时为了避免不同周期性结构之间相互作用,真空层选取约为20 Å.

3 结果与讨论

In2Se3是最近发现的III2VI3型二维铁电材料,是由层内Se-In-Se-In-Se 原子依次排列形成的五原子层单元通过范德瓦耳斯力作用堆垛形成的层状材料,其块体具有非中心对称的R3m结构,因此可以具有铁电极化.结构优化后稳定晶格常数为4.07 Å,I n2S3晶格常数为3.88 Å,硅烯的晶格常数为3.86 Å,并且 I n2S3也具有稳定的铁电结构和较强的面外电极化,考虑到晶格匹配因素,本文选取1 × 1 单层 I n2S3和硅烯构建异质结[2,36].单层In2S3的铁电极化为1.26 µ C·cm-2,与实验上观察到的In2Se3铁电极化0.92 µ C·cm-2较为接近[37].考虑硅烯/ I n2S3异质结的两种堆垛形式,如图1 所示,硅烯/ I n2S3异质结内最接近硅烯的In-S 原子也形成翘曲的六角格子,AA堆垛是这两个In 和S 原子刚好位于硅烯里面不同子格子对应硅原子下方,如图1(a)所示,图1(b)是侧视图,图中 I n2S3的自发铁电极化方向向上.AB堆垛对应In 原子在一个硅原子下方,而S 原子处于硅烯六角格子中心,图1(c)和图1(d)分别是AB堆垛的俯视图和侧视图.经过结构优化,AA堆垛和AB堆垛的层间距分别为4.30 和3.93 Å,与典型二维异质结层间距相当.AB堆垛还有可能是S 原子在一个硅原子下方,而In 原子处于硅烯六角格子中心,这种堆垛形式能量比图1 中AB堆垛高13.16 meV,后面只讨论图1对应的AB堆垛形式.

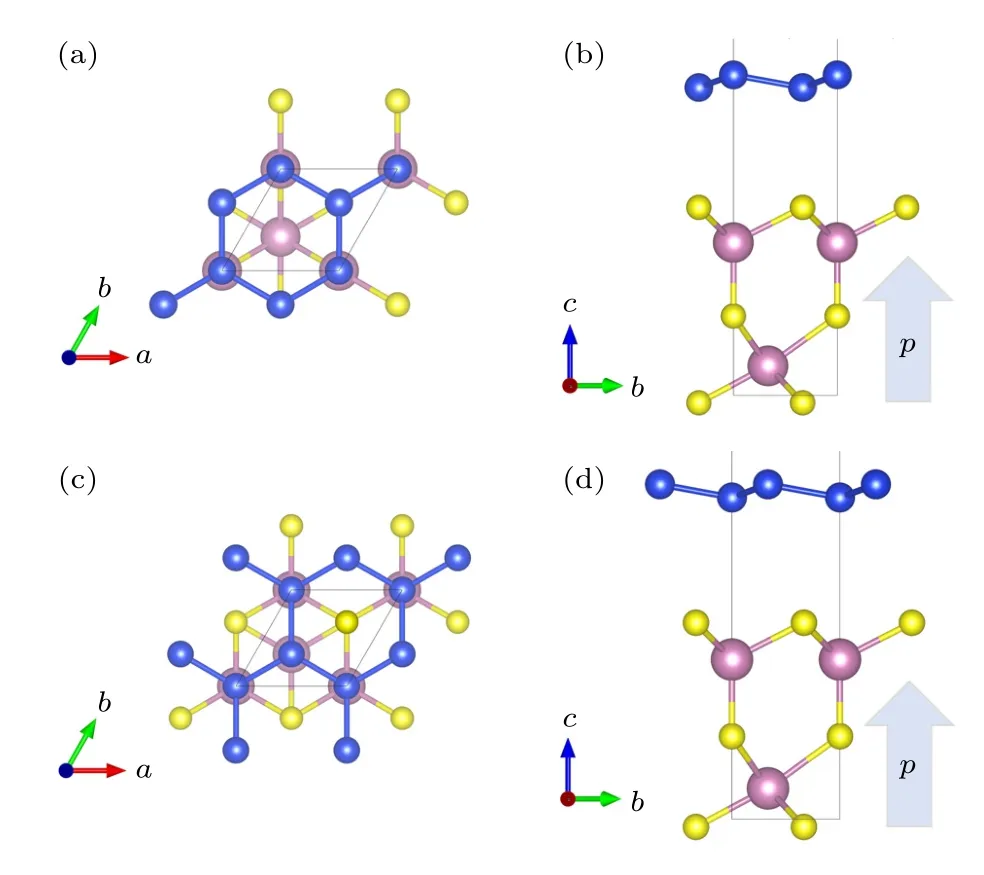
图1 硅烯与 I n2S3 异质结的结构图 (a),(b) AA 堆垛的俯视图和侧视图;(c),(d) AB 堆垛的俯视图和侧视图Fig.1.The structure of Silicene/ I n2S3 heterostructure:(a),(b) the top and side view of AA stacking;(c),(d) the top and side view of AB stacking.

计算结果表明,图1(c)所示AB堆垛具有最低能量,为了寻找界面相互作用能量最低点,计算了硅烯相对于 I n2S3平移时的堆垛能.堆垛能定义为硅烯和 I n2S3不同堆垛形式的能量与最稳定AB堆垛结构能量之差,分别沿原胞[110]和[100]方向平移硅烯,所得不同堆垛时能量如图2所示.硅烯相对于 I n2S3沿[100]方向平移,相当于沿In2S3五原子层单元中同一层内In-In 或者S-S 的最近邻方向平移.沿[110]方向的平移相当于沿 I n2S3五原子层单元中同一层内In-In 或者S-S 的次近邻方向平移,[110]方向也是极化翻转过程中S 原子在平面内的移动方向.这两个方向是两层之间在平面内平移的两个不等价的代表性方向,计算出沿不同方向平移的堆垛能与其他双层二维材料之间的堆垛能形状类似[31,38].图2 中AB堆垛时,硅烯相对于In2Se3沿[110]方向平移[2/3,2/3]即为AA堆垛,沿不同方向平移时的堆垛能曲线表明AB堆垛是最稳定的堆垛形式.

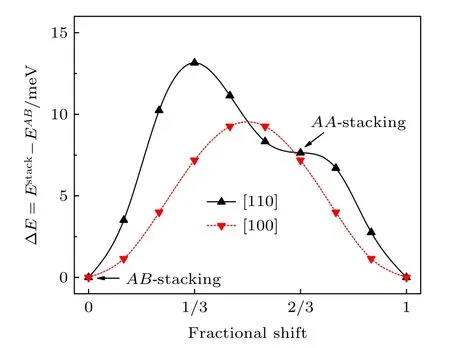
图2 沿晶体表面不同方向横向平移时堆垛能变化情况.图中给出沿[100](红色虚线)和[110](黑色实线)方向平移时堆垛能变化情况,AB 堆垛在平面内平移[2/3,2/3]即可得到AA 堆垛Fig.2.Stacking energy as a function of lateral shift with respect AB stacking.The stacking energy are shown both for[100] (dotted red line) and [110] (solid black line) directions.AB stacking corresponding to a fractional lateral shift of[2/3,2/3] of the top layer compared to AA stacking.

为了定量描述界面相互作用,计算了硅烯和In2S3之间的 吸附能,,其中ETot是异质 结的总能量,和ESi分别是In2S3和硅烯单独存在时的能量.分别考虑 I n2S3的自发铁电极化向上和向下两种情况,其吸附能和In2S3与硅烯之间层间距变化如表1所列. I n2S3极化方向向下时硅烯与 I n2S3之间层间距比极化方向向上时小0.31 Å,同时吸附能高24.65 meV,说明极化方向向下时硅烯与 I n2S3之间有较强相互作用,对应较低能量状态,与异质结总能计算结果极化向上比极化向下高22.87 meV 一致.吸附能计算结果与LiNbO3/石墨烯异质结22.3 meV 及双层石墨烯吸附能25.1 meV 基本相当[22,39],并且表现出显著的极化方向依赖性,预示着极化翻转可以对异质结性能起到较明显调控作用.

表1 I n2S3 极化方向改变时总能量,结合能以及层间距和能隙变化情况.能隙单位为meV,SOC 指考虑自旋轨道耦合后数值Table 1. Total energy,adhesion energy,layer distance and energy gap with the polarization of I n2S3 upward and downward.SOC refers to the energy gap (meV) calculated with spin-orbit coupling.

接下来研究 I n2S3极化翻转对异质结电子性质的影响.图3 给出了硅烯/ I n2S3异质结的能带图.当 I n2S3自发铁电极化向上时,硅烯和 I n2S3间距较大,为3.93 Å,层间相互作用较弱,自发极化电场及衬底的共同作用下破坏了硅烯中AB子格子对称性,硅烯能带在布里渊区K和K′点形成能隙,但费米能级仍然位于能隙中间.当 I n2S3自发铁电极化向下时,硅烯和 I n2S3间距变小为3.62 Å,层间相互作用明显增强,具体表现在硅烯能隙显著变大且价带上移穿过费米能级,意味着硅烯与 I n2S3之间出现电荷转移,以铁电极化向上时为参考,电荷转移大小是0.04e.计算结果表明 I n2S3极化翻转可以调控硅烯/ I n2S3异质结实现半导体-金属性转变,有望在新一代电子器件中得到应用.

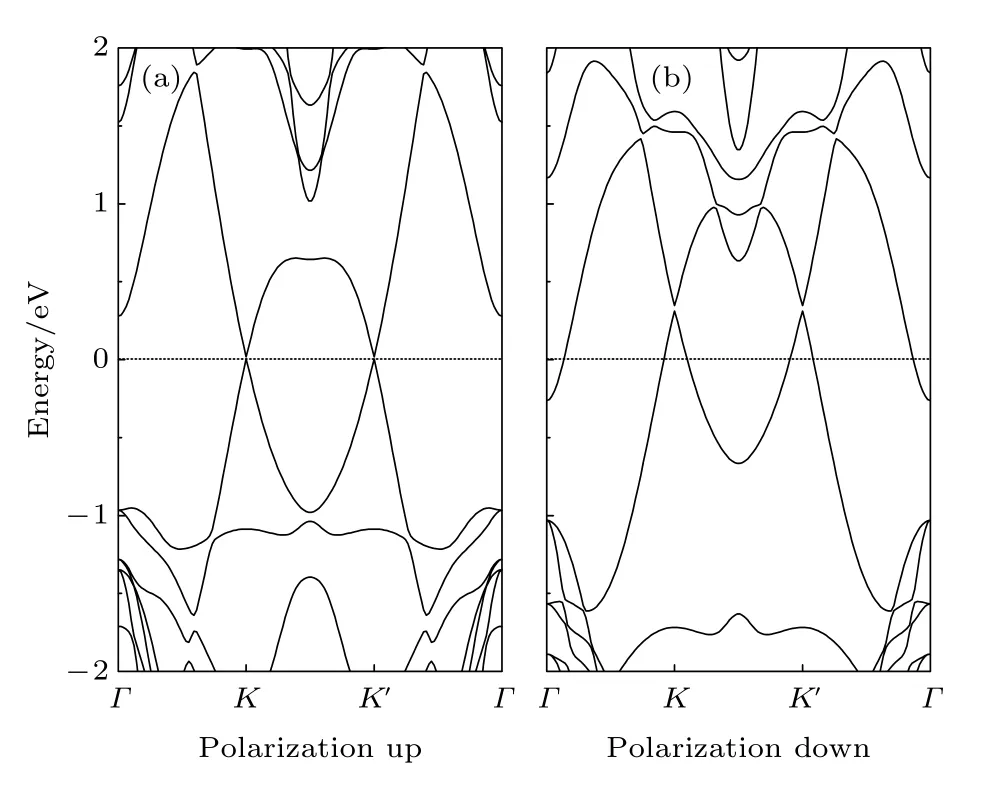
图3 硅 烯/ I n2S3 异质结 能带图 (a)和(b)分别对 应In2S3极化方向向上和向下Fig.3.Band structure of silicene/ I n2S3 heterostructure: (a)and (b) corresponding to the polarization of I n2S3 upward and downward,respectively.

由于硅烯中翘曲结构的存在显著增强了自旋轨道耦合作用,自由的硅烯可以实现量子化自旋霍尔效应[2].进一步考虑自旋轨道耦合效应对异质结能带的影响,图4 给出了布里渊区K和K′点附近能带的放大图.当 I n2S3自发铁电极化向上且不考虑自旋轨道耦合时,如图4(a)所示,K与K’点附近能带完全简并,能隙为13.6 meV,考虑自旋轨道耦合后(图4(b)),K与K′点附近能带劈裂,能隙减小为1.8 meV,费米能级仍然在能隙中.当 I n2S3自发铁电极化向下且不考虑自旋轨道耦合时,如图4(c)所示,能隙为33.3 meV,但是费米能级穿过导带,考虑自旋轨道耦合后能带略有降低,为30.8 meV(图4(d)).硅烯与衬底的相互作用破坏AB子格子对称性后可以实现能谷霍尔效应,可以用能谷陈数表征,CV=CK -CK′[1,40,41].CK/K′是陈数C在布里渊区K/K′附近非零范围内的积分数值.陈数C决定了量子化的霍尔电导σxy=Ce2/h,可以通过Kubo 公式计算[42,43]:

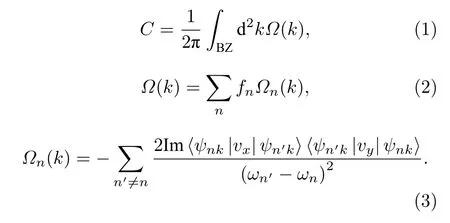
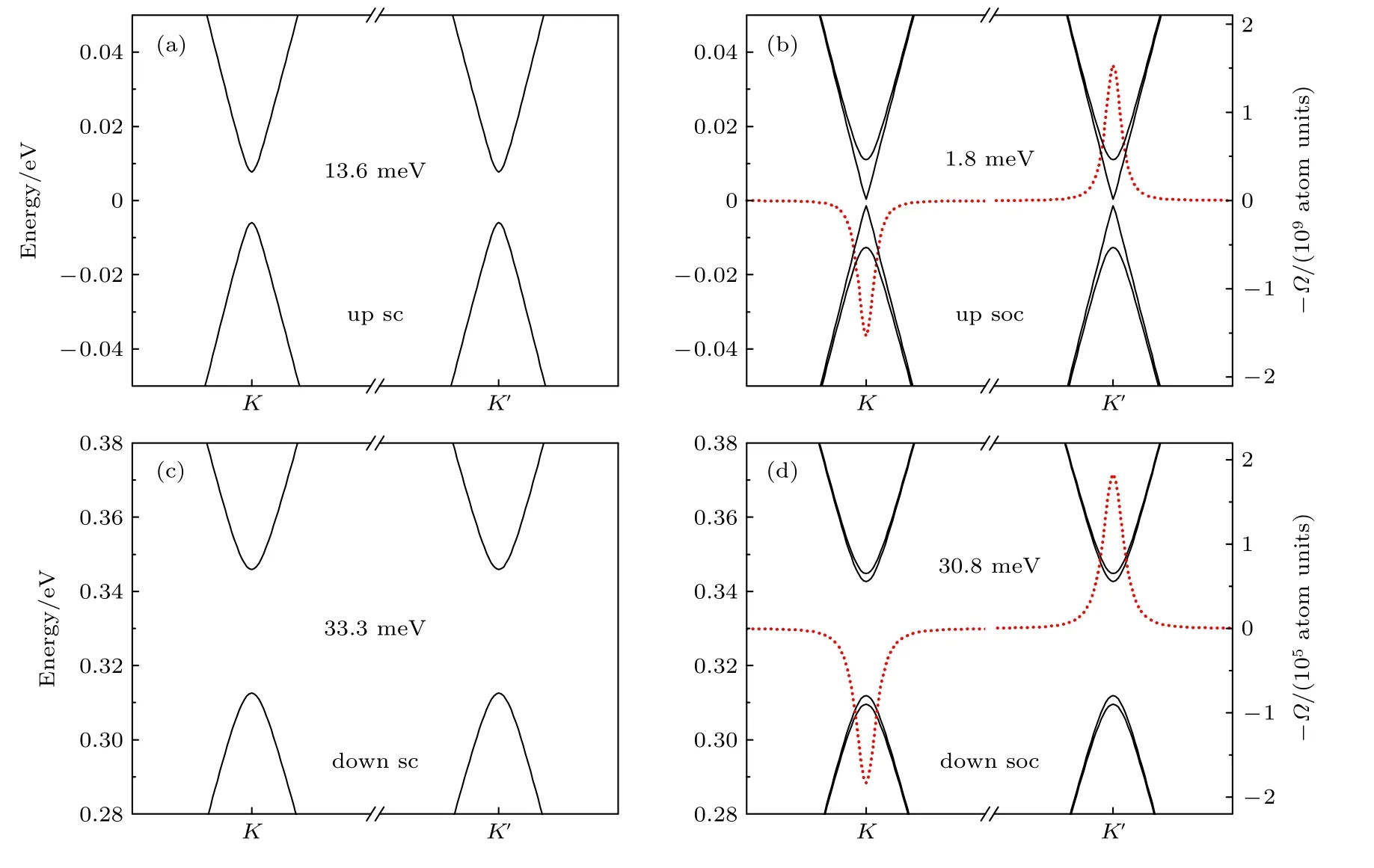
图4 硅烯/ I n2S3 异质结能带在K 和K′ 附近放大图 (a),(c)没有考虑自旋轨道耦合;(b),(d)考虑自旋轨道耦合,红色虚线对应贝利曲率Fig.4.Enlarged band structure of Silicene/ I n2S3 heterostructure around K and K′: (a),(c) Calculations without spin orbit coupling;(b),(d) with spin orbit coupling,the red dotted line is the Berry curvature.

方程(2)只需要对K和K′点能隙以下能带进行求和,而方程(3)中的求和涉及所有能带,频率ωn=En/ℏ,vx(y)是速度算符.如果贝利曲率Ω(k)在整个布里渊区积分数值不为零,系统就具有量子化霍尔电导,对应拓扑非平庸状态.在硅烯/In2S3异质结中,贝利曲率在整个布里渊区积分为零,但是在K和K′点附近具有非零值,CK/K′通过在布里渊区中K/K′点附近非零区域积分求解.图4(b)中红色虚线对应对K和K′点能隙以下能带积分得到的贝利曲率,明显可以看出贝利曲率在K和K′点相反,在整个布里渊区内C=0,但是在K和K’点附近分别为CK′ ≈+1 和CK ≈-1,所以能谷CV=CK -CK′=-2,对应量子化能谷霍尔效应效应.图4(d)中贝利曲率在K和K′点也具有相反符号,仍然具有能谷自由度,只是费米能级穿过价带使体系具有金属性质.自旋轨道耦合计算表明,自发极化翻转可以调控硅烯/ I n2S3异质结在能谷霍尔态和金属态之间转变,为硅烯在能谷电子学方面的应用指明方向.

为了更直观地了解硅烯/ I n2S3异质结中自发极化电场及其翻转对异质结性质的影响,图5 给出了垂直于异质结平面方向的局域势函数的平均值.In2S3垂直方向铁电极化源于单层正中间的S 原子在垂直方向破坏了中心反演对称性,这就会导致材料两端具有不同的功函数.图5(a)中下表面功函数高于上表面,沿极化方向势能平均值降低,与自发极化向上情况一致.此时硅烯与 I n2S3间距较大,自发极化电场与衬底共同作用在K和K′点打开能隙并诱导出能谷霍尔效应状态；图5(b)中下表面功函数低于上表面,对应自发极化向下.此时硅烯与In2S3间距变小,虽然在K和K′点仍然打开能隙并且具有能谷自由度,但是界面之间的电荷转移使费米能级进入价带,体系具有金属性质.

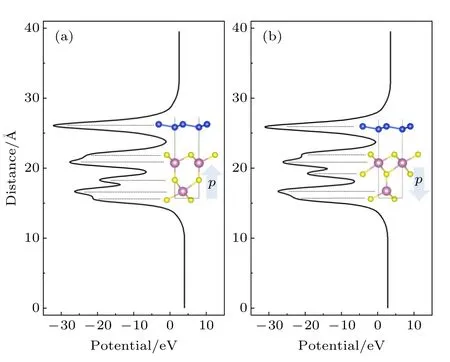
图5 硅烯/ I n2S3 异质结垂直于界面方向局域势函数的平均值Fig.5.Plane-averaged local potential of silicene/ I n2S3 heterostructure.

4 结论

通过第一性原理计算发现,单层 I n2S3的铁电极化为1.26 µ C·cm-2,其与硅烯构成的异质结中AB堆垛能量最低,I n2S3自发铁电极化的翻转会引起层间距的显著变化,自发极化方向向上时,异质结层间距较大,为3.93 Å,由于极化电场和衬底作用破坏了AB子格子对称性,在布里渊区K和K′点产生1.8 meV 能隙,费米能级在能隙之中,并且K和K′点贝利曲率符号相反,可以实现量子化的能谷霍尔效应. I n2S3自发铁电极化方向向下时,层间距变小为3.62 Å,相比极化向上时异质结之间出现0.04e的电荷转移,K和K′点能隙均为30.8 meV,但贝利曲率仍然相反,而且费米能级穿过价带具有金属性.本文的结果表明在二维铁电材料与硅烯构成的异质结中,不但可以引入能谷自由度,还可以实现二维铁电材料极化翻转对异质结电子性质的调控,为硅烯在未来能谷电子学器件中的应用提供了参考.